Find the remainder of $(f(x)=x^4+5x^3+3x^2-7x+10$ for each of the following binomials.

$$
color{#4257b2}text{(I)} (x-2)
$$

$$
f(x)=(x-2) text{quotient + remainder}
$$

$$
f(2)=0+text{remainder} f(2)=text{remainder}
$$

$$
f(2)=(2)^4+5(2)^3+3(2)^2-7(2)+10
$$

$$
f(2)=16+40+12-14+10 f(2)=64
$$

$$
text{Remainder is} 64
$$

$$
color{#4257b2}text{((II)} (x+4)
$$

$$
f(x)=(x+4) text{quotient + remainder}
$$

$$
f(-4)=0+text{remainder} f(-4)=text{remainder}
$$

$$
f(-4)=(-4)^4+5(-4)^3+3(-4)^2-7(-4)+10
$$

$$
f(-4)=256-320+48+28+10 f(2)=22
$$

$$
text{Remainder is} 22
$$

$$
color{#4257b2}text{(III)} (x-1)
$$

$$
f(x)=(x-1) text{quotient + remainder}
$$

$$
f(1)=0+text{remainder} f(1)=text{remainder}
$$

$$
f(1)=(1)^4+5(1)^3+3(1)^2-7(1)+10
$$

$$
f(1)=1+5+3-7+10 f(2)=12
$$

$$
text{Remainder is} 12
$$

$$
text{color{Brown}(I) $64$ (II) $22$ (III) $12$}
$$

Select which of the function is divisible by $x-1$

To know which function, should substitute value of $x=1$ for each one as follows:

$$
text{(a)} f(x)=x^4-15x^3+2x^2+12x-10
$$

$$
f(1)=1-15+2+12-10=-10 f(1)ne0
$$

This function is not divisible by $x-1$

$$
text{(b)} f(x)=5x^3-4x^2+3x-4
$$

$$
f(1)=5-4+3-4=1-1=0 f(1)=0
$$

This function is divisible by $x-1$

$$
text{(c)} f(x)=x^4-7x^3+2x^2+9x
$$

$$
f(1)=1-7+2+9=5 f(1)ne0
$$

This function is not divisible by $x-1$

$$
text{(d)} f(x)=x^3-1
$$

$$
f(1)=1-1=05 f(1)=0
$$

This function is divisible by $x-1$

The correct answer are (b, d)

$$
text{color{Brown}The correct answer is (b, d)}
$$

Factor the following function :

$$
f(x)=x^3+2x^2-5x-6
$$

Determine GCF as follows:

$$
f(x)=(x+3)(x^2-x-2)
$$

$$
f(x)=(x+3)(x-2)(x+1)
$$

$$
text{color{Brown} $f(x)=(x+3)(x-2)(x+1)$}
$$

State the reminder for the following expression with divisor $(x+2)$

$$
color{#4257b2}text{(a)} f(x)=x^2+7x+9
$$

$$
f(x)=(x+2) text{quotient + remainder}
$$

$$
f(-2)=0+text{remainder} f(-2)=text{remainder}
$$

$$
f(-2)=(-2)^2+7(-2)+9
$$

$$
f(-2)=4-14+9 f(-2)=-1
$$

$$
text{Remainder is} -1
$$

$$
color{#4257b2}text{(b)} f(x)=6x^3+19x^2+11x-11
$$

$$
f(x)=(x+2) text{quotient + remainder}
$$

$$
f(-2)=0+text{remainder} f(-2)=text{remainder}
$$

$$
f(-2)=6(-2)^3+19(-2)^2+11(-2)-11
$$

$$
f(-2)=-48+76-22-11 f(-2)=-5
$$

$$
text{Remainder is} -5
$$

$$
color{#4257b2}text{(c)} f(x)=x^4-5x^2+4
$$

$$
f(x)=(x+2) text{quotient + remainder}
$$

$$
f(-2)=0+text{remainder} f(-2)=text{remainder}
$$

$$
f(-2)=(-2)^4-5(-2)^2+4
$$

$$
f(-2)=16-20+4 f(-2)=0
$$

$$
text{Remainder is} 0
$$

$$
color{#4257b2}text{(d)} f(x)=x^4-2x^3-11x^2+10x-2
$$

$$
f(x)=(x+2) text{quotient + remainder}
$$

$$
f(-2)=0+text{remainder} f(-2)=text{remainder}
$$

$$
f(-2)=(-2)^4-2(-2)^3-11(-2)^2+10(-2)-2
$$

$$
f(-2)=16+16-44-20-2 f(-2)=34
$$

$$
text{Remainder is} 34
$$

$$
color{#4257b2}text{(e)} f(x)=x^3+3x^2-10x+6
$$

$$
f(x)=(x+2) text{quotient + remainder}
$$

$$
f(-2)=0+text{remainder} f(-2)=text{remainder}
$$

$$
f(-2)=(-2)^3+3(-2)^2-10(-2)+6
$$

$$
f(-2)=-8+12+20+6 f(-2)=30
$$

$$
text{Remainder is} 30
$$

$$
color{#4257b2}text{(f)} f(x)=4x^4+12x^3-13x^2-33x+18
$$

$$
f(x)=(x+2) text{quotient + remainder}
$$

$$
f(-2)=0+text{remainder} f(-2)=text{remainder}
$$

$$
f(-2)=4(-2)^4+12(-2)^3-13(-2)^2-33(-2)+18
$$

$$
f(-2)=64-96-52+66+18 f(-2)=0
$$

$$
text{Remainder is} 0
$$

$$
text{color{#4257b2}(a) $-1$ (b) $-5$ (c) $0$
\ \
(d) $34$ (e) $30$ (f) $0$}
$$

Decide if $2x-5$ is a factor for each of the following expression or not .

$$
color{#4257b2}text{(a)} 2x^3-5x^2-2x+5
$$

$(2x-5)$ is the factor, so use $left(x=dfrac{5}{2}right)$ to divide the equation as follows:

$$
begin{align*}
dfrac{5}{2} | &=2 -5 -2 5
\ \
&= 5 0 -5
\ \
&=2 0 -2 0
end{align*}
$$

$$
2x^3-5x^2-2x+5=(2x-5)(2x^2-2)
$$

$$
2x^3-5x^2-2x+5=2(2x-5)(x^2-1)
$$

The term of $2x-5$ is a factor of the expression.

$$
color{#4257b2}text{(b)} 3x^3+2x^2-3x-2
$$

$(2x-5)$ is the factor, so use $left(x=dfrac{5}{2}right)$ to divide the equation as follows:

$$
begin{align*}
dfrac{5}{2} | &=3 2 -3 -2
\ \
&= dfrac{15}{2} dfrac{95}{4} dfrac{415}{8}
\ \
&=3 dfrac{19}{2} dfrac{83}{4} dfrac{399}{8}
end{align*}
$$

The term of $2x-5$ is not a factor of the expression.

$$
color{#4257b2}text{(c)} 2x^4-7x^3-13x^2+63x-45
$$

$(2x-5)$ is the factor, so use $left(x=dfrac{5}{2}right)$ to divide the equation as follows:

$$
begin{align*}
dfrac{5}{2} | &=2 -7 -13 63 -45
\ \
&= 5 -5 -45 45
\ \
&=2 -2 -18 18 0
end{align*}
$$

The term of $2x-5$ is a factor of the expression.

$$
color{#4257b2}text{(d)} 6x^4+x^3-7x^2-x+1
$$

$(2x-5)$ is the factor, so use $left(x=dfrac{5}{2}right)$ to divide the equation as follows:

$$
begin{align*}
dfrac{5}{2} | &=6 1 -7 -1 1
\ \
&= 15 40 dfrac{165}{2} dfrac{815}{4}
\ \
&=6 16 33 dfrac{163}{2} dfrac{819}{4}
end{align*}
$$

The term of $2x-5$ is not a factor of the expression.

$$
text{color{Brown}(a) The term is a factor of the expression.
\ \
(b) The term is not a factor of the expression.
\ \
(c) The term is a factor of the expression.
\ \
(d) The term is not a factor of the expression.}
$$

Factor the following expressions

$$
color{#4257b2}text{(a)} x^3-3x^2-10x+24
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=1-3-10+24 f(1)=12
$$

$$
f(2)=8-12-20+24 f(2)=0
$$

$(x-2)$ is the factor, so use $(x=2)$ to divide the equation as follows:

$$
begin{align*}
2| &=1 -3 -10 24
\ \
&= 2 -2 -24
\ \
&=1 -1 -12 0
end{align*}
$$

$$
x^3-3x^2-10x+24=(x-2)(x^2-x-12)
$$

$$
x^3+9x^2+8x-60=(x-2)(x+3)(x-4)
$$

$$
color{#4257b2}text{(b)} 4x^3+12x^2-x-15
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=4+12-1-15 f(1)=0
$$

$(x-1)$ is the factor, so use $(x=1)$ to divide the equation as follows:

$$
begin{align*}
1| &=4 12 -1 -15
\ \
&= 4 16 15
\ \
&=4 16 15 0
end{align*}
$$

$$
4x^3+12x^2-x-15=(x-1)(x^2+16x+15)
$$

$$
x^3+9x^2+8x-60=(x-1)(x+15)(x+1)
$$

$$
color{#4257b2}text{(c)} x^4+8x^3+4x^2-48x
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=1+8+4-48 f(1)=-35
$$

$$
f(2)=16+64+16-96 f(2)=0
$$

$(x-2)$ is the factor, so use $(x=2)$ to divide the equation as follows:

$$
begin{align*}
2| &=1 8 4 -48
\ \
&= 2 20 48
\ \
&=1 10 24 0
end{align*}
$$

$$
x^4+8x^3+4x^2-48x=(x-2)(x^3+10x^2+24x)
$$

$$
x^3+9x^2+8x-60=x(x-2)(x^2+10x+24)
$$

$$
x^3+9x^2+8x-60=x(x-2)(x+6)(x+4)
$$

$$
color{#4257b2}text{(d)} 4x^4+7x^3-80x^2-21x+270
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=4+7-80-21+270 f(1)=180
$$

$$
f(3)=324+489-720-63+270 f(3)=0
$$

$(x-3)$ is the factor, so use $(x=3)$ to divide the equation as follows:

$$
begin{align*}
3| &=4 7 -80 -21 270
\ \
&= 12 57 -69 -270
\ \
&=4 19 -23 -90 0
end{align*}
$$

$$
4x^4+7x^3-80x^2-21x+270=(x-3)(4x^3+19x^2-23x-90)
$$

$$
4x^4+7x^3-80x^2-21x+270=(x-3)(x^2-4)(x+5)
$$

$$
x^3+9x^2+8x-60=(x-3)(x-2)(x+2)(x+5)
$$

$$
color{#4257b2}text{(e)} x^5-5x^4-7x^3+29x^2+30x
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=1-5-7+29+30 f(1)=48
$$

$$
f(-1)=-1-5+7+29-30 f(-1)=0
$$

$(x+1)$ is the factor, so use $(x=-1)$ to divide the equation as follows:

$$
begin{align*}
-1| &=1 -5 -7 29 30
\ \
&= -1 6 1 -30
\ \
&=1 -6 -1 30 0
end{align*}
$$

$$
x^5-5x^4-7x^3+29x^2+30x=(x+1)(x^4-6x^3-x^2+30x)
$$

$$
x^5-5x^4-7x^3+29x^2+30x=x(x+1)(x+2)(x-3)(x-5)
$$

$$
color{#4257b2}text{(f)} x^4+2x^3-23x^2-24x+144
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=1+2-23-24+144 f(1)=100
$$

$$
f(3)=81+54-207-72+144 f(3)=0
$$

$(x-3)$ is the factor, so use $(x=3)$ to divide the equation as follows:

$$
begin{align*}
3| &=1 2 -23 -24 144
\ \
&= 3 15 -24 -144
\ \
&=1 5 -8 -48 0
end{align*}
$$

$$
x^4+2x^3-23x^2-24x+144=(x-3)(x^3+5x^2-8x-48)
$$

$$
x^4+2x^3-23x^2-24x+144=(x-3)^2(x+4)^2
$$

$$
x^4+2x^3-23x^2-24x+144=(x-3)(x-3)(x+4)(x+4)
$$

$$
text{color{Brown} (a) $(x-2)(x+3)(x-4)$ (b) $(x-1)(x+15)(x+1)$
\ \
(c) $x(x-2)(x+6)(x+4)$ (d) $(x-3)(x-2)(x+2)(x+5)$
\ \
(e) $(x-3)(x-2)(x+2)(x+5)$ (f) $(x-3)(x-3)(x+4)(x+4)$}
$$

Factor the following expressions

$$
color{#4257b2}text{(a)} x^3+9x^2+8x-60
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=1+9+8-60 f(1)=-42
$$

$$
f(2)=8+36+16-60 f(2)=0
$$

$(x-2)$ is the factor, so use $(x=2)$ to divide the equation as follows:

$$
begin{align*}
2| &=1 9 8 -60
\ \
&= 2 22 60
\ \
&=1 11 30 0
end{align*}
$$

$$
x^3+9x^2+8x-60=(x-2)(x^2+11x+30)
$$

$$
x^3+9x^2+8x-60=(x-2)(x+5)(x+6)
$$

$$
color{#4257b2}text{(b)} x^3-7x-6
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=1-7-6 f(1)=-12
$$

$$
f(-1)=-1+7-6 f(-1)=0
$$

$(x+1)$ is the factor, so use $(x=-1)$ to divide the equation as follows:

$$
begin{align*}
-1| &=1 0 -7 -6
\ \
&= -1 1 6
\ \
&=1 -1 -6 0
end{align*}
$$

$$
x^3-7x-6=(x+1)(x^2-x-6)
$$

$$
x^3-7x-6=(x+1)(x+2)(x-3)
$$

$$
color{#4257b2}text{(c)} x^4-5x^2+4
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=1-5+4 f(1)=0
$$

$(x-1)$ is the factor, so use $(x=1)$ to divide the equation as follows:

$$
begin{align*}
1| &=1 0 -5 4
\ \
&= 1 1 -4
\ \
&=1 1 -4 0
end{align*}
$$

$$
x^4-5x^2+4=(x-1)(x^3+x^2-4)
$$

$$
x^4-5x^2+4=(x-1) x^2(x+1)cdot-4
$$

$$
x^4-5x^2+4=(x-1)(x+1)(x^2-4)
$$

$$
x^4-5x^2+4=(x^2-1)(x^2-4)
$$

$$
color{#4257b2}text{(d)} x^4+3x^3-38x^2+24x+64
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=1+3-38+24+64 f(1)=54
$$

$$
f(2)=16+24-152+48+64 f(1)=0
$$

$(x-2)$ is the factor, so use $(x=2)$ to divide the equation as follows:

$$
begin{align*}
2| &=1 3 -38 24 64
\ \
&= 2 10 -56 -64
\ \
&=1 5 -28 -32 0
end{align*}
$$

$$
x^4+3x^3-38x^2+24x+64=(x-2)(x^3+5x^2-28x-32)
$$

$$
x^4+3x^3-38x^2+24x+64=(x-2)(x-4)(x+1)(x+8)
$$

$$
color{#4257b2}text{(e)} x^3-x^2+x-1
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=1-1+1-1 f(1)=0
$$

$(x-1)$ is the factor, so use $(x=1)$ to divide the equation as follows:

$$
begin{align*}
1| &=1 -1 1 -1
\ \
&= 1 0 1
\ \
&=1 0 1 0
end{align*}
$$

$$
x^3-x^2+x-1=(x-1)(x^2+1)
$$

$$
color{#4257b2}text{(f)} x^5-x^4+2x^3-2x^2+x-1
$$

Use the factor theorem to factor the cubic function as follows:

$$
f(1)=1-1+2-2+1-1 f(1)=0
$$

$(x-1)$ is the factor, so use $(x=1)$ to divide the equation as follows:

$$
begin{align*}
1| &=1 -1 2 -2 1 -1
\ \
&= 1 0 2 0 1
\ \
&=1 0 2 0 1 0
end{align*}
$$

$$
x^5-x^4+2x^3-2x^2+x-1=(x-1)(x^4+2x^2+1)
$$

$$
x^5-x^4+2x^3-2x^2+x-1=(x-1)x^2(x^2+2)+1
$$

$$
x^5-x^4+2x^3-2x^2+x-1=(x-1)(x^2+1)(x^2+2)
$$

$$
text{color{Brown}(a) $(x-2)(x+5)(x+6)$ (b) $(x+1)(x+2)(x-3)$
\ \
(c) $(x^2-1)(x^2-4)$ (d) $(x-2)(x-4)(x+1)(x+8)$
\ \
(e) $(x-1)(x^2+1)$ (f) $(x-1)(x^2+1)(x^2+2)$}
$$

(a) $x^3+9x^2+8x-60$

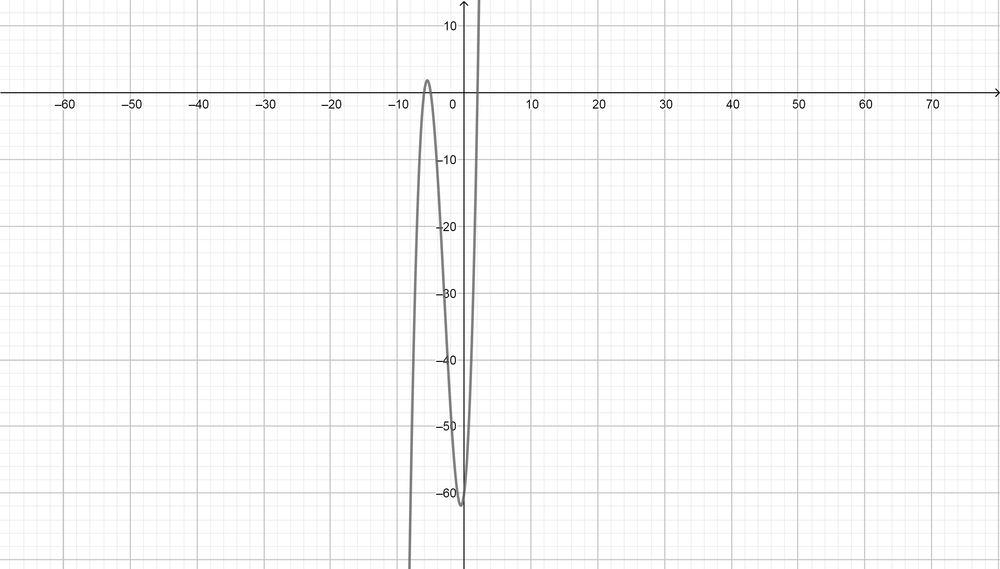
$$
(x-2)(x+5)(x+6)
$$

(b) $x^3-7x-6$

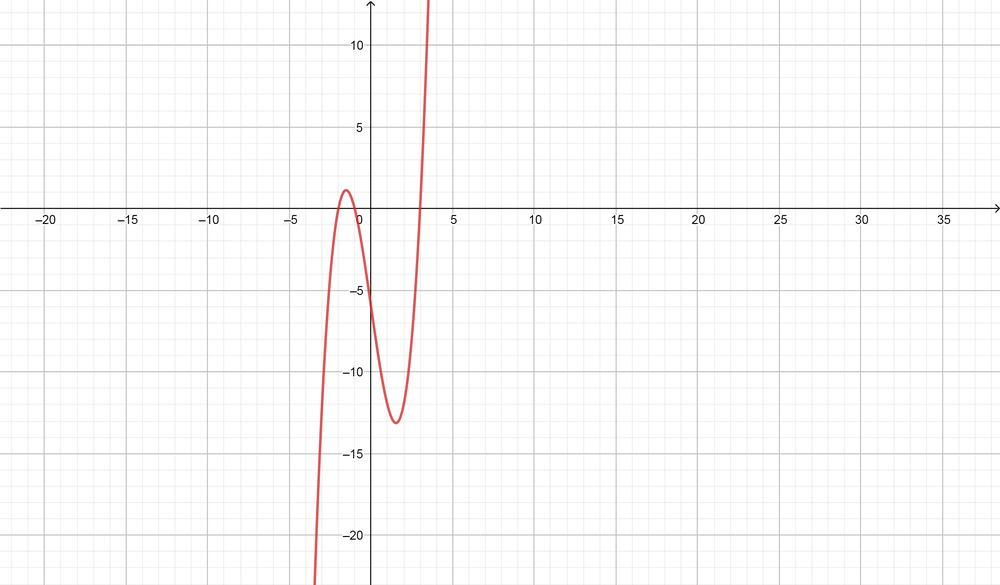
$$
(x+1)(x+2)(x-3)
$$

(c) $x^4-5x^2+4$

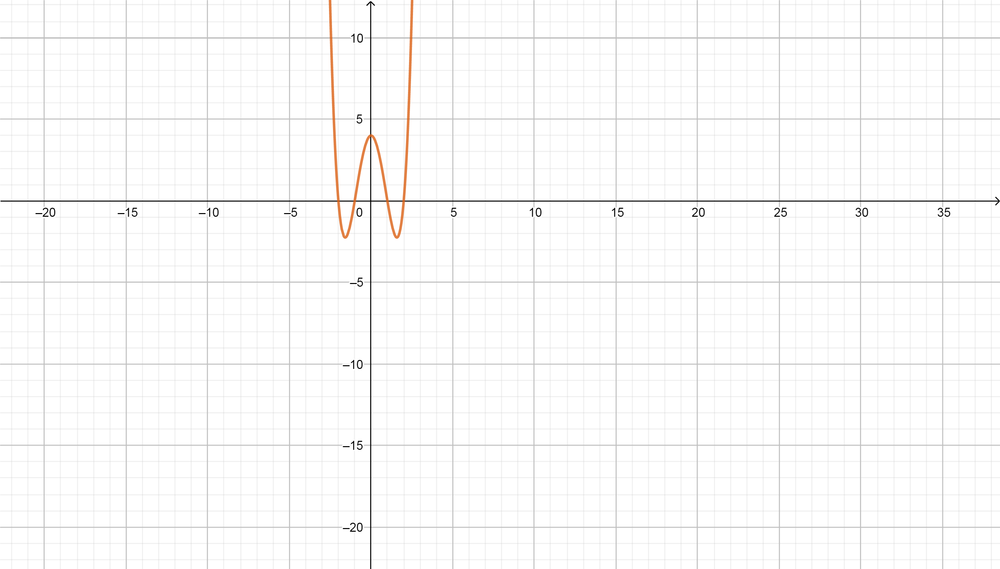
$$
(x^2-2)(x^2-4)
$$

(d) $x^4+3x^3-38x^2+24x+64$

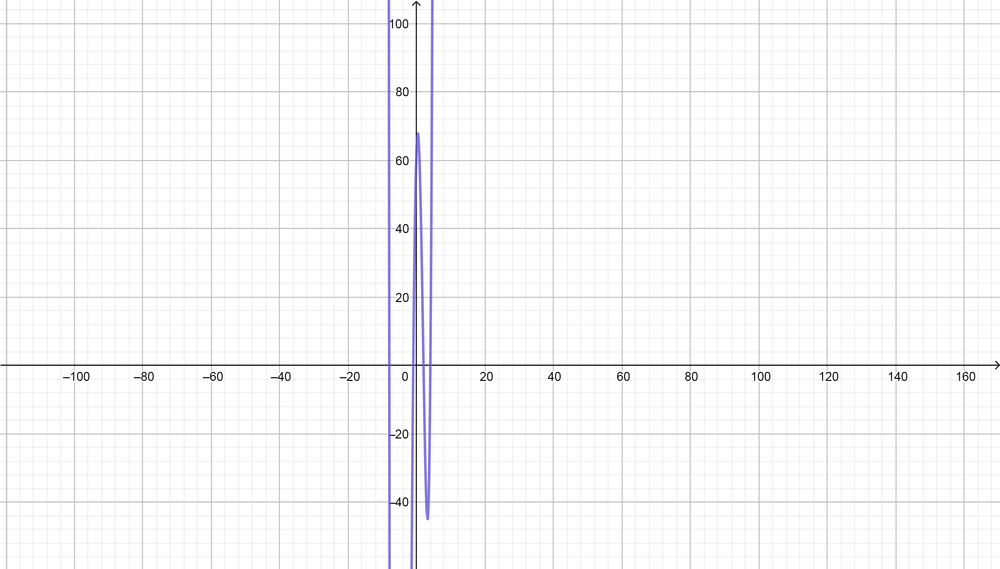
$$
(x-2)(x-4)(x+1)(x+8)
$$

(e) $x^3-x^2+x-1$

$$
(x-1)(x^2+1)
$$

(f) $x^5-x^4+2x^3-2x^2+x-1$

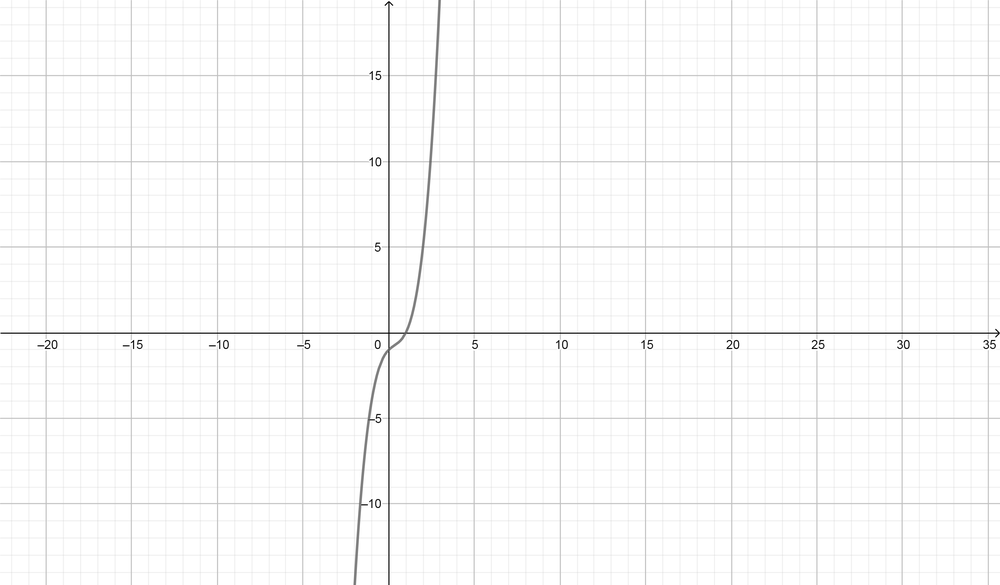
$$
(x-1)(x^2+1)(x^2+2)
$$

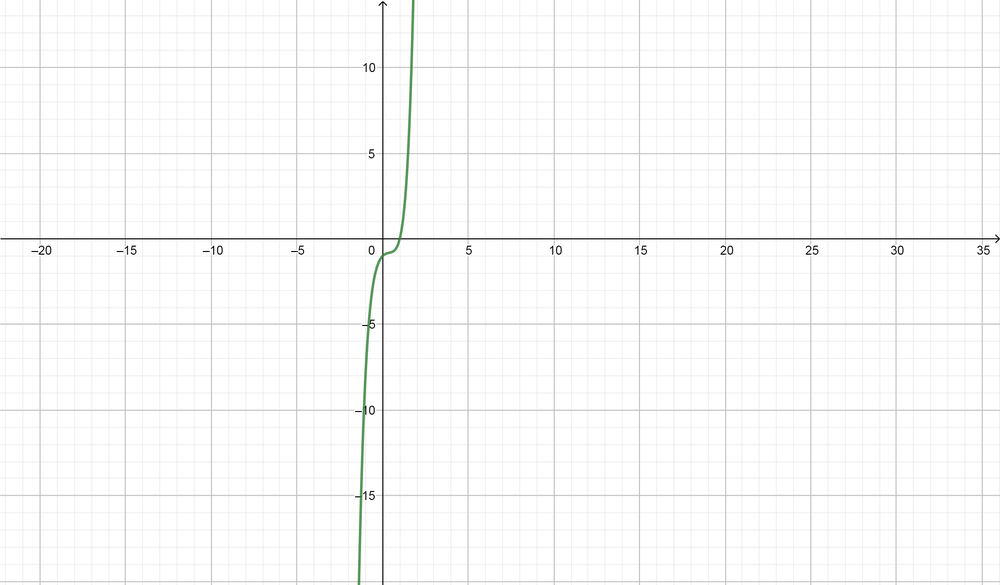
$$
text{color{Brown} See sketches}
$$

Determine the value of $k$ in the equation $(12x^3+kx^2-x-6)$ if that $(2x-1)$ is a factor.

Use zero property for the factor to get the value of $x$ as follows:

$$
2x-1=0 2x=1 x=dfrac{1}{2}
$$

Use value of $left(x=dfrac{1}{2}right)$ as follows:

$$
12left(dfrac{1}{2}right)^3+kleft(dfrac{1}{2}right)^2-left(dfrac{1}{2}right)-6=0
$$

$$
12left(dfrac{1}{8}right)+kleft(dfrac{1}{4}right)-left(dfrac{1}{2}right)-6=0
$$

$$
left(dfrac{12}{8}right)+left(dfrac{1}{4}right) k-left(dfrac{13}{2}right)=0
$$

$$
left(dfrac{1}{4}right) k=left(dfrac{13}{2}right)-left(dfrac{12}{8}right)
$$

$$
left(dfrac{1}{4}right) k=left(dfrac{104-24}{16}right)
$$

$$
left(dfrac{1}{4}right) k=left(dfrac{80}{16}right)
$$

$$
left(dfrac{1}{4}right) k=5
$$

Multiply both of sides by $4$ as follows:

$$
k=5cdot4 k=20
$$

$$
text{color{Brown}$$ k=20$$}
$$

Find $a, b$

$ax^3-x^2+2x+b$ divided by $(x-1)$ and remainder $10$

$ax^3-x^2+2x+b$ divided by $(x-2)$ and remainder $51$

For $(x-1)$ and remainder $10$

$$
f(x)=(x-1) text{quotient + remainder}
$$

Substitution the value of $x=1$ as follows:

$$
f(1)=(1-1) text{quotient}+10 f(1)=10
$$

$$
f(1)=a (1)^3-(1)^2+2(1)+b 10=a-1+2+b
$$

$$
a+b=10-1 a+b=9
$$

For $(x-2)$ and remainder $51$

$$
f(x)=(x-2) text{quotient + remainder}
$$

Substitution the value of $x=2$ as follows:

$$
f(2)=(2-2) text{quotient}+51 f(2)=51
$$

$$
f(2)=a (2)^3-(2)^2+2(2)+b 51=8a-4+4+b
$$

$$
8a+b=51
$$

Solve two equations as follows:

$$
a+b=9 8a+b=51
$$

Use elimination property as follows:

$$
(8a-a)+(b-b)=(51-9) 7a=42
$$

Divide both of sides by $7$ as follows:

$$
a=dfrac{42}{7} a=6
$$

Substitution the value of $a=6$ as follows:

$$
a+b=9 6+b=9 b=9-6 b=3
$$

$$
a=6 b=3
$$

$text{color{Brown}$$a=6 b=3$$}$

Determine the general rule to decide that:

$$
(x-a) text{is a factor of } (x^n-a^n) (x+a) text{is a factor of } (x^n+a^n)
$$

The factor of $x-a, x+a$ is a factor of a function, if and only $f(a)=0$

$$
text{color{Brown}The factor of $x-a, x+a$ is a factor of a function, if and only $f(a)=0$}
$$

Determine the values of $(a, b)$ as follows:

$$
ax^3-x^2+bx-24
$$

The factors are: $(x-2), (x+4)$

At factor $(x-2)=0 rightarrow x=2$

Substitute the value of $(x=2)$ as follows:

$$
a(2)^3-(2)^2+b(2)-24=0
$$

$$
8a-4+2b-24=0
$$

$$
8a+2b-28=0
$$

At factor $(x+4)=0 rightarrow x=-4$

Substitute the value of $(x=-4)$ as follows:

$$
a(-4)^3-(-4)^2+b(-4)-24=0
$$

$$
-64a-16-4b-24=0
$$

$$
-64a-4b-40=0
$$

Solve the two equations as follows:

Multiply the first equation by $(2)$ as follows:

$$
2 (8a-4+2b-24)=0
$$

$$
16a+4b-56=0
$$

$$
text{color{white}mmmmm nnnnnnn bbbbbbbbbbbb vvvvvvvvvvv xxxxxx ,kkkkkk ddddd}
$$

Use elimination property as follows:

$$
(-64a+16a)+(-4b+4b)+(-40-56)=0
$$

$$
-48a-96=0
$$

$$
48a=-96
$$

Divide both sides by $48$ as follows:

$$
a=-dfrac{96}{48}
$$

$$
therefore a=-2
$$

Use the first equation to get value of $b$ as follows:

$$
8a+2b-28=0
$$

$$
-16+2b-28=0
$$

$$
2b=44
$$

$$
therefore b=dfrac{44}{2}=22
$$

Now, substitute in the equation by $a$ and $b$ values, then:

$$
ax^3-x^2+bx-24=0
$$

$$
-2x^3-x^2+22x-24=0
$$

$$
text{color{white}mmmmm nnnnnnn bbbbbbbbbbbb vvvvvvvvvvv xxxxxx ,kkkkkk ddddd}
$$

$$
a=-2, b=22
$$

$$
-2x^3-x^2+22x-24=0
$$

If $ x^3+4x^2+kx-4$ the remainder from $f(x)div(x+2)$ is twice the remainder

from $f(x)div(x-2)$, find $k$

Assume the remainder is $R$

Substitute the value of $x=2$ as follows:

$$
(2)^3+4(2)^2+2k-4=R R=8+16+2k-4 R=20+2k
$$

Substitute the value of $x=-2$ as follows:

$$
(-2)^3+4(-2)^2-2k-4=2R 2R=-8+16-2k-4 2R=4-2k
$$

Adding two equation to other as follows:

$$
(2R+R)=(4+20)+(-2k+2k) 3R=24
$$

$$
R=dfrac{24}{3} R=8
$$

Substitute the value of $R=8$ as follows:

$$
R=20+2k 8=20+2k 2k=8-20
$$

$$
2k=-12 k=-dfrac{12}{2} k=-6
$$

$$
text{color{Brown} $k=-6$}
$$

Show that $(x-a)$ is a factor of $(x^4-a^4)$

Determine GCF as follows:

$$
x^4-a^4=(x-a)(x^3-a^3)
$$

Use standard form $a^3-b^3=(a-b)(a^2+ab+b^2)$

$$
x^4-a^4=(x-a)((x-a)(x^2+ax+a^2))
$$

The polynomial $(x-a)$ is a factor of $(x^4-a^4)$

$$
text{color{Brown}$$x^4-a^4=(x-a)((x-a)(x^2+ax+a^2)$$}
$$

Why the factor theorem work?

Because it can only be used when the divisor is linear that $(x-k)$ or $(ax-k)$

Make the division easier to perform.

$$
text{color{Brown}Because it can only be used when the divisor is linear that $(x-k)$ or $(ax-k)$
\ \
Make the division easier to perform.}
$$

Use theorem factor to prove that:

$x^2-x-2$ is a factor of $x^3-6x^2+3x+10$

$$
x^2-x-2=(x-2)(x+1)
$$

$(x-2)$ is the factor, so use $(x=2)$ to divide the equation as follows:

$$
begin{align*}
2| &=1 -6 3 10
\ \
&= 20 -8 -10
\ \
&=1 -4 -5 0
end{align*}
$$

$$
x^3-6x^2+3x+10=(x-2)(x^2-4x-5)
$$

$(x+1)$ is the factor, so use $(x=-1)$ to divide the equation as follows:

$$
begin{align*}
-1| &=1 -4 -5
\ \
&= -1 5
\ \
&=1 -5 0
end{align*}
$$

$$
x^3-6x^2+3x+10=(x-2)(x-1)(x-5)
$$

$$
x^3-6x^2+3x+10=x^2-x-2 (x-5)
$$

$$
text{color{Brown}$$ x^3-6x^2+3x+10=x^2-x-2 (x-5)$$}
$$

Factor theorem states that $x-a$ is a factor of polynomial $f(x)$ if and only if $f(a)=0$.

Note the signs of $a$ in this theorem and the given exercise. Since we have to prove that $x+a$ is a factor of the given polynomial, we need to check if $f(-a)=0$. This we will prove by substituting $x=-a$ in the given polynomial.

Hence, substituting $x=-a$ instead of $x$ in the given polynomial, we obtain
$$
begin{align*}
f(-a)&=(-a+a)^5+overbrace{(-a+c)^5}^{text{Factor $-1$ out}}+(a-c)^5\
&=0^5+left(-(a-c) right)^5+(a-c)^5&&text{[Note that $(-m)^5=-m^5$]}\
&=-(a-c)^5+(a-c)^5\
&=0.
end{align*}
$$
Since we’ve proven that $f(-a)=0$, by the Factor Theorem $x+a$ has to be a factor of the given polynomial $f(x)$.