
All Solutions
Page 122: Getting Started
$$
color{#4257b2}text{(a)} 2x^2(3x-11)
$$
Use distributive property as follows:
$$
2x^2(3x)-2x^2(11)
$$
$$
6x^3-22x^2
$$
$$
color{#4257b2}text{(b)} (x-4)(x+6)
$$
Use distributive property as follows:
$$
x(x+6)-4(x+6)
$$
$$
x^2+6x-4x-24
$$
Add similar tiles to group like terms as follows:
$$
x^2+(6x-4x)-24
$$
$$
x^2+2x-24
$$
color{#4257b2}text{(c)} 4x(2x-5)(3x+2)
$$
Use distributive property as follows:
$$
4x[2x(3x+2)-5(3x+2)]
$$
$$
4x[6x^2+4x-15x-10]
$$
$$
24x^3+16x^2-60x^2-40x
$$
Add similar tiles to group like terms as follows:
$$
24x^3+(16x^2-60x^2)-40x
$$
$$
24x^3-44x^2-40x
$$
$$
color{#4257b2}text{(d)} (5x-4)(x^2+7x-8)
$$
Use distributive property as follows:
$$
5x(x^2+7x-8)-4(x^2+7x-8)
$$
$$
5x^3+35x^2-40x-4x^2-28x+32
$$
Add similar tiles to group like terms as follows:
$$
5x^3+(35x^2-4x^2)+(-40x-28x)+32
$$
$$
5x^3+31x^2-68x+32
$$
text{color{Brown}(a) $6x^3-22x^2$ (b) $x^2+2x-24$
\ \
(c) $24x^3-44x^2-40x$ (d) $5x^3+31x^2-68x+32$}
$$
$$
color{#4257b2}text{(a)} x^2+3x-28
$$
Now, we need pair of number that has a $color{#4257b2}-28$ and sum of $color{#4257b2} 3$.
$$
1cdot-28=-27 text{Not true}
$$
$$
-4cdot7=3 text{True}
$$
The factor of the expression $color{#4257b2}x^2+3x-28$ can be represent as follows:
$$
(x-4)(x+7)
$$
$$
color{#4257b2}text{(b)} 2x^2-18x+28
$$
Use greatest common factor as follows:
$$
2(x^2-9x+14)
$$
Now, we need pair of number that has a $color{#4257b2}14$ and sum of $color{#4257b2} -9$.
$$
1cdot14=15 text{Not true}
$$
$$
-2cdot-7=-9 text{True}
$$
The factor of the expression $color{#4257b2}2(x^2-9x+14)$ can be represent as follows:
$$
2(x-2)(x-7)
$$
Largecolor{Brown}text{(a)} (x-4)(x+7) text{(b)} 2(x-2)(x-7)
$$
$$
color{#4257b2}text{(a)} 3x+7=x-5
$$
Isolate the variables on left side as follows:
$$
3x-x=-5-7 2x=-12
$$
Divide both of sides by $2$ to remove $2$ from the left side as follows:
$$
x=dfrac{-12}{2} x=-6
$$
$$
color{#4257b2}text{(b)} (x+3)(2x-9)=0
$$
Use zero property as follows:
$$
x+3=0 x=-3
$$
$$
2x-9=0 2x=9
$$
Divide both of sides by $2$ as follows:
$$
x=dfrac{9}{2}
$$
color{#4257b2}text{(c)} x^2+11x+24=0
$$
Now, we need pair of number that has a $color{#4257b2}24$ and sum of $color{#4257b2} 11$.
$$
1cdot24=25 text{Not true}
$$
$$
3cdot8=24 text{True}
$$
The factor of the expression $color{#4257b2}x^2+11x+24=0$ can be represent as follows:
$$
(x+3)(x+8)
$$
Use zero property as follows:
$$
x+3=0 x=-3
$$
$$
x+8=0 x=-8
$$
color{#4257b2}text{(d)} 6x^2+22x=8
$$
Use zero property as follows:
$$
6x^2+22x-8=0
$$
Use greatest common factor as follows:
$$
2(3x^2+11x-4)=0
$$
Use complete square property as follows:
$$
ac=3cdot-4 ac=-12
$$
Now, we need pair of number that has a $color{#4257b2}-12$ and sum of $color{#4257b2} 11$.
$$
3x^2+12x-x-4=0
$$
Use greatest common factor as follows:
$$
3x(x+4)-(x+4)=0 (x+4)(3x-1)
$$
Use zero property as follows:
$$
x+4=0 x=-4
$$
$$
3x-1=0 3x=1 x=dfrac{1}{3}
$$
text{color{Brown}(a) $x=-6$ (b) $x=dfrac{9}{2}$
\ \
(c) $x=-3, x=-8$ (d) $x=-4, x=dfrac{1}{3}$}
$$
a) $y=dfrac{1}{4} cdot (x-3)^{2}+9$
$$
begin{enumerate}
* vertical compression by $color{#4257b2}dfrac {1}{4}$
* horizontal translation color{#4257b2}3 color{default} units to the right
* vertical translation color{#4257b2}9 color{default} units up
end{enumerate}
$$
begin{enumerate}
item vertical compression by color{#c34632} $dfrac{1}{4}$color{default}
item vertical translation color{#c34632} 7 color{default} units down
end{enumerate}
$$
$$
begin{enumerate}
item vertical translation color{#4257b2}2 units downcolor{default}
item horizontal translation color{#4257b2}5 units to the right color{default}
item when $y=0$ then $x=4$ and $x=6$ meaning: \\
$0=k cdot 1^{2}-2 Rightarrow k=2$ \\ie. it has vertical stretch color{#4257b2}by 2color{default}
end{enumerate}
$$
begin{enumerate}
item vertical translation color{#c34632} 3 units upcolor{default}
item when $y=1$ then $x=1$ and $x=-1$: \\
$1=kcdot 1+3 Rightarrow k=-2$ \\
ie. it has vertical stretch color{#c34632} by 2 color{default}
end{enumerate}
$$
b)$y=-2cdot x^{2}+3$
$$
color{#4257b2}text{(a)} y=3(x+5)^2-4
$$
$$
y=3(x^2+10x+25)-4
$$
Use distributive property as follows:
$$
y=3x^2+30x+75-4
$$
$$
y=3x^2+30x+71
$$
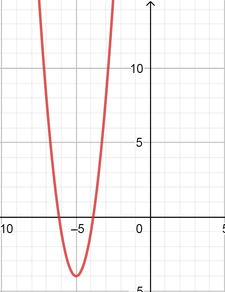
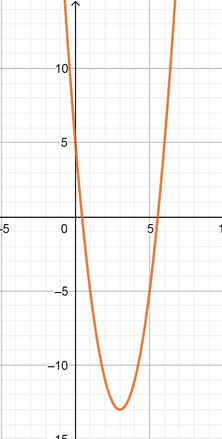
color{#4257b2}text{(b)} y=2x^2-12x+5
$$
text{color{Brown}See sketches}
$$
$$
color{#4257b2}(a) x=-2, -1, 0, 1, 2 y=56.4, 50.6, 45, 39.6, 34.4
$$
First differences as following:
$$
begin{align*}
50.6-56.4 &=-5.8 45-50.6=-5.6
\ \
39.6-45&=-5.4 34.4-39.6=-5.2
end{align*}
$$
The first differences are not constant, so check the second difference as follows:
$$
begin{align*}
-5.6-(-5.8)&=0.2 -5.4-(-5.6)=0.2
\ \
-5.2-(-5.4)&=0.2
end{align*}
$$
The second differences are constant, so the quadratic function is the best modeling for these data.
color{#4257b2}(b) x=-2, -1, 0, 1, 2 y=11, 5, 2, 7, 13
$$
First differences as following:
$$
begin{align*}
5-11&=-6 2-5=-3
\ \
7-2&=5 13-7=6
end{align*}
$$
The first differences are not constant, so check the second difference as follows:
$$
begin{align*}
-3-(-6)&=3 5-(-3)=8
\ \
6-5&=1
end{align*}
$$
The second differences are not constant, so check the ratio of $y$ values as follows:
$$
dfrac{8}{3}=2.6 dfrac{1}{8}=0.125
$$
The ratios of $y$ values are not constant, so these data are other function.
color{#4257b2}(c) x=-2, -1, 0, 1, 2 y=2, 6, 18, 54, 162
$$
First differences as following:
$$
begin{align*}
6-2&=4 18-6=12
\ \
54-18&=36 162-54=108
end{align*}
$$
The first differences are not constant, so check the second difference as follows:
$$
begin{align*}
12-4&=8 36-12=24
\ \
108-36&=72
end{align*}
$$
The second differences are not constant, so check the ratio of $y$ values as follows:
$$
dfrac{24}{8}=3 dfrac{72}{24}=3
$$
The ratios of $y$ values are equal, so the exponential function is the best modeling for these data.
color{#4257b2}(d) x=-2, -1, 0, 1, 2 y=7, 6.5, 6, 5.5, 5
$$
First differences as following:
$$
begin{align*}
6.5-7&=-0.5 6-6.5=-0.5
\ \
5.5-6&=-0.5 5-5.5=-0.5
end{align*}
$$
The first differences are not constant, so the linear function is the best modeling for these data.
text{color{Brown}(a) The quadratic function is the best modeling for these data.
\ \
(b) These data are other function.
\ \
(c) The exponential function is the best modeling for these data.
\ \
(d) The linear function is the best modeling for these data.}
$$
The intercept of the graph of the quadratic function we obtain by substituting $x=0$ in the given expression. Hence, the $y$ intercept is
$$
y=3cdot 0^2+24cdot0+36=36.
Note that $3$ is a common multiple for all three terms in the given function. Hence, taking $3$ out, we obtain
$$
f(x)=3(x^2+8x+12).
$$
Now note that the middle term $8x$ we can rewrite as $2x+6x$, then group the terms and find their common multiple, and repeat the process until we have three factors. It yields:
$$
begin{align*}
f(x)&=3(overbrace{x^2+2x}^{text{CM}=x}+overbrace{6x+12}^{text{CM}=6})\
&=3(overbrace{x(x+2)+6(x+2)}^{text{CM}=x+2})\
&=3(x+2)(x+6).
end{align*}
Note that any quadratic function of a standard form $y=ax^2+bx+c$ with coefficients $a$, $b$ and $c$ we can rewrite in a vertex form
$$
y=a(x-h)^2+k,
$$
where $h=-frac{b}{2a}$ and $k=f(h)$, which we obtain by substituting $x=h$ in the given standard form of the function.
Hence, using these formulas for the given function $y=3x^2+24+36$, where $a=3$, $b=24$ and $c=36$, we can compute
$$
h=-dfrac{b}{2a}=-dfrac{24}{2cdot3}=-4.
$$
Furthermore, substituting $x=4$ into given equation, er obtain
$$
begin{align*}
k&=f(-4)\&=3(-4)^2+24cdot(-4)+36\&=3cdot16-96+36\&=48-60\&=-12.
end{align*}$$
Hence, the vertex form of the given function is
$$
y=3(x-(-4))^2-12=3(x+4)^2-12.$$
Axis of symmetry is a vertical line about which the graph of a quadratic function is symmetrical. It goes through the vertex of parabola and divides that parabola into two mirror images. The formula of an axis of symmetry is $x=h$. Note that we’ve obtained in the previous part that $h=-4$, so the axis of symmetry of the given quadratic function is
$$
x=-4.$$
Direction of opening of a parabola depends on the coefficient $a$ from the standard form of the quadratic function $y=ax^2+bx+c$.
$$
begin{align*}
text{If} a&>0implies text{parabola opens up}.\
text{If} a&0$, we can conclude that the parabola opens up.
Zeros of quadratic function we can easily obtain from the factored form of the function, by equalizing it with zero. Hence, we have
$$
begin{align*}
3(x+2)(x+6)=0implies& x+2&=0 implies x=-2\&x+6&=0 implies x=-6.
end{align*}
Since we’ve concluded in $(5)$ that parabola opens up, the minimum value of the quadratic function we can obtain from the $y$-coordinate of the vertex of parabola. Note that from $(3)$ the vertex has coordinates $(h,k)=(-4,-12)$, thus, the minimum value of the given function will be
$$y=-12.$$
Discriminant we obtain from the standard form $y=ax^2+bx+c$ as $D=b^2-4ac$. Knowing that from the given function we have $a=3$, $b=24$ and $c=36$, we compute discriminant as follows:
$$D=24^2-4cdot3cdot36=576-432=144.$$
The parent function for any quadratic function is the function $f(x)=x^2$ with vertex at the origin of the coordinate system $(0,0)$. Coefficients $h$ and $k$ from $(3)$ Vertex form tell us how far left/right and up/down our function is translated with respect to the parent function, respectively.
– If $h0$, the graph is moved $abs{h}$ units to the right of the parent function.
– If $k0$, the graph is moved $abs{k}$ units upward of the parent function.
Since in $(3)$ we’ve obtained $h=-4$ and $k=-12$, we can conclude that the given function is translated $4$ units to the left and $12$ units downward with respect to the parent function.

*Figure 1.* A concept web for a quadratic function

