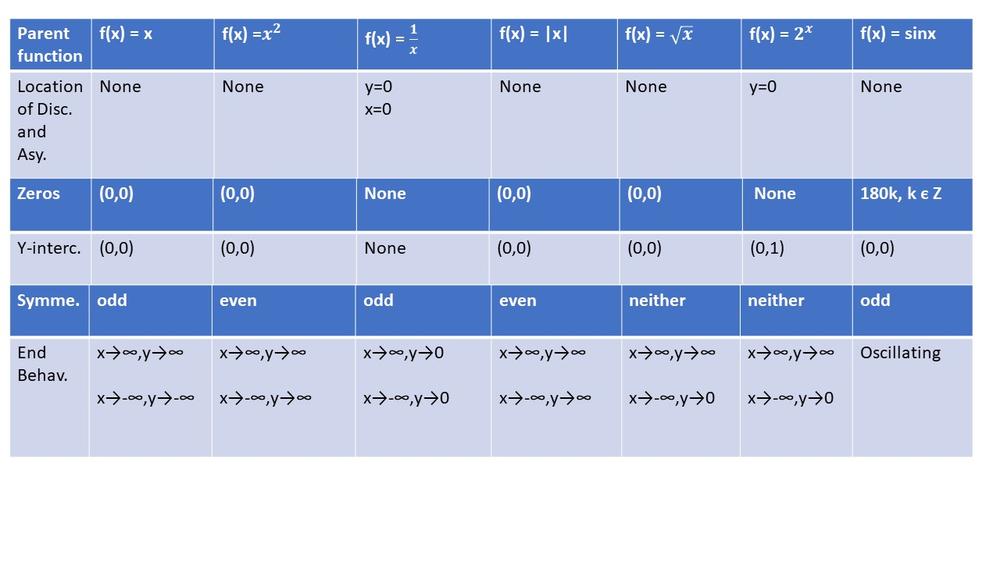
All Solutions
Page 23: Check Your Understanding
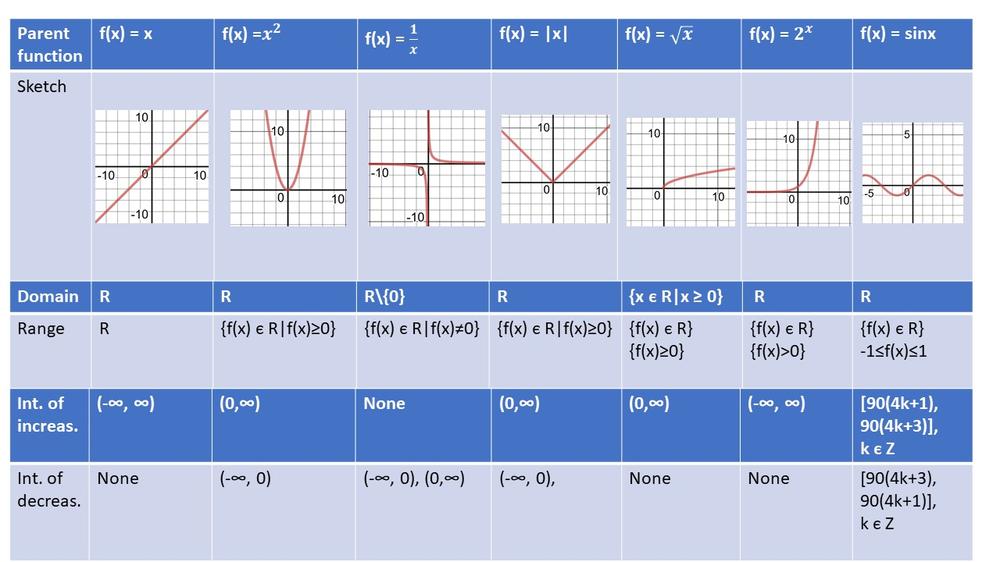
textbf{End behaviour}
$$
textbf{Domain and range}
$$
textcolor{#c34632}{ y=2+2^{x}}
$$
Here,the characteristic that these two functions have in common is that the both of them are odd functions:
$f(-x)=-dfrac{1}{x}=-f(x)$
$g(-x)=-x=-g(x)$
The characteristic that distinguishes between them is different domain:
$D(f)=R/left{0 right}$
$$
D(f)=R
$$
Here,the characteristic that these two functions have in common is that the both of them have the same domain:
$D(f)=D(g)=R$
The characteristic that distinguishes between them is different range:
$R(f)=left[-1,1 right]$
$R(g)=R$
Here,the characteristic that these two functions have in common is that the both of them have the same domain:
$D(f)=D(g)=R$
The characteristic that distinguishes between them is that function $f$ is odd function and function $g$ is even function:
$f(-x)=-x=-f(x)$
$g(-x)=(-x)^2=x^2=g(x)$
Here,the characteristic that these two functions have in common is that the both of them have the same domain:
$D(f)=D(g)=R$
The characteristic that distinguishes between them is different range:
$R(f)=left{yin R |y>0right}$
$R(g)=left{yin R |ygeq0right}$
$f(-x)=(-x)^2-4=x^2-4=f(x)$
$-f(-x)=-(x^2-4)=-f(x)$
So, the conclusion is that this function is $text{textcolor{#c34632}{even}}$ function.
The function is even if its algebraic form satisfies the relation $textbf{f(-x)=f(x)}$
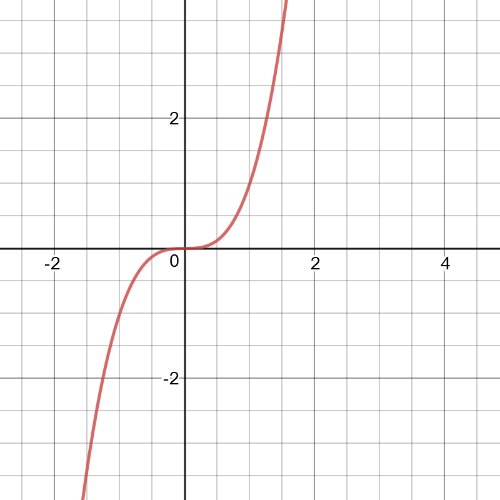
$f(-x)=sin(-x)+(-x)=-sin{x}-x=\=-(sin{x}+x)=-f(x)$
$-f(-x)=-(-(sin{x}+x))=sin{x}+x=f(x)$
So,the conclusion is that $f$ is $text{textcolor{#c34632}{odd}}$ function.
The function is odd if its algebraic form satisfies the relation $textbf{f(-x)=-f(x)}$
$$
f(-x)=-dfrac{1}{x}-(-x)=-dfrac{1}{x}+x=-(dfrac{1}{x}-x)=-f(x)
$$
$-f(-x)=-(-(dfrac{1}{x}-x))=dfrac{1}{x}-x=f(x)$
So, the conclusion is that $f$ is $text{textcolor{#c34632}{odd}}$ function.
$f(-x)=2(-x)^2+(-x)=2x^2-x$
$Rightarrow(f(-x)ne f(x) wedge f(-x)ne-f(x))$
$-f(-x)=-(2x^2-x)=-2x^2+x$
So,the conclusion is that function $f$ is $text{textcolor{#c34632}{neither}}$ function
The function is neither if its algebraic form does not satisfiy the relations $textbf{f(-x)=f(x)}$ or $textbf{f(-x)=-f(x)}$
$f(-x)=2(-x)^2-(-x)=2x^2+x$
$Rightarrow(f(-x)ne f(x) wedge f(-x)ne-f(x))$
$-f(-x)=-(2x^2+x)=-2x^2-x$
So,the conclusionis that $f$ is $text{textcolor{#c34632}{neither}}$ function.
$f(-x)=|2(-x)+3|=|-2x+3|=|-(2x-3)|=\=|2x-3|$
$-f(-x)=-|2x-3|$
So, the conclusion is that $f$ is $text{textcolor{#c34632}{neither}}$ function.
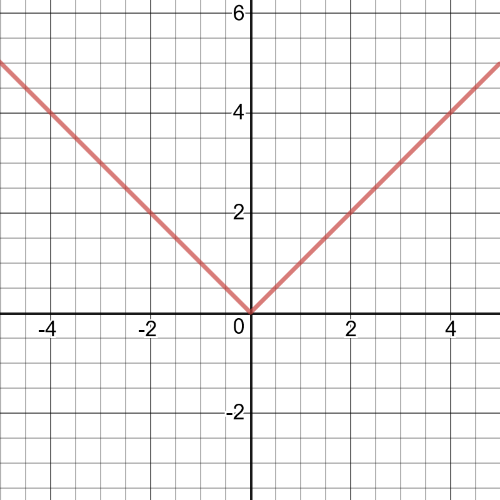
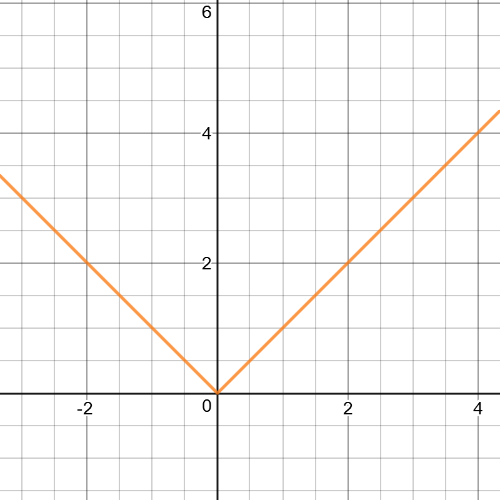
$|x|$,because it is a measure of distance from a number.
#### (b)
$sin(x)$,because the heights are periodic
#### (c)
$2^x$, because population tends to increase exponentially
#### (d)
$x$,because there is $1 on the first day, $2 on the second, $3 on the third, etc.
It might be the following function:
$f(x)=dfrac{x}{1-x}$
For real, the domain of this function is real numbers without 1, it is because of the denominator, $x-1$. In order for a function to be defined, the denominator must be different from zero, and in this case it is different from zero for $xne1$.
Also, the second condition is satisfied:
$f(0)=dfrac{0}{1-0}=0$
#### (b)
It might be the following function:
$f(x)=sin{x}$
As we could see from some of the previous examples, the graph of this function infinitely many times cuts x axis, so it has infinitely many zeros.
#### (c)
It might be the following function:
$f(x)=cos{x}$
Its graph is even, because this function is even function, and also, its graph is smooth,it has not sharps.
It might be the following function:
$y=x$
Values that take $x$, the same values are taken by $y$.
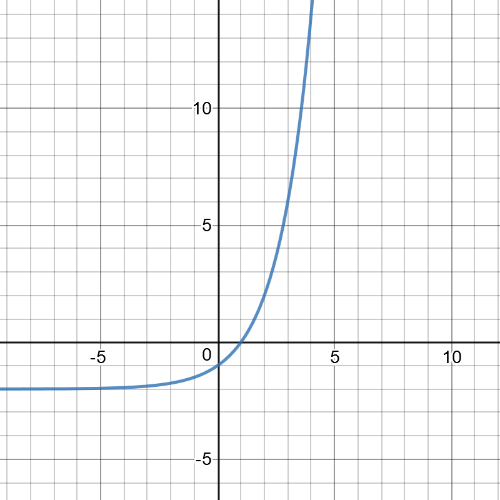
According to all the data given to us about the function, we conclude that the function satisfying all of them can be $f(x)=2^x-2$, which is proved by the following graph of this function:
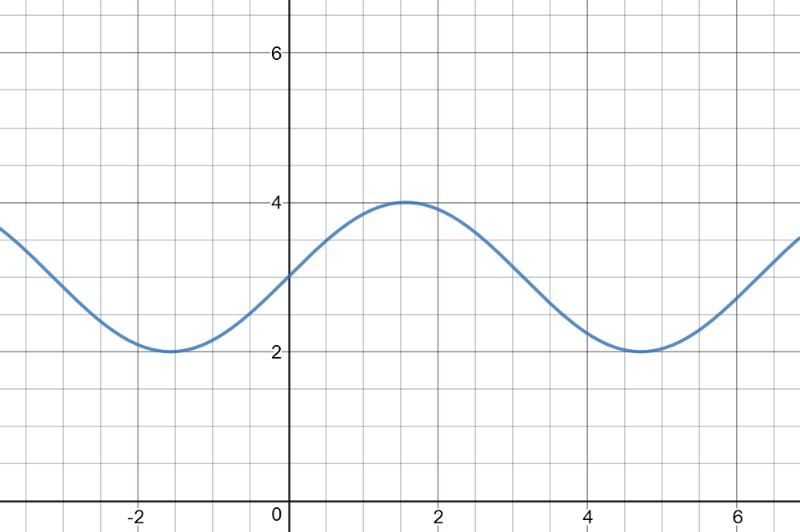
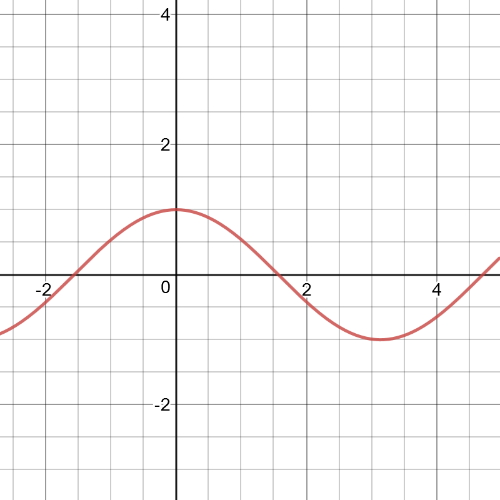
According to all the data given to us about the function, we conclude that the function satisfying all of them can be $f(x)=sin{x}+3$, which is proved by the following graph of this function:
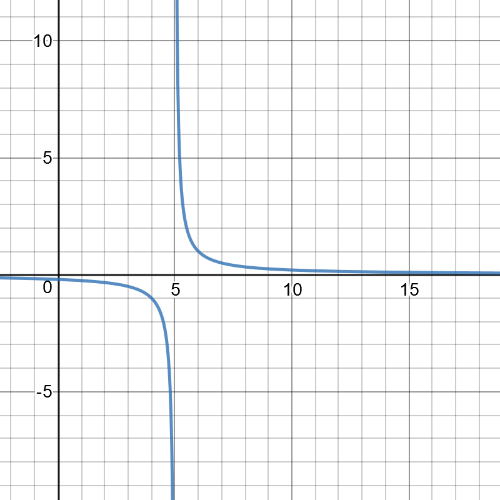
According to all the data given to us about the function, we conclude that the function satisfying all of them can be $f(x)=dfrac{1}{x-5}$, which is proved by the following graph of this function:
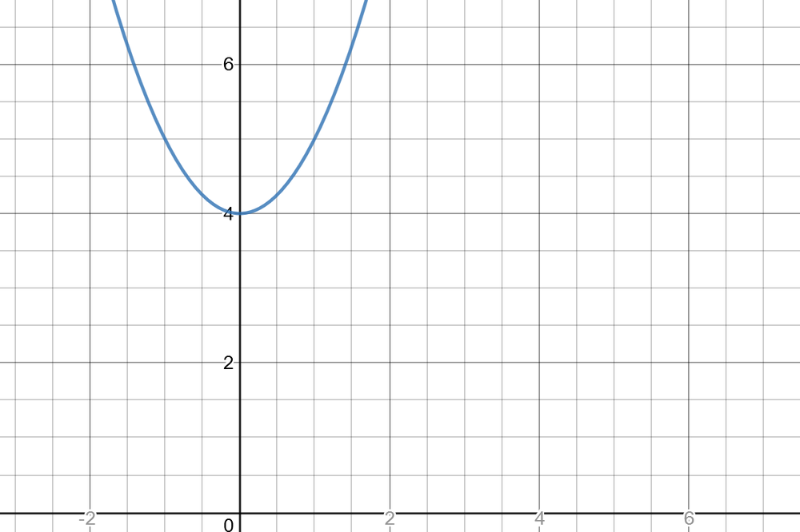
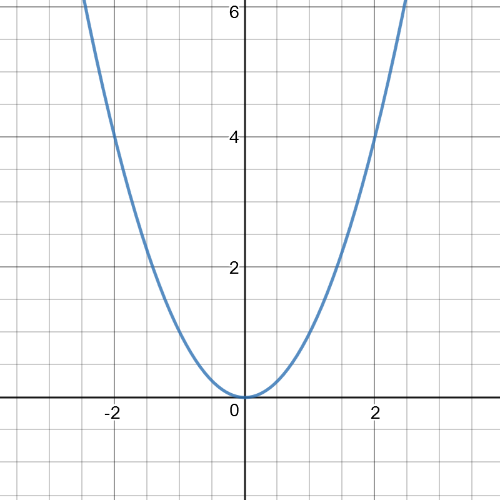
According to all the data given to us about the function, we conclude that a function satisfying all of them, and besides being a quadratic function, can be $f(x)=x^2+4$, which is also proved by the following graph of this function:
There $textbf{is not}$ only one quadratic function, that has the
characteristics given in part a). Characteristics remain the same with each change of coefficient with positive sign in front of $x^2$.
#### (d)
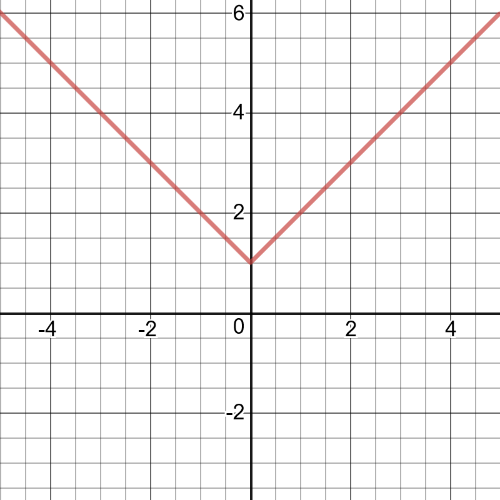
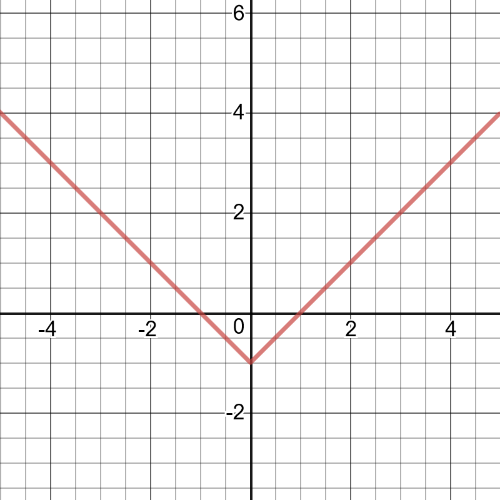
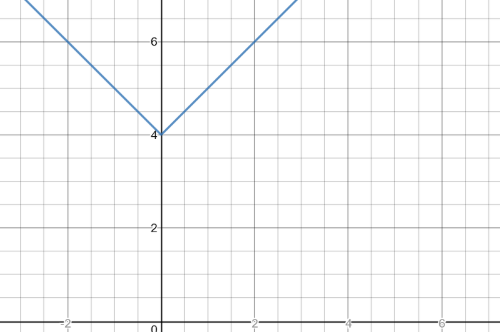
If $f$ is an absolute value function, its transformation satisfying all the conditions given in a) would be a function $f(x)=left|x right|+4$ .Analogously, as a pre-emptive function, the characteristics will not change if we change coefficients with a positive sign in front of $left|x right|$. The appearance of the absolute function that fits all of the above is found in the following graphic:
$0$ zeros: