(a) We would like to state the zeros of the functions $color{#4257b2}y=2xleft(x-1right)left(x+2right)left(x-2right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
y=2xleft(x-1right)left(x+2right)left(x-2right)
$$

$$
y=2xleft(x-1right)left(x+2right)left(x-2right)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}y$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
2xleft(x-1right)left(x+2right)left(x-2right)=0
$$

$$
2x=0, x-1=0, x+2=0 text{or} x-2=0
$$

$$
x=0, x=1, x=-2 text{or} x=2
$$

So the zeros of the function $color{#4257b2}y$ are $boxed{ x=0, x=1, x=-2 } text{or} boxed{ x=2 }$

(b) We would like to state the zeros of the functions $color{#4257b2}y=5left(2x+3right)left(4x-5right)left(x+7right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
y=5left(2x+3right)left(4x-5right)left(x+7right)
$$

$$
y=5left(2x+3right)left(4x-5right)left(x+7right)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}y$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
5left(2x+3right)left(4x-5right)left(x+7right)=0
$$

$$
2x+3=0, 4x-5=0 text{or} x+7=0
$$

$$
x=-dfrac{3}{2}, x=dfrac{5}{4} text{or} x=-7
$$

So the zeros of the function $color{#4257b2}y$ are $boxed{ x=-dfrac{3}{2}, x=dfrac{5}{4} } text{or} boxed{ x=-7 }$

(c) We would like to state the zeros of the functions $color{#4257b2}y=2left(x-3right)^{2}left(x+5right)left(x-4right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
y=2left(x-3right)^{2}left(x+5right)left(x-4right)
$$

$$
y=2left(x-3right)^{2}left(x+5right)left(x-4right)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}y$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
2left(x-3right)^{2}left(x+5right)left(x-4right)=0
$$

$$
left(x-3right)^{2}=0, x+5=0 text{or} x-4=0
$$

$$
x=3, x=-5 text{or} x=4
$$

Note that the bracket $color{#4257b2}left(x-3right)^{2}$ has two zeros but the two zeros equal $color{#4257b2}3$, so we wrote it just once.

So the zeros of the function $color{#4257b2}y$ are $boxed{ x=3, x=-5 } text{or} boxed{ x=4 }$

(d) We would like to state the zeros of the functions $color{#4257b2}y=left(x+6right)^{3}left(2x-5right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
y=left(x+6right)^{3}left(2x-5right)
$$

$$
y=left(x+6right)^{3}left(2x-5right)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}y$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
left(x+6right)^{3}left(2x-5right)=0
$$

$$
left(x+6right)^{3}=0 text{or} 2x-5=0
$$

$$
x=-6 text{or} x=dfrac{5}{2}
$$

Note that the bracket $color{#4257b2}left(x+6right)^{3}$ has three zeros but the three zeros equal $color{#4257b2}-6$, so we wrote it just once.

So the zeros of the function $color{#4257b2}y$ are $boxed{ x=-6 } text{or} boxed{ x=dfrac{5}{2} }$

(e) We would like to state the zeros of the functions $color{#4257b2}y=-5xleft(x^{2}-9right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
y=-5xleft(x^{2}-9right)
$$

$$
y=-5xleft(x^{2}-9right)=0
$$

But we note that the term $color{#4257b2}x^{2}-9$ is on the form $color{#4257b2}a^{2}-b^{2}$, so we can factor it where $color{#4257b2}a^{2}-b^{2}=left(a-bright)left(a+bright)$.

$$
-5xleft(x^{2}-9right)=0
$$

$$
-5xleft(x-3right)left(x+3right)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}y$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
-5xleft(x-3right)left(x+3right)=0
$$

$$
-5x=0, x-3=0 text{or} x+3=0
$$

$$
x=0, x=3 text{or} x=-3
$$

So the zeros of the function $color{#4257b2}y$ are $boxed{ x=0, x=3 } text{or} boxed{ x=-3 }$

(f) We would like to state the zeros of the functions $color{#4257b2}y=left(x+5right)left(x^{2}-4x-12right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
y=left(x+5right)left(x^{2}-4x-12right)
$$

$$
y=left(x+5right)left(x^{2}-4x-12right)=0
$$

But we note that the term $color{#4257b2}x^{2}-4x-12$ is a quadratic function, so we can factor it to find the zeros.

$$
left(x+5right)left(x^{2}-4x-12right)=0
$$

$$
left(x+5right)left(x-6right)left(x+2right)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}y$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
left(x+5right)left(x-6right)left(x+2right)=0
$$

$$
x+5=0, x-6=0 text{or} x+2=0
$$

$$
x=-5, x=6 text{or} x=-2
$$

So the zeros of the function $color{#4257b2}y$ are $boxed{ x=-5, x=6 } text{or} boxed{ x=-2 }$

$$
color{Brown}(a) x=0, x=1, x=-2 {color{Black}text{or}} x=2
$$

$$
color{Brown}(b) x=-dfrac{3}{2}, x=dfrac{5}{4} {color{Black}text{or}} x=-7
$$

$$
color{Brown}(c) x=3, x=-5 {color{Black}text{or}} x=4
$$

$$
color{Brown}(d) x=-6 {color{Black}text{or}} x=dfrac{5}{2}
$$

$$
color{Brown}(e) x=0, x=3 {color{Black}text{or}} x=-3
$$

$$
color{Brown}(f) x=-5, x=6 {color{Black}text{or}} x=-2
$$

(a) We would like to solve the equation $color{#4257b2}3x^{3}=27x$ by factoring. First, we can subtract $color{#4257b2}27x$ from each side to make the right side equals zero.

$$
3x^{3}=27x
$$

$$
3x^{3}-27x=0
$$

Now we note that each term of the equation contains $color{#4257b2}3x$, so we can take $color{#4257b2}3x$ as a common factor.

$$
3xleft(x^{2}-9right)=0
$$

But we note that the term $color{#4257b2}x^{2}-9$ is on the form $color{#4257b2}a^{2}-b^{2}$, so we can factor it where $color{#4257b2}a^{2}-b^{2}=left(a-bright)left(a+bright)$.

$$
3xleft(x-3right)left(x+3right)=0
$$

Now we can use the zero-factor property to solve the equations for $color{#4257b2}x$.

$$
3x=0, x-3=0 text{or} x+3=0
$$

$$
x=0, x=3 text{or} x=-3
$$

So the solutions of the equation are $boxed{ x=0, x=3 } text{or} boxed{ x=-3 }$

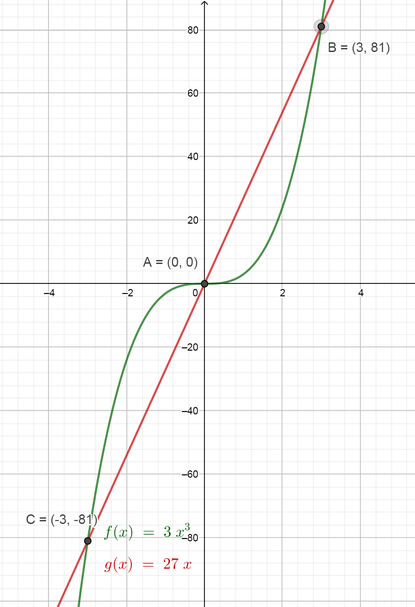
Now we can verify our solutions using the graphing technology by graphing the function on the left side $color{#4257b2}3x^{3}$ and also graph the function on the right side $color{#4257b2}27x$ on the same plane and then find the points where the two graphs will intersect and find the values of $color{#4257b2}x$ at these points. Note that the values of $color{#4257b2}x$ at the intersect points are the solutions of the equation.

We note from the graph that the two functions intersect at the points $color{#4257b2}A, B$ and $color{#4257b2}C$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}0, 3$ and $color{#4257b2}-3$, so we verified our solutions analytically using the graphing technology.

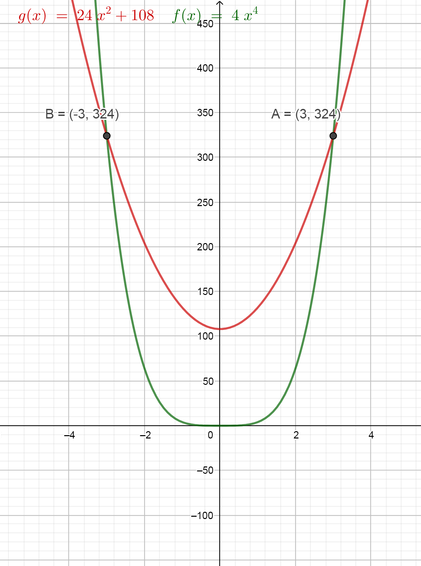
(b) We would like to solve the equation $color{#4257b2}4x^{4}=24x^{2}+108$ by factoring. First, we can subtract $color{#4257b2}24x^{2}+108$ from each side to make the right side equals zero.

$$
4x^{4}=24x^{2}+108
$$

$$
4x^{4}-24x^{2}-108=0
$$

Now we can divide the two sides by $4$.

$$
x^{4}-6x^{2}-27=0
$$

Now we have an equation of the fourth degree, so we can factor it to two multiplied functions from the second degree.

$$
left(x^{2}-9right)left(x^{2}+3right)=0
$$

Now we can use the zero-factor property to solve the equations for $color{#4257b2}x$.

$$
x^{2}-9=0 text{or} x^{2}+3=0
$$

$$
x^{2}-9=0 text{or} x^{2}=-3
$$

But we know that the equation $color{#4257b2}x^{2}=-3$ gives us an imaginary solutions, so the solution of $color{#4257b2}x^{2}=-3$ is refused.

$$
x^{2}-9=0
$$

Now we note that or equation $color{#4257b2}x^{2}-9$ is on the form $color{#4257b2}a^{2}-b^{2}$, so we can factor it where $color{#4257b2}a^{2}-b^{2}=left(a-bright)left(a+bright)$.

$$
x^{2}-9=0
$$

$$
left(x-3right)left(x+3right)=0
$$

$$
x=3 text{or} x=-3
$$

So the solutions of the equation are $boxed{ x=3 } text{or} boxed{ x=-3 }$

Now we can verify our solutions using the graphing technology by graphing the function on the left side $color{#4257b2}4x^{4}$ and also graph the function on the right side $color{#4257b2}4x^{2}+108$ on the same plane and then find the points where the two graphs will intersect and find the values of $color{#4257b2}x$ at these points. Note that the values of $color{#4257b2}x$ at the intersect points are the solutions of the equation.

We note from the graph that the two functions intersect at the points $color{#4257b2}A$ and $color{#4257b2}B$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}3$ and $color{#4257b2}-3$, so we verified our solutions analytically using the graphing technology.

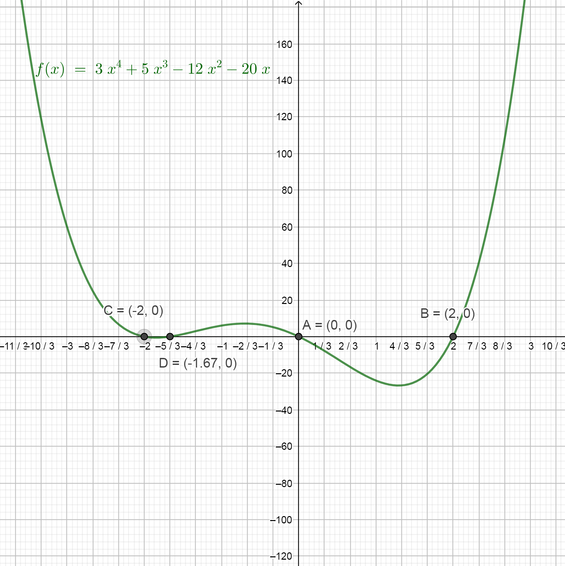
(c) We would like to solve the equation $color{#4257b2}3x^{4}+5x^{3}-12x^{2}-20x=0$ by factoring. First, we note that all terms contain $color{#4257b2}x$, so we can take $color{#4257b2}x$ as a common factor.

$$
3x^{4}+5x^{3}-12x^{2}-20x=0
$$

$$
xleft(3x^{3}+5x^{2}-12x-20right)=0
$$

Now we have a cubic equation, so we can factor it by grouping as follows:

$$
xleft(3x^{3}+5x^{2}-12x-20right)=0
$$

$$
xleft[left(3x^{3}-12xright)+left(5x^{2}-20right)right]=0
$$

$$
xleft[3xleft(x^{2}-4right)+5left(x^{2}-4right)right]=0
$$

Now we can take the term $color{#4257b2}x^{2}-4$ as a common factor.

$$
xleft(x^{2}-4right)left(3x+5right)=0
$$

But we note that the term $color{#4257b2}x^{2}-4$ is on the form $color{#4257b2}a^{2}-b^{2}$, so we can factor it where $color{#4257b2}a^{2}-b^{2}=left(a-bright)left(a+bright)$.

$$
xleft(x^{2}-4right)left(3x+5right)=0
$$

$$
xleft(x^{2}-4right)left(3x+5right)=0
$$

$$
xleft(x-2right)left(x+2right)left(3x+5right)=0
$$

Now we can use the zero-factor property to solve the equations for $color{#4257b2}x$.

$$
x=0, x-2=0, x+2=0 text{or} 3x+5=0
$$

$$
x=0, x=2, x=-2 text{or} x=-dfrac{5}{3}
$$

So the solutions of the equation are $boxed{ x=0, x=2, x=-2 } text{or} boxed{ x=-dfrac{5}{3} }$

Now we can verify our solutions using the graphing technology by graphing the function on the left side $color{#4257b2}3x^{4}+5x^{3}-12x^{2}-20x$ and then find the points where the graph will intersect the x-axis and find the values of $color{#4257b2}x$ at these points. Note that we will find the points where the graph will intersect the x-axis because the other side equal zero.

We note from the graph that the two functions intersect at the points $color{#4257b2}A, B, C$ and $color{#4257b2}D$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}0, 2, -2$ and $color{#4257b2}-dfrac{5}{3}$, so we verified our solutions analytically using the graphing technology.

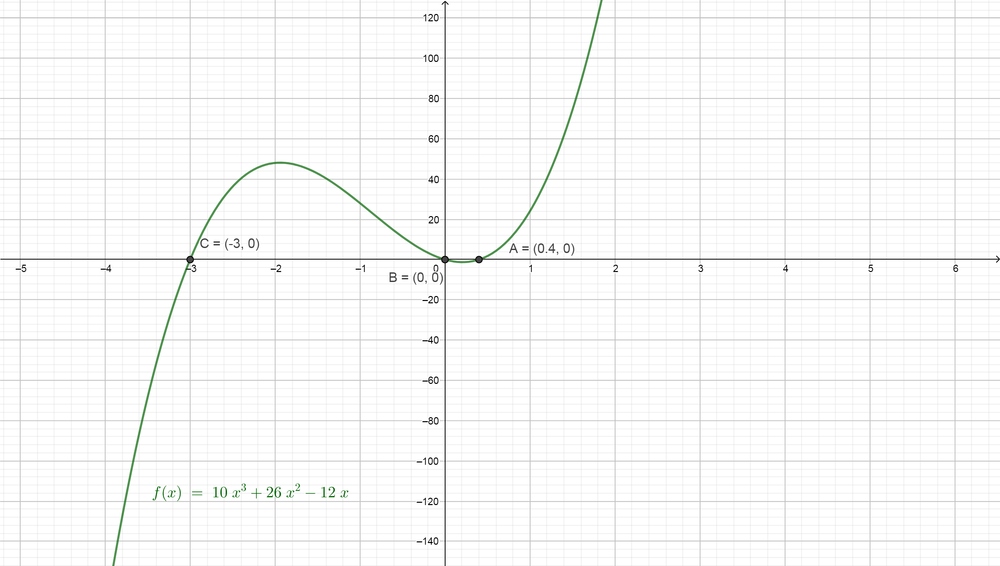
(d) We would like to solve the equation $color{#4257b2}10x^{3}+26x^{2}-12x=0$ by factoring. First, we note that all terms contain $color{#4257b2}2x$, so we can take $color{#4257b2}x$ as a common factor.

$$
10x^{3}+26x^{2}-12x=0
$$

$$
2xleft(5x^{2}+13x-6right)=0
$$

Now we have a quadratic equation, so we can factor it to find the values of $color{#4257b2}x$.

$$
2xleft(5x^{2}+13x-6right)=0
$$

$$
2xleft(x+3right)left(5x-2right)=0
$$

Now we can use the zero-factor property to solve the equations for $color{#4257b2}x$.

$$
2x=0, x+3=0 text{or} 5x-2=0
$$

$$
x=0, x=-3 text{or} x=dfrac{2}{5}
$$

So the solutions of the equation are $boxed{ x=0, x=-3 } text{or} boxed{ x=dfrac{2}{5} }$

Now we can verify our solutions using the graphing technology by graphing the function on the left side $color{#4257b2}10x^{3}+26x^{2}-12x$ and then find the points where the graph will intersect the x-axis and find the values of $color{#4257b2}x$ at these points. Note that we will find the points where the graph will intersect the x-axis because the other side equal zero.

We note from the graph that the two functions intersect at the points $color{#4257b2}A, B$ and $color{#4257b2}C$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}0.4, 0$ and $color{#4257b2}-3$, so we verified our solutions analytically using the graphing technology.

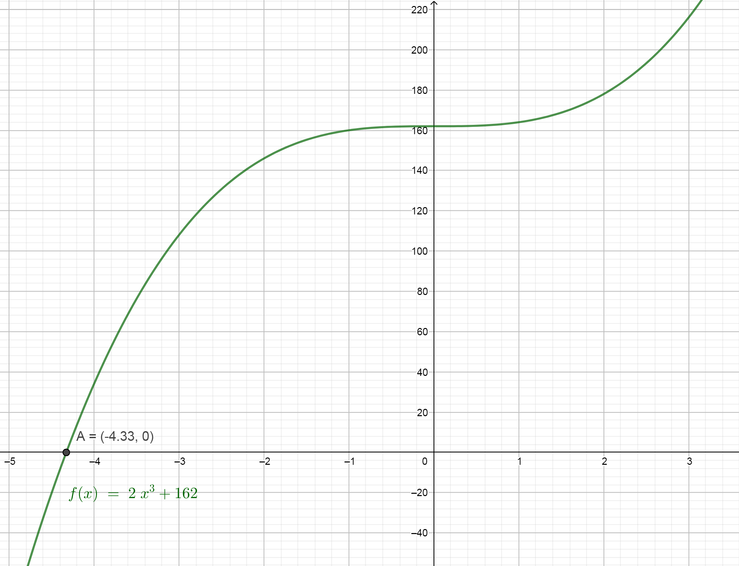
(e) We would like to solve the equation $color{#4257b2}2x^{3}+162=0$ by factoring. First, we can divide the two sides by $2$ to simplify.

$$
2x^{3}+162=0
$$

$$
x^{3}+81=0
$$

Now we have a cubic equation on the form $color{#4257b2}a^{3}+b^{3}$, so we can factor it where $color{#4257b2}a^{3}+b^{3}=left(a+bright)left(a^{2}-ab+b^{2}right)$.

$$
left(x+3sqrt[3]{3}right)left(x^{2}-3sqrt[3]{3}+9sqrt[3]{9}right)=0
$$

Now we can use the zero-factor property to solve the equations for $color{#4257b2}x$.

$$
x+3sqrt[3]{3}=0 text{or} x^{2}-3sqrt[3]{3}+9sqrt[3]{9}=0
$$

But we note that the equation $color{#4257b2}x^{2}-3sqrt[3]{3}+9sqrt[3]{9}$ has an imaginary solutions only, so the solution of $color{#4257b2}x^{2}-3sqrt[3]{3}+9sqrt[3]{9}=0$ is refused.

$$
x+3sqrt[3]{3}=0
$$

$$
x=-3sqrt[3]{3}=-4.326
$$

So the solutions of the equation are $boxed{ x=-4.326 }$

Now we can verify our solutions using the graphing technology by graphing the function on the left side $color{#4257b2}2x^{3}+162$ and then find the points where the graph will intersect the x-axis and find the values of $color{#4257b2}x$ at these points. Note that we will find the points where the graph will intersect the x-axis because the other side equal zero.

We note from the graph that the two functions intersect at the point $color{#4257b2}A$ and the value of $color{#4257b2}x$ at this point is $color{#4257b2}-4.33$, so we verified our solutions analytically using the graphing technology.

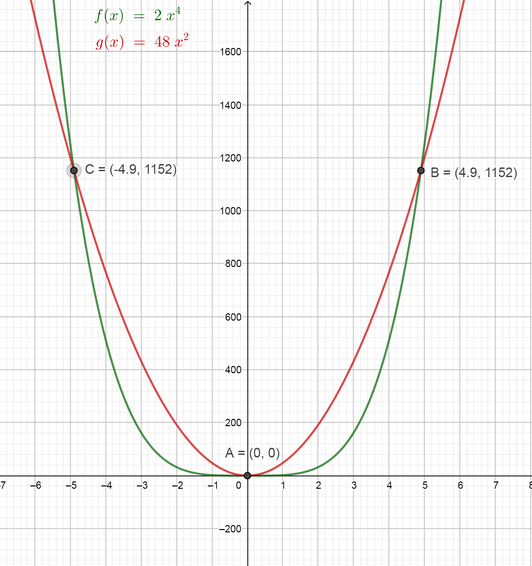
(f) We would like to solve the equation $color{#4257b2}2x^{4}=48x^{2}$ by factoring. First, we can subtract $color{#4257b2}48x^{2}$ from each side to make the right side equals zero.

$$
2x^{4}=48x^{2}
$$

$$
2x^{4}-48x^{2}=0
$$

Now we note that each term of the equation contains $color{#4257b2}2x^{2}$, so we can take $color{#4257b2}2x^{2}$ as a common factor.

$$
2x^{2}left(x^{2}-24right)=0
$$

But we note that the term $color{#4257b2}x^{2}-24$ is on the form $color{#4257b2}a^{2}-b^{2}$, so we can factor it where $color{#4257b2}a^{2}-b^{2}=left(a-bright)left(a+bright)$.

$$
2x^{2}left(x-2sqrt{6}right)left(x+2sqrt{6}right)=0
$$

Now we can use the zero-factor property to solve the equations for $color{#4257b2}x$.

$$
2x^{2}=0, x-2sqrt{6}=0 text{or} x+2sqrt{6}=0
$$

$$
x=0, x=2sqrt{6}=4.9 text{or} x=-2sqrt{6}=-4.9
$$

So the solutions of the equation are $boxed{ x=0, x=4.9 } text{or} boxed{ x=-4.9 }$

Now we can verify our solutions using the graphing technology by graphing the function on the left side $color{#4257b2}2x^{4}$ and also graph the function on the right side $color{#4257b2}48x^{2}$ on the same plane and then find the points where the two graphs will intersect and find the values of $color{#4257b2}x$ at these points. Note that the values of $color{#4257b2}x$ at the intersect points are the solutions of the equation.

We note from the graph that the two functions intersect at the points $color{#4257b2}A, B$ and $color{#4257b2}C$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}0, 4.9$ and $color{#4257b2}-4.9$, so we verified our solutions analytically using the graphing technology.

$$
color{Brown}(a) x=0, x=3 {color{Black}text{or}} x=-3
$$

$$
color{Brown}(b) x=3 {color{Black}text{or}} x=-3
$$

$$
color{Brown}(c) x=0, x=2, x=-2 {color{Black}text{or}} x=-dfrac{5}{3}
$$

$$
color{Brown}(d) x=0, x=-3 {color{Black}text{or}} x=dfrac{2}{5}
$$

$$
color{Brown}(e) x=-4.33
$$

$$
color{Brown}(f) x=0, x=4.9 {color{Black}text{or}} x=-4.9
$$

(a) Since we need to determine the zeros of the function
$color{#4257b2}y=2x^{3}-17x^{2}+23x+42$, we can use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}y=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}y=2x^{3}-17x^{2}+23x+42$, so $color{#4257b2}p=42$ and $color{#4257b2}q=2$. As a result the root could be of the form $color{#4257b2}dfrac{42}{2}$ and the factors of the form $color{#4257b2}dfrac{42}{2}$ are $color{#4257b2}pm 1, pm 2, pm 3, pm 6, pm 7, pm 14, pm 21, pm 42, pm dfrac{3}{2}, pm dfrac{7}{2}, pm dfrac{21}{2}$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
y=2x^{3}-17x^{2}+23x+42
$$

$$
y(1)=2 (1)^{3}-17 (1)^{2}+23(1)+42=50
$$

$$
y(-1)=2 (-1)^{3}-17 (-1)^{2}+23(-1)+42=0
$$

By the factor theorem, $color{#4257b2}(x+1)$ is a factor of the function $color{#4257b2}y$. Now we can divide the function $color{#4257b2}y$ by the factor term $color{#4257b2}(x+1)$ to find the remaining factors.

$$
polylongdiv{2x^3-17x^2+23x+42}{x+1}
$$

So the function $color{#4257b2}y$ can be rewrite as $color{#4257b2}y=left(x+1right)left(2x^{2}-19x+42right)$. Now the next step is to factor the quadratic function $color{#4257b2}2x^{2}-19x+42$.

$$
y=left(x+1right)left(2x^{2}-19x+42right)
$$

$$
y=left(x+1right)left(x-6right)left(2x-7right)
$$

Now to find the zeros of the function $color{#4257b2}y$ we can make each bracket equals zero to find the values of $color{#4257b2}x$ which makes the function equals zero.

$$
x+1=0, x-6=0 text{or} 2x-7=0
$$

$$
x=-1, x=6 text{or} x=dfrac{7}{2}
$$

So the zeros of the function $color{#4257b2}y$ are $color{#c34632}x=-1, x=6 text{or} x=dfrac{7}{2}$.

b) We need to write the polynomial equation whose roots are the zeros of the function in part a). First we can write the factors which makes the function $color{#4257b2}y$ equals zero

$$
because text{The zeros are}x=-1, x=6 text{and} x=dfrac{7}{2}
$$

$$
therefore text{The factors are}(x+1), (x-6) text{and} (2x-7)
$$

Now we can write an equation contains these factors in the left side and equals zero in the right side.

$$
(x+1)(x-6)(2x-7)=0
$$

But we know that if there is any number multiplied by these factor it will not change the roots of the equation, so we can write the general equation for these roots as follows:

$$
a(x+1)(x-6)(2x-7)=0
$$

Where $color{#4257b2}a$ in any real number.

So the polynomial equation is $color{#c34632}a(x+1)(x-6)(2x-7)=0$.

$$
text{color{Brown}(a) $x=-1, x=6 {color{Black}text{or}} x=dfrac{7}{2}$
\
\
\
(b) $a(x+1)(x-6)(2x-7)=0$}
$$

Since we need to solve the equation $color{#4257b2}x^{3}+12x^{2}+21x-4=x^{4}-2x^{3}-13x^{2}-4$, we need to make one side equals zero, so we can subtract $color{#4257b2}x^{3}+12x^{2}+21x-4$ from each side.

$$
x^{3}+12x^{2}+21x-4=x^{4}-2x^{3}-13x^{2}-4
$$

$$
0=x^{4}-2x^{3}-13x^{2}-4-x^{3}-12x^{2}-21x+4
$$

$$
x^{4}-3x^{3}-25x^{2}-21x=0
$$

Now we note that all terms contain $color{#4257b2}x$, so we can take it as a common factor.

$$
xleft(x^{3}-3x^{2}-25x-21right)=0 (1)
$$

Now we have a cubic equation, so we can use two different strategies to find the solutions as follows:

(a) Using the factor theorem

Since we need to solve the equation $color{#4257b2}xleft(x^{3}-3x^{2}-25x-21right)=0$, we can use the factor theorem and the related polynomial function to determine one factor of the cubic function $color{#4257b2}f(x)=x^{3}-3x^{2}-25x-21$ where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our cubic equation is $color{#4257b2}f(x)=x^{3}-3x^{2}-25x-21$, so $color{#4257b2}p=21$ and $color{#4257b2}q=1$. As a result the root could be of the form $color{#4257b2}dfrac{21}{1}$ and the factors of the form $color{#4257b2}dfrac{21}{1}$ are $color{#4257b2}pm 1, pm 3, pm 7, pm 21$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=x^{3}-3x^{2}-25x-21
$$

$$
f(1)=(1)^{3}-3 (1)^{2}-25(1)-21=-48
$$

$$
f(-1)=(-1)^{3}-3 (-1)^{2}-25(-1)-21=0
$$

By the factor theorem, $color{#4257b2}(x+1)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x+1)$ to find the remaining factors.

$$
polylongdiv{x^{3}-3x^{2}-25x-21}{x+1}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x+1right)left(x^{2}-4x-21right)$. Now the next step is to factor the quadratic function $color{#4257b2}x^{2}-4x-21$.

$$
f(x)=left(x+1right)left(x^{2}-4x-21right)
$$

$$
f(x)=left(x+1right)left(x-7right)left(x+3right)
$$

Now we found the factor of the cubic function $color{#4257b2}x^{3}-3x^{2}-25x-21$, so we can substitute in our equation (1) as follows:

$$
xleft(x^{3}-3x^{2}-25x-21right)=0
$$

$$
xleft(x+1right)left(x-7right)left(x+3right)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$

$$
x=0, x+1=0, x-7=0 text{or} x+3=0
$$

$$
x=0, x=-1, x=7 text{or} x=-3
$$

So the solutions of the equation $color{#4257b2}$ are $color{#c34632}x=0, x=-1, x=7 text{or} x=-3$.

(b) Factoring by grouping

Since we need to solve the equation $color{#4257b2}xleft(x^{3}-3x^{2}-25x-21right)=0$, we can split $color{#4257b2}-25x$ to $color{#4257b2}-4x-21x$.

$$
xleft(x^{3}-3x^{2}-25x-21right)=0
$$

$$
xleft(x^{3}-3x^{2}-4x-21x-21right)=0
$$

$$
xleft[left(x^{3}-3x^{2}-4xright)+left(-21x-21right)right]=0
$$

Now we split our cubic function to two groups, so we can factor each of them by taking $color{#4257b2}x$ as a common factor from the first group and take $color{#4257b2}-21$ as a common factor from the second group.

$$
xleft[xleft(x^{2}-3x-4right)-21left(x+1right)right]=0
$$

Now we have a quadratic function, so we can factor it.

$$
xleft[xleft(x-4right)left(x+1right)-21left(x+1right)right]=0
$$

Now we note that the two terms each of them contains the bracket $color{#4257b2}(x+1)$, so we can take it as a common factor.

$$
x(x+1)left[x(x-4)-21right]=0
$$

$$
x(x+1)left[x^{2}-4x-21right]=0
$$

Now we can factor the quadratic function $color{#4257b2}x^{2}-4x-21$.

$$
x(x+1)(x-7)(x+3)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$

$$
x=0, x+1=0, x-7=0 text{or} x+3=0
$$

$$
x=0, x=-1, x=7 text{or} x=-3
$$

So the solutions of the equation are $color{#c34632}x=0, x=-1, x=7 text{or} x=-3$.

$$
text{color{Brown}$x=0, x=-1, x=7 {color{Black}text{or}} x=-3$}
$$

We need to determine the zeros of the function
$color{#4257b2}f(x)=2x^{4}-11x^{3}-37x^{2}+156x$. First, we note that all terms of the function contain $color{#4257b2}x$, so we can take it as a common factor.

$$
f(x)=2x^{4}-11x^{3}-37x^{2}+156x
$$

$$
f(x)=xleft(2x^{3}-11x^{2}-37x+156right)
$$

Now we can split $color{#4257b2}-37x$ to $color{#4257b2}15 x-52 x$.

$$
f(x)=xleft(2x^{3}-11x^{2}-37x+156right)
$$

$$
f(x)=xleft(2x^{3}-11x^{2}+15x-52x+156right)
$$

$$
f(x)=xleft[left(2x^{3}-11x^{2}+15xright)+left(-52x+156right)right]
$$

Now we split our cubic function to two groups, so we can factor each of them by taking $color{#4257b2}x$ as a common factor from the first group and take $color{#4257b2}-52$ as a common factor from the second group.

$$
f(x)=xleft[xleft(2x^{2}-11x+15right)-52left(x-3right)right]
$$

Now we have a quadratic function, so we can factor it.

$$
f(x)=xleft[xleft(2x-5right)left(x-3right)-52left(x-3right)right]
$$

Now we note that the two terms each of them contains the bracket $color{#4257b2}(x-3)$, so we can take it as a common factor.

$$
f(x)=x(x-3)left[x(2x-5)-52right]
$$

$$
x(x-3)left[2x^{2}-5x-52right]
$$

Now we can factor the quadratic function $color{#4257b2}2x^{2}-5x-52$.

$$
x(x-3)(x+4)(2x-13)
$$

Now we found the factors of the function $color{#4257b2}f(x)$, so the next step is to make this function equals zero to find the values of $color{#4257b2}x$ which makes the function zero.

$$
x(x-3)(x+4)(2x-13)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$

$$
x=0, x-3=0, x+4=0 text{or} 2x-13=0
$$

$$
x=0, x=3, x=-4 text{or} x=dfrac{13}{2}
$$

So the zeros of the function $color{#4257b2}f(x)$ are $color{#c34632}x=0, x=3, x=-4 text{or} x=dfrac{13}{2}$.

Now we can use the graphing technology to verify our solutions. First we will graph the function $color{#4257b2}f(x)$ and then find the points where the graph will intersect the x-axis and then find the values of $color{#4257b2}x$ at these points to find the zeros of the function $color{#4257b2}f(x)$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the value of the function equals zero.

We note from the graph of the function $color{#4257b2}f(x)$ that the function intersects the x-axis at the points $color{#4257b2}A, B, C$ and $color{#4257b2}D$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}x=-4, x=0, x=3$ and $color{#4257b2}x=6.5$, so the zeros of the function $color{#4257b2}f(x)$ are $color{#c34632}x=-4, x=0, x=3$ and $color{#c34632}x=6.5$ and this verifies our solutions algebraically.

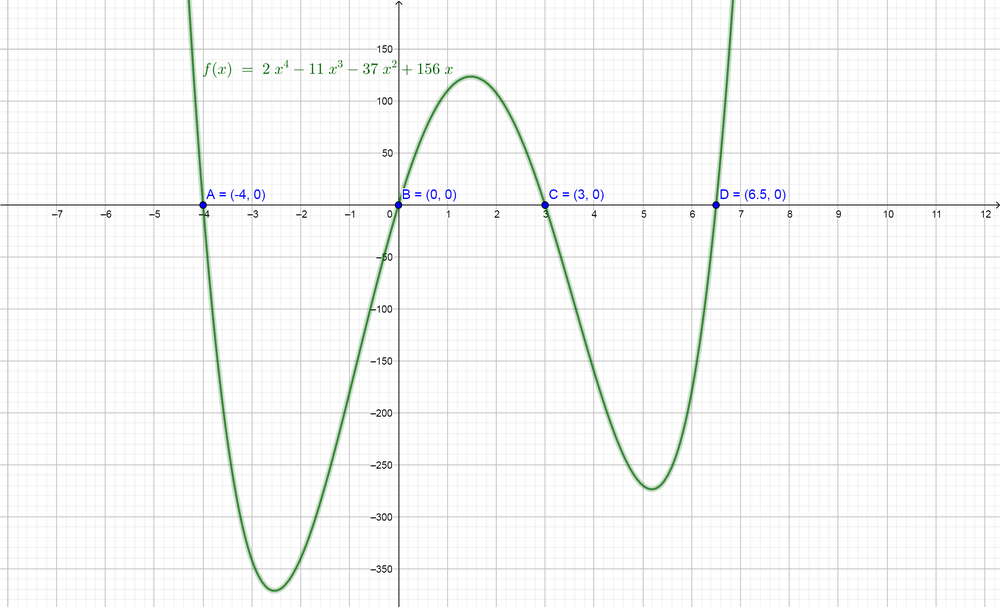
$$
text{color{Brown}$x=-4, x=0, x=3$ {color{Black}text{or}} $x=6.5$}
$$

(a) We would like to state the zeros of the functions $color{#4257b2}f(x)=xleft(x-2right)^{2}left(x+5right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
f(x)=xleft(x-2right)^{2}left(x+5right)
$$

$$
f(x)=xleft(x-2right)^{2}left(x+5right)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}f(x)$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
xleft(x-2right)^{2}left(x+5right)=0
$$

$$
x=0, (x-2)^{2}=0 text{or} x+5=0
$$

$$
x=0, x=2 text{or} x=-5
$$

Note that the bracket $color{#4257b2}left(x-2right)^{2}$ has two zeros but the two zeros are equal $color{#4257b2}2$, so we write it just once.

So the zeros of the function $color{#4257b2}f(x)$ are $color{#c34632}x=0, x=2 {color{Black}text{or}} x=-5$

(b) We would like to state the zeros of the functions $color{#4257b2}f(x)=left(x^{3}+1right)left(x-17right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
f(x)=left(x^{3}+1right)left(x-17right)
$$

$$
f(x)=left(x^{3}+1right)left(x-17right)=0
$$

$$
left(x^{3}+1right)left(x-17right)=0
$$

Now we have a cubic function on the form $color{#4257b2}x^{3}+a^{3}$, so we can factor it where $color{#4257b2}x^{3}+a^{3}=(x+a)(x^{2}-ax+a^{2})$.

$$
left(x^{3}+1right)left(x-17right)=0
$$

$$
left(x+1right)left(x^{2}-x+1right)left(x-17right)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}f(x)$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
x+1=0, x^{2}-x+1=0 text{or} x-17=0
$$

But we note that the quadratic equation $color{#4257b2}x^{2}-x+1=0$ has no real solutions, so there is no zeros for this equation.

$$
x+1=0 text{or} x-17=0
$$

$$
x=-1 text{or} x=17
$$

So the zeros of the function $color{#4257b2}f(x)$ are $color{#c34632}x=-1 {color{Black}text{or}} x=17$

(c) We would like to state the zeros of the functions $color{#4257b2}f(x)=left(x^{2}+36right)left(8x-16right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
f(x)=left(x^{2}+36right)left(8x-16right)
$$

$$
f(x)=left(x^{2}+36right)left(8x-16right)=0
$$

$$
left(x^{2}+36right)left(8x-16right)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}f(x)$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
x^{2}+36=0 text{or} 8x-16=0
$$

But we note that the quadratic equation $color{#4257b2}x^{2}+36=0$ has the imaginary solutions $color{#4257b2}x=pm 6i$, so there is no zeros for this equation.

$$
8x-16=0
$$

$$
8x=16
$$

$$
x=2
$$

So the zero of the function $color{#4257b2}f(x)$ is $color{#c34632}x=2$

(d) We would like to state the zeros of the functions $color{#4257b2}f(x)=-3x^{3}left(2x+4right)left(x^{2}-25right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
f(x)=-3x^{3}left(2x+4right)left(x^{2}-25right)
$$

$$
f(x)=-3x^{3}left(2x+4right)left(x^{2}-25right)=0
$$

$$
-3x^{3}left(2x+4right)left(x^{2}-25right)=0
$$

Now we have a quadratic function on the form $color{#4257b2}x^{2}-a^{2}$, so we can factor it where $color{#4257b2}x^{2}-a^{2}=(x+a)(x-a)$.

$$
-3x^{3}left(2x+4right)left(x^{2}-25right)=0
$$

$$
-3x^{3}left(2x+4right)left(x+5right)left(x-5right)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}f(x)$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
-3x^{3}=0, 2x+4=0, x+5=0 text{or} x-5=0
$$

$$
x=0, x=-2, x=-5 text{or} x=5
$$

Note that the equation $color{#4257b2}-3x^{3}$ has three zeros but each of them equals zero, so we write it just once.

So the zeros of the function $color{#4257b2}f(x)$ are $color{#c34632}x=0, x=-2, x=-5 {color{Black}text{or}} x=5$

(e) We would like to state the zeros of the functions $color{#4257b2}f(x)=left(x^{2}-x-12right)left(3xright)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
f(x)=left(x^{2}-x-12right)left(3xright)
$$

$$
f(x)=left(x^{2}-x-12right)left(3xright)=0
$$

$$
left(x^{2}-x-12right)left(3xright)=0
$$

Now we have a quadratic function, so we can factor it.

$$
left(x^{2}-x-12right)left(3xright)=0
$$

$$
left(x-4right)left(x+3right)left(3xright)=0
$$

Now we can use the zero-factor property to find the zeros of the functions $color{#4257b2}f(x)$. Note that the meaning of the zeros of the function is to find the values of $color{#4257b2}x$ which makes the function equal zero.

$$
x-4=0, x+3=0 text{or} 3x=0
$$

$$
x=4, x=-3 text{or} x=0
$$

So the zeros of the function $color{#4257b2}f(x)$ are $color{#c34632}x=-3, x=0 {color{Black}text{or}} x=4$

(f) We would like to state the zeros of the functions $color{#4257b2}f(x)=left(x+1right)left(x^{2}+2x+1right)$. First, to find the zeros of the function we need to make the function to be equal zero.

$$
f(x)=left(x+1right)left(x^{2}+2x+1right)
$$

$$
f(x)=left(x+1right)left(x^{2}+2x+1right)=0
$$

$$
left(x+1right)left(x^{2}+2x+1right)=0
$$

Now we have a quadratic function, so we can factor it.

$$
left(x+1right)left(x^{2}+2x+1right)=0
$$

$$
left(x+1right)left(x+1right)left(x+1right)=0
$$

$$
left(x+1right)^{3}=0
$$

$$
x+1=0
$$

$$
x=-1
$$

Note that this function is simplified to $color{#4257b2}left(x+1right)^{3}$, so the zeros of this function all of them equal $color{#4257b2}-1$ and this is the reason we write it just once.

So the zero of the function $color{#4257b2}f(x)$ are $color{#c34632}x=-1$

$$
text{color{Brown}(a) $x=0, x=2 {color{Black}text{or}} x=-5$
\
\
Large{color{Brown}(b) $x=-1 {color{Black}text{or}} x=17$}
\
\
Large{color{Brown}(c) $x=2$}
\
\
Large{color{Brown}(d) $x=0, x=-2, x=-5 {color{Black}text{or}} x=5$}
\
\
Large{color{Brown}(e) $x=-3, x=0 {color{Black}text{or}} x=4$}
\
\
Large{color{Brown}(f) $x=-1$}}
$$

(a) Since we need to determine the roots of the equation
$color{#4257b2}x^{3}-8x^{2}-3x+90=0$, we can let $color{#4257b2}f(x)=x^{3}-8x^{2}-3x+90$ and then use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=x^{3}-8x^{2}-3x+90$, so $color{#4257b2}p=90$ and $color{#4257b2}q=1$. As a result the root could be of the form $color{#4257b2}dfrac{90}{1}=90$ and the factors of it are $color{#4257b2}pm 1, pm 2, pm 3, pm 5, pm 6, pm 9, pm 10, pm 15, pm 18, pm 30, pm 60, pm 90$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=x^{3}-8x^{2}-3x+90
$$

$$
f(1)=(1)^{3}-8 (1)^{2}-3(1)+90=80
$$

$$
f(-1)=(-1)^{3}-8 (-1)^{2}-3(-1)+90=84
$$

$$
f(2)=(2)^{3}-8 (2)^{2}-3(2)+90=60
$$

$$
f(-2)=(-2)^{3}-8 (-2)^{2}-3(-2)+90=56
$$

$$
f(3)=(3)^{3}-8 (3)^{2}-3(3)+90=36
$$

$$
f(-3)=(-3)^{3}-8 (-3)^{2}-3(-3)+90=0
$$

By the factor theorem, $color{#4257b2}(x+3)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x+3)$ to find the remaining factors.

$$
polylongdiv{x^3-8x^2-3x+90}{x+3}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x+3right)left(x^{2}-11x+30right)$. Now the next step is to factor the quadratic function $color{#4257b2}x^{2}-11x+30$.

$$
f(x)=left(x+3right)left(x^{2}-11x+30right)
$$

$$
f(x)=left(x+3right)left(x-5right)left(x-6right)
$$

Now we found the factors of the function $color{#4257b2}f(x)=x^3-8x^2-3x+90$, so we can substitute in our equation to find the solutions of it.

$$
x^3-8x^2-3x+90=0
$$

$$
left(x+3right)left(x-5right)left(x-6right)=0
$$

Now we can use the zero-factor property.

$$
x+3=0, x-5=0 text{or} x-6=0
$$

$$
x=-3, x=5 text{or} x=6
$$

So the solutions of the equation are $color{#c34632}x=-3, x=5 {color{Black}text{or}} x=6$.

(b) Since we need to determine the roots of the equation
$color{#4257b2}x^{4}+9x^{3}+21x^{2}-x-30=0$, we can let $color{#4257b2}f(x)=x^{4}+9x^{3}+21x^{2}-x-30$ and then use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=x^{4}+9x^{3}+21x^{2}-x-30$, so $color{#4257b2}p=30$ and $color{#4257b2}q=1$. As a result the root could be of the form $color{#4257b2}dfrac{30}{1}=30$ and the factors of it are $color{#4257b2}pm 1, pm 2, pm 3, pm 5, pm 6, pm 10, pm 15, pm 30$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=x^{4}+9x^{3}+21x^{2}-x-30
$$

$$
f(1)=(1)^{4}+9(1)^{3}+21(1)^{2}-(1)-30=0
$$

By the factor theorem, $color{#4257b2}(x-1)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x-1)$ to find the remaining factors.

$$
polylongdiv{x^{4}+9x^{3}+21x^{2}-x-30}{x-1}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x-1right)left(x^{3}+10x^{2}+31x+30right) (1)$. Now we note that we have a cubic function, so we can use the factor theorem one more time to find another factor but this once for the cubic function $color{#4257b2}y=x^{3}+10x^{2}+31x+30$. Note that we let $color{#4257b2}f(x)=(x-1) [y(x)]$

$$
y=x^{3}+10x^{2}+31x+30
$$

$$
y(1)=(1)^{3}+10(1)^{2}+31(1)+30=72
$$

$$
y(-1)=(-1)^{3}+10(-1)^{2}+31(-1)+30=8
$$

$$
y(2)=(2)^{3}+10(2)^{2}+31(2)+30=140
$$

$$
y(-2)=(-2)^{3}+10(-2)^{2}+31(-2)+30=0
$$

By the factor theorem, $color{#4257b2}(x+2)$ is a factor of the function $color{#4257b2}y$. Now we can divide the function $color{#4257b2}y$ by the factor term $color{#4257b2}(x+2)$ to find the remaining factors.

$$
polylongdiv{x^{3}+10x^{2}+31x+30}{x+2}
$$

So the function $color{#4257b2}y$ can be rewrite as $color{#4257b2}y=left(x+2right)left(x^{2}+8x+15right)$. Now the next step is to factor the quadratic function $color{#4257b2}x^{2}+8x+15$.

$$
y=left(x+2right)left(x^{2}+8x+15right)
$$

$$
y=left(x+2right)left(x+5right)left(x+3right)
$$

Now we can substitute the function $color{#4257b2}y$ in the function (1) for $color{#4257b2}f(x)$ to find the factors of the function $color{#4257b2}$.

$$
f(x)=(x-1)(x^{3}+10x^{2}+31x+30)
$$

$$
f(x)=(x-1)(x+2)(x+5)(x+3)
$$

Now we found the factors of the function $color{#4257b2}f(x)=x^{4}+9x^{3}+21x^{2}-x-30$, so we can substitute in our equation to find the solutions of it.

$$
x^{4}+9x^{3}+21x^{2}-x-30=0
$$

$$
(x-1)(x+2)(x+5)(x+3)=0
$$

Now we can use the zero-factor property.

$$
x-1=0, x+2=0, x+5=0 text{or} x+3=0
$$

$$
x=1, x=-2, x=-5 text{or} x=-3
$$

So the solutions of the equation are $color{#c34632}x=-5, x=-3, x=-2 {color{Black}text{or}} x=1$.

(c) Since we need to determine the roots of the equation
$color{#4257b2}2x^{3}-5x^{2}-4x+3=0$, we can let $color{#4257b2}f(x)=2x^{3}-5x^{2}-4x+3$ and then use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=2x^{3}-5x^{2}-4x+3$, so $color{#4257b2}p=3$ and $color{#4257b2}q=2$. As a result the root could be of the form $color{#4257b2}dfrac{3}{2}$ and the factors of it are $color{#4257b2}pm 1, pm 3, pm dfrac{1}{2}, pm dfrac{3}{2}$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=2x^{3}-5x^{2}-4x+3
$$

$$
f(1)=2(1)^{3}-5(1)^{2}-4(1)+3=-4
$$

$$
f(-1)=2(-1)^{3}-5(-1)^{2}-4(-1)+3=0
$$

By the factor theorem, $color{#4257b2}(x+1)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x+1)$ to find the remaining factors.

$$
polylongdiv{2x^{3}-5x^{2}-4x+3}{x+1}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x+1right)left(2x^{2}-7x+3right)$. Now the next step is to factor the quadratic function $color{#4257b2}2x^{2}-7x+3$.

$$
f(x)=left(x+1right)left(2x^{2}-7x+3right)
$$

$$
f(x)=left(x+1right)left(x-3right)left(2x-1right)
$$

Now we found the factors of the function $color{#4257b2}f(x)=2x^3-5x^2-4x+3$, so we can substitute in our equation to find the solutions of it.

$$
2x^3-5x^2-4x+3=0
$$

$$
left(x+1right)left(x-3right)left(2x-1right)=0
$$

Now we can use the zero-factor property.

$$
x+1=0, x-3=0 text{or} 2x-1=0
$$

$$
x=-1, x=3 text{or} x=dfrac{1}{2}
$$

So the solutions of the equation are $color{#c34632}x=-1, x=dfrac{1}{2} {color{Black}text{or}} x=3$.

(d) We need to determine the roots of the equation
$color{#4257b2}2x^{3}+3x^{2}=5x+6$. First, we can subtract $color{#4257b2}5x+6$ from each side to make the right side equals zero.

$$
2x^{3}+3x^{2}=5x+6
$$

$$
2x^{3}+3x^{2}-5x-6=0
$$

Now we can let $color{#4257b2}f(x)=2x^{3}+3x^{2}-5x-6$ and then use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=2x^{3}+3x^{2}-5x-6$, so $color{#4257b2}p=6$ and $color{#4257b2}q=2$. As a result the root could be of the form $color{#4257b2}dfrac{6}{2}$ and the factors of it are $color{#4257b2}pm 1, pm 2, pm 3pm, pm 6, dfrac{1}{2}, pm dfrac{3}{2}$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=2x^{3}+3x^{2}-5x-6
$$

$$
f(1)=2(1)^{3}+3(1)^{2}-5(1)-6=-6
$$

$$
f(-1)=2(-1)^{3}+3(-1)^{2}-5(-1)-6=0
$$

By the factor theorem, $color{#4257b2}(x+1)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x+1)$ to find the remaining factors.

$$
polylongdiv{2x^{3}+3x^{2}-5x-6}{x+1}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x+1right)left(2x^{2}+x-6right)$. Now the next step is to factor the quadratic function $color{#4257b2}2x^{2}+x-6$.

$$
f(x)=left(x+1right)left(2x^{2}+x-6right)
$$

$$
f(x)=left(x+1right)left(x+2right)left(2x-3right)
$$

Now we found the factors of the function $color{#4257b2}f(x)=2x^{3}+3x^{2}-5x-6$, so we can substitute in our equation to find the solutions of it.

$$
2x^{3}+3x^{2}-5x-6=0
$$

$$
left(x+1right)left(x+2right)left(2x-3right)=0
$$

Now we can use the zero-factor property.

$$
x+1=0, x+2=0 text{or} 2x-3=0
$$

$$
x=-1, x=-2 text{or} x=dfrac{3}{2}
$$

So the solutions of the equation are $color{#c34632}x=-2, x=-1 {color{Black}text{or}} x=dfrac{3}{2}$.

(e) We need to determine the roots of the equation
$color{#4257b2}4x^{4}-4x^{3}-51x^{2}+106x=40$. First, we can subtract $color{#4257b2}40$ from each side to make the right side equals zero.

$$
4x^{4}-4x^{3}-51x^{2}+106x=40
$$

$$
4x^{4}-4x^{3}-51x^{2}+106x-40=0
$$

Now we can let $color{#4257b2}f(x)=4x^{4}-4x^{3}-51x^{2}+106x-40$ and then use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=4x^{4}-4x^{3}-51x^{2}+106x-40$, so $color{#4257b2}p=40$ and $color{#4257b2}q=4$. As a result the root could be of the form $color{#4257b2}dfrac{40}{4}$ and the factors of it are $color{#4257b2}pm 1, pm 2, pm 4, pm 5, pm 8, pm 10, pm 20, pm 40, pm dfrac{1}{2}, pm dfrac{5}{2}, pm dfrac{1}{4}, pm dfrac{5}{4}$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=4x^{4}-4x^{3}-51x^{2}+106x-40
$$

$$
f(1)=4(1)^{4}-4(1)^{3}-51(1)^{2}+106(1)-40=15
$$

$$
f(-1)=4(-1)^{4}-4(-1)^{3}-51(-1)^{2}+106(-1)-40=-189
$$

$$
f(2)=4(2)^{4}-4(2)^{3}-51(2)^{2}+106(2)-40=0
$$

By the factor theorem, $color{#4257b2}(x-2)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x-2)$ to find the remaining factors.

$$
polylongdiv{4x^{4}-4x^{3}-51x^{2}+106x-40}{x-2}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x-2right)left(4x^{3}+4x^{2}-43x+20right) (1)$. Now we note that we have a cubic function, so we can use the factor theorem one more time to find another factor but this once for the cubic function $color{#4257b2}y=4x^{3}+4x^{2}-43x+20$. Note that we let $color{#4257b2}f(x)=(x-2) [y(x)]$

$$
y=4x^{3}+4x^{2}-43x+20
$$

$$
y(4)=4(4)^{3}+4(4)^{2}-43(4)+20=168
$$

$$
y(-4)=4(-4)^{3}+4(-4)^{2}-43(-4)+20=0
$$

By the factor theorem, $color{#4257b2}(x+4)$ is a factor of the function $color{#4257b2}y$. Now we can divide the function $color{#4257b2}y$ by the factor term $color{#4257b2}(x+4)$ to find the remaining factors.

$$
polylongdiv{4x^{3}+4x^{2}-43x+20}{x+4}
$$

So the function $color{#4257b2}y$ can be rewrite as $color{#4257b2}y=left(x+4right)left(4x^{2}-12x+5right)$. Now the next step is to factor the quadratic function $color{#4257b2}4x^{2}-12x+5$.

$$
y=left(x+4right)left(4x^{2}-12x+5right)
$$

$$
y=left(x+4right)left(2x-1right)left(2x-5right)
$$

Now we can substitute the function $color{#4257b2}y$ in the function (1) for $color{#4257b2}f(x)$ to find the factors of the function $color{#4257b2}$.

$$
f(x)=(x-2)(4x^{3}+4x^{2}-43x+20)
$$

$$
f(x)=left(x-2right)left(x+4right)left(2x-1right)left(2x-5right)
$$

Now we found the factors of the function $color{#4257b2}f(x)=4x^{4}-4x^{3}-51x^{2}+106x-40=0$, so we can substitute in our equation to find the solutions of it.

$$
4x^{4}-4x^{3}-51x^{2}+106x-40=0
$$

$$
(x-2)(x+4)(2x-1)(2x-5)=0
$$

Now we can use the zero-factor property.

$$
x-2=0, x+4=0, 2x-1=0 text{or} 2x-5=0
$$

$$
x=2, x=-4, x=dfrac{1}{2} text{or} x=dfrac{5}{2}
$$

So the solutions of the equation are $color{#c34632}x=-4, x=dfrac{1}{2}, x=2 {color{Black}text{or}} x=dfrac{5}{2}$.

(f) We need to determine the roots of the equation
$color{#4257b2}12x^{3}-44x^{2}=-49x+15$. First, we can add $color{#4257b2}49x-15$ to each side to make the right side equals zero.

$$
12x^{3}-44x^{2}=-49x+15
$$

$$
12x^{3}-44x^{2}+49x-15=0
$$

Now we can let $color{#4257b2}f(x)=12x^{3}-44x^{2}+49x-15$ and then use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=12x^{3}-44x^{2}+49x-15$, so $color{#4257b2}p=15$ and $color{#4257b2}q=12$. As a result the root could be of the form $color{#4257b2}dfrac{15}{12}$ and the factors of it are $color{#4257b2}pm 1, pm 3, pm 5pm, pm 15, dfrac{1}{2}, pm dfrac{3}{2}, pm dfrac{5}{2}, pm dfrac{15}{2}, pm dfrac{1}{3}, pm dfrac{5}{3}, pm dfrac{1}{4}, pm dfrac{3}{4}, pm dfrac{5}{4}, pm dfrac{15}{4}, pm dfrac{1}{6}, pm dfrac{5}{6}, pm dfrac{1}{12}, pm dfrac{5}{12}$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=12x^{3}-44x^{2}+49x-15
$$

$$
fleft(dfrac{1}{2}right)=12left(dfrac{1}{2}right)^{3}-44left(dfrac{1}{2}right)^{2}+49left(dfrac{1}{2}right)-15=0
$$

By the factor theorem, $color{#4257b2}left(2x-1right)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}left(2x-1right)$ to find the remaining factors.

$$
polylongdiv{12x^{3}-44x^{2}+49x-15}{2x-1}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(2x-1right)left(6x^{2}-19x+15right)$. Now the next step is to factor the quadratic function $color{#4257b2}12x^{2}-38x+30$.

$$
f(x)=left(2x-1right)left(6x^{2}-19x+15right)
$$

$$
f(x)=left(2x-1right)left(3x-5right)left(2x-3right)
$$

Now we found the factors of the function $color{#4257b2}f(x)=12x^{3}-44x^{2}+49x-15$, so we can substitute in our equation to find the solutions of it.

$$
12x^{3}-44x^{2}+49x-15=0
$$

$$
left(2x-1right)left(3x-5right)left(2x-3right)=0
$$

Now we can use the zero-factor property.

$$
2x-1=0, 3x-5=0 text{or} 2x-3=0
$$

$$
x=dfrac{1}{2}, x=dfrac{5}{3} text{or} x=dfrac{3}{2}
$$

So the solutions of the equation are $color{#c34632}x=dfrac{1}{2}, x=dfrac{3}{2} {color{Black}text{or}} x=dfrac{5}{3}$.

Large{$text{color{Brown}(a) $x=-3, x=5 {color{Black}text{or}} x=6$
\
\
(b) $x=-5, x=-3, x=-2 {color{Black}text{or}} x=1$
\
\
(c) $x=-1, x=dfrac{1}{2} {color{Black}text{or}} x=3$
\
\
(d) $x=-2, x=-1 {color{Black}text{or}} x=dfrac{3}{2}$
\
\
(e) $x=-4, x=dfrac{1}{2}, x=2 {color{Black}text{or}} x=dfrac{5}{2}$
\
\
(f) $x=dfrac{1}{2}, x=dfrac{3}{2} {color{Black}text{or}} x=dfrac{5}{3}$}$

(a) We would like to use the graph technology to find the real roots for the equation $color{#4257b2}x^{3}-7x+6=0$. First, we note that the left side is a cubic function and the right side equals zero, so we can graph the cubic function on the plane and then find the points which the graph intersects the x-axis and then find the value of $color{#4257b2}x$ at these points which will be the roots of the equation. Note that we will find the points where the graph will intersect the x-axis because the right side equals zero.

We note from the graph that the graph of the function $color{#4257b2}f(x)=x^{3}-7x+6$ intersects the x-axis at the points $color{#4257b2}A, B$ and $color{#4257b2}C$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}x=-3, x=1$ and $color{#4257b2}x=2$, so the roots of the equation
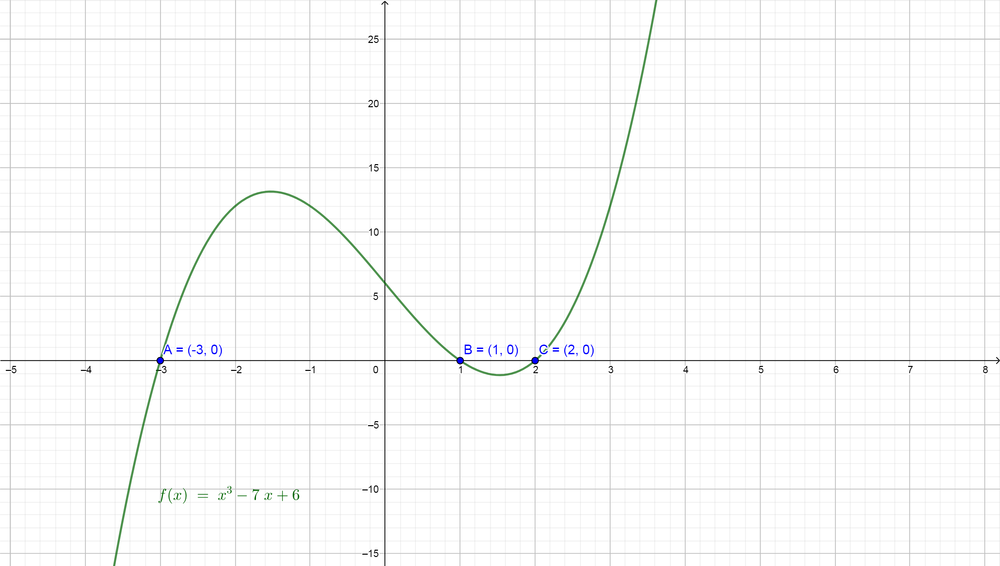
$color{#4257b2}x^{3}-7x+6=0$ are $color{#c34632}x=-3, x=1$ and $color{#c34632}x=2$.

(b) We would like to use the graph technology to find the real roots for the equation $color{#4257b2}x^{4}-5x^{3}-17x^{2}+3x+18=0$. First, we note that the left side is a function from the fourth degree and the right side equals zero, so we can graph the function on the plane and then find the points which the graph intersects the x-axis and then find the value of $color{#4257b2}x$ at these points which will be the roots of the equation. Note that we will find the points where the graph will intersect the x-axis because the right side equals zero.

We note from the graph that the graph of the function
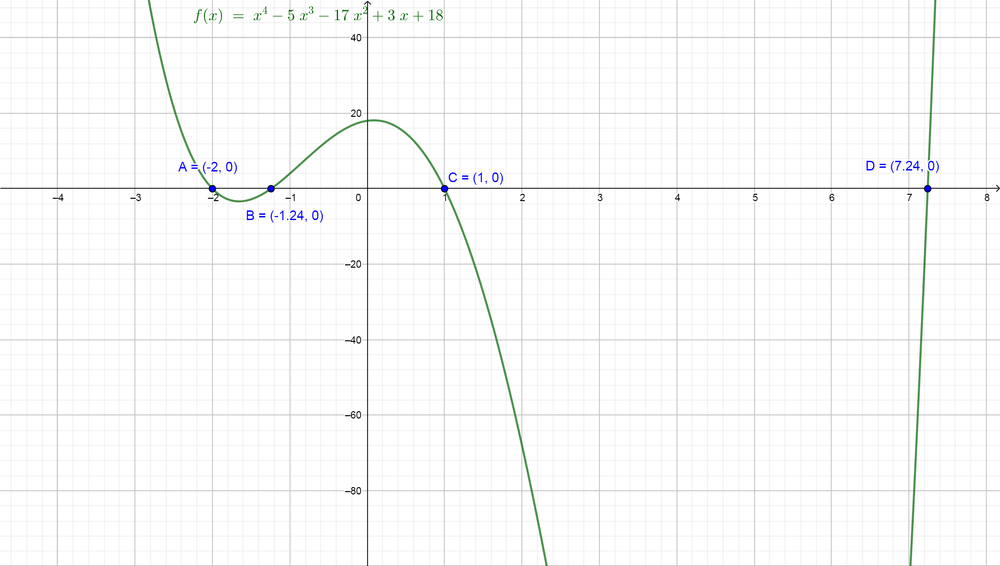
$color{#4257b2}f(x)=x^{4}-5x^{3}-17x^{2}+3x+18$ intersects the x-axis at the points $color{#4257b2}A, B, C$ and $color{#4257b2}D$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}x=-2, x=-1.24, x=1$ and $color{#4257b2}x=7.24$, so the roots of the equation
$color{#4257b2}x^{4}-5x^{3}-17x^{2}+3x+18=0$ are $color{#c34632}x=-2, x=-1.24, x=1$ and $color{#c34632}x=7.24$.

(c) We would like to use the graph technology to find the real roots for the equation $color{#4257b2}3x^{3}-2x^{2}+16=x^{4}+16x$. First, we note that the left side is a cubic function and the right side is a function from the fourth degree, so we can graph the two functions on the same plane and then find the points which the two graph intersect each others and then find the value of $color{#4257b2}x$ at these points which will be the roots of the equation.

We note from the graph that the graph of the function $color{#4257b2}f(x)=3x^{3}-2x^{2}+16$ intersects the graph $color{#4257b2}g(x)=x^{4}+16x$ at the points $color{#4257b2}A$ and $color{#4257b2}B$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}x=-2$ and $color{#4257b2}x=1$, so the roots of the equation
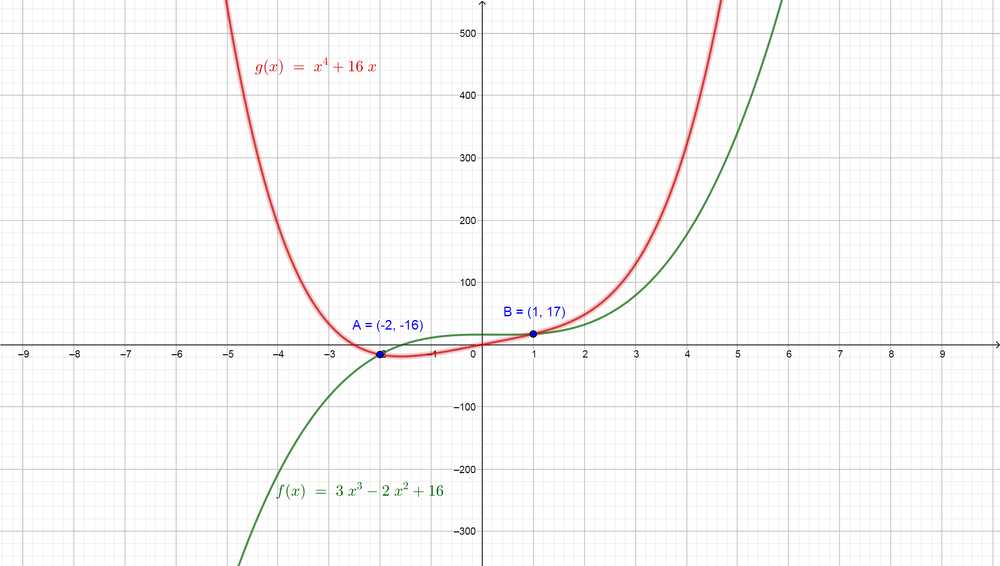
$color{#4257b2}3x^{3}-2x^{2}+16=x^{4}+16x$ are $color{#c34632}x=-2$ and $color{#c34632}x=1$.

Note that our equation is of the fourth degree but we have only two solutions and this because the two other solutions are imaginary solutions and the plane shows the real solutions only, so there are two real solutions only.

(d) We would like to use the graph technology to find the real roots for the equation $color{#4257b2}x^{5}+x^{4}=5x^{3}-x^{2}+6x$. First, we note that the left side is a function from the fifth degree and the right side is a cubic function, so we can graph the two functions on the same plane and then find the points which the two graph intersect each others and then find the value of $color{#4257b2}x$ at these points which will be the roots of the equation.

We note from the graph that the graph of the function $color{#4257b2}f(x)=x^{5}+x^{4}$ intersects the graph $color{#4257b2}g(x)=5x^{3}-x^{2}+6x$ at the points $color{#4257b2}A, B$ and $color{#4257b2}C$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}x=-3, x=0$ and $color{#4257b2}x=2$, so the roots of the equation
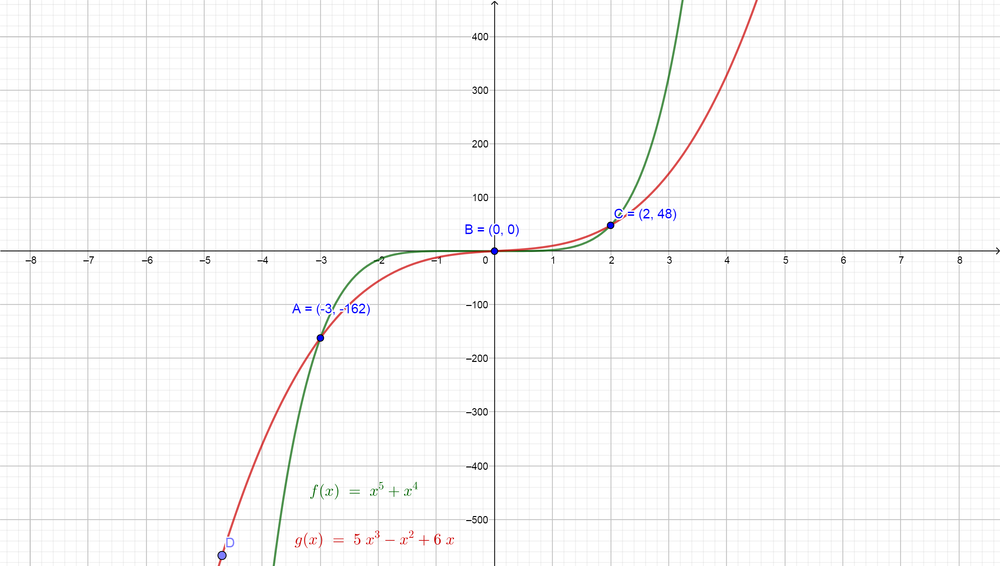
$color{#4257b2}x^{5}+x^{4}=5x^{3}-x^{2}+6x$ are $color{#c34632}x=-3, x=0$ and $color{#c34632}x=2$.

Note that our equation is of the fifth degree but we have only three solutions and this because the two other solutions are imaginary solutions and the plane shows the real solutions only, so there are two real solutions only.

(e) We would like to use the graph technology to find the real roots for the equation $color{#4257b2}105x^{3}=344x^{2}-69x-378$. First, we note that the left side is a cubic function and the right side is a quadratic function, so we can graph the two functions on the same plane and then find the points which the two graph intersect each others and then find the value of $color{#4257b2}x$ at these points which will be the roots of the equation.

We note from the graph that the graph of the function $color{#4257b2}f(x)=105x^{3}$ intersects the graph $color{#4257b2}g(x)=344x^{2}-69x-378$ at the points $color{#4257b2}A, B$ and $color{#4257b2}C$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}x=-0.86, x=1.8$ and $color{#4257b2}x=2.33$, so the roots of the equation
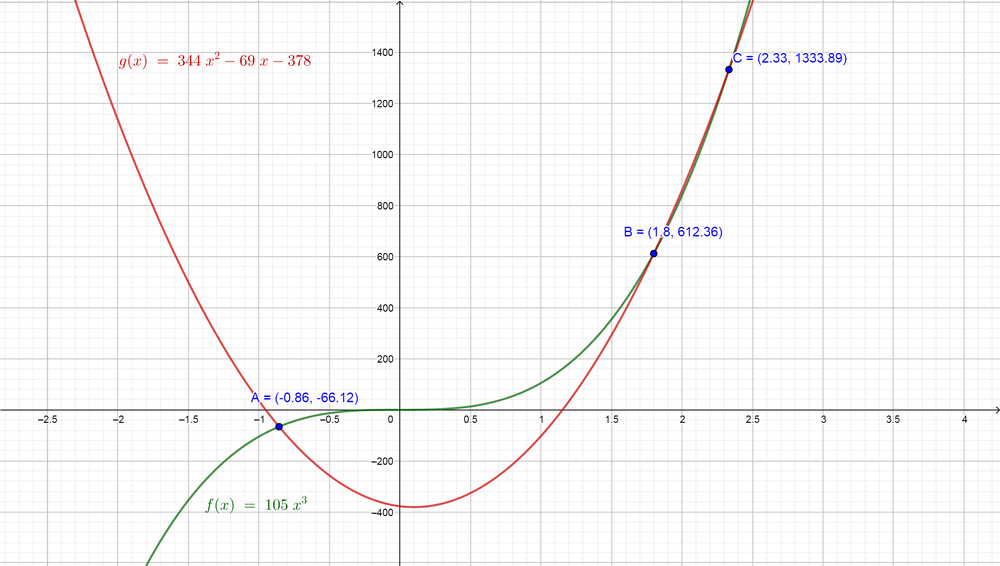
$color{#4257b2}105x^{3}=344x^{2}-69x-378$ are $color{#c34632}x=-0.86, x=1.8$ and $color{#c34632}x=2.33$.

(f) We would like to use the graph technology to find the real roots for the equation $color{#4257b2}21x^{3}-58x^{2}+10=-18 x^{4}-51 x$. First, we note that the left side is a cubic function and the right side is a function of the fourth degree, so we can graph the two functions on the same plane and then find the points which the two graph intersect each others and then find the value of $color{#4257b2}x$ at these points which will be the roots of the equation.

We note from the graph that the graph of the function
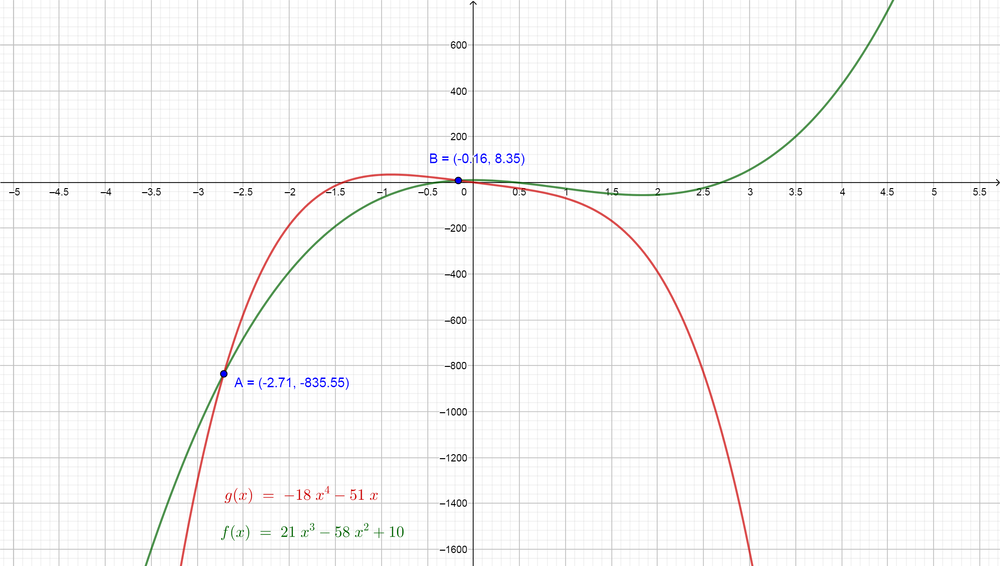
$color{#4257b2}f(x)=21x^{3}-58x^{2}+10$ intersects the graph $color{#4257b2}g(x)=-18x^{4}-51x$ at the points $color{#4257b2}A$ and $color{#4257b2}B$ and the values of $color{#4257b2}x$ at these points are $color{#4257b2}x=-2.71$ and $color{#4257b2}x=-0.16$, so the roots of the equation
$color{#4257b2}105x^{3}=344x^{2}-69x-378$ are $color{#c34632}x=-2.71$ and $color{#c34632}x=0.16$.

Note that our equation is of the fourth degree but we have only two solutions and this because the two other solutions are imaginary solutions and the plane shows the real solutions only, so there are two real solutions only.

Large{$text{color{Brown}(a) $x=-3, x=1 {color{Black}text{or}} x=2$
\
\
(b) $x=-2, x=-1.24, x=1 {color{Black}text{or}} x=7.24$
\
\
(c) $x=-2 {color{Black}text{or}} x=1$
\
\
(d) $x=-3, x=0 {color{Black}text{or}} x=2$
\
\
(e) $x=-0.86, x=1.8 {color{Black}text{or}} x=2.33$
\
\
(f) $x=-2.71 {color{Black}text{or}} x=-0.16$}$

(a) Since we need to solve the equation $color{#4257b2}x^{3}-6x^{2}-x+30=0$, we can let $color{#4257b2}f(x)=x^{3}-6x^{2}-x+30$ and then use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=x^{3}-6x^{2}-x+30$, so $color{#4257b2}p=30$ and $color{#4257b2}q=1$. As a result the root could be of the form $color{#4257b2}dfrac{30}{1}=30$ and the factors of it are $color{#4257b2}pm 1, pm 2, pm 3, pm 5, pm 6, pm 10, pm 15, pm 30$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=x^{3}-6x^{2}-x+30
$$

$$
f(1)=(1)^{3}-6(1)^{2}-(1)+30=24
$$

$$
f(-1)=(-1)^{3}-6(-1)^{2}-(-1)+30=36
$$

$$
f(2)=(2)^{3}-6(2)^{2}-(2)+30=12
$$

$$
f(-2)=(-2)^{3}-6(-2)^{2}-(-2)+30=0
$$

By the factor theorem, $color{#4257b2}(x+2)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x+2)$ to find the remaining factors.

$$
polylongdiv{x^{3}-6x^{2}-x+30}{x+2}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x+2right)left(x^{2}-8x+15right)$. Now the next step is to factor the quadratic function $color{#4257b2}x^{2}-8x+15$.

$$
f(x)=left(x+2right)left(x^{2}-8x+15right)
$$

$$
f(x)=left(x+2right)left(x-3right)left(x-5right)
$$

Now we found the factors of the function $color{#4257b2}f(x)=x^{3}-6x^{2}-x+30$, so we can substitute in our equation to find the solutions of it.

$$
x^{3}-6x^{2}-x+30=0
$$

$$
left(x+2right)left(x-3right)left(x-5right)=0
$$

Now we can use the zero-factor property.

$$
x+2=0, x-3=0 text{or} x-5=0
$$

$$
x=-2, x=3 text{or} x=5
$$

So the solutions of the equation are $color{#c34632}x=-2, x=3 {color{Black}text{or}} x=5$.

(b) We need to solve the equation $color{#4257b2}9x^{4}-42x^{3}+64x^{2}-32x=0$. First, we note that all terms of the function contain $color{#4257b2}x$, so we can take it as a common factor.

$$
9x^{4}-42x^{3}+64x^{2}-32x=0
$$

$$
xleft(9x^{3}-42x^{2}+64x-32right)=0 (1)
$$

we can let $color{#4257b2}f(x)=9x^{3}-42x^{2}+64x-32$ and then use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=9x^{3}-42x^{2}+64x-32$, so $color{#4257b2}p=32$ and $color{#4257b2}q=9$. As a result the root could be of the form $color{#4257b2}dfrac{32}{9}$ and the factors of it are $color{#4257b2}pm 1, pm 2, pm 4, pm 8, pm 16, pm 32, pm dfrac{1}{3}, pm dfrac{2}{3}, pm dfrac{4}{3}, pm dfrac{8}{3}, pm dfrac{16}{3}, pm dfrac{32}{3}, pm dfrac{1}{9}, pm dfrac{2}{9}, pm dfrac{4}{9}, pm dfrac{8}{9}, pm dfrac{16}{9}, pm dfrac{32}{9}$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=9x^{3}-42x^{2}+64x-32
$$

$$
f(1)=9(1)^{3}-42(1)^{2}+64(1)-32=-1
$$

$$
f(-1)=9(-1)^{3}-42(-1)^{2}+64(-1)-32=-147
$$

$$
f(2)=9(2)^{3}-42(2)^{2}+64(2)-32=0
$$

By the factor theorem, $color{#4257b2}(x-2)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x-2)$ to find the remaining factors.

$$
polylongdiv{9x^{3}-42x^{2}+64x-32}{x-2}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x-2right)left(9x^{2}-24x+16right)$. Now the next step is to factor the quadratic function $color{#4257b2}9x^{2}-24x+16$.

$$
f(x)=left(x-2right)left(9x^{2}-24x+16right)
$$

$$
f(x)=left(x-2right)left(3x-4right)left(3x-4right)
$$

Now we found the factors of the function $color{#4257b2}f(x)=9x^{3}-42x^{2}+64x-32$, so we can substitute in our equation (1) to find the solutions of it.

$$
xleft(9x^{3}-42x^{2}+64x-32right)=0
$$

$$
xleft(x-2right)left(3x-4right)left(3x-4right)=0
$$

Now we can use the zero-factor property.

$$
x=0, x-2=0, 3x-4=0 text{or} 3x-4=0
$$

$$
x=0, x=2, x=dfrac{4}{3} text{or} x=dfrac{4}{3}
$$

Note that there are two similar solutions $color{#4257b2}x=dfrac{4}{3}$, so we can write it just once.

So the solutions of the equation are $color{#c34632}x=0, x=2 {color{Black}text{or}} x=dfrac{4}{3}$.

(c) We need to solve the equation $color{#4257b2}6x^{4}-13x^{3}-29x^{2}+52x=-20$. First, we can add $color{#4257b2}20$ to each side to make the right side equals zero.

$$
6x^{4}-13x^{3}-29x^{2}+52x=-20
$$

$$
6x^{4}-13x^{3}-29x^{2}+52x+20=0
$$

Now we can let $color{#4257b2}f(x)=6x^{4}-13x^{3}-29x^{2}+52x+20$ and then use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=6x^{4}-13x^{3}-29x^{2}+52x+20$, so
$color{#4257b2}p=20$ and $color{#4257b2}q=6$. As a result the root could be of the form $color{#4257b2}dfrac{20}{6}$ and the factors of it are $color{#4257b2}pm 1, pm 2, pm 4, pm 5, pm 10, pm 20, pm dfrac{1}{2}, pm dfrac{5}{2}, pm dfrac{1}{3}, pm dfrac{2}{3}, pm dfrac{4}{3}, pm dfrac{5}{3}, pm dfrac{10}{3}, pm dfrac{20}{3}, pm dfrac{1}{6}, pm dfrac{5}{6}$.

Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=6x^{4}-13x^{3}-29x^{2}+52x+20
$$

$$
f(1)=6(1)^{4}-13(1)^{3}-29(1)^{2}+52(1)+20=36
$$

$$
f(-1)=6(-1)^{4}-13(-1)^{3}-29(-1)^{2}+52(-1)+20=-42
$$

$$
f(1)=6(2)^{4}-13(2)^{3}-29(2)^{2}+52(2)+20=0
$$

By the factor theorem, $color{#4257b2}(x-2)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x-2)$ to find the remaining factors.

$$
polylongdiv{6x^{4}-13x^{3}-29x^{2}+52x+20}{x-2}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x-2right)left(6x^{3}-x^{2}-31x-10right) (1)$. Now we note that we have a cubic function, so we can use the factor theorem one more time to find another factor but this once for the cubic function $color{#4257b2}y(x)=6x^{3}-x^{2}-31x-10$. Note that we let $color{#4257b2}f(x)=(x-2) [y(x)]$

$$
y(x)=6x^{3}-x^{2}-31x-10
$$

$$
y(1)=6(1)^{3}-(1)^{2}-31(1)-10=-36
$$

$$
y(-1)=6(-1)^{3}-(-1)^{2}-31(-1)-10=14
$$

$$
y(2)=6(2)^{3}-(2)^{2}-31(2)-10=-28
$$

$$
y(-2)=6(-2)^{3}-(-2)^{2}-31(-2)-10=0
$$

By the factor theorem, $color{#4257b2}(x+2)$ is a factor of the function $color{#4257b2}y(x)$. Now we can divide the function $color{#4257b2}y(x)$ by the factor term $color{#4257b2}(x+2)$ to find the remaining factors.

$$
polylongdiv{6x^{3}-x^{2}-31x-10}{x+2}
$$

So the function $color{#4257b2}y$ can be rewrite as $color{#4257b2}y(x)=left(x+2right)left(6x^{2}-13x-5right)$. Now the next step is to factor the quadratic function $color{#4257b2}6x^{2}-13x-5$.

$$
y(x)=left(x+2right)left(6x^{2}-13x-5right)
$$

$$
y(x)=left(x+2right)left(3x+1right)left(2x-5right)
$$

Now we can substitute the function $color{#4257b2}y$ in the function (1) for $color{#4257b2}f(x)$ to find the factors of the function $color{#4257b2}$.

$$
f(x)=f(x)=left(x-2right)left(6x^{3}-x^{2}-31x-10right)
$$

$$
f(x)=left(x-2right)left(x+2right)left(3x+1right)left(2x-5right)
$$

Now we found the factors of the function
$color{#4257b2}f(x)=6x^{4}-13x^{3}-29x^{2}+52x+20=0$, so we can substitute in our equation to find the solutions of it.

$$
6x^{4}-13x^{3}-29x^{2}+52x+20=0
$$

$$
(x-2)(x+2)(3x+1)(2x-5)=0
$$

Now we can use the zero-factor property.

$$
x-2=0, x+2=0, 3x+1=0 text{or} 2x-5=0
$$

$$
x=2, x=-2, x=-dfrac{1}{3} text{or} x=dfrac{5}{2}
$$

So the solutions of the equation are $color{#c34632}x=-2, x=-dfrac{1}{3}, x=2 {color{Black}text{or}} x=dfrac{5}{2}$.

(d) We need to solve the equation $color{#4257b2}x^{4}-6x^{3}+10x^{2}-2x=x^{2}-2x$. First, we can subtract $color{#4257b2}x^{2}-2x$ from each side to make the right side equals zero.

$$
x^{4}-6x^{3}+10x^{2}-2x=x^{2}-2x
$$

$$
x^{4}-6x^{3}+10x^{2}-2x-x^{2}+2x=0
$$

$$
x^{4}-6x^{3}+10x^{2}cancel{-2x}-x^{2}cancel{+2x}=0
$$

$$
x^{4}-6x^{3}+9x^{2}=0
$$

Now we note that all terms of the function contain $color{#4257b2}x^{2}$, so we can take it as a common factor.

$$
x^{2}left(x^{2}-6x+9right)=0
$$

Now the next step is to factor the quadratic function $color{#4257b2}x^{2}-6x+9$.

$$
x^{2}left(x-3right)left(x-3right)=0
$$

Now we can use the zero-factor property.

$$
x^{2}=0, x-3=0 text{or} x-3=0
$$

$$
x=0, x=3 text{or} x=3
$$

Note that we have four roots but each two roots are similar where there are two roots equal zero and the two other roots equals $color{#4257b2}3$, so we can write each of them just once.

So the solutions of the equation are $color{#c34632}x=0 {color{Black}text{or}} x=3$

Large{$text{color{Brown}(a) $x=-2, x=3 {color{Black}text{or}} x=5$
\
\
(b) $x=0, x=2 {color{Black}text{or}} x=dfrac{4}{3}$
\
\
(c) $x=-2, x=-dfrac{1}{3}, x=2 {color{Black}text{or}} x=dfrac{5}{2}$
\
\
(d) $x=0 {color{Black}text{or}} x=3$}$

The volume of a box is a product of its length, width, and height. Hence, for the given box the volume is

$$
V=(30-2x)(20-2x)x.tag{1}
$$

Note that the second term suggests that the values of $x$ can not be greater than $10$, because otherwise, we could not make that side of the box. Hence

$$
xle10.tag{2}
$$

Since the volume of the box is given, we could make an equation and solve for $x$.

Equate the Eq. $(1)$ with $1008$. We obtain

$$
begin{align*}
(30-2x)(20-2x)x&=1008\
(600-100x+4x^2)x&=1008\
4x^3-100x^2+600x-1008&=0\
x^3-25x^2+150x-252&=0
end{align*}
$$

The last equation we can solve using the Factoring Theorem. It states that $x-a$ is a factor of $f(x)$ if and only if $f(a)=0$.

Note that the factors of $252$ are $pm1,pm2,pm3,pm4,pm6,pm9$. We won’t consider other factors of $252$, because of the condition given by Eq. $(2)$. We will substitute these values instead of $x$ until we obtain one solution that is equal to zero, as follows:

$$
begin{align*}
f(1)&=1^3-25cdot1^2+150cdot1-252=-126\
f(2)&=2^3-25cdot2^2+150cdot2-252=-44\
f(3)&=3^3-25cdot3^2+150cdot3-252=0
end{align*}
$$

Hence, $x-3$ is a factor of $x^3-25x^2+150x-252$, and $x=3$ is one possible solution. Other solution we will find by using long division to lower the degree of a polynomial, which will give a quadratic equation.

Dividing $x^3-25x^2+150x-252$ by $x-3$, we obtain:

$$
begin{align*}
phantom{x}x^2-22x+84phantom{bb}\
x-3overline{smash{big)}x^3-25x^2+150x-252}\
underline{-(x^3-3x^2)phantom{-bbbbbbbbbb)}}\
-22x^2+150x-252\
underline{phantom{..}-(-22x^2+66x)phantom{aaa…..}}\
84x-252\
underline{phantom{……………………}84x-252}\
0
end{align*}
$$

Now we need to solve $x^2-22x+84=0$. Note that this is the quadratic equation.

Quadratic equation $ax^2+bx+c=0$ qcan be solved using the quadratic formula

$$
x_{1,2}=dfrac{-bpmsqrt{b^2-4ac}}{2a}
$$

In our equation we have that $a=1$, $b=-22$ and $c=84$. Substituting these values in quadratic formula, we obtain:

$$
begin{align*}
x_{1,2}&=dfrac{-(-22)pmsqrt{(-22)^2-4cdot1cdot84}}{2cdot1}\
&=dfrac{22pmsqrt{484-336}}{2}\
&=dfrac{22pmsqrt{148}}{2}\
&=dfrac{22pmsqrt{4cdot37}}{2}\
&=dfrac{22pm2sqrt{37}}{2}\
&=11pmsqrt{37}\
x_1&=11-sqrt{37}approx4.92\
x_2&=11+sqrt{37}approx17.
end{align*}
$$

Note that solution $x_2$ does not satisfy the condition given in Eq. $(2)$. Hence, only possible solutions are $x=3$ or $x=4.92$.

$x=3$ or $x=4.92$

Mayas score can be modeled by $S(x)=x(x-4)(x-6)$ where, $x$ represent the number of game, abswer for the following question.

$$
text{color{#4257b2}(a) after which game was score equal to zero?}
$$

$$
S(x)=x(x-4)(x-6)=0
$$

Use zero property as follows:

$$
x=0 x-4=0 x-6=0
$$

$$
x=0 x=4 x=6
$$

$$
text{color{#4257b2}(b) after which game was score equal to $-5$?}
$$

$$
S(x)=x(x-4)(x-6)=-5
$$

Use zero property as follows:

$$
x=-5 x-4=-5 x-6=-5
$$

$$
x=-5 x=-1 x=1
$$

$$
text{color{#4257b2}(c) after which game was score equal to 16?}
$$

$$
S(x)=x(x-4)(x-6)=16
$$

Use zero property as follows:

$$
x=16 x-4=16 x-6=16
$$

$$
x=16 x=20 x=22
$$

$$
text{color{#4257b2}(d) Draw sketch for $S(x)$}
$$

The sketch is not represent a score of Mayas due to the graph is sketched when the game score was equal zero

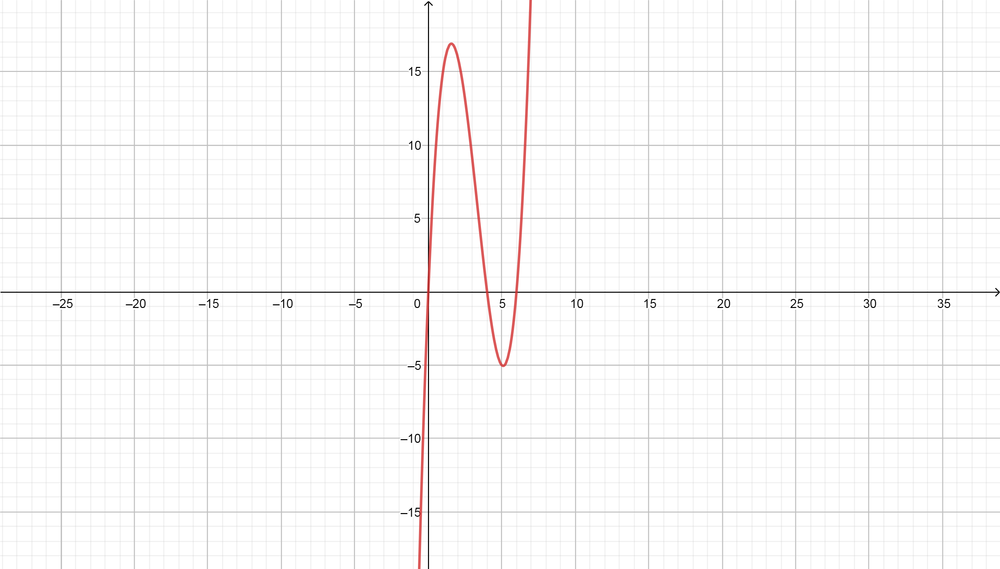
$$
text{color{Brown}(a) $x=0 x=4 x=6$
\ \
(b) $x=-5 x=-1 x=1$
\ \
(c) $x=16 x=20 x=22$
\ \
(d) The sketch is not represent a score of Mayas due to the graph is sketched when the game score was equal zero.}
$$

$$
text{color{#4257b2}The function of $S(t)=-dfrac{1}{2} g t^2+V_{o} t+S_{o}$, where $(S)$, represent the height above the planet surface, m, $(g)$ the acceleration due to the gravity, m/s$^2$, $(V_{o})$, the initial velocity, m/s, $(t)$, time in second and $(S_{o})$, the initial height, m
\ \
How long it takes an object to hit the surface of Mars if the object dropped from $(1000)$ m above the surface, where, $(g=-3.92)$ m/s$^2$.}
$$

$$
S(t)=-dfrac{1}{2} g t^2+V_{o} t+S_{o}
$$

When the object hit the surface of Mars, the initial height and initial velocity is equal zero, so the function will be as follows:

$$
S(t)=-dfrac{1}{2} g t^2
$$

$$
1000=-dfrac{1}{2} cdot -3.92 cdot t^2 1000=1.96 t^2
$$

Divide both of sides by $(1.96)$ as follows:

$$
t^2=dfrac{1000}{1.96} t^2=510.205
$$

Use square root property as follows:

$$
sqrt{t^2}=sqrt{510.205} t=pm 22.587 text{second}
$$

Not reality the time will be negative value, so the correct answer is equal, $(22.587)$ second.

The object need $(22.587)$ second to hit the surface of Mars

$$
text{color{Brown}The object need $(22.587)$ second to hit the surface of Mars}
$$

The distance of the chip from its harbour is modelled by the function of $d(t)=-3t^3+3t^2+18t$ where $(t)$ is time elapsed in hour since diparture from the harbour. Answer for the following questions.

$$
text{color{#4257b2}(a) Factor the time function}
$$

$$
d(t)=-3t^3+3t^2+18t
$$

Find the GCF as follows:

$$
d(t)=t[-3t^2+36+18) d(t)=t[(3t+6)(-t+3)]
$$

$$
text{color{#4257b2}(b) When does the ship return to the harbour?}
$$

$$
d(t)=t[(3t+6)(-t+3)]
$$

Use zero property as follows:

$$
t=0
$$

$$
3t+6=0 3t=-6 t=-2
$$

$$
-t+3=0 t=3
$$

After $(6)$ hours from the begin the chip will return to its harbour.

$$
text{color{#4257b2}(c) There is another zero of $d(t)$ what is it? and why is not relevant to the equation}
$$

The another time is equal $(-2)$, and its not relevant to the problem due to it has a negative sign and its not reality the time be a negative value.

$$
text{color{#4257b2}(d) Draw a sketch of the function, where, $0le tle3$}
$$

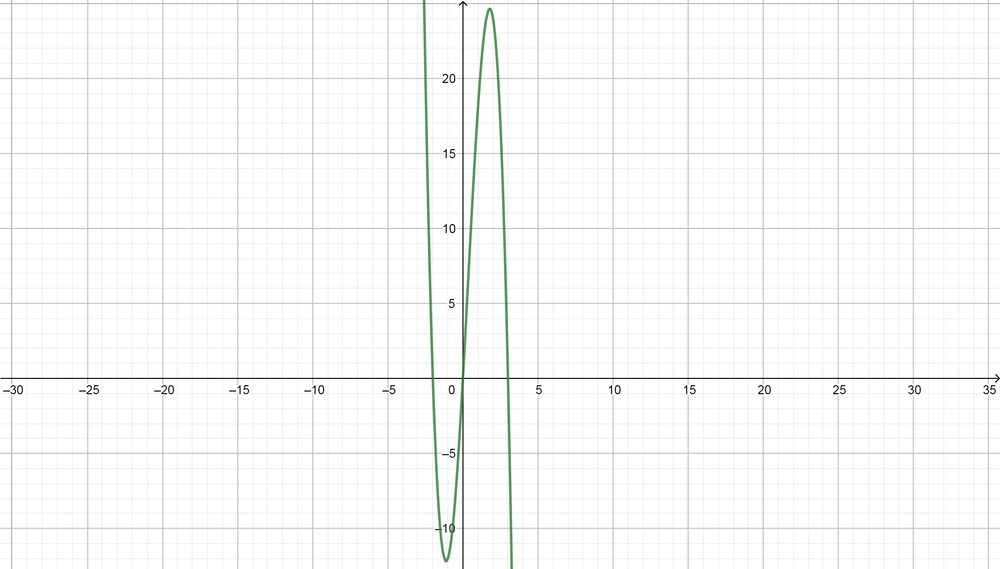
$$
text{color{#4257b2}(e) Estimate the time that the ship begin return back to the harbour}
$$

The time needed is $(3)$ hours to begin return back to its harbour

$$
text{color{Brown}(a) $d(t)=t[(3t+6)(-t+3)]$
\ \
(b) After $(6)$ hours from the begin the chip will return to its harbour.
\ \
(c) The another time is equal $(-2)$, and its not relevant to the problem due to it has a negative sign and its not reality the time be a negative value.
\ \
(d) See the graph.
\ \
(e) $(3)$ hours.}
$$

The volume of air in a person’s lungs can be represented by $V(t)=0.027t^3-0.27t^2+0.975t$, where volume, $(V)$ measured in litter at time $(t)$ in second.

$$
text{color{#4257b2}(a) What restriction must be placed on $(t)$?}
$$

Use GCF as follows:

$$
V(t)=0.027 t left[t^2-10 t+25right] V(t)=0.027 t left[(t-5)^2right]
$$

Use zero property as follows:

$$
0.027 t=0 t=0 text{second}
$$

$$
t-5=0 t=5 text{second}
$$

$$
text{color{#4257b2}(b) How many second passed if the volume of air is equal $(0.25)$ L?}
$$

$$
V(t)=0.027 t [t^2-10 t+25]
$$

Substitute the value of volume of air as $(V(t)=0.25)$ as follows:

$$
0.25=0.027 t left[(t-5)^2right]
$$

Use zero property as follows:

$$
0.027 t=0.25 t=dfrac{0.25}{0.027} t=9.259 text{second}
$$

$$
t-5=0.25 t=5+0.25 t=5.25 text{second}
$$

$$
text{color{Brown}(a) $t=0 text{second} t=5 text{second}$
\ \
(b) $t=9.259 text{second} t=5.25 text{second}$}
$$

Why the following expression has a no real solution.

$$
color{#4257b2}0=5x^8+10x^6+7x^4+18x^2+132
$$

Because the $y$ intercept has a large number and then it’s not across with $x$ axis to get zeros to solve it.

$$
text{color{Brown}Because the $y$ intercept has a large number and then it’s not across with $x$ axis to get zeros to solve it.}
$$

Determine algebraically where the cubic function that has zeros $2, 3, -5$ and pass through point $(4, 36)$ has a value of $120$

According the standard formula for cubic function as follows:

$$
y=a(x+x_{1})+(x+x_{2})+(x+x_{2})
$$

$$
y=a(x-2)(x-3)(x+5) 36=a[(4-2)(4-3)(4+5)]
$$

$$
36=18 a a=2
$$

$$
y=2(x-2)(x-3)(x+5)
$$

At value of function equal $y=120$

$$
120=2(x-2)(x-3)(x+5) 60=(x-2)(x-3)(x+5)
$$

Use distributive property as follows:

$$
60=(x^2-5x+6)(x+5) 60=x^3-5x^2+6x+5x^2-25x+30
$$

$$
60=x^3-19x+30 x^3-19x=60-30
$$

Use GFC as follows:

$$
x(x^2-19)=30
$$

Use equal property as follows:

$$
x^2=30+19 x^2=49
$$

Use square root property as follows:

$$
sqrt{x^2}=sqrt{49} x=pm7
$$

The cubic function has a value of $120$ at the value of $x=pm7$

$$
text{color{Brown}The cubic function has a value of $120$ at the value of $x=pm7$}
$$

For each strategy below create the cubic or quartic equation you might solve by using that strategy

$$
text{color{#4257b2}(a) Factor theorem}
$$

$$
f(x)=4x^3-12x^2-x+3 (x-3) text{is a factor of the function}
$$

$$
text{color{#4257b2}(b) Common factor}
$$

$$
f(x)=3x^3-3x^2-18x f(x)=x(3x^2-3x-18)
$$

$$
text{color{#4257b2}(c) Factor by groping}
$$

$$
f(x)=4x^3-12x^2-x+3 f(x)=4x^2(x-3)-1(x-3)
$$

$$
text{color{#4257b2}(d) Quadratic formula}
$$

$$
=3x^3-5x^2-7x=0 x[3x^2-5x-7]=0
$$

$$
text{color{#4257b2}(e) Difference or sum of cubes}
$$

$$
f(x)=x^3-8=(x-2)^3 f(x)=(x-2)(x^2+2x+4)
$$

$$
text{color{#4257b2}(f) Graphing technology}
$$

$$
f(x)=x^3-7x+6
$$

$$
text{color{Brown}(a) $f(x)=4x^3-12x^2-x+3$ (b) $f(x)=3x^3-3x^2-18x$
\ \
(c) $f(x)=4x^3-12x^2-x+3$ (d) $3x^3-5x^2-7x=0$
\ \
(e) $f(x)=x^3-8=(x-2)^3$ (f) $f(x)=x^3-7x+6$}
$$

$$
text{color{#4257b2}(a) Its possible that the equation of polynomial degree of $(4)$ can have no real roots, create one represent this case and explain why it can’t have any real roots?}
$$

There are functions that have a degree of $(4)$ and not have real roots such the following equation:

$$
f(x)=(x^2+4)^2
$$

This equation has no any real roots because when we use zero property to get the real roots, we get the negative value in the other side and not really get root to the negative value, so this type of equation has no real roots.

$$
text{color{#4257b2}(b) Explain, why a degree of $(5)$ polynomial equation must have at least one real root?}
$$

Because the polynomial degree that has a power of $(5)$ represented by the following terms:

** Multiply quartic function by linear function.

** Multiply quadratic function by cubic function.

** Multiply doubled quadratic function by linear function.

$$
text{color{Brown}(a) $f(x)=(x^2+4)^2$
\ \
This equation has no any real roots because when we use zero property to get the real roots, we get the negative value in the other side and not really get root to the negative value, so this type of equation has no real roots.
\ \
(b) Because the polynomial degree that has a power of $(5)$ represented by the following terms:
\ \
** Multiply quartic function by linear function.
\ \
** Multiply quadratic function by cubic function.
\ \
** Multiply doubled quadratic function by linear function.}
$$

$$
text{color{#4257b2}The factor theorem only deal with rational zeros, create a degree $(5)$ of polynomial that have no rational zeros, and explain why it has no rational zeros?}
$$

When the function has a rational zeros, that mean there is areal number value of $(x)$ substitute in the function to be equal zero.

$$
x^5+x^4-5x^3+x^2-6x+12=0
$$

Let use value of $(x-1)$ as a factor of the function and use theorem property as follows:

$$
1 | 1 1 -5 1 -6 12
$$

$$
1 2 -3 -2 -8
$$

$$
1 2 -3 -2 -8 4
$$

$$
x^5+x^4-5x^3+x^2-6x+12=(x-1)(x^4+2x^3-3x^2-2x-8)+4
$$

The remainder for this dividing operation is equal $(4)$, and its not equal zero, so this function has no rational roots.

Value of $(x-1)$, called divisor

Value of $(x^4+2x^3-3x^2-2x-8)$, called quotient.

This function has no rational zeros because there are no real number substituted in the function to get the value of $f(x)$ be zero.

$$
text{color{Brown}$$x^5+x^4-5x^3+x^2-6x+12=0$$
\
This function has no rational zeros because there are no real number substituted in the function to get the value of $f(x)$ be zero.}
$$