Since $sin theta+cos(theta-dfrac{pi}{2})$, we have:

$sin dfrac{2pi}{5}=cos(dfrac{2pi}{5}-dfrac{pi}{2})=cos(dfrac{4pi}{10}-dfrac{5pi}{10})=cos(-dfrac{pi}{10})$

Since $cos theta=cos(2pi-theta)$, we have:

$cos(-dfrac{pi}{10})=cos(2pi-(-dfrac{pi}{10}))=cos(2pi+dfrac{pi}{10})$.

Since the period of the cosine function is $2pi$, we have that:

$cos(2pi+dfrac{pi}{10})=cos dfrac{pi}{10}$.

Therefore, $textbf{answer (a) is correct}$.

Also, since $cos(pi-theta)=-cos theta$, we have:

$cos dfrac{pi}{10}=-cos(pi-dfrac{pi}{10})=-cos(dfrac{10pi}{10}-dfrac{pi}{10})=-cos dfrac{9pi}{10}$.

Therefore, $textbf{answer (c) is correct}$.

Also, since $sin(pi-theta)=sin theta$, we have:

$sin dfrac{2pi}{5}=sin(pi-dfrac{2pi}{5})=sin(dfrac{5pi}{5}-dfrac{2pi}{5})=sin dfrac{3pi}{5}$.

Therefore, $textbf{answer (b) is correct.}$

Since answers (a), (b) and (c) are all correct, $textbf{the correct answer is $(d)$}$.

Since $cos(a-b)=cos a cos b + sin a sin b$, we have:

$cos dfrac{pi}{12}=cos(dfrac{4 pi}{12}-dfrac{3 pi}{12})=cos(dfrac{pi}{3}-dfrac{pi}{4})$=

$cos dfrac{pi}{3} cos dfrac{pi}{4}+sin dfrac{pi}{3} sin dfrac{pi}{4}=(dfrac{1}{2})(dfrac{sqrt{2}}{2})+(dfrac{sqrt{3}}{2})(dfrac{sqrt{2}}{2})=dfrac{sqrt{2}}{4}+dfrac{sqrt{6}}{4}=dfrac{sqrt{2}+sqrt{6}}{4}$.

So, $textbf{the answer is}$ (b).

Since $sin alpha=dfrac{12}{13}$, the leg opposite the angle $alpha$ in a right triangle has a length of $12$, while the hypotenuse of the right triangle has a length of $13$. For this reason, the other leg of the right triangle can be calculated as follows:

$x^2+12^2=13^2$

$x^2+144=169$

$x^2+144-144=169-144$

$x^2=25$

$x=5$

Since $tan alpha=dfrac{opposite leg}{adjacent leg}$,$tan alpha=dfrac{12}{5}$.In addition, $sin beta=dfrac{8}{17}$, the leg opposite the angle $beta$ in a right triangle has a length of $8$, while the hypotenuse of the right triangle has a length of $17$. For this reason, the other leg of the right triangle can be calculated as follows:

$x^2+8^2=17^2$

$x^2+64=289$

$x^2+64-64=289-64$

$x^2=225$

$$
x=15
$$

Since $tan beta=dfrac{opposite leg}{adjacent leg}$,$tan beta=dfrac{8}{15}$.

Since $tan(a+b)=dfrac{tan a+ tan b}{1-tan a tan b}$,

$tan( alpha+beta)=dfrac{tan alpha+tan beta}{1-tan alpha tan beta}=$

$=dfrac{dfrac{12}{5}+dfrac{8}{15}}{1-(dfrac{12}{5})(dfrac{8}{15})}$

$=dfrac{dfrac{36}{15}+dfrac{8}{15}}{1-dfrac{96}{75}}$

$=dfrac{dfrac{44}{15}}{dfrac{75}{75}-dfrac{96}{75}}$

$=dfrac{dfrac{44}{15}}{-dfrac{21}{75}}$

$=dfrac{44}{15}timesleft( -dfrac{75}{21}right)$

$=-dfrac{3300}{315}$

$=-dfrac{220}{21}$

$textbf{Therefore, the correct answer is $a)$}$

Since $sin theta=dfrac{3}{8}$, the leg opposite the angle $theta$ in a right triangle has a length of $3$, while the hypotenuse of the right triangle has a length of $8$. For this reason, the other leg of the right triangle can be calculated as follows:

$x^2+3^2=8^2$

$x^2+9=64$

$x^2=55$

$x=sqrt{55}$

Since $tan theta=dfrac{opposite leg}{adjacent leg}$, we have that:

$tan theta=-dfrac{3}{sqrt{55}}=-dfrac{3sqrt{55}}{55}$

Since $tan 2theta=dfrac{2tan theta}{1-tan^2 theta}$, we have:

$tan 2theta=dfrac{2(-dfrac{3sqrt{55}}{55})}{1-(-dfrac{3sqrt{55}}{55})^2}=dfrac{-dfrac{6sqrt{55}}{55}}{dfrac{2530}{3025}}=-dfrac{3sqrt{55}}{23}$.

Therefore, $textbf{the correct answer is (a)}$.

Note that we can write
$$
2cdot dfrac{pi}{8}=dfrac{pi}{4},$$
and we know that $cos frac{pi}{4}=frac{sqrt{2}}{2}$, which we can use to compute the cosine function of an angle $frac{pi}{8}$.

The cosine function of a double angle is
$$
cos(2theta)=cos^2theta-sin^2theta.$$
Using the Pythagorean Identity $cos^2theta+sin^2theta=1$ we can substitute $sin^2theta=1-cos^2theta$ in the equation above, and obtain the equation with only the cosine function. Hence, we obtain:
$$
begin{align*}
cos(2theta)&=cos^2theta-(1-cos^2theta)\
&=cos^2theta-1+cos^2theta\
&=2cos^2theta-1.quadquad(1)
end{align*}$$

Now using Eq. $(1)$ we can write
$$
cos dfrac{pi}{4}=cosleft(2cdotdfrac{pi}{8} right)=2cos^2dfrac{pi}{8}-1.$$
Substituting the value $cos frac{pi}{4}=frac{sqrt{2}}{2}$ in this equation and adding $1$ throughout, we obtain:
$$
begin{align*}
2cos^2dfrac{pi}{8}&=dfrac{sqrt{2}}{2}+1&&text{[Simplify]}\
2cos^2dfrac{pi}{8}&=dfrac{sqrt{2}+2}{2}&&text{[Divide by $2$ throughout]}\
cos^2dfrac{pi}{8}&=dfrac{2+sqrt{2}}{4}&&text{[Find square root on both sides]}\
cosdfrac{pi}{8}&=sqrt{dfrac{2+sqrt{2}}{4}}\
cosdfrac{pi}{8}&=dfrac{sqrt{2+sqrt{2}}}{2}.
end{align*}$$
Hence, the exact value of the given function is given as an answer *(d)*.

The expression $dfrac{2-sec^2(dfrac{1}{2}x)}{sec^2(dfrac{1}{2}x)}$ can be simplified as follows:

$dfrac{2-sec^2(dfrac{1}{2}x)}{sec^2(dfrac{1}{2}x)}=dfrac{2}{sec^2(dfrac{1}{2}x)}-dfrac{sec^2(dfrac{1}{2}x)}{sec^2(dfrac{1}{2}x)}$

$=2 cos^2left(dfrac{1}{2}x right)-1$

Since $cos 2theta=2cos^2theta-1$,

$2cos^2left(dfrac{1}{2}x right)-1= cos 2left(dfrac{1}{2}x right)=cos x$

Therefore,the correct answer is $c)$.

The identity $dfrac{2 tan x}{1+ tan^2x}=sin2x$ can be proven as follows:

$dfrac{2 tan x}{1+ tan^2 x}=dfrac{2dfrac{sin x}{cos}}{sec^2 x}$

$=2dfrac{sin x}{cos x}times cos^2x$

$=2 sin x cos x$

$=sin 2x$

The identities $1+tan^2x=sec^2x$, $sin 2x=2sin x cos x$, and $tan x=dfrac{sin x}{cos x}$ were all used in the proof.

$textbf{Therefore, the correct answer is d) }$.

The equation $5+7 sintheta=0$ can be solved as follows:

$5+7 sin theta= 0$

$5+7 sin theta-5=0-5$

$7 sin theta=-5$

$dfrac{7 sin theta}{7}=-dfrac{5}{7}$

$sin theta=-dfrac{5}{7}$

$-sin^{-1}(sin theta)=sin^{-1}left(-dfrac{5}{7} right)$

$theta=sin^{-1}left(-dfrac{5}{7} right)$

$theta=-0.80$ or $-2.35$

$textbf{Therefore, the correct answer is b)}$.

The blade tip is at least $30m$ above the ground when $18 cosleft(pi t+dfrac{pi}{4} right)+23geq 30$.This inequality can be simplified as follows:

$18cosleft(pi t+dfrac{pi}{4} right)+23geq30$

$18cosleft(pi t+dfrac{pi}{4} right)+23-30geq30-30$

$18cosleft(pi t +dfrac{pi}{4} right)-7geq 0$

The inequality $18cosleft(pi t +dfrac{pi}{4} right)-7geq0$ can be solved

by graphing the function $h(t)=18cosleft(pi t +dfrac{pi}{4} right)-7$ determining where the graph is at or above the $x-axis$.

The graph is as follows:

The graph is at or above the $x$-axis in the inetrvals $1.37leq xleq2.12, 3.37leq x leq 4.12$ and $5.37leq x leq 6.12$. Therefore, the correct answer is $c)$

The equation $(2sin x +1)(cos x-1)=0$ is true when either $2sin x+1=0$ or $cos x-1=0$(or both). If $2 sin x+1=0$,$x$ can be solved for as follows:

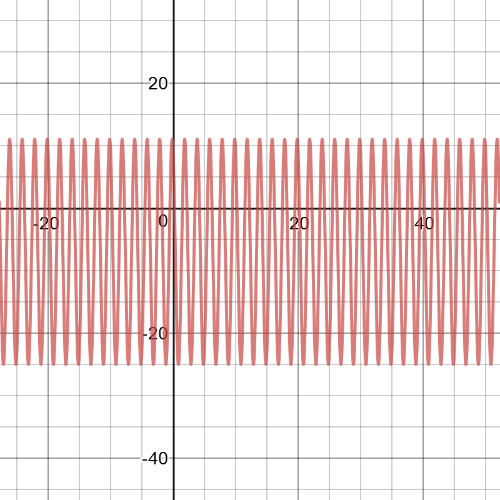
$2sin x +1=0$

$2sin x+1-1=0-1$

$2 sin x=-1$

$dfrac{2 sin x}{2}=-dfrac{1}{2}$

$sin x=-dfrac{1}{2}$

The solutions to the equation $sin x=-dfrac{1}{2}$ occur at $x=210^o$ or $330^o$.

If $cos x-1=0,$ $x$ can be solved for as follows:

$cos x-1=0$

$cos x-1+1=0+1$

$cos x=1$

The solutions to the equation $cos x=1$ occur at $x=0^o$ or $360^o$. Therefore, the correct answer is $d)$.

Since the solutions to the equation are $theta=0$, $dfrac{pi}{3}, dfrac{5 pi}{3}$, or $2pi$, either $costheta=1$ or $costheta=dfrac{1}{2}$.

(This is because $cos0=1, cosdfrac{pi}{3}=dfrac{1}{2}, cosdfrac{5pi}{3}=dfrac{1}{2},$ and $cos2pi=1$). For this reason,either $costheta-1=0$ or $costheta-dfrac{1}{2}=0$(or both). If the left sides of these two equations are considert factors of a quadratic equation and multiplied together, the result is as follows:

$(costheta-1)left(costheta-dfrac{1}{2} right)=0$

$cos^2theta-costheta-dfrac{1}{2}costheta+dfrac{1}{2}=0$

$cos^2theta-dfrac{3}{2}costheta+dfrac{1}{2}=0$

If both sides of the equation are multiplied by $2$, the result is as follows:

$(2)left(cos^2theta-dfrac{3}{2}costheta+dfrac{1}{2} right)=(2)(0)$

$2cos^2theta-3costheta+1=0$

Since $2cos^2theta-1=cos2theta$, the equation can be rewritten as follows:

$2cos^2theta-1+1-3 costheta+1=0$

$cos2 theta+1-3costheta+1=0$

$cos2theta-3costheta+2=0$

$textbf{Therefore, the correct answer is a)}$.

In the equation $y=log_{7}x,y$ is the power to which $7$ must be raised in order to produce $x$.

Therefore,the exponential form of $y=log_{7}x$ is $x=7^y$, and the correct answer is $b)$.

In logarithmic functions of the form $f(x)=a log_{10}left[ k(x-d)right]+c$, if
$a$ is negative, $f(x)$ is reflected in the
$x$-axis. Also, if $0<|k|<1$, a horizontal stretch of factor $left| dfrac{1}
{k}right|$ occurs, and if $f(x)=log_{10}x$ a vertical translation of $c$ units
up occurs. Therefore, if $b=1.0117$ is reflected in the $x$-axis, stretched
horizontally by a factor of $3$, and translated $2$ units up, the resulting
function is $f(x)=-log_{10}left(dfrac{1}{3}x right)+2$, and $textbf{the
correct answer is d)}$.

Since the value of $log_{7}49$ is the power to which $7$ must be raised to produced $49$, $log_{7}49=2$.
Therefore, $7^{log_{7}49}=7^2=49$, so $textbf{the correct answer is d).}$

The lenth of the palnet’s year in days can be calculated as follows:

$log_{10}T=1.5log_{10}d-0.45$

$log_{10}T=1.5log_{10}11-0.45$

$log_{10}T=log_{10}11^{1.5}-0.45$

$log_{10}T-log_{10}11^{1.5}=log_{10}11^{1.5}-0.45-log_{10}11^{1.5}$

$log_{10}T-log_{10}11^{1.5}=-0.45$

$log_{10}dfrac{T}{11^{1.5}}=-0.45$

$10^{-0.45}=dfrac{T}{11^{1.5}}$

$10^{-0.45}times 11^{1.5}=dfrac{T}{11^{1.5}}times 11^{1.5}$

$T=10^{-0.45}times 11^{1.5}$

$T=0.3548times 36.4829$

$T=12.9$

Therefore, $textbf{the correct answer is c).}$

The equation $log_{4}x+3=log_{4}1024$ can be solved as follows:

$log_{4}x+3=log_{4}1024$

$log_{4}x+3-log_{4}x=log_{4}1024-log_{4}x$

$log_{4}1024-log_{4}x=3$

$log_{4}dfrac{1024}{x}=3$

$4^3=dfrac{1024}{x}$

$64=dfrac{1024}{x}$

$64times x=dfrac{1024}{x}times x$

$64x=1024$

$dfrac{64x}{64}=dfrac{1024}{64}$

$x=16$

$textbf{Therefore, the correct answer is a)}$.

$log_{5}25x=log_{5}25+log_{5}x=2+log_{5}x$

So $g(x)$ is a vertical translation of $f(x)$ $2$ units up, and the correct answer is b).

The equation $x=log_{3}27sqrt{3}$ can be rewritten as $3^x=27sqrt{3}$. Since $27=3^3$ and $sqrt{3}=3^{1/2}$, the equation $3^x=27sqrt{3}$ can be rewritten as $3^x=3^3times 3^{1/2}$. By adding the exponents on the right side of the equation, the equation becomes $3^x=3^{3^{1/2}}$. Therefore, $textbf{$x$ must be equal $3dfrac{1}{2}$, and the correct answer is b)}$.

Since the formula for compound interest is $A=P(1+i)^n$, the lenth of time it will take for the investment to be worth more than
$$
6400$ can be calculated as follows:

$6400<1600(1+0.01)^n$\

$dfrac{6400}{1600}<dfrac{1600(1+0.01)^n}{1600}$\

$4<(1+0.01)^n$ \

$log_{10}4<log_{10}((1+0.01)^n)$\

$log_{10}4dfrac{log_{10}4}{log_{10}(1+0.01)}$\

$n>dfrac{log_{10}4}{log_{10}1.01}$\

$n>dfrac{0.6021}{0.0043}$\

$n>140$\

Since $n$ represents the number of months it will take for the investment to be worth more than $ $6400$, and since there are $12$ months in a year, the number of years it will take for the investment to be worth more than $ $6400$ is $11$ years and $8$ months. Therefore, the correct answer is $c)$.
$$

Since the formula for the loudness of sound is $L=10logleft(dfrac{I}{I_{0}} right)$ , the intensity of the soundofa jet taking off with a loudness od $133$dB can be calculated as follows:

$133=10logleft(dfrac{I}{10^{-12}} right)$

$dfrac{133}{10}=dfrac{10logleft(dfrac{I}{10^{-12}} right)}{10}$

$dfrac{133}{10}=logleft(dfrac{I}{10^{-12}} right)$

$10^{dfrac{133}{10}}=dfrac{I}{10^{-12}}$

$10^{13.3}=dfrac{I}{10^{-12}}$

$10^{13.3}times 10 ^{-12}=dfrac{I}{10^{-12}}times 10^{-12}$

$I=10^{1.3}$

$I=20.0$ $W/m^2$

Therefore, $textbf{the correct answer is d)}$.

The equation $log_{a}(x-3)+log_{a}(x-2)=log_{a}(5x-15)$ can be rewritten as follows:
$log_a(x-3)+log_a(x-2)=log_a(5x-15)$

$log_{a}(x-3)(x-2)=log_{a}(5x-15)$

For this reason, $(x-3)(x-2)=5x-15.$ This equation can be solved as follows:

$(x-3)(x-2)=5x-15$

$x^2-3x-2x+6=5x-15$

$x^2-5x+6=5x-15$

$x^2-5x+6-5x+15=5x-15-5x+15$

$x^2-10x+21=0$

$(x-7)(x-3)=0$

$x=7$ or $x=3$

Since it’s impossible to find the $log$ of $0$, $x=3$ is not a valid answer, because if $3$ is substitued back into the original equation, both sides of the equation would have a term of $log_{a}0$. Therefore, the correct answer is $b)$.

Since Carbon $14$ has a half-life of $5730$ years, the following equation holds true:

$0.017=(3.9)left(dfrac{1}{2} right)^{dfrac{x}{5730}}$

This equation can be solved as follows:

$0.017=(3.9)left(dfrac{1}{2} right)^{dfrac{x}{5730}}$

$dfrac{0.017}{3.9}=dfrac{(3.9)left(dfrac{1}{2} right)^{dfrac{x}{5730}}}{3.9}$

$0.0044=left(dfrac{1}{2} right)^{dfrac{x}{5730}}$

$log0.0044=logleft( dfrac{1}{2}right)^{dfrac{x}{5730}}$

$log0.0044=dfrac{x}{5730}log dfrac{1}{2}$

$-2.3606=left(dfrac{x}{5730} right)(-0.3010)$

$-2.3606=-0.000 05x$

$dfrac{-2.3606}{-0.00005}=dfrac{-0.00005x}{-0.000 05}$

$x=44 933$

The closest answer is $45000$ years, so the correct answer is a).

In each of the next $5$ years, the cost of goods and services will increase by $3.1$ percent. In other words, in each of the next $5$ years, the cost of goods and services will be $103.1$ percent of what it was the previous year.Since $103.1$ percent written as a decimal is $1.031$, the cost of goods and services now should be multiplied by $(1.031)^t$ to find the cost of goods and services after $t$ years. Since the cost of good and services now is $P$, $textbf{the correct answer is c).}$

If the population of a city is currently $150 000$ and is increasing at $2.3$ percent per year, the population of the city in $6$ years can be calculated as follows:

$P=(150 000)(1.023)^6$

$P=(150 000)(1.1462)$

$P=171 927$

Since the population in $6$ years will be $171 927$, and since the population is increasing at $2.3$ percent per year, the number of people by which the population will increase in the $7$th year from now will be $(171 927)(0.023)=3954$. The closest answer is $4000$, so $textbf{the correct answer is c)}$.

It’s apparent from the graph that as $x$ moves away from $0$ in the negative direction, $y$ becomes smaller and smaller, while as $x$moves away from $0$ in the positive direction, $y$ becomes larger and larger. For this reason,(a) cannot be the correct answer, since as $x$ moves away from $0$ in the negative direction, $x^2$ becomes larger and larger. Also, (b) cannot be the correct answer, since the domain of $log x$ is $left{xinBbb{R}|x>0 right}$, and (d) cannot be the correct answer, since as $x$ moves away from $0$ in the positive direction, $0.5^x$ becomes smaller and smaller. Therefore, $textbf{the correct answer is c)}$.

The domain of $f-g$ is the intersection of the domain of $f$ and the domian of $g$. Since the domain of $f$ is $left{xinBbb{R}|x>0 right}$, and the domain of $g$ is $left{xinBbb{R}|xne3 right}$,the domain of $f-g$ is $left{ xinBbb{R}|x>0, xne 3right}$.Therefore, $textbf{the correct answer is b)}$.

The sum or difference of an odd function and an even function is neither even nor odd,unless one of the functions is identically zero, so neither (b) nor (c) can be the correct answer. The difference of two even functions is even, so (d) cannot be the correct answer. Since the sum of two odd functions is always an odd function,$textbf{the correct answer is a)}$.

If $f(x)=g(x)=sec x$, then $f(x)times g(x)=sec^2 x$.Since the range of both $f(x)=sec x$ and $g(x)=sec x$ is $left{yinBbb{R}|-1geq ygeq1 right}$, the range of $f(x)times g(x)=sec^2 x$ must be $left{yinBbb{R}|ygeq 1 right}$. This is because a negative number squared is always positive, and $(-1)^2=1$. Therefore, $textbf{the correct answer is a)}$.

If $f(x)=ax^2+3$ and $g(x)=bx-1$, then $(ftimes g)(x)$ can be calculated as follows:

$(ftimes g)(x)=(ax^2+3)(bx-1)$

$(ftimes g)(x)=abx^3-ax^2+3bx-3$

Since $(ftimes g)(x)$ passes through the point $(-1,-3)$, the function can be rewritten as follows:

$-3=ab(-1)^3-a(-1)^2+3b(-1)-3$

$-3=-ab-a-3b-3$

$-3+3=-ab-a-3b-3+3$

$0=-ab-a-3b$

Also, since $(ftimes g)(x)$ passes through the point $(1,9)$, the function can be rewritten as follows:

$9=ab(1)^3-a(1)^2+3b(1)-3$

$9=ab-a+3b-3$

$9+3=ab-a+3b-3+3$

$12=ab-a+3b$

If the equations $0=-ab-a-3b$ and $12=ab-a+3b$ are added together, the resulting equation is $12=-2a$, or $a=-6$.

If $-6$ is substituted for $a$ into the equation $0=-ab-a-3b$, the equation can be rewritten as follows:

$0=-(-6)b-(-6)-3b$

$0=6b+6-3b$

$0=3b+6$

$0-6=3b+6-6$

$3b=-6$

$b=-2$

Therefore, $textbf{The correct answer is d)}$.

Since $f(x)=log x$ and $g(x)=|x-2|$, $(fdiv g)(x)=dfrac{log x}{|x-2|}$. Since the denominator can never equal $0$, $x$ can never equal $2$. Also, since it’s impossible to find the log of a number less than or equal to $0$, $x$ must be greater than $0$. Therefore, the domain of $(fdiv g)(x)$ is $left{ xinBbb{R}|x>0, xne 2right}$, and $textbf{the correct answer is d).}$

The domain of $f(x)=sqrt{3-x}$ is $left{xinBbb{R}|xleq3 right}$. For this reason, the rangeof $g(x)=3x^2$ that is permissible is $left{yinBbb{R}|yleq 3 right}$, and the domain of $f circ g$ can be calculated as follows:

$3x^2leq 3$

$dfrac{3x^2}{3}leqdfrac{3}{3}$

$x^2leq 1$

$-1leq x leq 1$

Therefore, the domain of $f circ g$ is $left{xinBbb{R}|-1leq xleq 1 right}$, and $textbf{the correct answer is c)}$.

It’s clear from the graph that two points on the line are $(0,3)$ and $(4, -5)$. Since it is already known from the point $(0,3)$ that the $y$-intercept of the line is $3$, all that is needed to determine the equation of the line is its slope. The slope of the line can be calculated as follows:

$m=dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}$

$m=dfrac{-5-3}{4-0}$

$m=dfrac{-8}{4}$

$m=-2$

Since the $y$-intercept of the line is $3$ and the slope of the line is $-2$, the equation of the line is $y=-2x+3$.
Because $(h circ f)(x)=3-2x=-2x+3$, $textbf{the correct answer is d)}$.

To solve the equation $x^3=sqrt[3]{tan x}$, first subtract $sqrt[3]{tan x}$ from both sides of the equation to produce the equation $x^3-sqrt[3]{tan x}=0$. Then graph the function $f(x)=x^3-sqrt[3]{tan x}$ and detrmine the $x$-coordinates of the points where graph crosses the $x$-axis these are the solutions to the equation. The graph of $f(x)=x^3-sqrt[3]{tan x}$ is as follows:

The graph crosses the $x$-axis at about $x=-1.55$,$-1.07$, $0$,$1.07$, and $1.55$. Therefore, $textbf{the correct answer is d)}$.

The functions $f(x)=4-x^2$ and $g(x)=-3x$ graphed on the same coordinategrid are as follows:

It’s apparent from the grah that $f(x)< g(x)$ when $x4$. Therefore, $textbf{the correct answer is b)}$.

Since the horizonatal distance that a football can be thrown can be modelled

by the function $d=dfrac{v^2}{9.8}sin 2 theta+1.8$, the angle at which the

football was thrown can be calculated as follows:

$d=dfrac{v^2}{9.8}sin 2theta +1.8$

$35=dfrac{20^2}{9.8}sin 2theta+1.8$

$35=dfrac{400}{9.8}sin 2theta+1.8$

$35-1.8=dfrac{400}{9.8}sin 2theta+1.8-1.8$

$33.2=dfrac{400}{9.8}sin2theta$

$33.2timesdfrac{9.8}{400}=dfrac{400}{9.8}sin 2thetatimesdfrac{9.8}{400}$

$sin2theta=0.8134$

$sin^{-1}(sin2theta)=sin^{-1}(0.8134)$

$2theta=54.4295^{circ}$ or $125.5705^{circ}$

$dfrac{2theta}{2}=dfrac{54.4295^{circ}}{2}$ or $dfrac{125.5705^{circ}}{2}$

$theta=27^{circ}$ or $63^{circ}$

Therefore, $textbf{the football could have been thrown at either $27^{circ}$ or $63^{circ}$ relative to horizontal.}$

$27^{circ}$ or $63^{circ}$

#### (a)

Answers may vary. For example, since population growth is usually exponential, suitable models for the population of Niagara an Waterloo could be exponential functions in the form $P(x)=ab^x$. If the year $1996$ is considered $t=0$, the model for Niagara can be developed as follows:

$P(x)=ab^x$

$414.8=ab^0$

$414.8=a(1)$

$a=414.8$

Since $a=414.8$, the model can now be developed as follows:

$P(x)=(414.8)(b^x)$

$476.8=(414.8)(b^{32})$

$dfrac{476.8}{414.8}=dfrac{(414.8)(b^{32})}{414.8}$

$b^{32}=1.1495$

$b=1.0044$

Since $b=1.0044$, the model for Niagara is $P(x)= (414.8)(1.0044^x)$.

The model for Waterloo can be developed as follows:

$P(x)=ab^x$

$418.3=ab^0$

$418.3=a(1)$

$a=418.3$

Since $a=418.3$, the model can now be developed as follows:

$P(x)=(418.3)(b^x)$

$606.1=(418.3)(b^{32})$

$dfrac{606.1}{418.3}=dfrac{(418.3)(b^{32})}{418.3}$

$b^{32}=1.4490$

$b=1.0117$

Since $b=1.0117$, the model for Waterloo is $P(x)=(418.3)(1.0117^x)$.

#### (b)

Answers may vary. For example, to estimate the doubling time for Niagara , the model $P(x)=(414.8)(1.0044^x)$ could be used as follows:

$P(x)=(414.8)(1.0044^x)$

$829.6=(414.8)(1.0044^x)$

$dfrac{829.6}{414.8}=dfrac{(414.8)(1.0044^x)}{414.8}$

$1.0044^x=2$

$log 1.0044^x=log 2$

$(x)(log 1.0044)=log 2$

$dfrac{(x)(log 1.0044)}{log 1.0044}=dfrac{log 2}{log 1.0044}$

$x=dfrac{0.3010}{0.0019}$

$x=159$ years

To estimate the doubling time for Waterloo, the model $P(x)=(418.3)(1.0117^x)$ can be used as follows:

$P(x)=(418.3)(1.0117^x)$

$836.6=(418.3)(1.0117^x)$

$dfrac{836.6}{418.3}=dfrac{(418.3)(1.0117^x)}{418.3}$

$1.0117^x=2$

$log 1.0117^x=log 2$

$(x)(log 1.0117)=log 2$

$dfrac{(x)(log 1.0117)}{log 1.0117}=dfrac{log 2}{log 1.0117}$

$x=dfrac{0.3010}{0.0050}$

$x=60$ years

#### (c)

Answers may vary.For example, to calculate the rate at which Niagara’s population will be growing in $2025$, first it’s necessary to find the projected population in $2024$, and then it’s necessary to find the projected population in $2024$ can be found as follows:

$P(x)=(418.8)(1.0044^{28})$

$P(x)=(414.8)(1.1308)$

$P(x)=469.1$

The projected population in $2025$ can be found as follows:

$P(x)=(414.8)(1.0044^{29})$

$P(x)=(414.8)(1.1358)$

$P(x)=471.1$

Therefore, the rate at which Niagara’s population will be growing in $2025$ is $471.1-469.1=2$ thousand people per year. To calculate the rate at which Waterloo’s population will be growing in $2025$,first it’s necessary to find the projected population in $2025$. The projected population in $2024$ can be found as follows:

$P(x)=(418.3)(1.0117^{28})$

$P(x)=(418.3)(1.3850)$

$P(x)=579.3$

The projected population in $2025$ can be found as follows:

$P(x)=(418.3)(1.0117^{29})$

$P(x)=(418.3)(1.4012)$

$P(x)=586.1$

Therefore, the rate at which Waterloo’s population will be growing in $2025$ is $586.1-579.3=6.8$ thousand people per year. Since Niagar’s population will be growing at $2$ thousand people per year and Waterloo’s population will be growing at $6.8$ thousand people per year, Waterloo’s population will be growing faster.

Since the mass of the rocket just before launch is $30 000$ kg, and since its mass is decreasing at $100$ kg/s, $m(t)=30 000-100t$. Since $T-10m=ma$, a can be isolated as follows:

$T-10m=ma$

$dfrac{T-10m}{m}=dfrac{ma}{m}$

$a=dfrac{T-10m}{m}$

$a=dfrac{T}{m}-10$

Since $m(t)=30 000-100t$, $a(t)$ can be determined as follows:

$a=dfrac{T}{m}-10$

$a(t)=dfrac{T}{30 000-100t}-10$

Since $m=30 000 (2.72)^{-v-gt}$, $v$ can be isolated as follows:

$m=30 000(2.72)^{-v-gt}$

$dfrac{m}{30000}=dfrac{30 000(2.72)^{-v-gt}}{30 000}$

$dfrac{m}{30 000}=(2.72)^{-v-gt}$

$log dfrac{m}{30 000}=log ((2.72)^{-v-gt})$

$logdfrac{m}{30 000}=(-v-gt)(log 2.72)$

$dfrac{logdfrac{m}{30000}}{log 2.72}=dfrac{(-v-gt)(log 2.72)}{log 2.72}$

$-v-gt=dfrac{logdfrac{m}{30 000}}{log 2.72}$

$-v-gt+gt=dfrac{logdfrac{m}{30 000}}{log 2.72}+gt$

$-v=dfrac{logdfrac{m}{30 000}}{log 2.72}+gt$

$-v times -1=left(dfrac{log dfrac{m}{30 000}}{log 2.72}+gt right)times -1$

$v=-dfrac{logdfrac{m}{30 000}}{log 2.72}-gt$

Since $m(t)=30 000-100t$, $v(t)$ can be determined as follows:

$v=-dfrac{logdfrac{m}{30 000}}{log 2.72}-gt$

$v(t)=-dfrac{logdfrac{30 000-100t}{30 000}}{log 2.72}-gt$

$v(t)=-dfrac{logleft( 1-dfrac{t}{300}right)}{log 2.72}-gt$

$v(t)=-dfrac{logleft(1-dfrac{t}{300} right)}{log 2.72}-gt$

In order for the rocket to get off the ground, $a(0)$ must be greater than $0$. Therefore, the constraints on the value of $T$ can be determined as follows:

$a(t)=dfrac{T}{30 000-100t}-10$

$0<dfrac{T}{30 000-100(0)}-10$

$0<dfrac{T}{30 000}-10$

$0+10<dfrac{T}{30000}-10+10$

$10<dfrac{T}{30 000}$

$10times 30 000 300 000$ N