(a) We would like to solve the linear equation $color{#4257b2}5x-7=-3x+17$.

First, we note that it is a linear equation in one variable $color{#4257b2}x$, so we need to make the variable $color{#4257b2}x$ in one side alone and that can be made by adding $color{#4257b2}3x+7$ to each side.

$$
5x-7=-3x+17
$$

$$
5x-7+3x+7=-3x+17+3x+7
$$

$$
5xcancel{-7}+3x+cancel{7}=cancel{-3x}+17+cancel{3x}+7
$$

$$
5x+3x=17+7
$$

$$
8x=24
$$

Now we made the variable $color{#4257b2}x$ in the left side alone, so the next step is to divide the two sides by $color{#4257b2}8$ to find the value of $color{#4257b2}x$.

$$
8x=24
$$

$$
dfrac{8x}{8}=dfrac{24}{8}
$$

$$
boxed{ x=3 }
$$

(b) We would like to solve the linear equation $color{#4257b2}12x-9-6x=5+3x+1$. First, we note that it is a linear equation in one variable $color{#4257b2}x$, so we need to make the variable $color{#4257b2}x$ in one side alone and that can be made by adding $color{#4257b2}9-3x$ to each side.

$$
12x-9-6x=5+3x+1
$$

$$
12x-9-6x+9-3x=5+3x+1+9-3x
$$

$$
12xcancel{-9}-6x+cancel{9}-3x=5+cancel{3x}+1+9cancel{-3x}
$$

$$
12x-6x-3x=5+1+9
$$

$$
3x=15
$$

Now we made the variable $color{#4257b2}x$ in the left side alone, so the next step is to divide the two sides by $color{#4257b2}3$ to find the value of $color{#4257b2}x$.

$$
3x=15
$$

$$
dfrac{3x}{3}=dfrac{15}{3}
$$

$$
boxed{ x=5 }
$$

(c) We would like to solve the linear equation $color{#4257b2}2left(3x-5right)=-4left(3x-2right)$. First, we note that it is a linear equation in one variable $color{#4257b2}x$, so we need to make the variable $color{#4257b2}x$ in one side alone and that can be made by distributing $color{#4257b2}2$ and $color{#4257b2}-4$ to the brackets $color{#4257b2}left(3x-5right)$ and $color{#4257b2}left(3x-2right)$ as the first step.

$$
2left(3x-5right)=-4left(3x-2right)
$$

$$
6x-10=-12x+8
$$

Now we can add $color{#4257b2}12x+10$ to each side to make $color{#4257b2}x$ in the left side alone.

$$
6x-10+12x+10=-12x+8+12x+10
$$

$$
6xcancel{-10}+12x+cancel{10}=cancel{-12x}+8+cancel{12x}+10
$$

$$
6x+12x=8+10
$$

$$
18x=18
$$

Now we made the variable $color{#4257b2}x$ in the left side alone, so the next step is to divide the two sides by $color{#4257b2}18$ to find the value of $color{#4257b2}x$.

$$
18x=18
$$

$$
dfrac{18x}{18}=dfrac{18}{18}
$$

$$
boxed{ x=1 }
$$

(d) We would like to solve the linear equation $color{#4257b2}dfrac{2x+5}{3}=7-dfrac{x}{4}$. First, we note that it is a linear equation in one variable $color{#4257b2}x$, so we need to make the variable $color{#4257b2}x$ in one side alone and that can be made by multiplying the two sides by $color{#4257b2}12$ as the first step to remove the denominators of the two fractions.

$$
dfrac{2x+5}{3}=7-dfrac{x}{4}
$$

$$
12cdot left(dfrac{2x+5}{3}right)=12cdot left(7-dfrac{x}{4}right)
$$

$$
4left(2x+5right)=84-3x
$$

$$
8x+20=84-3x
$$

Now we can add $color{#4257b2}3x-20$ to each side to make $color{#4257b2}x$ in the left side alone.

$$
8x+20+3x-20=84-3x+3x-20
$$

$$
8x+cancel{20}+3xcancel{-20}=84cancel{-3x}+cancel{3x}-20
$$

$$
11x=64
$$

Now we made the variable $color{#4257b2}x$ in the left side alone, so the next step is to divide the two sides by $color{#4257b2}11$ to find the value of $color{#4257b2}x$.

$$
dfrac{11x}{11}=dfrac{64}{11}
$$

$$
boxed{ x=dfrac{64}{11} }
$$

$$
text{color{Brown}$(a) x=3$ $(b) x=5$ $(c) x=1$ $(d) x=dfrac{64}{11}$}
$$

(a) We would like to factor the expression $color{#4257b2}x^{3}+x^{2}-30x=0$.

First, we note that the all terms contain $color{#4257b2}x$, so we can take $color{#4257b2}x$ as a common factor.

$$
x^{3}+x^{2}-30x=0
$$

$$
xleft(x^{2}+x-30right)=0
$$

Now we have a quadratic equation which is multiplied by $color{#4257b2}x$, so we can factor this quadratic equation where it will give us two brackets multiplied by each other.

$$
xleft(x^{2}+x-30right)=0
$$

$$
xleft(x+6right)left(x-5right)=0
$$

Note that we factored the quadratic equation to $color{#4257b2}left(x+6right)left(x-5right)$ because the result of multiplying $color{#4257b2}6$ by $color{#4257b2}-5$ is $color{#4257b2}-30$ such as in the equation and the difference between them is $color{#4257b2}+1$ such as the middle term in the equation.

So the expression $color{#4257b2}x^{3}+x^{2}-30x=0$ can be factored to $boxed{ xleft(x+6right)left(x-5right)=0 }$

(b) We would like to factor the expression $color{#4257b2}x^{3}-64=0$. First, we note that it is a cubic equation on the form $color{#4257b2}x^{3}-a^{3}$, so we can factor it where $color{#4257b2}x^{3}-a^{3}=left(x-aright)left(x^{2}+a x+a^{2}right)$

$$
x^{3}-64=0
$$

$$
left(x-4right)left(x^{2}+4 x+4^{2}right)
$$

$$
left(x-4right)left(x^{2}+4 x+16right)
$$

Note that $color{#4257b2}sqrt[3]{64}=4$, so we put $color{#4257b2}4$ instead of $color{#4257b2}a$ in the form of factoring a cubic equation.

So the expression $color{#4257b2}x^{3}-64=0$ can be factored to $boxed{ left(x-4right)left(x^{2}+4 x+16right)=0 }$

(c) We would like to factor the expression $color{#4257b2}24x^{4}+81x=0$. First, we note that the all terms contain $color{#4257b2}3x$, so we can take $color{#4257b2}3x$ as a common factor.

$$
24x^{4}+81x=0
$$

$$
3xleft(8x^{3}+27right)=0
$$

Now we have a cubic equation on the form $color{#4257b2} a^{3}x^{3}+b^{3}$, so we can factor it where $color{#4257b2} a^{3}x^{3}+b^{3}=left( ax+bright)left( a^{2}x^{2}-a b x+b^{2}right)$

$$
3xleft(8x^{3}+27right)=0
$$

$$
3xleft(2x+3right)left(2^{2}cdot x^{2}-2cdot 3 x+3^{2}right)
$$

$$
3xleft(2x+3right)left(4x^{2}-6 x+9right)
$$

Note that $color{#4257b2}sqrt[3]{8}=2$ and $color{#4257b2}sqrt[3]{27}=3$, so we put $color{#4257b2}2$ and $color{#4257b2}3$ instead of $color{#4257b2}a$ and $color{#4257b2}3$ in the form of factoring a cubic equation.

So the expression $color{#4257b2}24x^{4}+81x=0$ can be factored to $boxed{ 3xleft(2x+3right)left(4x^{2}-6 x+9right)=0 }$

(d) We would like to factor the expression $color{#4257b2}2x^{3}+7x^{2}-18x-63=0$. First, we note that our expression consists of four terms, so we can make two terms in bracket and add them to the other two terms.

$$
2x^{3}+7x^{2}-18x-63=0
$$

$$
left(2x^{3}-18xright)+left(7x^{2}-63right)=0
$$

Now we have two brackets each of them contains a quadratic equation, so we can take $color{#4257b2}2x$ as a common factor from the first bracket and take $color{#4257b2}7$ as a common factor from the second bracket.

$$
left(2x^{3}-18xright)+left(7x^{2}-63right)=0
$$

$$
2xleft(x^{2}-9right)+7left(x^{2}-9right)=0
$$

Now we note that the two terms each of them contain the bracket $color{#4257b2}x^{2}-9$, so we can take it as a common factor.

$$
2xleft(x^{2}-9right)+7left(x^{2}-9right)=0
$$

$$
left(x^{2}-9right)left(2x+7right)=0
$$

Now we note that the first bracket is a quadratic equation on the form $color{#4257b2}x^{2}-a^{2}$ which can be factored to $color{#4257b2}left(x-aright)left(x+aright)$, so we can factor $color{#4257b2}x^{2}-9$ to $color{#4257b2}left(x-3right)left(x+3right)$

$$
left(x^{2}-9right)left(2x+7right)=0
$$

$$
left(x-3right)left(x+3right)left(2x+7right)=0
$$

So the expression $color{#4257b2}2x^{3}+7x^{2}-18x-63=0$ can be factored to $boxed{ left(x-3right)left(x+3right)left(2x+7right)=0 }$

$$
text{color{Brown}$(a) xleft(x+6right)left(x-5right)=0$
\
\
$(b) left(x-4right)left(x^{2}+4 x+16right)=0$
\
\
$(c) 3xleft(2x+3right)left(4x^{2}-6 x+9right)=0$
\
\
$(d) left(x-3right)left(x+3right)left(2x+7right)=0$}
$$

Sketch a graph for the following function

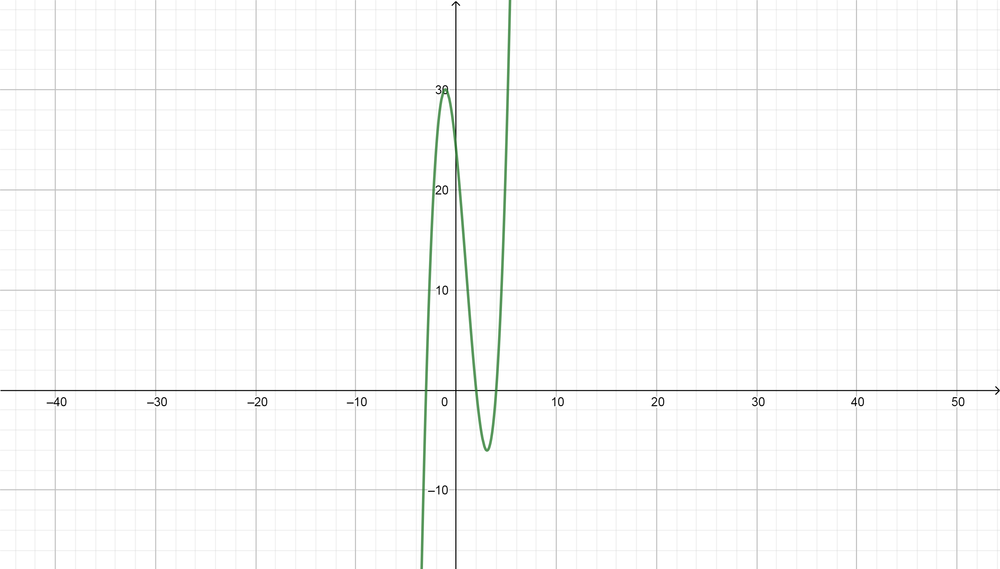
$$
color{#4257b2}text{(a)} y=(x-2)(x+3)(x-4)
$$

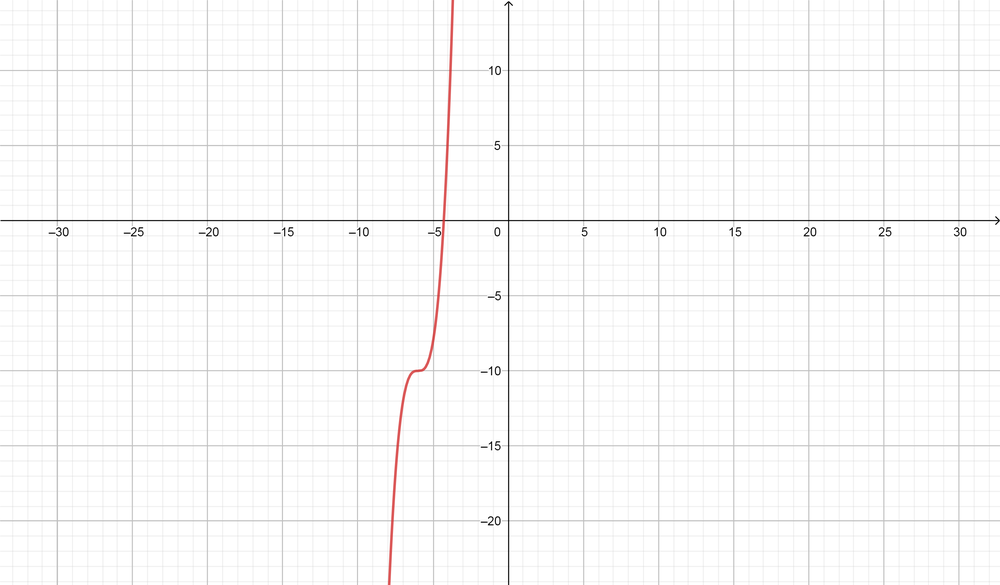
$$
color{#4257b2}text{(b)} y=2(x+6)^3-10
$$

$$
text{color{Brown} See graphs}
$$

We would like to determine the roots of the equation $color{#4257b2}x^{2}-7x+10=0$ since we have the graph of the equation $color{#4257b2}y=x^{2}-7x+10$, so we need to find the points that the function $color{#4257b2}y=x^{2}-7x+10$ intersects with the x-axis and then find the values of $color{#4257b2}x$ at these points.

We note that the graph of the function $color{#4257b2}y=x^{2}-7x+10$ intersects with the x-axis at the points $color{#4257b2}A$ and $color{#4257b2}B$ where the values of $color{#4257b2}x$ at these points are $color{#4257b2}x=2$ and $color{#4257b2}x=5$.

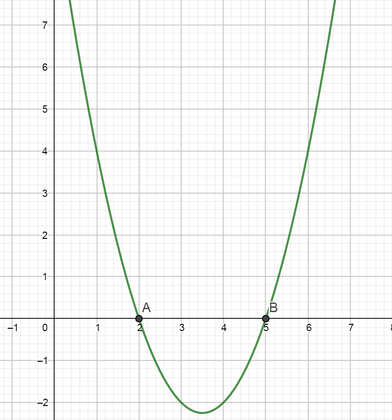
So the roots of the equation $color{#4257b2}x^{2}-7x+10=0$ are $boxed{ x=2 } text{or} boxed{ x=5 }$

Large{$text{color{Brown}$x=2 {color{Black}text{or}} x=5$}$

(a) We would like to determine the roots of the quadratic equation $color{#4257b2}2x^{2}=18$. First, we can subtract $color{#4257b2}18$ from each side to make the right side zero.

$$
2x^{2}=18
$$

$$
2x^{2}-18=18-18
$$

$$
2x^{2}-18=0
$$

Now we can take $color{#4257b2}2$ as a common factor.

$$
2left(x^{2}-9right)=0
$$

Now we have a quadratic equation on the form $color{#4257b2}a^{2}-b^{2}$, so we can factor this quadratic equation where $color{#4257b2}a^{2}-b^{2}=left(a+bright)left(a-bright)$.

$$
2left(x^{2}-9right)=0
$$

$$
2left(x+3right)left(x-3right)=0
$$

$$
left(x+3right)left(x-3right)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$

$$
x+3=0 text{or} x-3=0
$$

$$
x=-3 text{or} x=3
$$

So the roots of the equation $color{#4257b2}2x^{2}=18$ are $boxed{ x=-3 } text{or} boxed{ x=3 }$

(b) Since we would like to determine the roots of the quadratic equation $color{#4257b2}x^{2}+8x-20=0$, so we can factor to find the values of $color{#4257b2}x$.

$$
x^{2}+8x-20=0
$$

$$
left(x+10right)left(x-2right)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$

$$
x+10=0 text{or} x-2=0
$$

$$
x=-10 text{or} x=2
$$

So the roots of the equation $color{#4257b2}x^{2}+8x-20=0$ are $boxed{ x=-10 } text{or} boxed{ x=2 }$

(c) We would like to determine the roots of the quadratic equation $color{#4257b2}6x^{2}=11x+10$. First, we can subtract $color{#4257b2}11x+10$ from each side to make the right side zero.

$$
6x^{2}=11x+10
$$

$$
6x^{2}-11x-10=11x+10-11x-10
$$

$$
6x^{2}-11x-10=0
$$

Now we can have a quadratic equation, so we can factor to find the values of $color{#4257b2}x$.

$$
left(3x+2right)left(2x-5right)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
3x+2=0 text{or} 2x-5=0
$$

$$
3x=-2 text{or} 2x=5
$$

$$
x=-dfrac{2}{3} text{or} x=dfrac{5}{2}
$$

So the roots of the equation $color{#4257b2}6x^{2}=11x+10$ are $boxed{ x=-dfrac{2}{3} } text{or} boxed{ x=dfrac{5}{2} }$

(d) We would like to determine the roots of the quadratic equation
$color{#4257b2}xleft(x+3right)=3-5x-x^{2}$. First, we can distribute $color{#4257b2}x$ which is multiplied by the bracket $color{#4257b2}left(x+3right)$.

$$
xleft(x+3right)=3-5x-x^{2}
$$

$$
x^{2}+3x=3-5x-x^{2}
$$

Now we can add $color{#4257b2}x^{2}+5x-3$ to each side to make the right side zero.

$$
x^{2}+3x+x^{2}+5x-3=3-5x-x^{2}+x^{2}+5x-3
$$

$$
2x^{2}+8x-3=0
$$

Now we can have a quadratic equation on the standard form $color{#4257b2}a x^{2}+b x +c=0$, so we can use the quadratic formula $color{#4257b2}x=dfrac{-bpm sqrt{b^{2}-4ac}}{2a}$ to find the values of $color{#4257b2}x$.

$$
x=dfrac{-bpm sqrt{b^{2}-4ac}}{2a}
$$

$$
x=dfrac{-8pm sqrt{(8)^{2}-4cdot 2cdot (-3)}}{2cdot 2}
$$

Note that $color{#4257b2}a=2, b=8$ and $color{#4257b2}x=-3$

$$
x=dfrac{-8pm sqrt{64+24}}{4}
$$

$$
x=dfrac{-8pm sqrt{88}}{4}
$$

$$
x=dfrac{-8pm 2sqrt{22}}{4}
$$

$$
x=dfrac{-4pm sqrt{22}}{2}
$$

So the roots of the equation $color{#4257b2}xleft(x+3right)=3-5x-x^{2}$ are $boxed{ x=dfrac{-4+ sqrt{22}}{2} } text{or} boxed{ x=dfrac{-4- sqrt{22}}{2} }$

$$
text{color{Brown}$(a) x=-3 {color{Black}text{or}} x=3$
\
\
$(b) x=-10 {color{Black}text{or}} x=2$
\
\
$(c) x=-dfrac{2}{3} {color{Black}text{or}} x=dfrac{5}{2}$
\
\
$(d) x=dfrac{-4+sqrt{22}}{2} {color{Black}text{or}} x=dfrac{-4-sqrt{22}}{2}$}
$$

$$
{color{#4257b2}text{(a)} In which time interval she walking the fastest.}
$$

She walked fastest in the interval of time at $tin (3, 7)$

$$
{color{#4257b2}text{(b)} Calculate the speed on the internal of time at $tin (0, 3)$ and $tin (3, 7)$.}
$$

For time at $tin (0, 3)$

Note that, speed $=dfrac{text{distance}}{text{time}}$

Speed$=dfrac{2-0}{3-0}$ Speed$=dfrac{2}{3}$ m/s

For time at $tin (3, 7)$

Note that, speed $=dfrac{text{distance}}{text{time}}$

Speed$=dfrac{5-2}{7-3}$ Speed$=dfrac{3}{4}$ m/s

$$
{color{#4257b2}text{(c)} Is moving away or toward to the motion sensor.}
$$

She is moving toward a motion sensor because she move with speed in the interval of time at $tin (3, 7)$ with speed of $=dfrac{3}{4}$ m/s

$$
text{color{Brown} (a) She walked fastest in the interval of time at $tin (3, 7)$
\ \
(b) Speed$=dfrac{2}{3}$ m/s Speed$=dfrac{3}{4}$ m/s
\ \
(c) She is moving toward a motion sensor because she move with speed in the interval of time at $tin (3, 7)$ with speed of $ =dfrac{3}{4}$ m/s}
$$

Complete the table in the textbook.

(a) The quadratic formula can only be used when solving a quadratic equation. $text{color{#4257b2}Agree}$

(b) Cubic equation always have three real root. $text{color{#4257b2}Disagree}$

(c) The graph of cubic function always passes through all four quadrant. $text{color{#4257b2}Disagree}$

(d) The graph of all polynomial function must pass through at least two quadrant. $text{color{#4257b2}Agree}$

(e) The expression $x^2>4$ is only true if $x>2$. $text{color{#4257b2}Agree}$

(f) If know the instantaneous rate of change for function at $x=2, x=3$ you can predict what function look like between. $text{color{#4257b2}Agree}$

$$
text{color{Brown}(a) Agree (b) Disagree
\ \
(c) Disagree (d) Agree
\ \
(e) Agree (f) Agree}
$$