#### (a)

$(ftimes g)(x)={(0,2 times -1), (1,5 times -2), (2,7 times 3), (3,12 times 5)}$={(0, -2), (1, -10), (2, 21), (3,60)}

#### (b)

$(ftimes g)(x)={(0,3 times 4), (2,10 times -2)}={(0,12), (2, -20)}$

$(ftimes g)(x)=x(4)=4x$

#### (d)

$(ftimes g)(x)=x(2x)=2x^2$

#### (e)

$(ftimes g)(x)=(x+2)(x^2-2x+1)$

$=x^3-2x^2+x+2x^2-4x+2$

$=x^3-3x+2$

#### (f)

$(ftimes g)(x)=2^x(sqrt{x-2})$

$=2^xsqrt{x-2}$

#### (a)

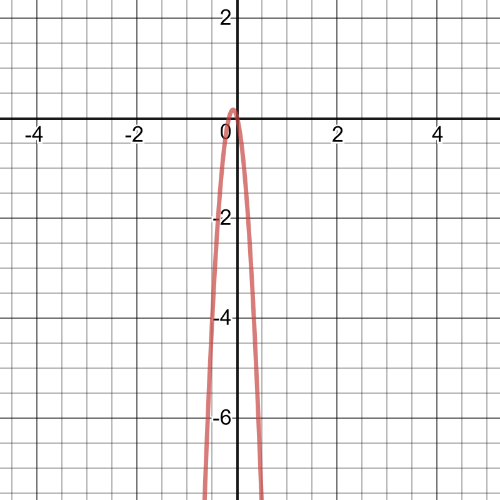
1.task, part (c), red is graph of the function $f(x)$ and blue is of $g(x)$.

1.task, part (d), red is graph of the function $f(x)$ and blue is of $g(x)$.

1.task, part (e), red is graph of the function $f(x)$ and blue is of $g(x)$.

1.task, part (f), red is graph of the function $f(x)$ and blue is of $g(x)$.

#### (b)

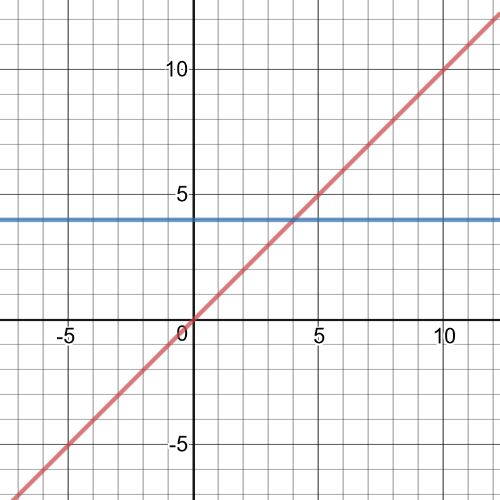
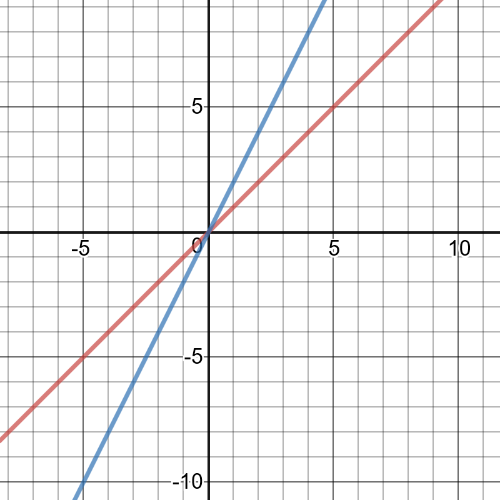
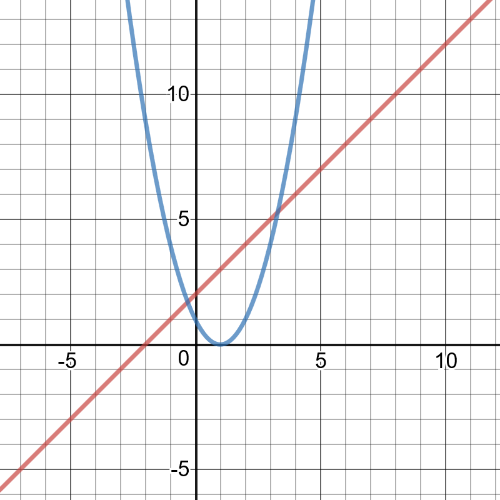
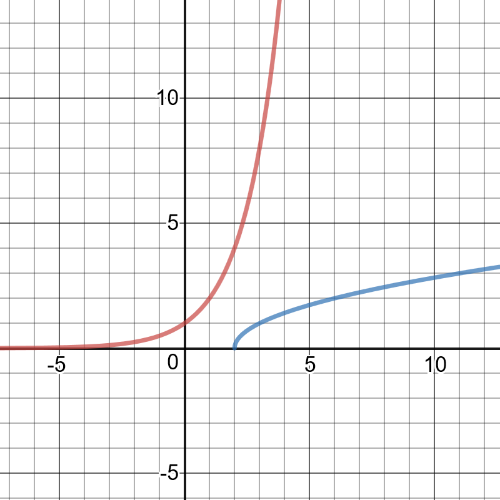
1.task, part (c), $f:left{xinBbb{R} right}$, $g:left{xinBbb{R} right}$

1.task, part (d), $f:left{xinBbb{R} right}$, $g:left{xinBbb{R} right}$

1.task, part (e), $f:left{xinBbb{R} right}$, $g:left{xinBbb{R} right}$

1.task, part (f), $f:left{xinBbb{R} right}$, $g:left{xinBbb{R}|xgeq2 right}$

#### (c)

The graph of $ftimes{g}$ can be found by multipliying corresponding $y-coordinates$.

1.task, part (c), on the following picture there is a graph of $ftimes{g}$:

1.task, part (d), on the following picture there is a graph of $ftimes{g}$:

1.task, part (e), on the following picture there is a graph of $ftimes{g}$:

1.task, part (f), on the following picture there is a graph of $ftimes{g}$:

$(ftimes g )(x)=(sqrt{1+x})(sqrt{1-x})$

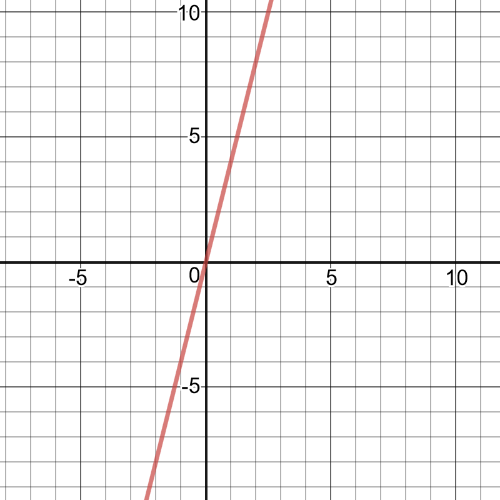
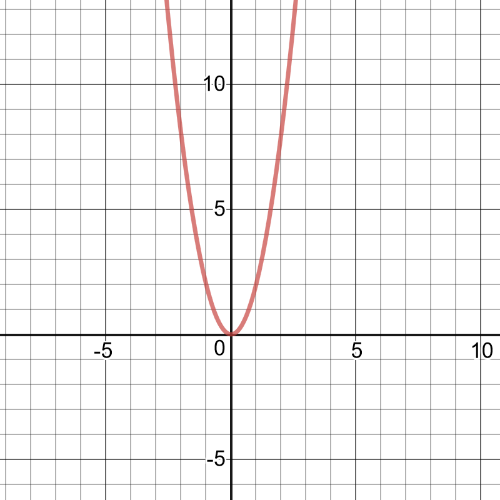
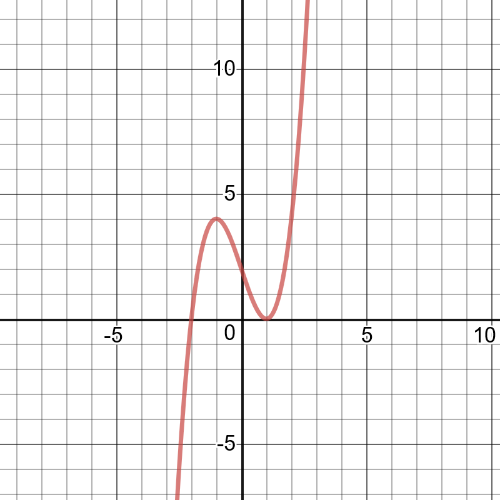
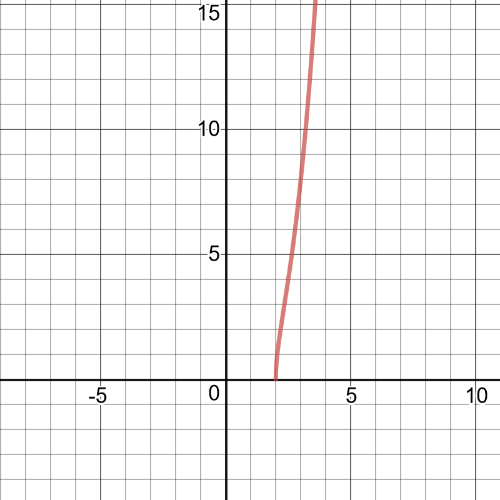
So,$xgeq-1$ and $xleq 1$ since the radicand must be greater than or equal to $0$.

So,the domain is $left{xinBbb{R}|-1leq x leq 1 right}$

#### (a)

$(ftimes g)(x)=(x-7)(x+7)=x^2-49$

#### (b)

$(ftimes g)(x)=(sqrt{x+10})(sqrt{x+10})=x+10$

#### (c)

$(ftimes g)(x)=7x^2(x-9)=7x^3-63x^2$

#### (d)

$(ftimes g)(x)=(-4x-7)(4x+7)=-16x^2-28x-28x-49=16x^2-56x-49$

#### (e)

$(ftimes g)(x)=2sin xleft(dfrac{1}{x-1} right)=dfrac{2sin x}{x-1}$

#### (f)

$(ftimes g)(x)=log (x+4)(2^x)=2^x log (x+4)$

4(a): $D=left{xinBbb{R} right}$; $R=left{y in Bbb{R}|ygeq-49 right}$

4(b): $D=left{xinBbb{R}|xgeq -10 right}$; $R=left{yin Bbb{R}|ygeq0 right}$

4(c): $D=left{ xinBbb{R}right}$; $R=left{yinBbb{R} right}$

4(d): $D=left{ xinBbb{R}right}$; $R=left{yinBbb{R}|yleq0 right}$

4(e): $D=left{ xinBbb{R} | xne -1right}$; $R=left{yin Bbb{R} right}$

4(f): $D=left{xinBbb{R}|x > -4 right}$; $R=left{yinBbb{R}|ygeq 0 right}$

4(a): symmetry: The function is symmetric about the line $x=0$.
increasing/decreasing: The function is increasing from $0$to $infty$. The function is is decreasing from $-infty$ to $0$.
zeros: $x=-7, 7$

maximum/minimum: The minimum is at $x=0$.

period: N/A

4(b): symmetry: The function is not symmetric.
increasing/decreasing: The function is increasing from $-10$ to $infty$.

zeros: $x= -10$

maximum/minimum: The minimum is at $x=-10$.

period: N/A

4(c): symmetry: The function is not symmetic.
increasing/decreasing: The function is increasing from $-infty$to $0$ and from $-infty$ to $0$ and from $6$ to $infty$.

zeros: $x=0,9$

maximum/minimum: The relative minimum is at $x=-6$. The relative maximum is at $x=0$.

period: N/A

4(d): symmetry: The function is symmetric about the line $x=-1.75$.

increasing/decreasing: The function is increasing from $-infty$ to $-1.75$ and is decreasing from $-1.75$ to $infty$.

zero: $x=-1.75$

maximum/minimum: The maximum is at $x=-1.75$.

period: N/A

4(e): symmetry: The function is not symmetric.
increasing/decreasing: The function is increasing from $-infty$ to $0$ and from $6$ to $infty$.

zeros: $x=0,9$

maximum/minimum: The relative minima are at $x=-4.5336$ and $4.4286$.The relative maximum is at $x=-1.1323$.

period: N/A

4(f): symmetry: The function is not symmetric.
increasing/decreasing: The function is increasing from $-4$ to $infty$.

zeros: none

maximum/minimum: none

period: N/A

$f(x)=-4x$

$g(x)=6x+1$

$(ftimes g)(x)= -4x(6x+1)=-24x^2-4x$

#### (a)

$left{xinBbb{R}|xne -2,7, dfrac{pi}{2},or dfrac{3pi}{2} right}$

#### (b)

$left{xinBbb{R}|x>8 right}$

#### (c)

$left{xinBbb{R}|xgeq-81 (and) xne0,pi, or 2pi right}$

#### (d)

$$
left{xinBbb{R}|xleq -1 or x geq 1 (and) xne -3 right}
$$

$(ftimes p)(t)$ represents the total energy consumption in a particular country at time $t$.

$(ftimes p)(t)$

#### (a)

$R(x)=(20 000-750x)(25+x)$ or $R(x)=500 000+1250x-750x^2$, where $x$ is the increase in the admission fee in dollars

#### (b)

Yes, it’s the product of the function $P(x)=20000-750x$, which represents the number of daily visitors, and $F(x)=25+x$, which represents the admission fee.

#### (c)

Use a graphing calculator. The ticket price that will maximize revenue is 25.83$.

$m(t)=((0.9)^t)(650+300t)$

Use a graphing calculator to estimate.

$$
textbf{The amount of contaminated material is at its greatest after about $7.3$s.}
$$

$7.3$s

The statement is false. If $f(x)$ and $g(x)$ are odd functions, then their product will always be an even function. The reason is because when you multiply a function that has an odd degree with another function that has an odd degree, you add the exponents and when you add two odd numbers together, you get an even number.

$h(x)=(mx^2+2x+5)(2x^2-nx-2)$

$-40=(m(1)^2+2(1)+5) times(2(1)^2-n(1)-2)$

$-40=(m+2+5)(2-n-2)$

$-40=(m+7)(-n)$

$dfrac{40}{m+7}=n$ EQUATION 1

$24=(m(-1)^2+2(-1)+5)times (2(-1)^2-n(-1)-2)$

$24=(m-2+5)(2+n-2)$

$24=(m+3)(n)$

$dfrac{24}{m+3}=n$ EQUATION 2

$dfrac{40}{m+7}=dfrac{24}{m+3}$

$40(m+3)=24(m+7)$

$40m+120=24m+168$

$16m=48$

$m=3$

$dfrac{24}{3+3}=n$

$dfrac{24}{6}=n$

$4=n$

$$
textbf{So, the equations are $f(x)=3x^2+2x+5$ and $g(x)=2x^2-4x-2$.}
$$

$f(x)=3x^2+2x+5$ and $g(x)=2x^2-4x-2$

#### (a)

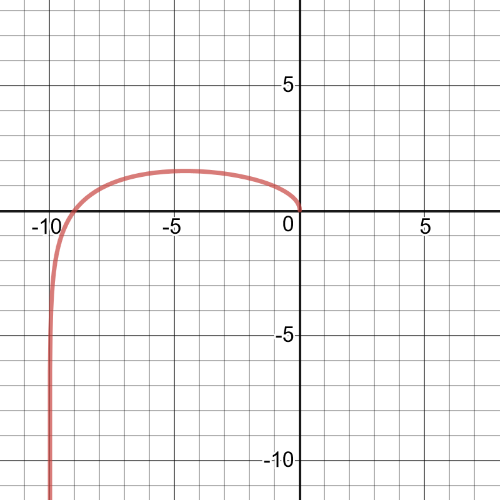
$(ftimes g)(x)=sqrt{-x}log(x+10)$

The domain is $left{xinBbb{R}| -10 < x leq 0 right}$.

#### (b)

One strategy is to create a table of values for $f(x)$ and $g(x)$ and to multiply the corresponding $y$-values together. The resulting values could then be graphed.Another strategy is to graph $f(x)$ and $g(x)$ and to then create a graph for $(ftimes g)(x)$ based on these two graphs. The first strategy is probably better than the second strategy, since the $y$-values for $f(x)$ and $g(x)$ will not be round numbers and will not be easily discernable from the graphs of $f(x)$ and $g(x)$.

#### (c)

#### (a)

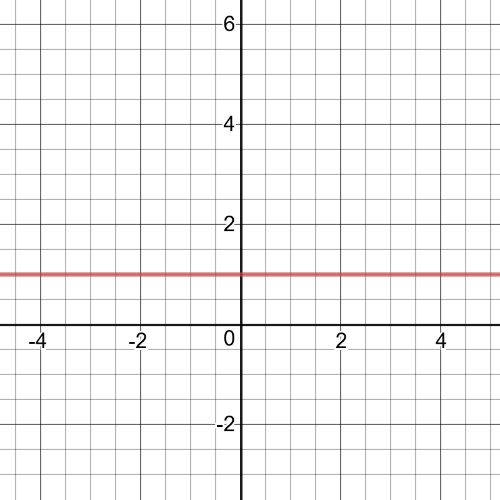
$f(x)times dfrac{1}{f(x)}=(x^2-25)times dfrac{1}{x^2-25}$

#### (b)

The domain of the function is $left{xinBbb{R}|xne -5 (or) 5 right}$.

#### (c)

The range will always be $1$. If $f$ is of odd degree, there will always be at least one value that makes the product undefined and which is excluded from the domain. If $f$ is of even degree, there may be no values that are excluded from domain.

#### (a)

$f(x)=2^x$

$g(x)=x^2+1$

$(ftimes g)(x)=2^x(x^2+1)$

#### (b)

$f(x)=x$

$g(x)=sin(2pi x)$

$(ftimes g)(x)=x sin(2pi x)$

#### (a)

$4x^2-91=(2x+9)(2x-9)$

$f(x)=(2x+9)$

$g(x)=(2x-9)$

#### (b)

$8sin^3 x+27=(2sin x +3)times(4sin^2x-6sin x+9)$

$f(x)=(2sin x+3)$

$g(x)=(4sin^2x-6sin x+9)$

#### (c)

$4x^{dfrac{5}{2}}-3x^{dfrac{3}{2}}+x^{dfrac{1}{2}}=x^{dfrac{1}{2}}(4x^5-3x^3+1)$

$f(x)=x^{dfrac{1}{2}}$

$g(x)=(4x^5-3x^3+1)$

#### (d)

$dfrac{6x-5}{2x+1}=dfrac{1}{2x+1}times 6x-5$

$f(x)=dfrac{1}{2x+1}$

$g(x)=6x-5$