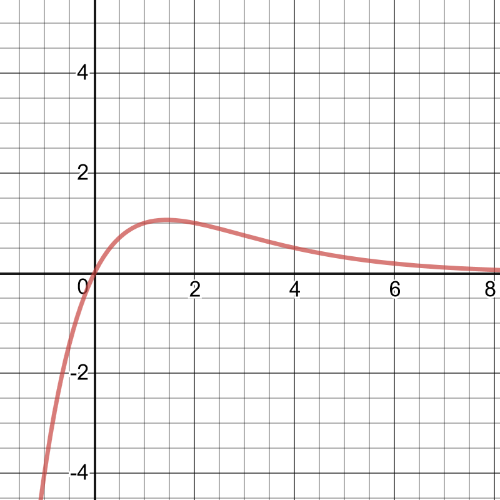
A function with $textbf{a vertical asymptote}$ and $textbf{a horizontal asymptote}$.If the function $y=2^x$ and $y=2x$ are multiplied, the resulting function will have a vertical asymptote and a horizontal asymptote.For example, it could be a function $y=2^x(2x)$.

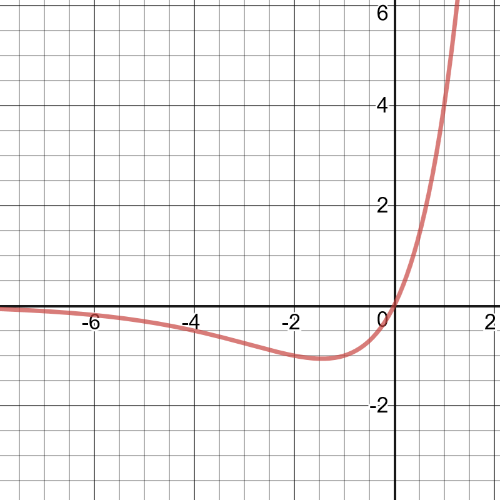
A function that is $textbf{even}$:

$y=2x$ is odd,

$y=cos(2pi{x})$ is odd.

$textbf{The product of the two odd functions will be even.}$For example, it could be a function:

$$
y=(2x)cos(2pi{x})
$$

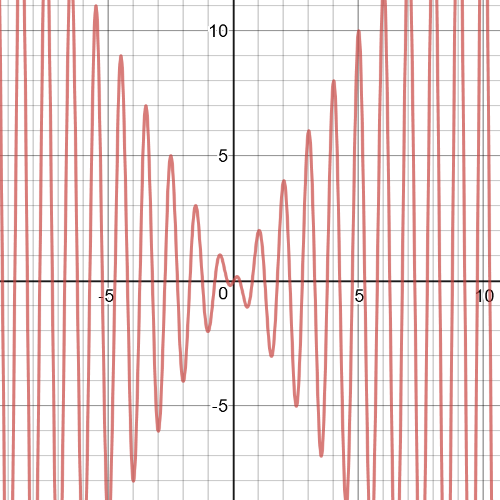
A function that is $textbf{odd}$:

$y=2x$ is odd,

$y=sin(2pi{x})$ is even.

$textbf{The product of the two functions where is one odd and the other one is even is odd.}$For example, it could be a function $y=(2x)sin(2pi{x})$.

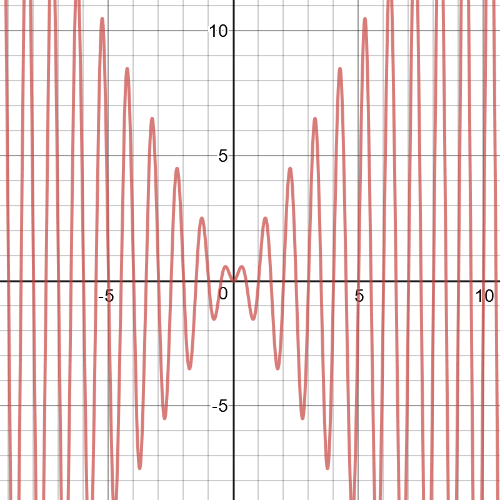
A function that is $textbf{periodic}$:

$y=sin(2pi{x})$ is periodic,

$y=cos(2pi{x})$ is periodic.

$textbf{The product of two periodic function is periodic function.}$So, for example, it could be a function $y=sin(2pi{x})cos(2pi{x})$.

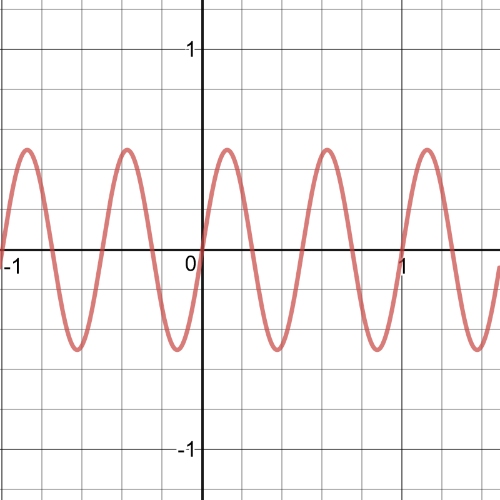
A function that resembles $textbf{a periodic function with decreasing maximum values and increasing minimum values:}$

$y=cos(2pi{x})$ is periodic,

$y=(dfrac{1}{2})^x$ is decreasing.

$textbf{The product of those two functions will be a function that resembles a periodic function with decreasing maximum values and increasing minimum values}$.So, it could be a function $y=(dfrac{1}{2})^xcos(2pi{x})$ where $0leq{x}leq2pi$.

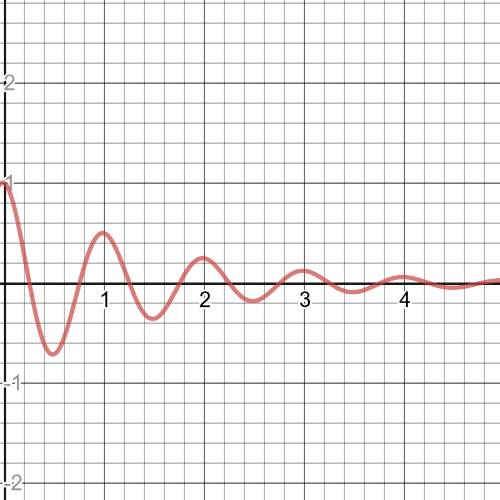
A function that resembles $textbf{a periodic function with increasing maximum values and decreasing minimum values}$:

$y=sin(2pi{x})$ is periodic.

$y=2x$ is increasing.

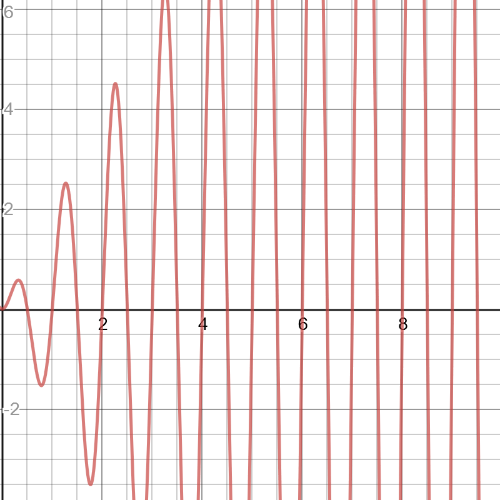
$textbf{The product of those two functions will be a function that resembles a periodic function with increasing maximum values and decreasing minimum values.}$So, it could be a function $y=2xcos(2pi{x})$,

where $0leq{x}leq2pi$.

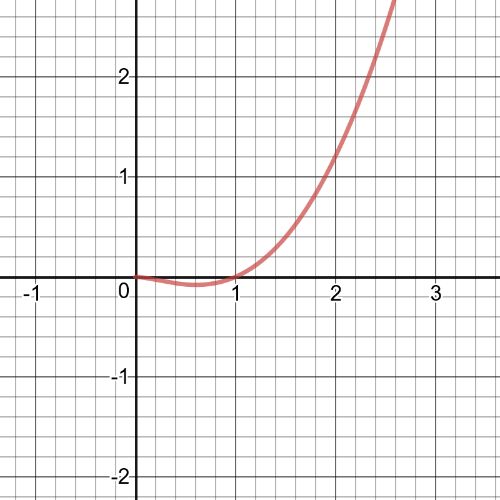
$y=x^2$

$y=log{x}$.

$textbf{The product}$ will be $y=x^2log{x}$, on the following picture there is its $textbf{graph}$.