(a) We would like to solve the equation $color{#4257b2}log_{2} x=2log_{2} 5$. First, we note that the right side is a logarithm which is multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{m} x=log_{m} x^{r}$.

$$
log_{2} x=2log_{2} 5
$$

$$
log_{2} x=log_{2} 5^{2}
$$

$$
log_{2} x=log_{2} 25
$$

Now we note that the two side each of them is a logarithm with the base $color{#4257b2}2$, so the the two expressions must equal each other because we know that if $color{#4257b2}log_{a} M=log_{a} N$, then $color{#4257b2}M=N$.

$$
log_{2} x=log_{2} 25
$$

$$
x=25
$$

So the solution of the equation is $boxed{ x=25 }$

(b) We would like to solve the equation $color{#4257b2}log_{3} x=4log_{3} 3$. First, we note that the right side is a logarithm which is multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{m} x=log_{m} x^{r}$.

$$
log_{3} x=4log_{3} 3
$$

$$
log_{3} x=log_{3} 3^{4}
$$

$$
log_{3} x=log_{3} 81
$$

Now we note that the two side each of them is a logarithm with the base $color{#4257b2}3$, so the the two expressions must equal each other because we know that if $color{#4257b2}log_{a} M=log_{a} N$, then $color{#4257b2}M=N$.

$$
log_{3} x=log_{3} 81
$$

$$
x=81
$$

So the solution of the equation is $boxed{ x=81 }$

(c) We would like to solve the equation $color{#4257b2}log x=3log 2$. First, we note that the right side is a logarithm which is multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{m} x=log_{m} x^{r}$.

$$
log x=3log 2
$$

$$
log x=log_{2} 2^{3}
$$

$$
log x=log 8
$$

Now we note that the two side each of them is a logarithm with the base $color{#4257b2}10$, so the the two expressions must equal each other because we know that if $color{#4257b2}log_{a} M=log_{a} N$, then $color{#4257b2}M=N$.

$$
log x=log 8
$$

$$
x=8
$$

So the solution of the equation is $boxed{ x=8 }$

(d) We would like to solve the equation $color{#4257b2}log (x-5)=log 10$. First, we note that the two side each of them is a logarithm with the base $color{#4257b2}10$, so the the two expressions must equal each other because we know that if $color{#4257b2}log_{a} M=log_{a} N$, then $color{#4257b2}M=N$.

$$
log (x-5)=log 10
$$

$$
x-5=10
$$

Now we can add $color{#4257b2}5$ to each side to make the left side contains the variable $color{#4257b2}x$ only.

$$
x-5+5=10+5
$$

$$
x=15
$$

So the solution of the equation is $boxed{ x=15 }$

(e) We would like to solve the equation $color{#4257b2}log_{2} 8=x$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{2} 8=x
$$

$$
2^{x}=8
$$

But we know that $color{#4257b2}8=2^{3}$, so we can use this fact to replace $color{#4257b2}8$ from the right side $color{#4257b2}2^{3}$.

$$
2^{x}=2^{3}
$$

Now we note that the two sides each of them is an exponential function and have the same base, so the exponent of the left side must equal the exponent of the right side where we know that if $color{#4257b2}x^{a}=x^{b}$, then $color{#4257b2}a=b$.

$$
2^{x}=2^{3}
$$

$$
x=3
$$

So the solution of the equation is $boxed{ x=3 }$

(f) We would like to solve the equation $color{#4257b2}log_{2} x=dfrac{1}{2} log_{2} 3$. First, we note that the right side is a logarithm which is multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{m} x=log_{m} x^{r}$.

$$
log_{2} x=dfrac{1}{2} log_{2} 3
$$

$$
log_{2} x=log_{2} 3^{frac{1}{2}}
$$

$$
log_{2} x=log_{2} sqrt{3}
$$

Now we note that the two side each of them is a logarithm with the base $color{#4257b2}2$, so the the two expressions must equal each other because we know that if $color{#4257b2}log_{a} M=log_{a} N$, then $color{#4257b2}M=N$.

$$
log_{2} x=log_{2} sqrt{3}
$$

$$
x=sqrt{3}
$$

So the solution of the equation is $boxed{ x=sqrt{3} }$

Large{$text{color{#c34632}(a) $x=25$ (c) $x=8$ (e) $x=3$
\
\
(b) $x=81$ (d) $x=15$ (f) $x=sqrt{3}$}$

(a) We would like to solve the equation $color{#4257b2}log_{x} 625=4$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{x} 625=4
$$

$$
x^{4}=625
$$

But we know that $color{#4257b2}625=5^{4}$, so we can use this fact to replace $color{#4257b2}625$ from the right side $color{#4257b2}5^{4}$.

$$
x^{4}=5^{4}
$$

Now we note that the two sides each of them is an exponential function and have the same exponent, so the base of the left side must equal the base of the right side where we know that if $color{#4257b2}a^{x}=b^{x}$, then $color{#4257b2}a=b$.

$$
x^{4}=5^{4}
$$

$$
x=5
$$

So the solution of the equation is $boxed{ x=5 }$

(b) We would like to solve the equation $color{#4257b2}log_{x} 6=-dfrac{1}{2}$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{x} 6=-dfrac{1}{2}
$$

$$
x^{-frac{1}{2}}=6
$$

Now we can use the property of exponents $color{#4257b2}x^{-a}=dfrac{1}{x^{a}}$ to simplify the left side.

$$
dfrac{1}{x^{frac{1}{2}}}=6
$$

$$
dfrac{1}{sqrt{x}}=6
$$

Note that we know that $color{#4257b2}sqrt{x}=x^{frac{1}{2}}$, so we replaced $color{#4257b2}x^{frac{1}{2}}$ by $color{#4257b2}sqrt{x}$. Now we can square the two sides to eliminate the square root in the left side.

$$
left(dfrac{1}{sqrt{x}}right)^{2}=6^{2}
$$

$$
dfrac{1}{x}=36
$$

$$
x=dfrac{1}{36}
$$

So the solution of the equation is $boxed{ x=dfrac{1}{36} }$

(c) We would like to solve the equation $color{#4257b2}log_{5} (2x-1)=2$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
log_{5} (2x-1)=2
$$

$$
2x-1=5^{2}
$$

$$
2x-1=25
$$

Now we can add $color{#4257b2}1$ to each side.

$$
2x-1+1=25+1
$$

$$
2x=26
$$

Now we can divide the two sides by $color{#4257b2}2$ to find the value of $color{#4257b2}x$.

$$
dfrac{2x}{2}=dfrac{26}{2}
$$

$$
x=13
$$

So the solution of the equation is $boxed{ x=13 }$

(d) We would like to solve the equation $color{#4257b2}log (5x-2)=3$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log x=b$, then $color{#4257b2}x=10^{b}$.

$$
log (5x-2)=3
$$

$$
5x-2=10^{3}
$$

$$
5x-2=1000
$$

Now we can add $color{#4257b2}2$ to each side.

$$
5x-2+2=1000+2
$$

$$
5x=1002
$$

Now we can divide the two sides by $color{#4257b2}5$ to find the value of $color{#4257b2}x$.

$$
dfrac{5x}{5}=dfrac{1002}{5}
$$

$$
x=200.4
$$

So the solution of the equation is $boxed{ x=200.4 }$

(e) We would like to solve the equation $color{#4257b2}log_{x} 0.04=-2$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{x} 0.04=-2
$$

$$
x^{-2}=0.04
$$

$$
x^{-2}=dfrac{1}{25}
$$

But we know that $color{#4257b2}25=5^{2}$, so we can use this fact to replace $color{#4257b2}25$ from the right side $color{#4257b2}5^{2}$.

$$
x^{-2}=dfrac{1}{5^{2}}
$$

Now we can use the property of exponents $color{#4257b2}dfrac{1}{x^{a}}=x^{-a}$ to replace $color{#4257b2}dfrac{1}{5^{2}}$ by $color{#4257b2}5^{-2}$.

$$
x^{-2}=dfrac{1}{5^{2}}
$$

$$
x^{-2}=5^{-2}
$$

Now we note that the two sides each of them is an exponential function and have the same exponent, so the base of the left side must equal the base of the right side where we know that if $color{#4257b2}a^{x}=b^{x}$, then $color{#4257b2}a=b$.

$$
x^{-2}=5^{-2}
$$

$$
x=5
$$

So the solution of the equation is $boxed{ x=5 }$

(f) We would like to solve the equation $color{#4257b2}log_{5} (2x-4)=log_{5} 36$. First, we note that the two side each of them is a logarithm with the base $color{#4257b2}5$, so the the two expressions must equal each other because we know that if $color{#4257b2}log_{a} M=log_{a} N$, then $color{#4257b2}M=N$.

$$
log_{5} (2x-4)=log_{5} 36
$$

$$
2x-4=36
$$

Now we can add $color{#4257b2}4$ to each side.

$$
2x-4+4=36+4
$$

$$
2x=40
$$

Now we can divide the two sides by $color{#4257b2}2$ to find the value of $color{#4257b2}x$.

$$
dfrac{2x}{2}=dfrac{40}{2}
$$

$$
x=20
$$

So the solution of the equation is $boxed{ x=20 }$

Large{$text{color{#c34632}(a) $x=5$ (c) $x=13$ (e) $x=5$
\
\
(b) $x=dfrac{1}{36}$ (d) $x=200.4$ (f) $x=20$}$

We would like to determine the value of $color{#4257b2}a$ in the given formula
$color{#4257b2}R=logleft(dfrac{a}{T}right)+B$ if we know that $color{#4257b2}R=6.3, B=4.2$ and $color{#4257b2}T=1.6$. First, we will substitute these values in the formula and then simplify to find the value of $color{#4257b2}a$.

$$
R=logleft(dfrac{a}{T}right)+B
$$

$$
6.3=logleft(dfrac{a}{1.6}right)+4.2
$$

Now we can subtract $color{#4257b2}4.2$ from each side.

$$
6.3-4.2=logleft(dfrac{a}{1.6}right)+4.2-4.2
$$

$$
2.1=logleft(dfrac{a}{1.6}right)
$$

Now we can convert form the logarithmic form to the exponential form where we know that if $color{#4257b2}log x=a$, then $color{#4257b2}x=10^{a}$.

$$
dfrac{a}{1.6}=10^{2.1}
$$

$$
dfrac{a}{1.6}=125.9
$$

Now we can multiply the two sides by $color{#4257b2}1.6$ to make $color{#4257b2}a$ in the left side alone.

$$
left(1.6right)cdot left(dfrac{a}{1.6}right)=(1.6)cdot (125.9)
$$

$$
cancel{left(1.6right)}cdot left(dfrac{a}{cancel{1.6}}right)=(1.6)cdot (125.9)
$$

$$
a=201.43
$$

So the value of $color{#4257b2}a$ is $boxed{ a=201.43 }$

Large{$text{color{#c34632}$a=201.43$}$

(a) We would like to solve the equation $color{#4257b2}log_{x} 27=dfrac{3}{2}$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{x} 27=dfrac{3}{2}
$$

$$
x^{frac{3}{2}}=27
$$

$$
x^{left(frac{1}{2}right)cdot (3)}=27
$$

Note that we split the exponent $color{#4257b2}dfrac{3}{2}$ to two multiplied exponents because in this case we can use the property of exponents $color{#4257b2}x^{acdot b}=(x^{a})^{b}$ as follows:

$$
x^{left(frac{1}{2}right)cdot (3)}=27
$$

$$
left(x^{frac{1}{2}}right)^{3}=27
$$

$$
left(sqrt{x}right)^{3}=27
$$

But we know that $color{#4257b2}27=3^{3}$, so we can use this fact to replace $color{#4257b2}27$ from the right side $color{#4257b2}3^{3}$.

$$
left(sqrt{x}right)^{3}=(3)^{3}
$$

Now we note that the two sides each of them is an exponential function and have the same exponent, so the base of the left side must equal the base of the right side where we know that if $color{#4257b2}a^{x}=b^{x}$, then $color{#4257b2}a=b$.

$$
left(sqrt{x}right)^{3}=(3)^{3}
$$

$$
sqrt{x}=3
$$

Now we can square the two sides to eliminate the square root from the left side.

$$
left(sqrt{x}right)^{2}=3^{2}
$$

$$
x=9
$$

So the solution of the equation is $boxed{ x=9 }$

(b) We would like to solve the equation $color{#4257b2}log_{x} 5=2$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{x} 5=2
$$

$$
x^{2}=5
$$

Now we can take the square root for each side to find the value of $color{#4257b2}x$.

$$
x=pm sqrt{5}
$$

But we know that if $color{#4257b2}log_{a} x=b$, so $color{#4257b2}a$ and $color{#4257b2}x$ must be positive, so the solution of $color{#4257b2}x=-sqrt{5}$ is refused.

$$
x=sqrt{5}
$$

So the solution of the equation is $boxed{ x=sqrt{5} }$

(c) We would like to solve the equation $color{#4257b2}log_{3} (3x+2)=3$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
log_{3} (3x+2)=3
$$

$$
3x+2=3^{3}
$$

$$
3x+2=27
$$

Now we can subtract $color{#4257b2}2$ from each side.

$$
3x+2-2=27-2
$$

$$
3x=25
$$

Now we can divide the two sides by $color{#4257b2}3$ to find the value of $color{#4257b2}x$.

$$
dfrac{3x}{3}=dfrac{25}{3}
$$

$$
x=dfrac{25}{3}
$$

So the solution of the equation is $boxed{ x=dfrac{25}{3} }$

(d) We would like to solve the equation $color{#4257b2}log x=4$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log x=a$, then $color{#4257b2}x=10^{a}$.

$$
log x=4
$$

$$
x=10^{4}
$$

$$
x=10000
$$

So the solution of the equation is $boxed{ x=10000 }$

(e) We would like to solve the equation $color{#4257b2}log_{frac{1}{3}} 27=x$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}a^{b}=x$.

$$
log_{frac{1}{3}} 27=x
$$

$$
left(dfrac{1}{3}right)^{x}=27
$$

Now we can use the property of exponent $color{#4257b2}dfrac{1}{x^{a}}=x^{-a}$ to replace $color{#4257b2}dfrac{1}{3}$ from the left side by $color{#4257b2}3^{-1}$.

$$
(3^{-1})^{x}=27
$$

Now we can use the property of exponents $color{#4257b2}(x^{a})^{b}=x^{acdot b}$ as follows:

$$
(3^{-1})^{x}=27
$$

$$
3^{(-1)cdot (x)}=27
$$

$$
(3)^{-x}=27
$$

But we know that $color{#4257b2}27=3^{3}$, so we can use this fact to replace $color{#4257b2}27$ from the right side $color{#4257b2}3^{3}$.

$$
(3)^{-x}=(3)^{3}
$$

Now we note that the two sides each of them is an exponential function and have the same base, so the exponent of the left side must equal the exponent of the right side where we know that if $color{#4257b2}x^{a}=x^{b}$, then $color{#4257b2}a=b$.

$$
(3)^{-x}=(3)^{3}
$$

$$
-x=3
$$

Now we can divide the two sides by $color{#4257b2}-1$ to find the value of $color{#4257b2}x$.

$$
dfrac{-x}{-1}=dfrac{3}{-1}
$$

$$
x=-3
$$

So the solution of the equation is $boxed{ x=-3 }$

(f) We would like to solve the equation $color{#4257b2}log_{frac{1}{2}} x=-2$. First, we can convert our equation from the logarithm form to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
log_{frac{1}{2}} x=-2
$$

$$
x=left(dfrac{1}{2}right)^{-2}
$$

$$
x=dfrac{(1)^{-2}}{(2)^{-2}}
$$

$$
x=dfrac{1}{(2)^{-2}}
$$

Now we can use the property of exponent $color{#4257b2}dfrac{1}{x^{-a}}=x^{a}$ to replace $color{#4257b2}dfrac{1}{2^{-2}}$ from the left side by $color{#4257b2}2^{2}$.

$$
x=dfrac{1}{(2)^{-2}}
$$

$$
x=2^{2}
$$

$$
x=4
$$

So the solution of the equation is $boxed{ x=4 }$

Large{$text{color{#c34632}(a) $x=9$ (c) $x=dfrac{25}{3}$ (e) $x=-3$
\
\
(b) $x=sqrt{5}$ (d) $x=10000$ (f) $x=4$}$

(a) We would like to solve the equation $color{#4257b2}log_{2} x+log_{2} 3=3$. First, we note that the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log_{2} x+log_{2} 3=3
$$

$$
log_{2} (x)(3)=3
$$

$$
log_{2} 3x=3
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
3x=2^{3}
$$

$$
3x=8
$$

Now we can divide the two sides by $color{#4257b2}3$ to find the value of $color{#4257b2}x$.

$$
dfrac{3x}{3}=dfrac{8}{3}
$$

$$
x=dfrac{8}{3}
$$

So the solution of the equation is $boxed{ x=dfrac{8}{3} }$

(b) We would like to solve the equation $color{#4257b2}log 3+log x=1$. First, we note that the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log 3+log x=1
$$

$$
log (3)(x)=1
$$

$$
log 3x=1
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log x=b$, then $color{#4257b2}x=10^{b}$.

$$
3x=10^{1}
$$

$$
3x=10
$$

Now we can divide the two sides by $color{#4257b2}3$ to find the value of $color{#4257b2}x$.

$$
dfrac{3x}{3}=dfrac{10}{3}
$$

$$
x=dfrac{10}{3}
$$

So the solution of the equation is $boxed{ x=dfrac{10}{3} }$

(c) We would like to solve the equation $color{#4257b2}log_{5} 2x+dfrac{1}{2} log_{5} 9=2$. First, we note that the second term in the left side is a logarithm which is multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{m} x=log_{m} x^{r}$.

$$
log_{5} 2x+dfrac{1}{2} log_{5} 9=2
$$

$$
log_{5} 2x+log_{5} 9^{frac{1}{2}}=2
$$

$$
log_{5} 2x+log_{5} sqrt{9}=2
$$

$$
log_{5} 2x+log_{5} 3=2
$$

Now we note that the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log_{5} (2x)(3)=2
$$

$$
log_{5} 6x=2
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
6x=5^{2}
$$

$$
6x=25
$$

Now we can divide the two sides by $color{#4257b2}6$ to find the value of $color{#4257b2}x$.

$$
dfrac{6x}{6}=dfrac{25}{6}
$$

$$
x=dfrac{25}{6}
$$

So the solution of the equation is $boxed{ x=dfrac{25}{6} }$

(d) We would like to solve the equation $color{#4257b2}log_{4} x-log_{4} 2=2$. First, we note that the left side is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
log_{4} x-log_{4} 2=2
$$

$$
log_{4} left(dfrac{x}{2}right)=2
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
dfrac{x}{2}=4^{2}
$$

$$
dfrac{x}{2}=16
$$

Now we can multiply the two sides by $color{#4257b2}2$ to find the value of $color{#4257b2}x$.

$$
(2)cdot left(dfrac{x}{2}right)=(16)cdot(2)
$$

$$
x=32
$$

So the solution of the equation is $boxed{ x=32 }$

(e) We would like to solve the equation $color{#4257b2}3log x-log 3=2log 3$. First, we can add $color{#4257b2}log 3$ to each side.

$$
3log x-log 3=2log 3
$$

$$
3log x-log 3+log 3=2log 3+log 3
$$

$$
3log xcancel{-log 3}cancel{+log 3}=2log 3+log 3
$$

$$
3log x=2log 3+log 3
$$

Now we note that the right side is a sum of two logarithms have the same base and expression, so we can add them directly.

$$
3log x=3log 3
$$

Now we can divide the two sides by $color{#4257b2}3$.

$$
dfrac{3log x}{3}=dfrac{3log 3}{3}
$$

$$
log x=log 3
$$

Now we note that the two sides each of them is a logarithm with the same base, so the two expressions must equal each other because we know that if $color{#4257b2}log_{a} M=log_{a} N$, then $color{#4257b2}M=N$.

$$
x=3
$$

So the solution of the equation is $boxed{ x=3 }$

(f) We would like to solve the equation $color{#4257b2}log_{3} 4x+log_{3} 5-log_{3} 2=4$. First, we note that the first two terms in the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log_{3} 4x+log_{3} 5-log_{3} 2=4
$$

$$
left(log_{3} 4x+log_{3} 5right)-log_{3} 2=4
$$

$$
log_{3} [(4x)cdot (5)]-log_{3} 2=4
$$

$$
log_{3} 20x-log_{3} 2=4
$$

Now we note that the left side is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
log_{3} 20x-log_{3} 2=4
$$

$$
log_{3} left(dfrac{20x}{2}right)=4
$$

$$
log_{3} 10x=4
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
log_{3} 10x=4
$$

$$
10x=3^{4}
$$

$$
10x=81
$$

Now we can divide the two sides by $color{#4257b2}10$ to find the value of $color{#4257b2}x$.

$$
dfrac{10x}{10}=dfrac{81}{10}
$$

$$
x=8.1
$$

So the solution of the equation is $boxed{ x=8.1 }$

Large{$text{color{#c34632}(a) $x=dfrac{8}{3}$ (c) $x=dfrac{25}{6}$ (e) $x=3$
\
\
(b) $x=dfrac{10}{3}$ (d) $x=32$ (f) $x=8.1$}$

We would like to solve the equation $color{#4257b2}log_{6} x+log_{6} (x-5)=2$. First, we note that the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log_{6} x+log_{6} (x-5)=2
$$

$$
log_{6} x(x-5)=2
$$

$$
log_{6} (x^{2}-5x)=2
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
log_{6} (x^{2}-5x)=2
$$

$$
x^{2}-5x=6^{2}
$$

$$
x^{2}-5x=36
$$

Now we can subtract $color{#4257b2}36$ from each side to make the right side equals zero.

$$
x^{2}-5x-36=0
$$

Now we have a quadratic equation, so we can factor it to find the values of $color{#4257b2}x$.

$$
(x-9)(x+4)=0
$$

Now we can use the zero-factor property.

$$
x-9=0 text{or} x+4=0
$$

$$
x=9 text{or} x=-4
$$

Now we found two solutions for $color{#4257b2}x$, so the next step is to check these values in the original equation to know if they verify it or not.

For $color{#4257b2}x=9$

$$
log_{6} x+log_{6} (x-5)=2
$$

$$
log_{6} 9+log_{6} (9-5)=2
$$

$$
log_{6} 9+log_{6} 4=2
$$

$$
1.226+.0774=2
$$

$$
2=2
$$

So the solution $color{#4257b2}x=9$ is true because it verifies the original equation.

For $color{#4257b2}x=-4$

$$
log_{6} x+log_{6} (x-5)=2
$$

$$
log_{6} -4+log_{6} (-4-5)=2
$$

$$
log_{6} -4+log_{6} -9=2
$$

But we know that $color{#4257b2}log_{6} -9$ is undefined because the number inside the logarithm must be positive, so the solution $color{#4257b2}x=-4$ is false because it doesn’t verify the original equation.

So the solution of the equation is $boxed{ x=9 }$

$$
color{#c34632}x=9
$$

(a) We would like to solve the equation $color{#4257b2}log_{7} (x+1)+log_{7} (x-5)=1$. First, we note that the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log_{7} (x+1)+log_{7} (x-5)=1
$$

$$
log_{7} (x+1)(x-5)=1
$$

$$
log_{7} (x^{2}-4x-5)=1
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
x^{2}-4x-5=7^{1}
$$

$$
x^{2}-4x-5=7
$$

Now we can subtract $color{#4257b2}7$ from each side to make the right side equals zero.

$$
x^{2}-4x-5-7=0
$$

$$
x^{2}-4x-12=0
$$

Now we have a quadratic equation, so we can factor it to find the values of $color{#4257b2}x$.

$$
(x-6)(x+2)=0
$$

Now we can use the zero-factor property.

$$
x-6=0 text{or} x+2=0
$$

$$
x=6 text{or} x=-2
$$

Now we found two solutions for $color{#4257b2}x$, so the next step is to check these values in the original equation to know if they verify it or not.

For $color{#4257b2}x=6$

$$
log_{7} (x+1)+log_{7} (x-5)=1
$$

$$
log_{7} (6+1)+log_{7} (6-5)=1
$$

$$
log_{7} 7+log_{7} 1=1
$$

$$
1+0=1
$$

$$
1=1
$$

So the solution $color{#4257b2}x=6$ is true because it verifies the original equation.

For $color{#4257b2}x=-2$

$$
log_{7} (x+1)+log_{7} (x-5)=1
$$

$$
log_{7} (-2+1)+log_{7} (-2-5)=1
$$

$$
log_{7} -1+log_{7} -7=1
$$

But we know that $color{#4257b2}log_{7} -1$ and $color{#4257b2}log_{7} -7$ are undefined because the number inside the logarithm must be positive, so the solution $color{#4257b2}x=-2$ is false because it doesn’t verify the original equation.

So the solution of the equation is $boxed{ x=6 }$

(b) We would like to solve the equation $color{#4257b2}log_{3} (x-2)+log_{3} x=1$. First, we note that the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log_{3} (x-2)+log_{3} x=1
$$

$$
log_{3} x(x-2)=1
$$

$$
log_{3} (x^{2}-2x)=1
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
log_{3} (x^{2}-2x)=1
$$

$$
x^{2}-2x=3^{1}
$$

$$
x^{2}-2x=3
$$

Now we can subtract $color{#4257b2}3$ from each side to make the right side equals zero.

$$
x^{2}-2x-3=0
$$

Now we have a quadratic equation, so we can factor it to find the values of $color{#4257b2}x$.

$$
(x-3)(x+1)=0
$$

Now we can use the zero-factor property.

$$
x-3=0 text{or} x+1=0
$$

$$
x=3 text{or} x=-1
$$

Now we found two solutions for $color{#4257b2}x$, so the next step is to check these values in the original equation to know if they verify it or not.

For $color{#4257b2}x=3$

$$
log_{3} (x-2)+log_{3} x=1
$$

$$
log_{3} (3-2)+log_{3} 3=1
$$

$$
log_{3} 1+log_{3} 3=1
$$

$$
0+1=1
$$

$$
1=1
$$

So the solution $color{#4257b2}x=3$ is true because it verifies the original equation.

For $color{#4257b2}x=-1$

$$
log_{3} (x-2)+log_{3} x=1
$$

$$
log_{3} (-1-2)+log_{3} -1=1
$$

$$
log_{3} -3+log_{3} -1=1
$$

But we know that $color{#4257b2}log_{3} -3$ and $color{#4257b2}log_{3} -1$ are undefined because the number inside the logarithm must be positive, so the solution $color{#4257b2}x=-1$ is false because it doesn’t verify the original equation.

So the solution of the equation is $boxed{ x=3 }$

(c) We would like to solve the equation $color{#4257b2}log_{6} x-log_{6} (x-1)=1$. First, we note that the left side is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
log_{6} x-log_{6} (x-1)=1
$$

$$
log_{6} left(dfrac{x}{x-1}right)=1
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
log_{6} left(dfrac{x}{x-1}right)=1
$$

$$
dfrac{x}{x-1}=6^{1}
$$

$$
dfrac{x}{x-1}=6
$$

Now we can multiply the two sides by $color{#4257b2}x-1$ eliminate the denominator in the left side.

$$
(x-1)cdot left(dfrac{x}{x-1}right)=6(x-1)
$$

$$
cancel{(x-1)}cdot left(dfrac{x}{cancel{x-1}}right)=6x-6
$$

$$
x=6x-6
$$

Now we can subtract $color{#4257b2}6x$ from each side to make the variable $color{#4257b2}x$ in the left side alone.

$$
x-6x=-6
$$

$$
-5x=-6
$$

Now we can divide the two sides by $color{#4257b2}-5$.

$$
x=dfrac{-6}{-5}=dfrac{6}{5}=1.2
$$

Now we found one solution for $color{#4257b2}x$, so the next step is to check this value in the original equation to know if they verify it or not.

For $color{#4257b2}x=1.2$

$$
log_{6} x-log_{6} (x-1)=1
$$

$$
log_{6} 1.2-log_{6} left(1.2-1right)=1
$$

$$
log_{6} 1.2-log_{6} 0.2=1
$$

$$
0.102-(-0.898)=1
$$

$$
1=1
$$

So the solution $color{#4257b2}x=1.2$ is true because it verifies the original equation.

So the solution of the equation is $boxed{ x=1.2 }$

(d) We would like to solve the equation $color{#4257b2}log (2x+1)+log (x-1)=log 9$. First, we note that the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log (2x+1)+log (x-1)=log 9
$$

$$
log (2x+1)(x-1)=log 9
$$

$$
log (2x^{2}-x-1)=log 9
$$

Now we note that the two sides each of them is a logarithm with the same base, so the two expressions must equal each other because we know that if $color{#4257b2}log_{a} M=log_{a} N$, then $color{#4257b2}M=N$.

$$
2x^{2}-x-1=9
$$

Now we can subtract $color{#4257b2}9$ from each side to make the right side equals zero.

$$
2x^{2}-x-1-9=0
$$

$$
2x^{2}-x-10=0
$$

Now we have a quadratic equation, so we can factor it to find the values of $color{#4257b2}x$.

$$
(2x-5)(x+2)=0
$$

Now we can use the zero-factor property.

$$
2x-5=0 text{or} x+2=0
$$

$$
x=dfrac{5}{2}=2.5 text{or} x=-2
$$

Now we found two solutions for $color{#4257b2}x$, so the next step is to check these values in the original equation to know if they verify it or not.

For $color{#4257b2}x=2.5$

$$
log (2x+1)+log (x-1)=log 9
$$

$$
log (2(2.5)+1)+log (2.5-1)=log 9
$$

$$
log 6+log 1.5=log 9
$$

$$
0.778+0.176=0.954
$$

$$
0.954=0.954
$$

So the solution $color{#4257b2}x=2.5$ is true because it verifies the original equation.

For $color{#4257b2}x=-2$

$$
log (2x+1)+log (x-1)=log 9
$$

$$
log (2(-2)+1)+log (-2-1)=log 9
$$

$$
log -3+log -3=log 9
$$

But we know that $color{#4257b2}log -3$ is undefined because the number inside the logarithm must be positive, so the solution $color{#4257b2}x=-2$ is false because it doesn’t verify the original equation.

So the solution of the equation is $boxed{ x=2.5 }$

(e) We would like to solve the equation $color{#4257b2}log (x+2)+log (x-1)=1$. First, we note that the left side is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
log (x+2)+log (x-1)=1
$$

$$
log (x+2)(x-1)=1
$$

$$
log (x^{2}+x-2)=1
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
x^{2}+x-2=10^{1}
$$

$$
x^{2}+x-2=10
$$

Now we can subtract $color{#4257b2}10$ from each side to make the right side equals zero.

$$
x^{2}+x-2-10=0
$$

$$
x^{2}+x-12=0
$$

Now we have a quadratic equation, so we can factor it to find the values of $color{#4257b2}x$.

$$
(x-3)(x+4)=0
$$

Now we can use the zero-factor property.

$$
x-3=0 text{or} x+4=0
$$

$$
x=3 text{or} x=-4
$$

Now we found two solutions for $color{#4257b2}x$, so the next step is to check these values in the original equation to know if they verify it or not.

For $color{#4257b2}x=3$

$$
log (x+2)+log (x-1)=1
$$

$$
log (3+2)+log (3-1)=1
$$

$$
log 5+log 2=1
$$

$$
0.7+0.3=1
$$

$$
1=1
$$

So the solution $color{#4257b2}x=3$ is true because it verifies the original equation.

For $color{#4257b2}x=-4$

$$
log (x+2)+log (x-1)=1
$$

$$
log (-4+2)+log (-4-1)=1
$$

$$
log -2+log -5=1
$$

But we know that $color{#4257b2}log -2$ and $color{#4257b2}log -5$ are undefined because the number inside the logarithm must be positive, so the solution $color{#4257b2}x=-4$ is false because it doesn’t verify the original equation.

So the solution of the equation is $boxed{ x=3 }$

(f) We would like to solve the equation $color{#4257b2}3log_{2} x-log_{2} x=8$. First, we note that the left side is a difference of two logarithms have the same base and expression, so we can subtract them directly.

$$
3log_{2} x-log_{2} x=8
$$

$$
2log_{2} x=8
$$

Now we note that the left side is a logarithm which is multiplied by a number, so we can use the power law of logarithms where $color{#4257b2}r log_{m} x=log_{m} x^{r}$.

$$
2log_{2} x=8
$$

$$
log_{2} x^{2}=8
$$

Now we have an equation on the logarithmic form, so we can convert it to the exponential form where we know that if $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x=a^{b}$.

$$
x^{2}=2^{8}
$$

$$
x^{2}=256
$$

Now we can take the square root for each side to find the value of $color{#4257b2}x$.

$$
x=pm sqrt{256}=pm16
$$

But we know that when $color{#4257b2}log_{a} x=b$, then $color{#4257b2}x$ must be positive, so the solution $color{#4257b2}x=-16$ is refused because in this case the original equation will contains $color{#4257b2}log_{2} -16$ which is undefined.

$$
x=16
$$

So the solution of the equation is $boxed{ x=16 }$

Large{$text{color{#c34632}(a) $x=6$ (c) $x=1.2$ (e) $x=3$
\
\
(b) $x=3$ (d) $x=2.5$ (f) $x=16$}$

Describe the strategy that would you use to solve the following equations.

$$
color{#4257b2}text{(a)} log_9(x)=log_9(4)+log_9(5)
$$

First, to solve the logarithmic equation, you should simplify the equation by using the different laws, its included but not limited to:

$$
log_a(x)+log_a(y)=log_a(xcdot y)
$$

When the both of sides in the equation has the same base of the logarithmic, so we use the following standard form:

$$
because log_a(x)=log_a(y) therefore x=y
$$

$$
color{#4257b2}text{(b)} log(x)-log(2)=3
$$

First, to solve the logarithmic equation, you should simplify the equation by using the different laws, its included but not limited to:

$$
log_a(x)-log_a(y)=log_aleft(dfrac{x}{y}right)
$$

When the both of sides in the equation has the same base of the logarithmic, so we use the following standard form:

$$
because log_a(x)=log_a(y) therefore x=y
$$

$$
color{#4257b2}text{(c)} log(x)=2log(8)
$$

First, to solve the logarithmic equation, you should simplify the equation by using the different laws, its included but not limited to:

$$
log_a(x)-log_a(y)=log_aleft(dfrac{x}{y}right)
$$

When only side in the equation has the a logarithmic with base number $(10)$, so we use the exponential form as follows:

$$
because log_{10}(x)=b therefore x=10^b
$$

$$
text{color{#c34632}Large See the description}
$$

Determine the following terms if the $L=10logleft(dfrac{I}{I_{o}}right)$, where:
$I_{o}=10^{-12}$ W/m$^2$
$I$, is the intensity of the sound, W/m$^2$
$L$, is the loudness of sound in desible

$$
text{color{#4257b2}(a) Determine the intensity of the teacher if the sound level is $50$ dB}
$$

$$
L=10logleft(dfrac{I}{I_{o}}right) 50=10logleft(dfrac{I}{10^{-12}}right)
$$

Divide both of sides by $(10)$ as follows:

$$
5=logleft(dfrac{I}{10^{-12}}right)
$$

Use the exponential standard form as follows:

$$
because log_{10}(x)=b x=10^b
$$

$$
therefore left(dfrac{I}{10^{-12}}right)=10^5
$$

Isolate the $(I)$ in the left side as follows:

$$
I=10^5cdot10^{-12} I=10^{5-12}
$$

$$
I=10^{-7} text{W/m}^2
$$

$$
text{color{#4257b2}(b) Determine the intensity of the music of an MP3 player if the sound level is $84$ dB}
$$

$$
L=10logleft(dfrac{I}{I_{o}}right) 84=10logleft(dfrac{I}{10^{-12}}right)
$$

Divide both of sides by $(10)$ as follows:

$$
8.4=logleft(dfrac{I}{10^{-12}}right)
$$

Use the exponential standard form as follows:

$$
because log_{10}(x)=b x=10^b
$$

$$
therefore left(dfrac{I}{10^{-12}}right)=10^8.4
$$

Isolate the $(I)$ in the left side as follows:

$$
I=10^{8.4}cdot10^{-12} I=10^{8.4-12}
$$

$$
I=10^{-3.6} text{W/m}^2
$$

$$
text{color{#c34632}(a) $I=10^{-7} text{W/m}^2$ (b) $I=10^{-3.6} text{W/m}^2$}
$$

Solve the following expression.

$$
color{#4257b2}text{(a)} log_a(x+2)+log_a(x-1)=log_a(8-2x)
$$

Use standard form as follows:

$$
because log_a(x)+log_a(y)=log_a(xcdot y)
$$

$$
therefore log_a(x+2)+log_a(x-1)=log_a(8-2x) log_a[(x+2)(x-1)]=log_a(8-2x)
$$

$$
log_a(x^2+x-2)=log_a(8-2x)
$$

Use standard form as follows:

$$
because log_a(x)=log_a(y) therefore x=y
$$

$$
because log_a(x^2+x-2)=log_a(8-2x) therefore x^2+x-2=8-2x
$$

Rearrange the tiles to group like terms as follows:

$$
x^2+(x+2x)+(-2-8)=0 x^2+3x-10=0
$$

$$
(x-2)(x+5)=0 x=2 text{or} x=-5
$$

$text{color{#4257b2}Check:}$ Use the values of $x$ in the equation as follows:

$$
text{color{#4257b2}For $(x=2)$}
$$

$$
log_a(x+2)+log_a(x-1)=log_a(8-2x) log_a(2+2)+log_a(2-1)=log_a(8-(2cdot2))
$$

$$
log_a(4)+log_a(1)=log_a(4) log_a(4cdot1)=log_a(4)
$$

$$
log_a(4)=log_a(4)
$$

Since the left side is equal the right side, so the answer is correct.

$$
text{color{#4257b2}For $(x=-5)$}
$$

$$
log_a(x+2)+log_a(x-1)=log_a(8-2x) log_a(-5+2)+log_a(-5-1)=log_a(8-(2cdot-5))
$$

$$
log_a(-3)+log_a(-6)=log_a(18) log_a(-3cdot-6)=log_a(18)
$$

$$
log_a(18)=log_a(18)
$$

Since the left side is equal the right side, so the answer is correct.

$$
text{color{#c34632}$x=2$ or $x=-5$}
$$

Use graphing technology to solve the following expression.

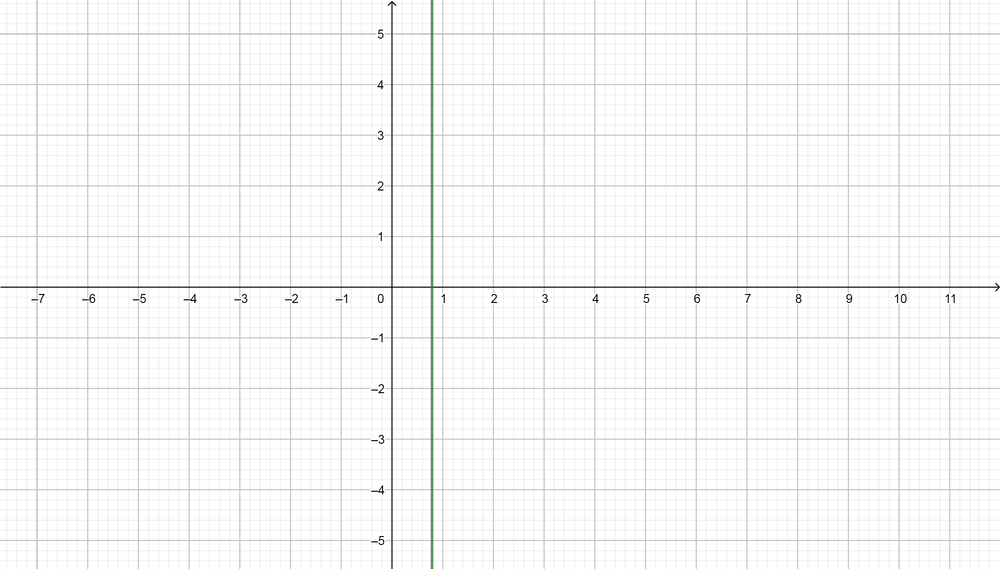
$$
color{#4257b2}text{(a)} log(x+3)=log(7-4x)
$$

From the graph $(x=0.8)$

$$
color{#4257b2}text{(b)} 5^x=3^{x+1}
$$

From the graph $(x=2.15)$

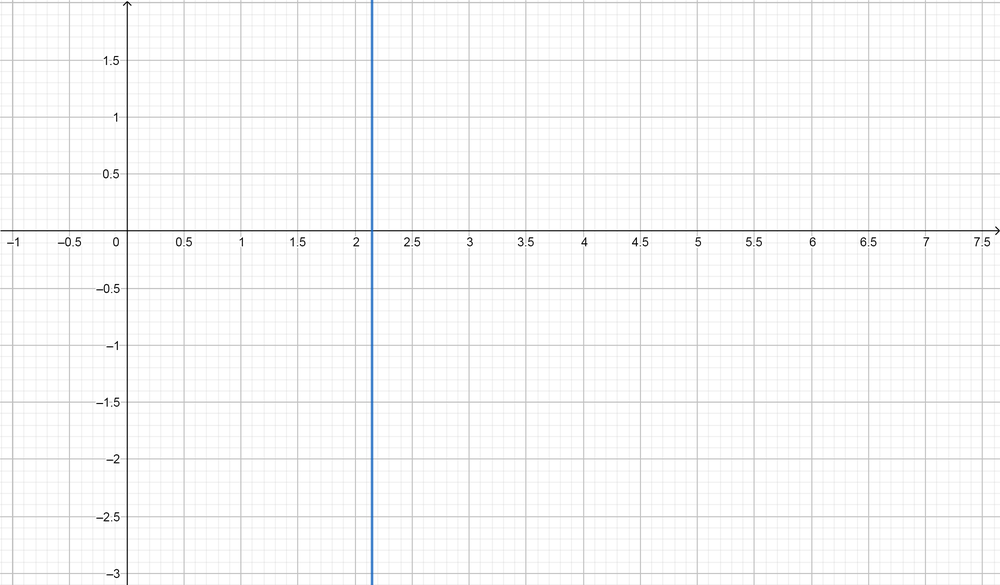
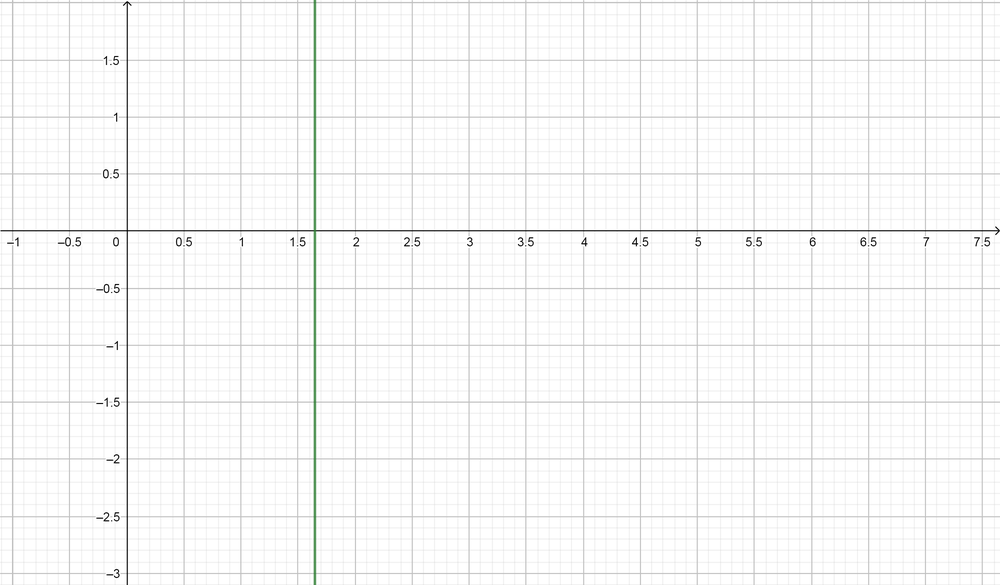
$$
color{#4257b2}text{(c)} 2log(x)=1
$$

From the graph $(x=1.64)$

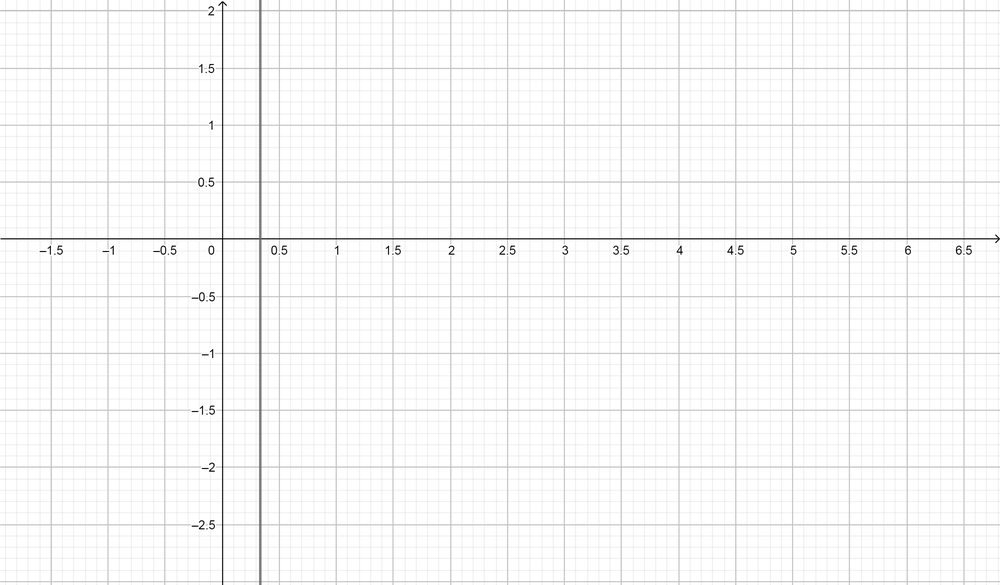
$$
color{#4257b2}text{(d)} log(4x)=log(x+1)
$$

From the graph $(x=0.32)$

$$
text{color{#c34632}(a) $x=0.8$ (b) $x=2.15$
\ \
(c) $x=1.64$ (d) $x=0.32$}
$$

Solve the following expression.

$$
color{#4257b2} log_5(x-1)+log_5(x-2)-log_5(x+6)=0
$$

Use standard form as follows:

$$
because log_a(x)+log_a(y)=log_a(xcdot y)
$$

$$
therefore log_5(x-1)+log_5(x-2)-log_5(x+6)=0 log_5[(x-1)(x-2)]-log_5(x+6)=0
$$

$$
log_5(x^2-3x+2)-log_5(x+6)=0
$$

Use standard form as follows:

$$
because log_a(x)-log_a(y)=log_aleft(dfrac{x}{y}right)
$$

$$
therefore log_5(x^2-3x+2)-log_5(x+6)=0 log_5left(dfrac{x^2-3x+2}{x+6}right)=0
$$

Use exponential standard form as follows:

$$
because log_a(x)=b therefore x=a^b
$$

$$
because log_5left(dfrac{x^2-3x+2}{x+6}right)=0
$$

$$
therefore dfrac{x^2-3x+2}{x+6}=5^0=1
$$

Isolate the variables $x$ in the left side as follows:

$$
x^2-3x+2=x+6 x^2+(-3x-x)+(2-6)=0
$$

$$
x^2-4x-4=0
$$

Use completing square to solve the equation as follows:

$$
x^2-4x+4=4+4 (x-2)^2=8
$$

Use square root property as follows:

$$
sqrt{(x-2)^2}=sqrt{8} x-2=pmsqrt{8}
$$

$$
x=2pmsqrt{8}
$$

$$
text{color{#c34632}$x=2pmsqrt{8}$}
$$

Explain why there are no solution for the following equations.

$$
color{#4257b2}log_3(-8)=x log_{-3}(9)=x
$$

When solving the logarithmic equation, be sure to check for inadmissible solution. A solution is inadmissible, if its substitution in the original equation result in a undefined value.

Remember that, the argument and the base of logarithm must be $text{color{#4257b2}positive.}$

$$
text{color{#c34632} When solving the logarithmic equation, be sure to check for inadmissible solution. A solution is inadmissible, if its substitution in the original equation result in a undefined value.
\ \
Remember that, the argument and the base of logarithm must be color{#4257b2}positive.}
$$

$$
text{color{#4257b2}(a) Without solving the following equation, find the value of variables $x$.}
$$

$$
color{#4257b2} log(2x-5)-log(x-3)=5
$$

The value of the variable $x$ is very small value because when we use the exponent standard form to get the value of $x$ at the base of logarithm is $(10)$, you get a large value, so this value is exist and out of chart when you graph it.

$$
text{color{#4257b2}(b) Why these restriction exist?}
$$

The value of the variable $x$ is very small.

$$
text{color{Black}(a) The value of the variable $x$ is very small value because when we use the exponent standard form to get the value of $x$ at the base of logarithm is $(10)$, you get a large value, so this value exists and out of chart when you graph it.
\ \
(b) The value of the variable $x$ is very small.}
$$

$$
text{color{#4257b2}If $logleft(dfrac{x+y}{5}right)=dfrac{1}{2} [log(x)+log(y)]$, show that $x^2+y^2=23xy$}
$$

$$
logleft(dfrac{x+y}{5}right)=dfrac{1}{2} log(xcdot y)
$$

Multiply both of sides by value of $(2)$ as follows:

$$
2 logleft(dfrac{x+y}{5}right)=log(xcdot y) logleft(dfrac{x+y}{5}right)^2=log(xcdot y)
$$

Use standard form for the logarithmic equations as follows:

$$
because log_a(x)=log_a(y) therefore x=y
$$

$$
because logleft(dfrac{x+y}{5}right)^2=log(xcdot y) therefore left(dfrac{x+y}{5}right)^2=xcdot y
$$

$$
(x+y)^2=25xy x^2+2xy+y^2=25xy
$$

$$
x^2+y^2=25xy-2xy x^2+y^2=23xy
$$

$$
text{color{#c34632}$x^2+y^2=23xy$}
$$

We would like to solve the following expression

$$
color{#4257b2}dfrac{log(35-x^3)}{log(5-x)}=3
$$

Multiply both side with each other as follows:

$$
log(35-x^3)=3 log(5-x) log(35-x^3)=log(5-x)^3
$$

Use the following standard form:

$$
because log_a(x)=log_a(y) therefore x=y
$$

$$
because log(35-x^3)=log(5-x)^3 therefore (35-x^3)=(5-x)^3
$$

Use distributive property as follows:

$$
(35-x^3)=(5-x)(5-x)^2 (35-x^3)=(5-x)(25-10x+x^2)
$$

$$
(35-x^3)=5(25-10x+x^2)-x(25-10x+x^2)
$$

$$
(35-x^3)=125-50x+5x^2-25x+10x^2-x^3
$$

Rearrange the tiles to group like terms as follows:

$$
(x^3-x^3)+(5x^2+10x^2)+(-50x-25x)+(125-35)=0
$$

$$
15x^2-75x+90
$$

Divide both of sides by $(15)$ as follows:

$$
x^2-5x+6=0 (x-2)(x-3)=0
$$

Use zero property as follows:

$$
x-2=0, x=2 x-3=0, x=3
$$

$$
text{color{#c34632}$x=2 text{or} x=3$}
$$

Calculate the values of $(a, b)$ for the following expression.

$$
color{#4257b2}log_2(a)+log_2(b)=4
$$

According the following standard form:

$$
because log_a(x)+log_a(y)=log_a(xcdot y)
$$

$$
therefore log_2(a)+log_2(b)=4 log_2(acdot b) =4
$$

Use exponential standard form as follows:

$$
because log_a(x)=b therefore x=a^b
$$

$$
because log_2(acdot b) =4 ab=2^4=16
$$

$$
therefore a=dfrac{16}{b} b=dfrac{16}{a}
$$

$$
text{color{#c34632}$a=dfrac{16}{b} text{and} b=dfrac{16}{a}$}
$$

Since the left hand-sides of these equations are equal, we can equate the right-hand sides as well, to obtain one equation with one variable $x$, and solve for $x$. It yields:
$$
log_2(5x+4)=3+log_2(x-1).$$

While solving this equation note the properties of the logarithm
$$
begin{align*}
log_ax&=biff x=a^bquadquad(1)\
log_adfrac{x}{y}&=log_ax-log_ayquadquad(2)end{align*}$$
Afterward, when we obtain the values of $x$ we can substitute that value into any given equation to obtain the value of $y$.

Substituting $log_2(x-1)$ throughout the equation and solving for $x$, we obtain:
$$
begin{align*}
log_2(5x+4)-log_2(x-1)&=3\
log_2dfrac{5x+4}{x-1}&=3&&text{[Property (2)]}\
dfrac{5x+4}{x-1}&=2^3&&text{[Property (1)]}\
dfrac{5x+4}{x-1}&=8\
dfrac{5x+4}{x-1}-8&=0&&text{[Substitute $8$ throughout]}\
dfrac{5x+4}{x-1}-dfrac{8(x-1)}{x-1}&=0&&text{[Expand $8$]}\
dfrac{5x+4-8(x-1)}{x-1}&=0\
dfrac{5x+4-8x+8}{x-1}&=0\
dfrac{-3x+12}{x-1}&=0&&left[frac{a}{b}=0iff a=0, bnot=0right]\
-3x+12&=0&&text{[Subtract $12$ throughout]}\
-3x&=-12&&text{[Divide by $-3$ throughout]}\
x&=4.
end{align*}$$

Substituting the value $x=4$ into any of the given equations, we obtain the value of $y$. We can choose first equation and obtain
$$
y=log_2(5cdot4+4)=log_224approx 4.59$$
Hence, the solution to this system of equations is
$$
begin{align*}
x&=4\
y&=4.59.
end{align*}$$

$x=4$, $y=4.59$

We would like to solve the following expressions.

$$
color{#4257b2}text{a)} log_5(log_3(x))=0
$$

Use standard form as follows:

$$
because log_a(x)=b therefore x=a^b
$$

$$
therefore log_5(log_3(x))=0 5^0=1=log_3(X)
$$

$$
x=3^1 x=3
$$

$$
color{#4257b2}text{b)} log_2(log_4(x))=1
$$

Use standard form as follows:

$$
because log_a(x)=b therefore x=a^b
$$

$$
therefore log_2(log_4(x))=1 2^1=2=log_4(X)
$$

$$
x=4^2 x=16
$$

$$
text{color{#c34632}(a) $x=3$ (b) $x=16$}
$$

If $left(dfrac{1}{2}right)^{x+y}=16, log_{x-y}(8)=-3$. Calculate the value of $x, y$.

$$
text{color{#4257b2}For $left(dfrac{1}{2}right)^{x+y}=16$}
$$

Write the $(16)$ as a power of $left(dfrac{1}{2}right)$ as follows:

$$
left(dfrac{1}{2}right)^{x+y}=left(dfrac{1}{2}right)^{-4}
$$

Since the base of exponential equals, so the power is equal as follows:

$$
x+y=-4 text{Equ. (1)}
$$

$$
text{color{#4257b2}For $log_{x-y}(8)=-3$}
$$

Use standard exponential form as follows:

$$
because log_a(x)=b therefore x=a^b
$$

$$
because log_{x-y}(8)=-3 therefore (x-y)^{-3}=8
$$

Write the $(8)$ as a power of $(-3)$ as follows:

$$
(x-y)^{-3}=left(dfrac{1}{2}right)^{-3}
$$

Since the power of exponential is equals, so the base is equasl as follows:

$$
x-y=dfrac{1}{2} text{Equ. (2)}
$$

Solve Equ $(1, 2)$ as follows:

$$
x+y=-4 x-y=dfrac{1}{2}
$$

Use elimination property as follows:

$$
(x+x)+(y-y)=left(-4+dfrac{1}{2}right) 2x=-dfrac{7}{2}
$$

Divide both of sides by value of $(2)$ as follows:

$$
x=-dfrac{7}{4}
$$

Substitute the value of $left(x=-dfrac{7}{4}right)$ in the first equation, to get the value of $y$ as follows:

$$
x+y=-4 -dfrac{7}{4}+y=-4 y=-4+dfrac{7}{4}
$$

$$
y=dfrac{-16+7}{4} y=-dfrac{9}{4}
$$

$$
text{color{#c34632}$x=-dfrac{7}{4} text{and} y=-dfrac{9}{4}$}
$$