Express in logarithmic form for the following expression.

$$
color{#4257b2}text{(a)} 4^2=16
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
=log_4(16)=2
$$

$$
color{#4257b2}text{(b)} 4^3=81
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
=log_4(81)=3
$$

$$
color{#4257b2}text{(c)} 8^0=1
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
=log_8(1)=0
$$

$$
color{#4257b2}text{(d)} 6^{-2}=dfrac{1}{36}
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
=log_6left(dfrac{1}{36}right)=-2
$$

$$
color{#4257b2}text{(e)} left(dfrac{1}{3}right)^3=dfrac{1}{27}
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
=log_{tfrac{1}{3}}left(dfrac{1}{27}right)=3
$$

$$
color{#4257b2}text{(f)} 8^{left(tfrac{1}{3}right)}=2
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
=log_8(2)dfrac{1}{3}
$$

$$
text{color{#c34632}(a) $=log_4(16)=2$ (b) $=log_4(81)=3$
\ \
(c) $=log_8(1)=0$ (d) $=log_6left(dfrac{1}{36}right)=-2$
\ \
(e) $=log_{tfrac{1}{3}}left(dfrac{1}{27}right)=3$ (f) $=log_8(2)=dfrac{1}{3}$}
$$

Express in exponential form for the following expression.

$$
color{#4257b2}text{(a)} log_2(8)=3
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
2^3=8
$$

$$
color{#4257b2}text{(b)} log_5left(dfrac{1}{25}right)=-2
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
5^{-2}=dfrac{1}{25}
$$

$$
color{#4257b2}text{(c)} log_3(81)=4
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
3^4=81
$$

$$
color{#4257b2}text{(d)} log_{tfrac{1}{6}}(216)=-3
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
left(dfrac{1}{6}right)^{-3}=216
$$

$$
color{#4257b2}text{(e)} log_6(sqrt{6})=dfrac{1}{2}
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
6^{left(tfrac{1}{2}right)}=sqrt{6}
$$

$$
color{#4257b2}text{(f)} log_{10}(1)=0
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
10^0=1
$$

$$
text{color{#c34632}(a) $2^3=8$ (b) $5^{-2}=dfrac{1}{25}$
\ \
(c) $3^4=81$ (d) $left(dfrac{1}{6}right)^{-3}=216$
\ \
(e) $=6^{left(tfrac{1}{2}right)}=sqrt{6}$ (f) $=10^0=1$}
$$

Evaluate the following expression.

$$
color{#4257b2}text{(a)} log_5(5)
$$

According the general form $log_a(a)=1$

$$
log_5(5)=1
$$

$$
color{#4257b2}text{(b)} log_7(1)
$$

To evaluate the expression, write it in the exponential form to which $(7)$ must be raised to get $(1)$ as follows:

$$
7^x=1
$$

Rewrite $(1)$ as a power of $(7)$ as follows:

$$
7^x=7^0 x=0
$$

$$
log_7(1)=0
$$

$$
color{#4257b2}text{(c)} log_2left(dfrac{1}{4}right)
$$

To evaluate the expression, write it in the exponential form to which $(2)$ must be raised to get $left(dfrac{1}{4}right)$ as follows:

$$
2^x=dfrac{1}{4}
$$

Rewrite $left(dfrac{1}{4}right)$ as a power of $(2)$ as follows:

$$
2^x=2^{-2} x=-2
$$

$$
log_2left(dfrac{1}{4}right)=-2
$$

$$
color{#4257b2}text{(d)} log_7(sqrt{7})
$$

To evaluate the expression, write it in the exponential form to which $(7)$ must be raised to get $(sqrt{7})$ as follows:

$$
7^x=sqrt{7}
$$

Rewrite $(sqrt{7})$ as a power of $(7)$ as follows:

$$
7^x=7^{tfrac{1}{2}} x=dfrac{1}{2}
$$

$$
log_7(sqrt{7})=dfrac{1}{2}
$$

$$
color{#4257b2}text{(e)} log_{tfrac{2}{3}}left(dfrac{8}{27}right)
$$

To evaluate the expression, write it in the exponential form to which $left(dfrac{2}{3}right)$ must be raised to get $left(dfrac{8}{27}right)$ as follows:

$$
left(dfrac{2}{3}right)^x=dfrac{8}{27}
$$

Rewrite $left(dfrac{8}{27}right)$ as a power of $left(dfrac{2}{3}right)$ as follows:

$$
left(dfrac{2}{3}right)^x=left(dfrac{2}{3}right)^3 x=3
$$

$$
log_{tfrac{2}{3}}left(dfrac{8}{27}right)=3
$$

$$
color{#4257b2}text{(f)} log_2(sqrt[3]{2})
$$

To evaluate the expression, write it in the exponential form to which $(2)$ must be raised to get $(sqrt[3]{2})$ as follows:

$$
2^x=sqrt[3]{2}
$$

Rewrite $(sqrt[3]{2})$ as a power of $(2)$ as follows:

$$
2^x=2^{left(tfrac{1}{3}right)} x=dfrac{1}{3}
$$

$$
log_2(sqrt[3]{2})=dfrac{1}{3}
$$

$$
text{color{#c34632}(a) $log_5(5)=1$ (b) $log_7(1)=0$
\ \
(c) $log_2left(dfrac{1}{4}right)=-2$ (d) $log_7(sqrt{7})=dfrac{1}{2}$
\ \
(e) $log_{tfrac{2}{3}}left(dfrac{8}{27}right)=3$ (f) $log_2(sqrt[3]{2})=dfrac{1}{3}$}
$$

Solve for $x$, for the following expression.

$$
color{#4257b2}text{(a)} logleft(dfrac{1}{10}right)=x
$$

Note that $color{#4257b2}log (10)=log_{10} (10)$, so you can use this rule to rewrite the expression as follows:

$$
log_{10}left(dfrac{1}{10}right)=x
$$

Use the exponential form to write the expression as follows:

$$
log_a (x)=y a^x=y
$$

$$
log_{10}left(dfrac{1}{10}right)=x 10^x=dfrac{1}{10}
$$

Rewrite the $dfrac{1}{10}$ as a powered of $10$ as follows:

$$
10^x=10^-1 x=-1
$$

$$
color{#4257b2}text{(b)} log(1)=x
$$

Note that $color{#4257b2}log (a)=log_{10} (a)$, so you can use this rule to rewrite the expression as follows:

$$
log_{10}(1)=x
$$

Use the exponential form to write the expression as follows:

$$
log_a (x)=y a^x=y
$$

$$
log_{10}(1)=x 10^x=1
$$

Rewrite the $1$ as a powered of $10$ as follows:

$$
10^x=10^0 x=0
$$

$$
color{#4257b2}text{(c)} log(1,000,000)=x
$$

Note that $color{#4257b2}log (a)=log_{10} (a)$, so you can use this rule to rewrite the expression as follows:

$$
log_{10} (1,000,000)=x
$$

Use the exponential form to write the expression as follows:

$$
log_a (x)=y a^x=y
$$

$$
log_{10}(1,000,000)=x 10^x=1,000,000
$$

Rewrite the $1,000,000$ as a powered of $10$ as follows:

$$
10^x=10^6 x=6
$$

$$
color{#4257b2}text{(d)} log(25)=x
$$

Note that $color{#4257b2}log (a)=log_{10} (a)$, so you can use this rule to rewrite the expression as follows:

$$
log_{10}(25)=x
$$

Use the exponential form to write the expression as follows:

$$
log_a (x)=y a^x=y
$$

$$
log_{10}(25)=x 10^x=25
$$

Rewrite the $25$ as a powered of $10$ as follows:

$$
10^x=10^{1.4} text{Approximately} x=1.4
$$

$$
color{#4257b2}text{(e)} log(x)=0.25
$$

Note that $color{#4257b2}log (a)=log_{10} (a)$, so you can use this rule to rewrite the expression as follows:

$$
log_{10} (x)=0.25
$$

Use the exponential form to write the expression as follows:

$$
log_a (x)=y a^x=y
$$

$$
log_{10}(x)=0.25 10^x=0.25
$$

Rewrite the $1,000,000$ as a powered of $10$ as follows:

$$
10^x=10^-{0.602} x=-0.602
$$

$$
color{#4257b2}text{(f)} log(x)=-2
$$

Note that $color{#4257b2}log (a)=log_{10} (a)$, so you can use this rule to rewrite the expression as follows:

$$
log_{10}(x)=-2
$$

Use the exponential form to write the expression as follows:

$$
log_a (x)=y a^x=y
$$

$$
log_{10}(x)=-2 10^x=-2
$$

Rewrite the $25$ as a powered of $10$ as follows:

$$
10^x=10^{0.3} text{Approximately} x=0.3
$$

$$
text{color{#c34632}(a) $x=-1$ (b) $x=0$
\ \
(c) $x=6$ (d) $x=1.4$
\ \
(e) $x=-0.602$ (f) $x=0.3$}
$$

Evaluate the following expression.

$$
color{#4257b2}text{(a)} log_6left(sqrt{6}right)
$$

To evaluate the expression, write it in the exponential form to which $(6)$ must be raised to get $(sqrt{6})$ as follows:

$$
6^x=sqrt{6}
$$

Rewrite $(sqrt{6})$ as a power of $(6)$ as follows:

$$
6^x=6^{tfrac{1}{2}} x=dfrac{1}{2}
$$

$$
log_6(sqrt{6})=dfrac{1}{2}
$$

$$
color{#4257b2}text{(b)} log_5(125)-log_{5}(25)
$$

Now, we can use the logarithmic property as follows:

$$
log_a(x)-log_a(y) log_aleft(dfrac{x}{y}right)
$$

$$
log_5left(dfrac{125}{25}right) log_5(5)
$$

According the general form $log_a(a)=1$

$$
log_5(5)=1
$$

$$
color{#4257b2}text{(c)} log_3(81)-log_{4}(64)
$$

Evaluate the expression as two parts as follows:

$$
log_3(81)
$$

To evaluate the expression, write it in the exponential form to which $(3)$ must be raised to get $(81)$ as follows:

$$
3^x=81
$$

Rewrite $(81)$ as a power of $(3)$ as follows:

$$
3^x=3^4 x=4
$$

$$
log_4(64)
$$

To evaluate the expression, write it in the exponential form to which $(4)$ must be raised to get $(64)$ as follows:

$$
4^x=64
$$

Rewrite $(64)$ as a power of $(4)$ as follows:

$$
4^x=4^3 x=3
$$

$$
log_3(81)-log_{4}(64)=4-3=1 log_3(81)-log_{4}(64)=1
$$

$$
color{#4257b2}text{(d)} log_2left(dfrac{1}{4}right)-log_3(1)
$$

Evaluate the expression as two parts as follows:

$$
log_2left(dfrac{1}{4}right)
$$

To evaluate the expression, write it in the exponential form to which $(2)$ must be raised to get $left(dfrac{1}{4}right)$ as follows:

$$
2^x=dfrac{1}{4}
$$

Rewrite $left(dfrac{1}{4}right)$ as a power of $(2)$ as follows:

$$
2^x=2^-2 x=-2
$$

$$
log_3(1)
$$

To evaluate the expression, write it in the exponential form to which $(3)$ must be raised to get $(1)$ as follows:

$$
3^x=1
$$

Rewrite $(1)$ as a power of $(3)$ as follows:

$$
3^x=3^0 x=0
$$

$$
log_2left(dfrac{1}{4}right)-log_3(1)=-2-0=-2 log_2left(dfrac{1}{4}right)-log_3(1)=-2
$$

$$
color{#4257b2}text{(e)} log_5(sqrt[3]{5})
$$

To evaluate the expression, write it in the exponential form to which $(5)$ must be raised to get $(sqrt[3]{5})$ as follows:

$$
5^x=sqrt[3]{5}
$$

Rewrite $(sqrt[3]{5})$ as a power of $(5)$ as follows:

$$
5^x=5^{left(tfrac{1}{3}right)} x=dfrac{1}{3}
$$

$$
log_5(sqrt[3]{5})=dfrac{1}{3}
$$

$$
color{#4257b2}text{(f)} log_5(sqrt{27})
$$

To evaluate the expression, write it in the exponential form to which $(3)$ must be raised to get $(sqrt{27})$ as follows:

$$
3^x=sqrt{27}
$$

Rewrite $(sqrt{27})$ as a power of $(3)$ as follows:

$$
3^x=3^{left(tfrac{3}{2}right)} x=dfrac{3}{2}
$$

$$
log_3(sqrt{27})=dfrac{3}{2}
$$

$$
text{color{#c34632}
(a) $dfrac{1}{2}$ (b) $1$ (c) $1$
\ \
(d) $-2$ (e) $dfrac{1}{3}$ (f) $dfrac{2}{3}$}
$$

Solve the value of $x$ for the following expression.

$$
color{#4257b2}text{(a)} log_5(x)=3
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
5^3=x x=125
$$

$$
color{#4257b2}text{(b)} log_x(27)=3
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
x^3=27
$$

Rewrite $(27)$ as a power of $(3)$ as follows:

$$
x^3=3^3 x=3
$$

$$
color{#4257b2}text{(c)} log_4left(dfrac{1}{64}right)=x
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
4^x=dfrac{1}{64}
$$

Rewrite $left(dfrac{1}{64}right)$ as a power of $(4)$ as follows:

$$
4^x=4^{-3} x=-3
$$

$$
color{#4257b2}text{(d)} log_{tfrac{1}{4}}(x)=-2
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
left(dfrac{1}{4}right)^{-2}=x x=left(dfrac{1}{left(tfrac{1}{4}right)^2}right)
$$

$$
left(dfrac{1}{left(tfrac{1}{16}right)}right)=x x=16
$$

$$
color{#4257b2}text{(e)} log_5(x)=dfrac{1}{2}
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
5^{left(tfrac{1}{2}right)}=x x=sqrt{5}
$$

$$
color{#4257b2}text{(f)} log_4(x)=1.5
$$

Standard form to write in logarithmic form is

$$
y=a^x y=log_a(x)
$$

$$
4^{1.5}=x x=8
$$

$$
text{color{#c34632}(a) $x=125$ (b) $x=3$
\ \
(c) $x=-3$ (d) $x=16$
\ \
(e) $x=sqrt{5}$ (f) $x=8$}
$$

Graph the function of $(fx)=3^x$, then use the graph to estimate the following logarithmic.

Estimate the following expression from the graph.

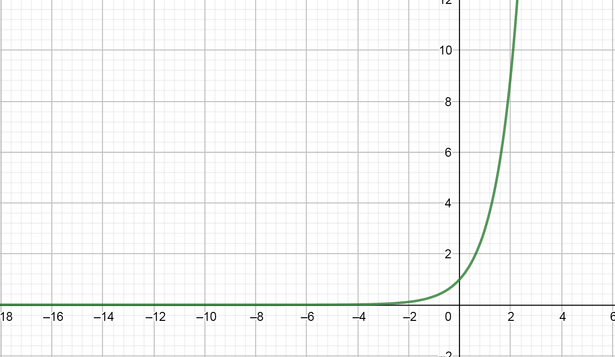
$$
color{#4257b2}text{(a)} log_3(17)
$$

From the graph at point $17$ $log_3(17)=2.5$

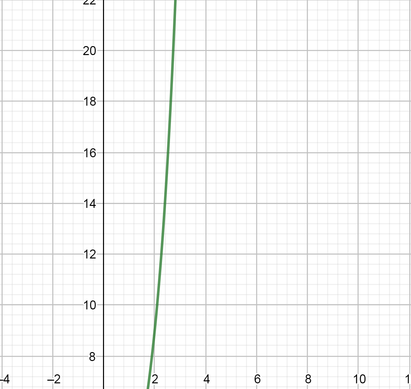
$$
color{#4257b2}text{(b)} log_3(36)
$$

From the graph at point $36$ $log_3(36)=3.22$

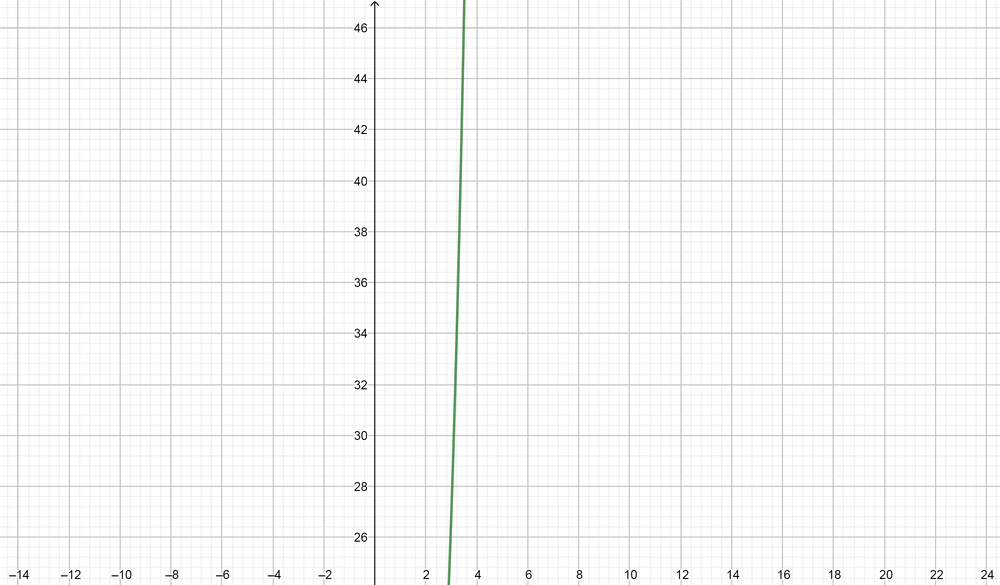
$$
color{#4257b2}text{(c)} log_3(112)
$$

From the graph at point $112$ $log_3(112)=4.25$

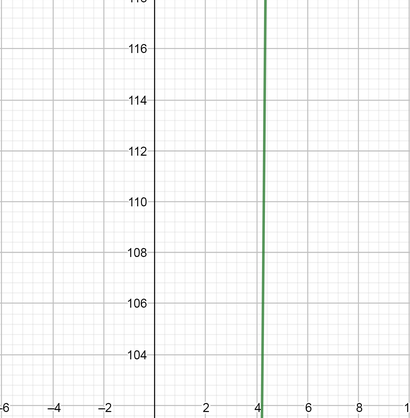
$$
color{#4257b2}text{(d)} log_3(143)
$$

From the graph at point $143$ $log_3(143)=4.45$

{$text{color{#c34632}
(a) $2.6$ (b) $3.22$ (c) $4.25$ (d) $4.45$}$

Estimate the value for the following logarithm.

$$
color{#4257b2}text{(a)} log_4(32)
$$

To evaluate the expression, write it in the exponential form to which $(4)$ must be raised to get $(32)$ as follows:

$$
4^x=32
$$

The exponent must be between $4^2=16, 4^3=64$

$$
4^x=4^{2.5} x=2.5
$$

$$
log_4(32)=2.5
$$

$$
color{#4257b2}text{(b)} log_6(115)
$$

To evaluate the expression, write it in the exponential form to which $(6)$ must be raised to get $(115)$ as follows:

$$
6^x=115
$$

The exponent must be between $6^2=36, 6^3=216$

$$
6^x=4^{2.6485} x=2.6485
$$

$$
log_6(115)=2.6485
$$

$$
color{#4257b2}text{(c)} log_3(212)
$$

To evaluate the expression, write it in the exponential form to which $(3)$ must be raised to get $(212)$ as follows:

$$
3^x=212
$$

The exponent must be between $3^4=81, 3^5=243$

$$
3^x=3^{4.876} x=4.876
$$

$$
log_3(212)=4.876
$$

$$
color{#4257b2}text{(d)} log_11(896)
$$

To evaluate the expression, write it in the exponential form to which $(11)$ must be raised to get $(896)$ as follows:

$$
11^x=896
$$

The exponent must be between $11^2=121, 11^3=1331$

$$
11^x=11^{2.835} x=2.835
$$

$$
log_{11}(896)=2.835
$$

$$
text{color{#c34632}
(a) $2.5$ (b) $2.6485$
\ \
(c) $4.876$ (d) $2.835$}
$$

Evaluate the following expression.

$$
color{#4257b2}text{(a)} log_3(3)^5
$$

According the general form $log_a(a)^x=x$ $therefore log_3(3)^5=5$

$$
color{#4257b2}text{(b)} 5^{(log_5(25))}
$$

According the general form $a^{(log_a(x))}=x$ $therefore 5^{(log_5(25))}=25$

$$
color{#4257b2}text{(c)} 4^{left(log_4left(tfrac{1}{16}right)right)}
$$

According the general form $a^{(log_a(x))}=x$ $therefore 4^{(log_4left(tfrac{1}{16}right)}=dfrac{1}{16}$

$$
color{#4257b2}text{(d)} log_m(m)^n
$$

According the general form $log_a(a)^x=x$ $therefore log_m(m)^n=n$

$$
color{#4257b2}text{(e)} a^{(log_a(b))}
$$

According the general form $a^{(log_a(x))}=x$ $therefore a^{(log_a(b))}=b$

$$
color{#4257b2}text{(f)} log_{tfrac{1}{10}}(1)
$$

To evaluate the expression, write it in the exponential form to

which $left(dfrac{1}{10}right)$ must be raised to get $(1)$ as follows:

$$
left(dfrac{1}{10}right)^x=1
$$

Rewrite $(1)$ as a power of $left(dfrac{1}{10}right)$ as follows:

$$
left(dfrac{1}{10}right)^x=left(dfrac{1}{10}right)^0 x=0
$$

$$
log_{tfrac{1}{10}}(1)=0
$$

$$
text{color{#c34632}
(a) $5$ (b) $25$ (c) $dfrac{1}{16}$
\ \
(d) $n$ (e) $b$ (f) $0$}
$$

Evaluate the following expression.

$$
color{#4257b2}text{(a)} log_2(16)^{left(tfrac{1}{3}right)}
$$

According the general form $log_a(a)^x=x log_a(a)$

$$
left(dfrac{1}{3}right) log_2(16)
$$

For $log_2(16)$ can be simplified as follows:

To evaluate the expression, write it in the exponential form to which $(2)$ must be raised to get $(16)$ as follows:

$$
2^x=16
$$

Rewrite $(16)$ as a power of $(2)$ as follows:

$$
2^x=2^4 x=4
$$

$$
log_2(16)=4
$$

$$
left(dfrac{1}{3}right) log_2(16)=dfrac{1}{3}cdot 4=dfrac{4}{3}
$$

Large{$text{color{#c34632} $dfrac{4}{3}$}$

How long will it take for there to be $2000$ spores? If increasing by a factor of $10$ every week and has an initial $40$ spores.

We make a general form can be used to get the number of spores at any time as follows:

$$
a_n=40+(10 n) text{Where}:
$$

$n=$ Time, week $a_n=$ Total number of spores.

$$
2000=40+(10n) 10n=2000-40
$$

$$
10n=1960
$$

Divide both of sides by $10$ as follows:

$$
n=dfrac{1960}{10} n=196text{ Weeks}
$$

The time needed to get total spores is $196$ weeks

$$
text{color{#c34632}$196$ weeks}
$$

The formula to calculate the remaining mass is $color{#4257b2}M(t)=Pleft(dfrac{1}{2}right)^{frac{t}{h}}$, where $color{#4257b2}h$ is half life and $color{#4257b2}P$ is initial mass. The half life of radium is $1620$ year.

$$
text{color{#4257b2}(a) If a laboratory hav a $(5)$ gram of radium, how much will there be in $(150)$ year?}
$$

$$
M(t)=Pleft(dfrac{1}{2}right)^{tfrac{t}{h}}
$$

$$
M(t)=5left(dfrac{1}{2}right)^{tfrac{150}{1620}}
$$

$$
M(t)=5left(dfrac{1}{2}right)^{0.09259}
$$

$$
M(t)=5 cdot 0.9378
$$

$$
M(t)=4.6891 text{gm}
$$

$$
text{color{#4257b2}(b) How many years take until the laboratory has a $(4)$ gram of radium?}
$$

$$
M(t)=Pleft(dfrac{1}{2}right)^{tfrac{t}{h}}
$$

$$
4=5left(dfrac{1}{2}right)^{tfrac{t}{1620}}
$$

Divide both of side by $(5)$ as follows:

$$
dfrac{4}{5}=left(dfrac{1}{2}right)^{tfrac{t}{1620}}
$$

Use logarithmic property as follows:

$$
logleft(dfrac{4}{5}right)=logleft(dfrac{1}{2}right)^{tfrac{t}{1620}}
$$

Accordion logarithmic property as follows:

$$
log(a)^n=n log(a)
$$

$$
logleft(dfrac{4}{5}right)=dfrac{t}{1620} logleft(dfrac{1}{2}right)
$$

Divide both of side by $left[logleft(dfrac{1}{2}right)right]$ as follows:

$$
dfrac{logleft(dfrac{4}{5}right)}{logleft(dfrac{1}{2}right)}=dfrac{t}{1620} 0.32193=dfrac{t}{1620}
$$

Use cross multiply property as follows:

$$
t=1620 cdot 0.32193 t=521.52 text{years}
$$

$$
text{color{#c34632}(a) $4.6891$ gm. (b) $521.52$ years.}
$$

We need to decide which one of the two beaches has a steeper slope.

The slope can be represented by $s(d)=0.159+0.118log(d)$

Beach $A$ has a diameter for fine sand grain $0.0625$ mm

Beach $B$ has a diameter for coarse sand grain $1$ mm

Substitute the value of $d$ at the slope expression for each beach as follows:

$$
text{color{#4257b2}Beach A, $d=0.0625$ mm}
$$

$$
s(d)=0.159+0.118log(0.0625)
$$

$$
s(d)=0.159+(0.118cdot-1.204) d=0.159-0.14209
$$

$$
s(d)=0.016914 text{ mm}
$$

$$
text{color{#4257b2}Beach B, $d=1$ mm}
$$

$$
s(d)=0.159+0.118log(1)
$$

$$
s(d)=0.159+(0.118cdot0) d=0.159+0
$$

$$
s(d)=0.159 text{ mm}
$$

From the above calculation, the beach $B$ has a steeper slope.

$$
text{color{#c34632}The beach $B$ has a steeper slope.}
$$

If the speed of the wind in mile per hour represented by $s(d)=93log(d)+65$, where $d$, the distance that the tornado travel in miles, answer for the following question.

$$
text{color{#4257b2}(a) if the tornado travel distance of $50$ miles, determine the speed of wind.}
$$

Substitute the value of $d=50$ as follows:

$$
s(d)=93log(50)+65 s(d)=(93cdot1.69897)+65
$$

$$
s(d)=158+65 s(d)=223
$$

The speed of wind if the tornado travel $50$ miles will be $223$ miles per hour.

$$
text{color{#4257b2}(b) if the tornado travel with speed of $250$ miles per hour, determine the distance of tornado travel.}
$$

Substitute the value of $s(d)=250$ as follows:

$$
250=93log(d)+65 93log(d)=250-65
$$

$$
93log(d)=185 log(d)=dfrac{185}{93}
$$

$$
log(d)=1.98924
$$

According the general form $log(a)=log_{10}(a)$

$$
log_{10}(d)=1.98924
$$

According the general form $log_{a}(x)=y a^x=y$

$$
d=10^{1.98924} d=97.55 text{Miles}
$$

The tornado travel $97.55$ miles with speed of $250$ miles per hour.

$$
text{color{#c34632}
(a) $s(d)=223$ miles per hour
\ \
(b) $d=97.55$ miles}
$$

Determine the time $D$ in days for the following expression.

$color{#4257b2}log(D)=frac{3}{2}log(k)-0.7$ and the distance of the earth about $150,000,000$ Km from the sun.

$$
log(D)=dfrac{3}{2}log(150,000,000)-0.7
$$

$$
log(D)=(dfrac{3}{2}cdot 9.1760913)-0.7
$$

$$
log(D)=13.76414-0.7
$$

$$
log(D)=13.064137
$$

According the general form $log(a)=log_{10}(a)$

$$
log(D)=log_{10}(D)=13.064137
$$

$$
D=10^{13.064137} D=115914.3 text{Million days}
$$

$$
text{color{#c34632} $D=115914.3 text{Million days}$}
$$

Use Kepler equation in question $15$ to determine the time in days for the following distances from the sun.

$$
color{#4257b2}text{(a) Uranus} 2854 text{million Km.}
$$

Kepler equation represented as follows:

$$
log(D)=dfrac{3}{2}log(k)-0.7
$$

$$
log(D)=dfrac{3}{2}log(2854,000,000)-0.7
$$

$$
log(D)=left(dfrac{3}{2}cdot 9.455454right)-0.7
$$

$$
log(D)=14.183181-0.7
$$

$$
log(D)=13.4831809
$$

According the general form $log(a)=log_{10}(a)$

$$
log(D)=log_{10}(D)=13.4831809
$$

$$
D=10^{13.4831809} D=304215.23 text{Million days}
$$

.
$$
color{#4257b2}text{(b) Neptune} 4473 text{million Km.}
$$

Kepler equation represented as follows:

$$
log(D)=dfrac{3}{2}log(k)-0.7
$$

$$
log(D)=dfrac{3}{2}log(4473,000,000)-0.7
$$

$$
log(D)=left(dfrac{3}{2}cdot 9.6505988right)-0.7
$$

$$
log(D)=14.4758983-0.7
$$

$$
log(D)=13.7758935
$$

According the general form $log(a)=log_{10}(a)$

$$
log(D)=log_{10}(D)=13.7758935
$$

$$
D=10^{13.7758935} D=59688889.63 text{Million days}
$$

$$
text{color{#c34632}
(a) $D=304215.23 text{Million days}$
\ \
(b) $D=59688889.63 text{Million days}$}
$$

Answer for the following question, if the bacteria culture has an initial number is $100$ with a doubling period of $0.32$ hr

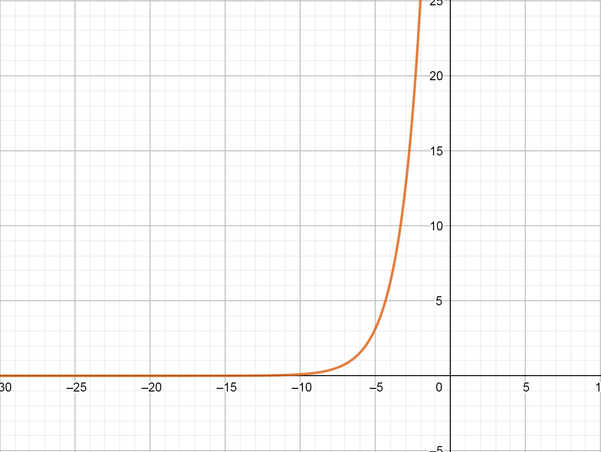
$$
text{color{#4257b2}(a) State the equation for the number of bacteria$y$, in hour $x$}
$$

We can use the following expression to determine the number of bacterial culture at any time:

$$
y=100 (2)^x
$$

$$
text{color{#4257b2}(b) Graph the equation}
$$

$$
text{color{#4257b2}(c) Graph the inverse.}
$$

$$
y=100log_2(x)
$$

$$
text{color{#4257b2}(d) State the equation for the inverse and explain, what does the equation represent?}
$$

$$
y=100cdot log_2(x)
$$

The equation represent the time at amount f culture bacterial.

$$
text{color{#4257b2}(e) Ho many hours will take to be there of $450$ bacterial cukture?}
$$

Use the equation represent the bacterial culture as follows:

$$
y=100cdot(2)^n text{Where:}
$$

$4n=$ total number of bacterial $n=$ Time, hour

$$
450=100(2)^n 2^n=dfrac{450}{100}
$$

$$
2^n=4.5
$$

Rewrite $4.5$ as a power of $2$ as follows:

$$
2^n=2^{2.17} n=2.17 text{Hour}
$$

The time needed for the bacterial to be $450$ is $2.17$ hour.

$$
text{color{#c34632}(a) $y=100 (2)^x$ (b) See graph. (c) See graph. \

(d) $y=100cdot log_2(x)$ (e) $2.17$ hours}
$$

Evaluate the following expression.

$$
color{#4257b2}text{(a)} log_5(5)
$$

According the general form $log_a(a)=1$

$$
log_5(5)=1
$$

$$
color{#4257b2}text{(b)} log_2(10)
$$

According the general form $log_a(b)=dfrac{log(b)}{log(a)}$

$$
log_2(10)=dfrac{log(10)}{log(2)} log_2(10)=dfrac{1}{0.3010}
$$

$$
log_2(10)=3.3222
$$

$$
color{#4257b2}text{(c)} log_5(45)
$$

According the general form $log_a(b)=dfrac{log(b)}{log(a)}$

$$
log_5(45)=dfrac{log(45)}{log(5)} log_5(45)=dfrac{1.653}{0.6989}
$$

$$
log_5(45)=2.365
$$

$$
color{#4257b2}text{(d)} log_8(92)
$$

According the general form $log_a(b)=dfrac{log(b)}{log(a)}$

$$
log_8(92)=dfrac{log(92)}{log(8)} log_8(92)=dfrac{19.64}{0.9031}
$$

$$
log_8(92)=2.175
$$

$$
color{#4257b2}text{(e)} log_4(0.5)
$$

According the general form $log_a(b)=dfrac{log(b)}{log(a)}$

$$
log_4(0.5)=dfrac{log(0.5)}{log(4)} log_4(0.5)=dfrac{-0.30103}{0.0.60206}
$$

$$
log_4(0.5)=-0.49995
$$

$$
color{#4257b2}text{(f)} log_7(325)
$$

According the general form $log_a(b)=dfrac{log(b)}{log(a)}$

$$
log_7(325)=dfrac{log(325)}{log(7)} log_7(325)=dfrac{2.51188}{0.84509}
$$

$$
log_7(325)=2.97222
$$

$$
text{color{#c34632}
(a) $1$ (b) $2.3222$ (c) $2.365$
\ \
(d) $2.175$ (e) $-0.49995$ (f) $2.97222$}
$$

Consider the expression of $log_5(a)$, then answer for the following question.

(a) For what values of $a$, will this expression yield positive number?

$$
color{#4257b2}a>1
$$

(b) For what values of $a$, will this expression yield negative number?

$$
color{#4257b2}0<a<1
$$

(c) For what values of $a$, will this expression be undefined?

$$
color{#4257b2}a<0
$$

$$
text{color{#c34632}(a) $a>1$ (b) $0<a<1$ (c) $a<0$}
$$

Simplify the following expression.

$$
color{#4257b2}text{(a)} 3^{log_3(27)}
$$

According the general form $a^{log_a(x)}=x$ $therefore 3^{log_3(27)}=27$

$$
color{#4257b2}text{(b)} 10^{log_{10}(100)}
$$

According the general form $a^{log_a(x)}=x$ $therefore 10^{log_{10}(100)}=100$

$$
color{#4257b2}text{(c)} 5^{log_5(8)}-3^{log_3(5)+log_3(7)}
$$

We determine each expression alone as follows:

For $5^{log_5(8)}$

According the general form $a^{log_a(x)}=x$

$$
5^{log_5(8)}=8
$$

According the general form $a^{log_a(x)} cdot a^{log_a(y)} =a^{[log_a(x)+log_a(y)]}$

$$
3^{log_3(5)+log_3(7)}=3^{log_3(5)} cdot 3^{log_3(7)}
$$

For $3^{log_3(5)}$

According the general form $a^{log_a(x)}=x$

$$
3^{log_3(5)}=5
$$

For $3^{log_3(7)}$

According the general form $a^{log_a(x)}=x$

$$
3^{log_3(7)}=7
$$

$$
3^{log_3(5)+log_3(7)}=3^{log_3(5)} cdot 3^{log_3(7)}
$$

$$
3^{log_3(5)+log_3(7)}=5cdot7=35
$$

$$
5^{log_5(8)}-3^{log_3(5)+log_3(7)}=8-35
$$

$$
5^{log_5(8)}-3^{log_3(5)+log_3(7)}=-27
$$

$$
text{color{#c34632}
(a) $27$ (b) $100$ (c) $-27$}
$$

State the inverse equation for the following expression.

$$
color{#4257b2}text{(a)} y=sqrt[3]{x}
$$

Substitute the value of $x=y$ as follows:

$$
x=sqrt[3]{y}=y^{tfrac{1}{3}}
$$

Isolate the $y$ variables on the left side and solve for it as follows::

$$
left(y^{tfrac{1}{3}}right)^3=x^3 y=x^3
$$

Substitute the value of $y=x$ as follows:

$$
f^{-1}(x)=x^3
$$

$$
color{#4257b2}text{(b)} y=3(2)^x
$$

According the general form of $y=a^x$ ha s an inverse function of $y=log_a(x)$

$$
f^{-1}(x)=3log_2(x)
$$

$$
color{#4257b2}text{(c)} y=(0.5)^{x+2}
$$

According the general form of $y=a^x$ ha s an inverse function of $y=log_a(x)$

$$
f^{-1}(x)=log_{0.5}(x+2)
$$

$$
color{#4257b2}text{(d)} y=3log_2(x-3)+2
$$

According the general form of $y=a^x$ ha s an inverse function of $y=log_a(x)$

$$
f^{-1}(x)=3(2)^{x-3}+2
$$

$$
text{color{#c34632}
(a) $f^{-1}(x)=x^3$ (b) $f^{-1}(x)=3log_2(x)$
\ \
(c) $f^{-1}(x)=log_{0.5}(x+2)$ (d) $f^{-1}(x)=3(2)^{x-3}+2$}
$$

Graph the following equation and its inverse, then state the domain, range, symptote equation for each one.

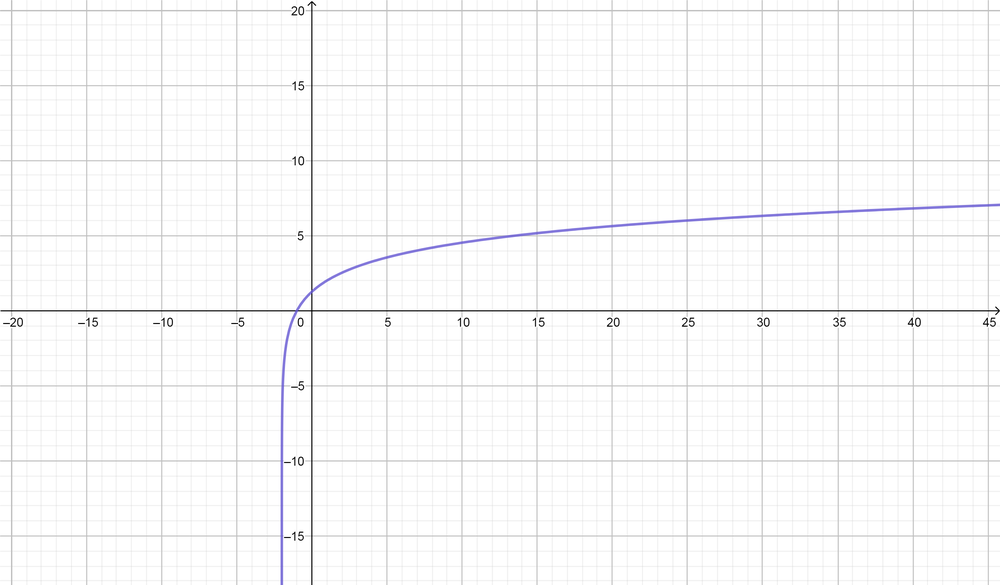
$$
color{#4257b2}text{(a)} y=3log(x+6)
$$

Domain $=(-6, infty),$ Range $=(-infty, infty),$ Symptote equation $(x=-6)$

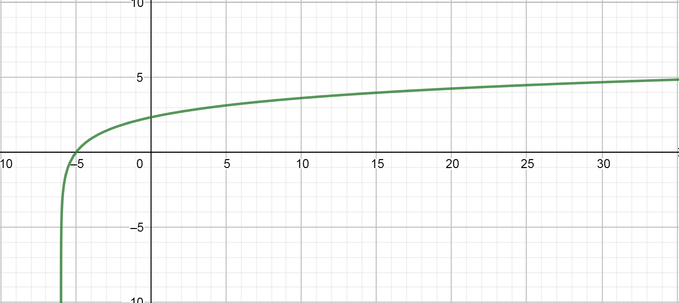
$$
color{#4257b2}text{(a) Inverse equation, } y=3log(x+6)
$$

Domain $=(-infty, infty),$ Range $=(0, infty),$ Symptote equation $(y=-6)$

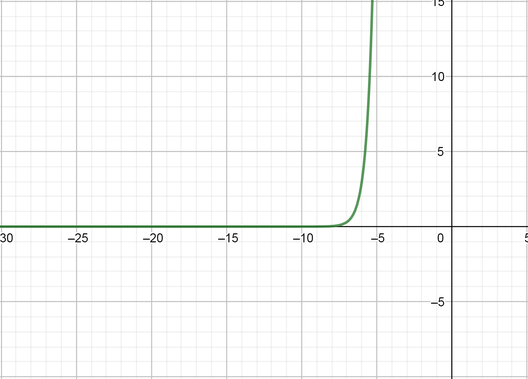
$$
color{#4257b2}text{(b)} y=-2log_5(3x)
$$

Domain $=(0, infty),$ Range $=(-infty, infty),$ Symptote equation $(x=0)$

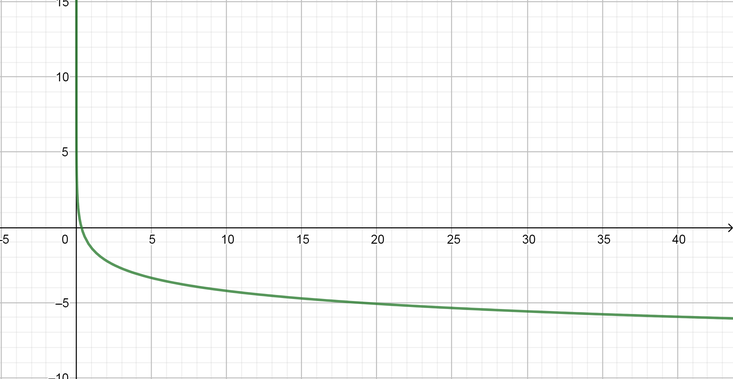
$$
color{#4257b2}text{(b) Inverse,} y=-2(5)^{3x}
$$

Domain $=(-infty, infty),$ Range $=(0, -infty),$ Symptote equation $(y=0)$

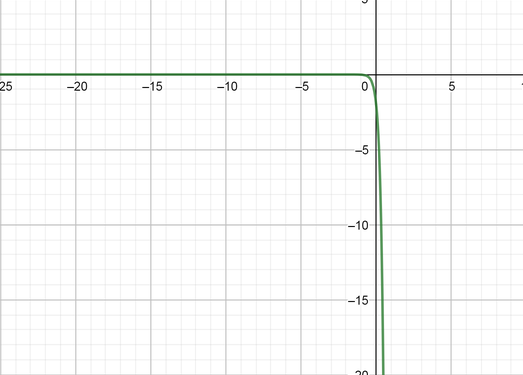
$$
color{#4257b2}text{(c)} y=2+3log(x)
$$

Domain $=(0, infty),$ Range $=(-infty, -infty),$ Symptote equation $(x=0)$

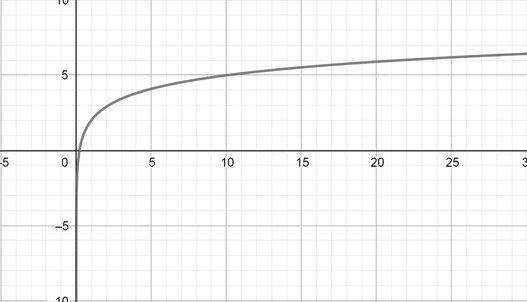
$$
color{#4257b2}text{(c) Inverse,} y=2+3(10)^x
$$

Domain $=(-infty, infty),$ Range $=(2, -infty),$ Symptote equation $(y=2)$

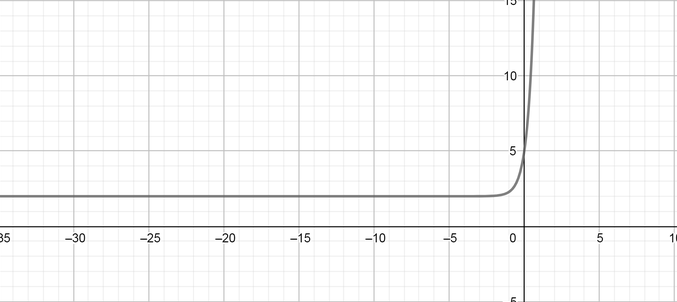
$$
color{#4257b2}text{(d)} y=20(8)^x
$$

Domain $=(-infty, infty),$ Range $=(0, infty),$ Symptote equation $(y=0)$

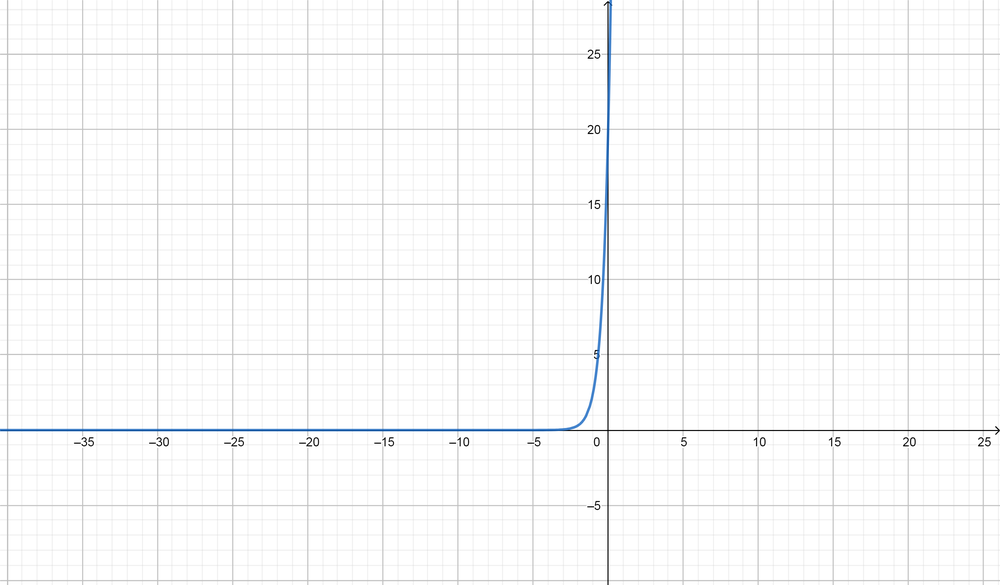
$$
color{#4257b2}text{(d) Inverse,} y=20log_8(x)
$$

Domain $=(0, infty),$ Range $=(-infty, infty),$ Symptote equation $(x=0)$

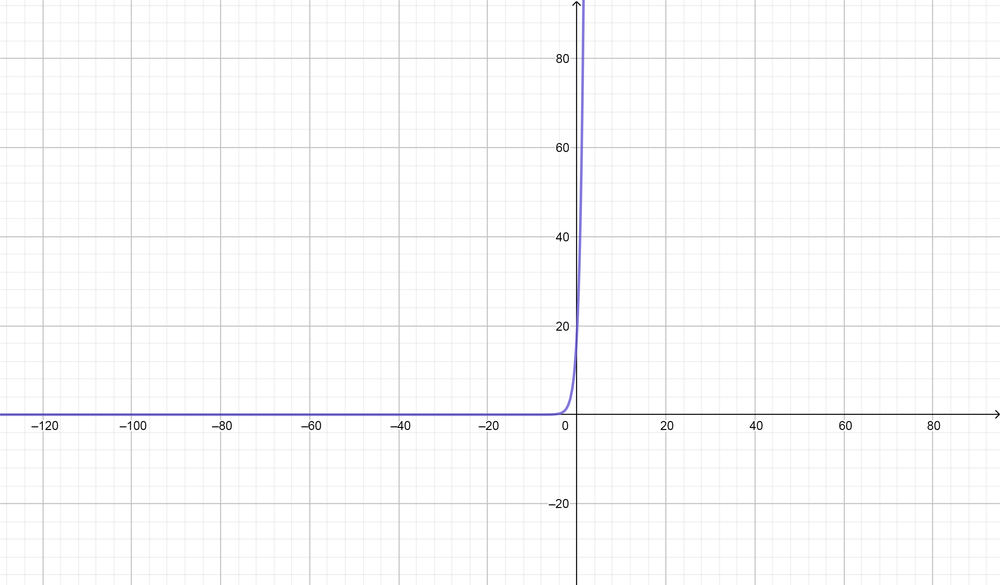
$$
color{#4257b2}text{(e)} y=2 (3)^{x+2}
$$

Domain $=(-infty, infty),$ Range $=(0, infty),$ Symptote equation $(y=0)$

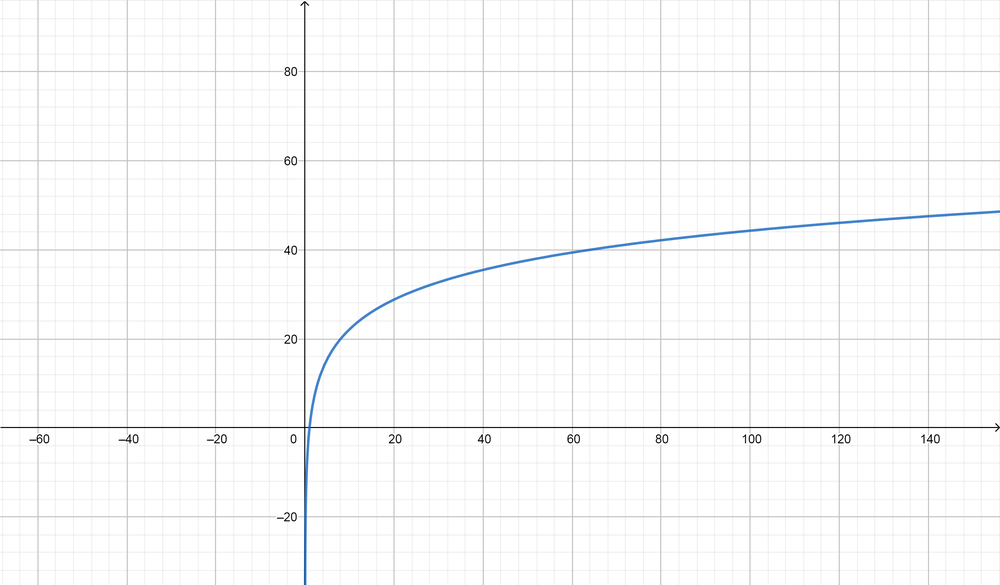
$$
color{#4257b2}text{(e) Inverse,} y=2log_3(x+2)
$$

Domain $=(-2, infty),$ Range $=(-infty, infty),$ Symptote equation $(x=-2)$

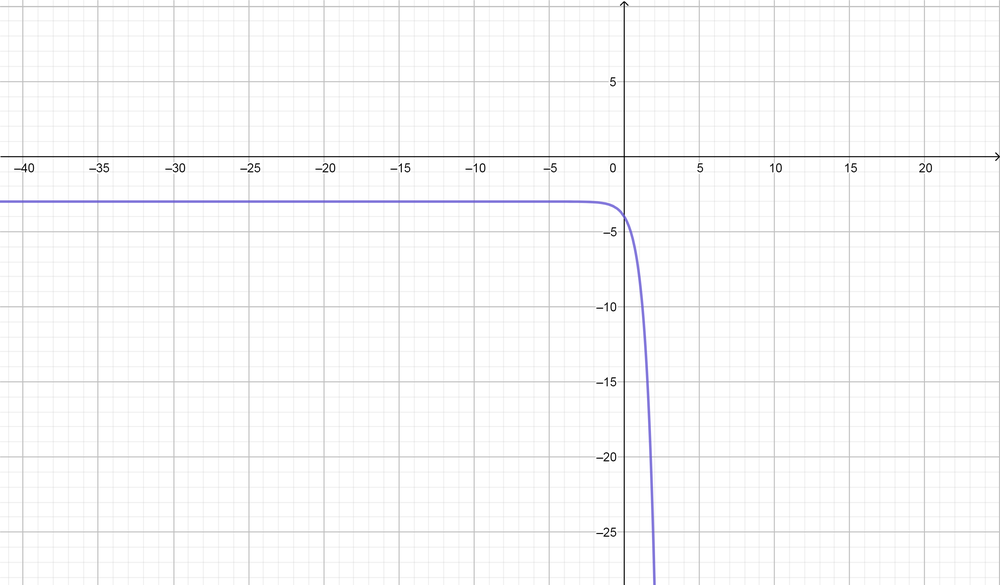
$$
color{#4257b2}text{(f)} y=-5^x-3
$$

Domain $=(-infty, infty),$ Range $=(-3, -infty),$ Symptote equation $(y=-3)$

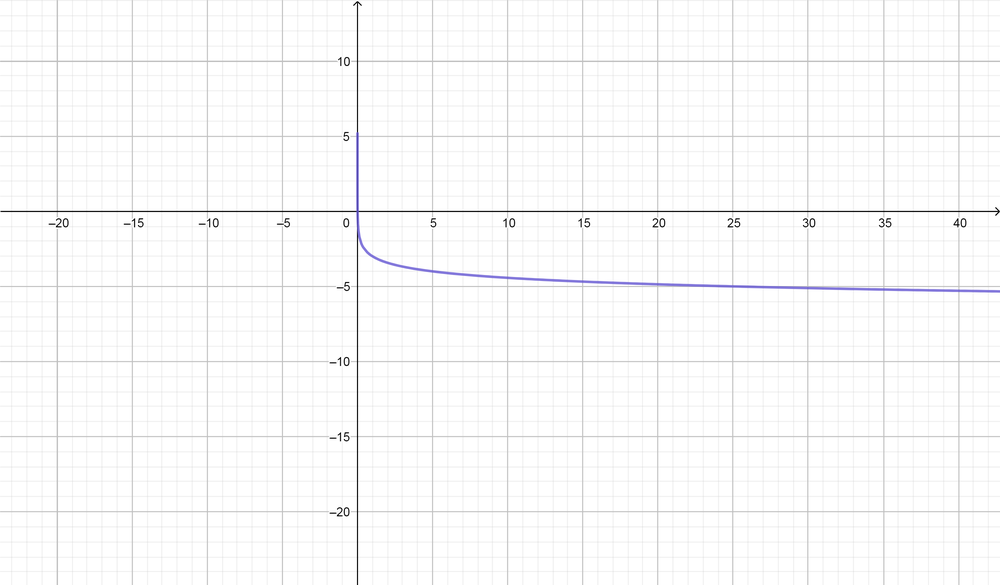
$$
color{#4257b2}text{(f) Inverse,} y=-log_5(x-3)
$$

Domain $=(0, infty),$ Range $=(-infty, infty),$ Symptote equation $(x=0)$

$$
text{color{#c34632}Large See graphs}
$$

How many integer values of $y$ for the function $y=log_{10}(x)$
where
$0<x-20$

$$
text{color{#4257b2}For the value of $x>0$ x=1}
$$

$$
y=log_{10}(x) y=log_{10}(1) y=0
$$

$$
text{color{#4257b2}For the value of $x<1000$ x=999}
$$

$$
y=log_{10}(x) y=log_{10}(999) y=2.99956
$$

The integer values of $y$ are $0<y<2.99956$

$$
text{color{#c34632}Large The integer values of $y$ are $0<y<2.99956$}
$$