Describe the transformation that applied to the $f(x)$ to graph $g(x)$.

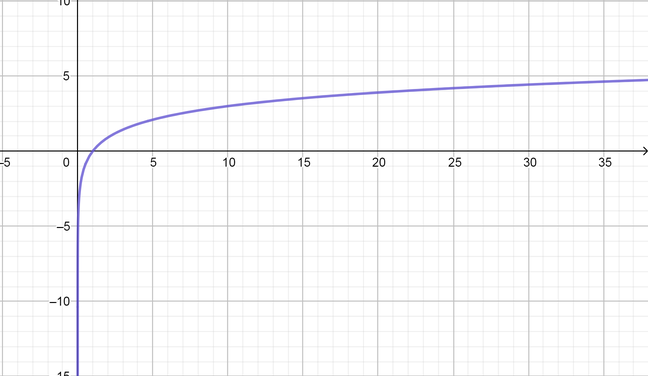
$$
color{#4257b2}text{(a)} g(x) =3log_{10} x
$$

The transformation applied is:

Vertical stretch factor is $a=3$

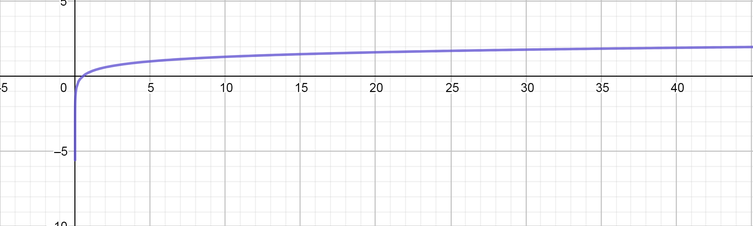
$$
color{#4257b2}text{(b)} g(x) =log_{10} 2x
$$

The transformation applied is:

Horizontal stretch factor is $k=2$

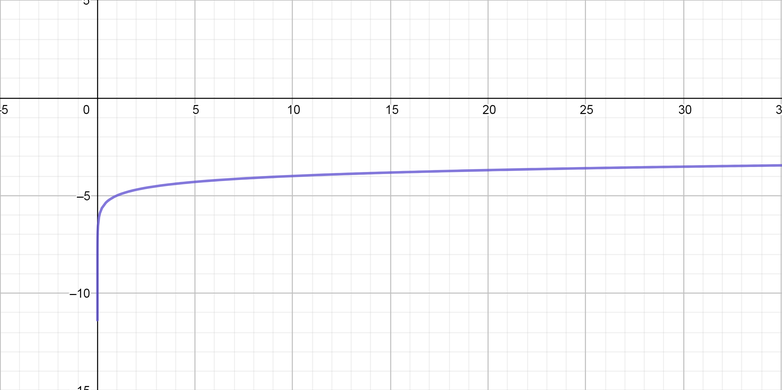
$$
color{#4257b2}text{(c)} g(x) =log_{10} x -5
$$

The transformation applied is:

Vertical translated factor is $c=-5$

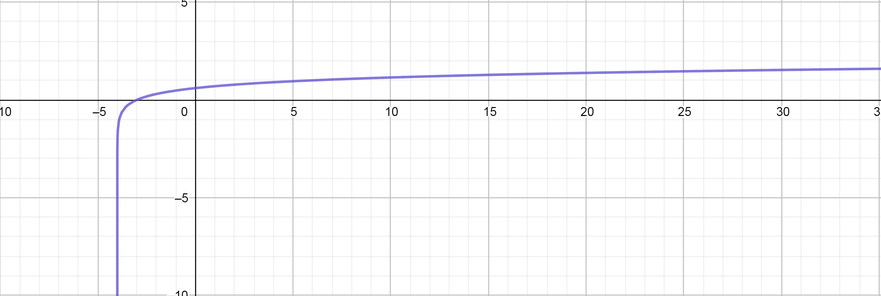
$$
color{#4257b2}text{(d)} g(x) =log_{10} (x+4)
$$

The transformation applied is:

Horizontal translated factor is $d=-4$

$$
text{color{#c34632}(a) Vertical stretch factor is $a=3$
\ \
(b) Horizontal stretch factor is $k=2$
\ \
(c) Vertical translated factor is $c=-5$
\ \
(d) Horizontal translated factor is $d=-4$}
$$

$$
text{color{#4257b2}(a) State the coordinate of the following points for each function in the question $1$.

$$left(dfrac{1}{10}, -1right), (1, 0), (10, 1)$$}
$$

$$
color{#4257b2}text{(I)} g(x)=3log_{10}x
$$

Multiply the coordinate of $y$ points by $3$ as follows $(x, y)rightarrow(x, 3y)$:

$$
left(dfrac{1}{10}, -1right)rightarrowleft(dfrac{1}{10}, -3right)
$$

$$
(1, 0)rightarrow(1, 0)
$$

$$
(10, 1)rightarrow(10, 3)
$$

$$
color{#4257b2}text{(II)} g(x)=log_{10}2x
$$

Multiply the coordinate of $x$ points by $2$ as follows $(x, y)rightarrow(2x, y)$:

$$
left(dfrac{1}{10}, -1right)rightarrowleft(dfrac{1}{5}, -1right)
$$

$$
(1, 0)rightarrow(2, 0)
$$

$$
(10, 1)rightarrow(20, 1)
$$

$$
color{#4257b2}text{(III)} g(x)=log_{10}x-5
$$

Adding to the coordinate of $y$ points by $5$ as follows $(x, y)rightarrow(x, y+5)$:

$$
left(dfrac{1}{10}, -1right)rightarrowleft(dfrac{1}{10}, 4right)
$$

$$
(1, 0)rightarrow(1, 5)
$$

$$
(10, 1)rightarrow(10, 6)
$$

$$
color{#4257b2}text{(IV)} g(x)=log_{10}(x+4)
$$

Subtract the coordinate of $x$ points by $-4$ as follows $(x, y)rightarrow(x-4, y)$:

$$
left(dfrac{1}{10}, -1right)rightarrowleft(dfrac{-39}{10}, -1right)
$$

$$
(1, 0)rightarrow(-3, 0)
$$

$$
(10, 1)rightarrow(6, 1)
$$

$$
text{color{#4257b2}(b) State the domain and range for each function in the question $1$.}
$$

(I) Domain $=(0, infty)$ Range$=(-infty, infty)$

(II) Domain $=(0, infty)$ Range$=(-infty, infty)$

(III) Domain $=(0, infty)$ Range$=(-infty, infty)$

(IV) Domain $=(-4, infty)$ Range$=(-infty, infty)$

$$
text{color{#c34632}(a) (I) $left(dfrac{1}{10}, -3right)$ $(1, 0)$ $(10, 3)$
\ \ \
(II) $left(dfrac{1}{5}, -1right)$ $(2, 0)$ $(20, 1)$
\ \ \
(III) $left(dfrac{1}{10}, 4right)$ $(1, 5)$ $(10, 6)$
\ \ \
(IV) $left(dfrac{-39}{10}, -1right)$ $(-3, 0)$ $(6, 1)$
\ \ \
(b) (I) Domain $=(0, infty)$ Range$=(-infty, infty)$
\ \
(II) Domain $=(0, infty)$ Range$=(-infty, infty)$
\ \
(III) Domain $=(0, infty)$ Range$=(-infty, infty)$
\ \
(IV) Domain $=(-4, infty)$ Range$=(-infty, infty)$}
$$

State the equation of the function that results from each of the following pairs of transformation.

$$
color{#4257b2}text{(a)} a=5 c=3
$$

Standard function can be expressed by $f(x)=a log_{10} [k(x-d)]+c$

$$
f(x)=5log_{10}x+3
$$

$$
color{#4257b2}text{(b)} a=-1 k=dfrac{1}{3}
$$

Standard function can be expressed by $f(x)=a log_{10} [k(x-d)]+c$

$$
f(x)=- log_{10}left(dfrac{1}{3}xright)
$$

$$
color{#4257b2}text{(c)} d=-4 c=-3
$$

Standard function can be expressed by $f(x)=a log_{10} [k(x-d)]+c$

$$
f(x)=log_{10} (x-(-4))-3 f(x)=log_{10} (x+4)-3
$$

$$
color{#4257b2}text{(d)} a=-1 d=4
$$

Standard function can be expressed by $f(x)=a log_{10} [k(x-d)]+c$

$$
f(x)=- log_{10} (x-4)
$$

$color{#c34632}text{(a)} f(x)=5log_{10}x+3$ $color{#c34632}text{(b)} f(x)=- log_{10}left(dfrac{1}{3}xright)$

$color{#c34632}text{(b)} f(x)=log_{10} (x+4)-3$ $color{#c34632}text{(b)} f(x)=- log_{10} (x-4)-3$

Answer for the following questions.

$$
color{#4257b2} text{(I)} -4log_{10}(x)+5
$$

$$
text{color{#4257b2} (a) State the transformed that applied for above expression.}
$$

$$
a=-4 c=5
$$

$$
text{color{#4257b2} (b) State the coordinate of the following points for the above expression.}
$$

$$
(1, 0), (10, 1)
$$

Multiply the coordinate of $y$ points by $-4$ as follows:

$$
(x, y)rightarrow(x, -4y)
$$

$$
(1, 0)rightarrow(1, 0)
$$

$$
(10, 1)rightarrow(10, -4)
$$

Then, add to the coordinate of $y$ points by $5$ as follows:

$$
(x, -4y)rightarrow(x, -4y+5)
$$

$$
(1, 0)rightarrow(1, 5)
$$

$$
(10, -4)rightarrow(10, 1)
$$

$$
text{color{#4257b2} (c) State the equation of the symptote for the above expression.}
$$

$$
x=0
$$

$$
text{color{#4257b2} (d) State the domain and range for the above expression.}
$$

Domain $=(0, infty)$ Range $=(-infty, infty)$

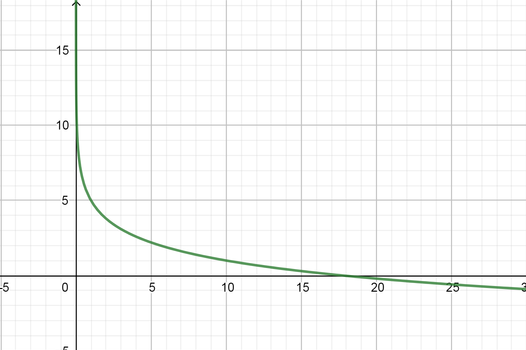
$$
color{#4257b2} text{(II)} dfrac{1}{2}log_{10}(x-6)+3
$$

$$
text{color{#4257b2} (a) State the transformed that applied for above expression.}
$$

$$
k=dfrac{1}{2} d=6 c=3
$$

$$
text{color{#4257b2} (b) State the coordinate of the following points for the above expression.}
$$

$$
(1, 0), (10, 1)
$$

Multiply the coordinate of $y$ points by $left(tfrac{1}{2}right)$ as follows:

$$
(x, y)rightarrowleft(x, dfrac{1}{2}yright)
$$

$$
(1, 0)rightarrow(1, 0)
$$

$$
(10, 1)rightarrow(10, 0.5)
$$

Then, add to the coordinate of $x$ points by $6$ and $y$ points by $3$ as follows:

$$
left(x, dfrac{1}{2}yright)rightarrow left(x+6, dfrac{1}{2}y+3right)
$$

$$
(1, 0)rightarrow(7, 3)
$$

$$
(10, 0.5)rightarrow(16 3.5)
$$

$$
text{color{#4257b2} (c) State the equation of the symptote for the above expression.}
$$

$$
x=6
$$

$$
text{color{#4257b2} (d) State the domain and range for the above expression.}
$$

Domain $=(6, infty)$ Range $=(-infty, infty)$

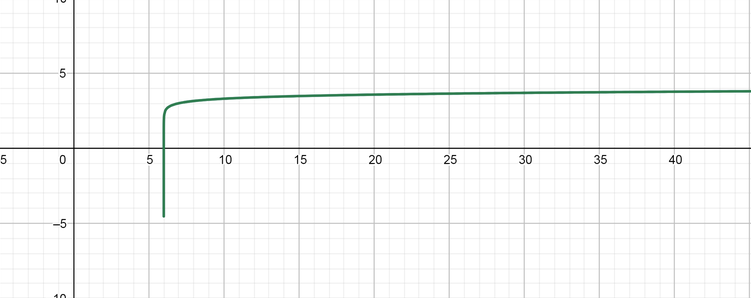
$$
color{#4257b2} text{(III)} log_{10}(3x)-4
$$

$$
text{color{#4257b2} (a) State the transformed that applied for above expression.}
$$

$$
k=3 c=-4
$$

$$
text{color{#4257b2} (b) State the coordinate of the following points for the above expression.}
$$

$$
(1, 0), (10, 1)
$$

Multiply the coordinate of $x$ points by $3$ as follows:

$$
(x, y)rightarrow(3x, y)
$$

$$
(1, 0)rightarrow(3, 0)
$$

$$
(10, 1)rightarrow(30, 1)
$$

Then, subtract to the coordinate of $y$ points by $-4$ as follows:

$$
(3x, y)rightarrow(3x, y-5)
$$

$$
(3, 0)rightarrow(3, -4)
$$

$$
(30, 1)rightarrow(30, -3)
$$

$$
text{color{#4257b2} (c) State the equation of the symptote for the above expression.}
$$

$$
x=0
$$

$$
text{color{#4257b2} (d) State the domain and range for the above expression.}
$$

Domain $=(0, infty)$ Range $=(-infty, infty)$

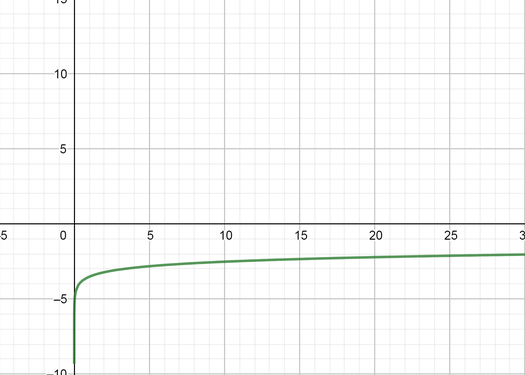
$$
color{#4257b2} text{(IV)} 2log_{10}[-2(x+2)]
$$

$$
text{color{#4257b2} (a) State the transformed that applied for above expression.}
$$

$$
a=2 k=-2 d=-2
$$

$$
text{color{#4257b2} (b) State the coordinate of the following points for the above expression.}
$$

$$
(1, 0), (10, 1)
$$

Multiply the coordinate of $x$ points by $-2$ and $y$ points by $2$ as follows:

$$
(x, y)rightarrow(-2x, 2y)
$$

$$
(1, 0)rightarrow(-2, 0)
$$

$$
(10, 1)rightarrow(-20, 2)
$$

Then, subtract to the coordinate of $x$ points by $-2$ as follows:

$$
(-2x, 2y)rightarrow(-2x-2, 2y)
$$

$$
(-2, 0)rightarrow(-4, 0)
$$

$$
(-20, 2)rightarrow(-22, 2)
$$

$$
text{color{#4257b2} (c) State the equation of the symptote for the above expression.}
$$

$$
x=-2
$$

$$
text{color{#4257b2} (d) State the domain and range for the above expression.}
$$

Domain $=(-2, -infty)$ Range $=(-infty, infty)$

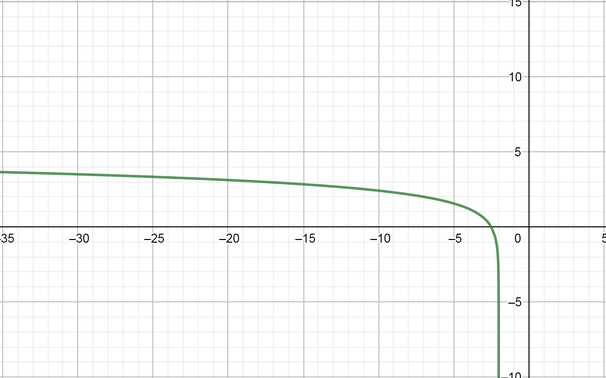
$$
color{#4257b2} text{(V)} log_{10}(2x+4)
$$

$$
text{color{#4257b2} (a) State the transformed that applied for above expression.}
$$

$$
k=2 d=-4
$$

$$
text{color{#4257b2} (b) State the coordinate of the following points for the above expression.}
$$

$$
(1, 0), (10, 1)
$$

Multiply the coordinate of $x$ points by $2$ as follows:

$$
(x, y)rightarrow(2x, y)
$$

$$
(1, 0)rightarrow(2, 0)
$$

$$
(10, 1)rightarrow(20, 1)
$$

Then, subtract to the coordinate of $x$ points by $-4$ as follows:

$$
(2x, y)rightarrow(2x-4, y)
$$

$$
(2, 0)rightarrow(-2, 0)
$$

$$
(20, 1)rightarrow(16, 1)
$$

$$
text{color{#4257b2} (c) State the equation of the symptote for the above expression.}
$$

$$
x=-2
$$

$$
text{color{#4257b2} (d) State the domain and range for the above expression.}
$$

Domain $=(-2, infty)$ Range $=(-infty, infty)$

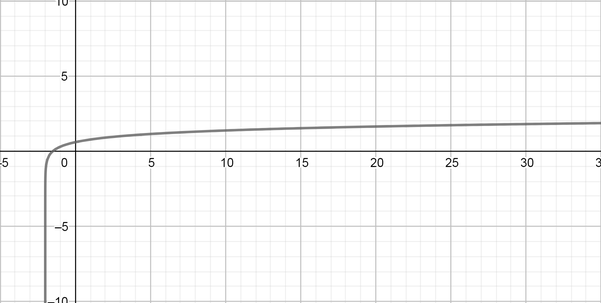
$$
color{#4257b2} text{(VI)} log_{10}(-x-2)
$$

$$
text{color{#4257b2} (a) State the transformed that applied for above expression.}
$$

$$
k=-1 d=2
$$

$$
text{color{#4257b2} (b) State the coordinate of the following points for the above expression.}
$$

$$
(1, 0), (10, 1)
$$

Multiply the coordinate of $x$ points by $-1$ as follows:

$$
(x, y)rightarrow(-x, y)
$$

$$
(1, 0)rightarrow(-1, 0)
$$

$$
(10, 1)rightarrow(-10, 1)
$$

Then, add to the coordinate of $x$ points by $2$ as follows:

$$
(-x, y)rightarrow(-x+2, y)
$$

$$
(-1, 0)rightarrow(1, 0)
$$

$$
(-10, 1)rightarrow(-8, 1)
$$

$$
text{color{#4257b2} (c) State the equation of the symptote for the above expression.}
$$

$$
x=-2
$$

$$
text{color{#4257b2} (d) State the domain and range for the above expression.}
$$

Domain $=(-2, -infty)$ Range $=(-infty, infty)$

{$text{color{#c34632}(a)
\ \
(I) $a=-4, c=5$ (II) $k=dfrac{1}{2}, d=6, c=3$ (III) $k=3, c=-4$
\ \
(IV) $a=2, k=-2, d=-2$ (V) $k=2, d-4$ (III) $k=-1, d=2$
\ \ (b) \ \
(I) $(1, 5), (10, 1)$ (II) $(7, 3), (16, 3.5)$ (III) $(3, -4), (30, -3)$
\ \
(IV) $(-4, 0), (-22, 2)$ (V) $(-2, 0), (16, 1)$ (III) $(1, 0), (-8, 1)$
\ \ (c) \ \
(I) $x=0$ (II) $x=6$ (III) $x=0$
\ \
(IV) $x=-2$ (V) $x=-2$ (III) $x=-2$
\ \ (d) \ \
(I) D=$(0, -infty)$, R$=(-infty, infty)$ (II) D=$(6, infty)$, R$=(-infty, infty)$ \ \ (III) D=$(0, infty)$, R$=(-infty, infty)$ (IV) D=$(-2, -infty)$, R$=(-infty, infty)$
\ \
(V) D=$(-2, infty)$, R$=(-infty, infty)$ (VI) D=$(-2, -infty)$, R$=(-infty, infty)$}$

Graph the following expression, then state the domain and range for each one of the following expression.

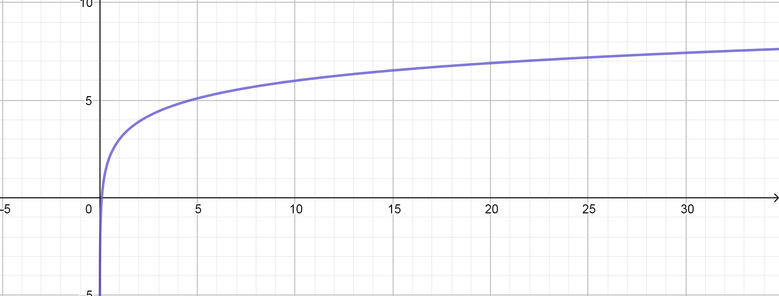
$$
color{#4257b2}text{(a)} 3log_{10}x+3
$$

Domain $= (0, infty)$ Range $=(-infty, infty)$

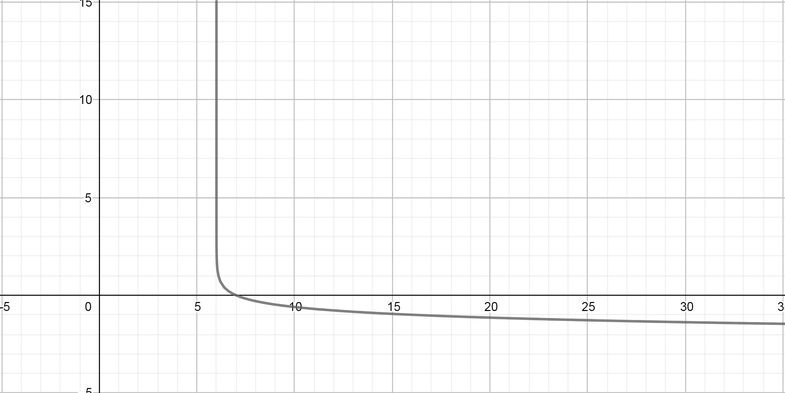
$$
color{#4257b2}text{(b)} -log_{10}(x-6)
$$

Domain $= (6, infty)$ Range $=(-infty, infty)$

$$
color{#4257b2}text{(c)} log_{10}(2x)
$$

Domain $= (0, infty)$ Range $=(-infty, infty)$

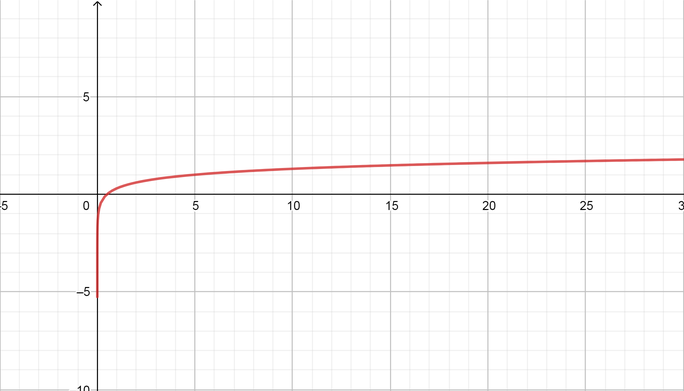
$$
color{#4257b2}text{(d)} log_{10}(0.5x)-1
$$

Domain $= (0, infty)$ Range $=(-infty, infty)$

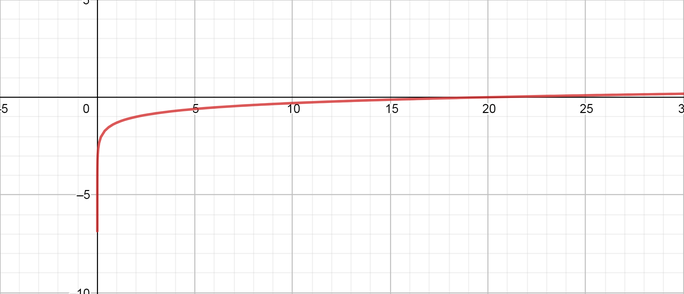
$$
color{#4257b2}text{(e)} 4log_{10}left(dfrac{1}{6}xright)-2
$$

Domain $= (0, infty)$ Range $=(-infty, infty)$

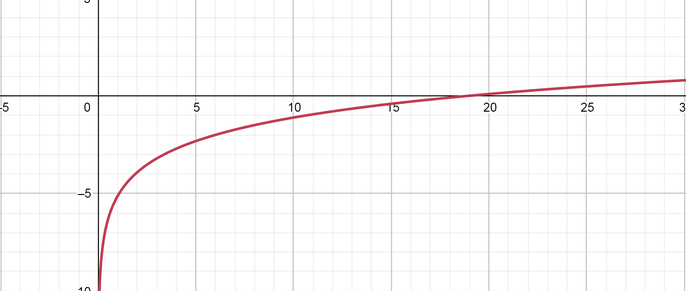
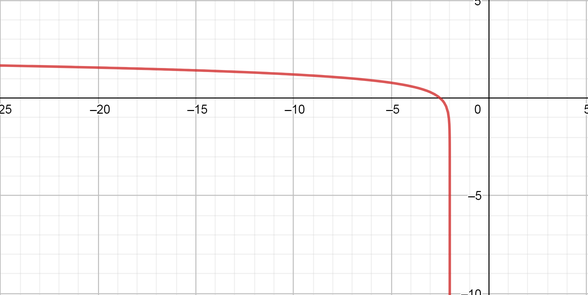
$$
color{#4257b2}text{(f)} log_{10}(-2x-4)
$$

Domain $= (-2, -infty)$ Range $=(-infty, infty)$

$$
text{color{#c34632} (a) Domain $= (0, infty)$ Range $=(-infty, infty)$}
$$

$$
text{color{#c34632} (b) Domain $= (6, infty)$ Range $=(-infty, infty)$}
$$

$$
text{color{#c34632} (c) Domain $= (0, infty)$ Range $=(-infty, infty)$}
$$

$$
text{color{#c34632} (d) Domain $= (0, infty)$ Range $=(-infty, infty)$}
$$

$$
text{color{#c34632} (e) Domain $= (0, infty)$ Range $=(-infty, infty)$}
$$

$$
text{color{#c34632} (f) Domain $= (-2, -infty)$ Range $=(-infty, infty)$}
$$

Compare the function $f(x)=(10)^{tfrac{x}{3}}+1$ and $g(x)=3log_{10}(x-1)$

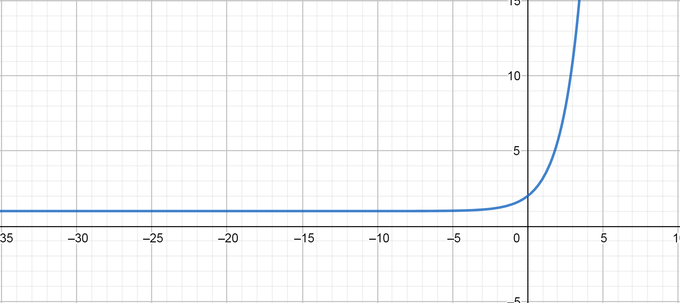
$$
color{#4257b2}f(x)=(10)^{tfrac{x}{3}}+1
$$

Domain $=(-infty, infty)$ Range $=(1, infty)$

Asymptote equation is $y=1$

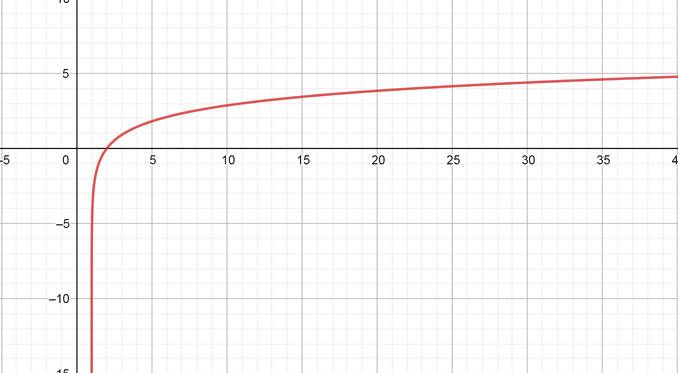
$$
color{#4257b2}g(x)=3log_{10}(x-1)
$$

Domain $=(1, infty)$ Range $=(-infty, infty)$

Asymptote equation is $x=1$

$$
text{color{#c34632}Domain $=(-infty, infty)$ Range $=(1, infty)$ Asymptote equation is $y=1$
\ \
Domain $=(1, infty)$ Range $=(-infty, infty)$ Asymptote equation is $x=1$}
$$

A logarithmic function of the form $f(x)= alog_n(k(x-d))+c$ can be graphed by applying the appropriate transformations to the parent function, $f(x)= log_nx$, where

* $abs{a}$ gives the vertical stretch/compression factor. If $a>1$ it gives vertical stretch, while $0le ale 1$ gives compression by a factor $a$. If $a1$ it gives horizontal compression, while $0le kle 1$ gives stretch by a factor $a$ If $k<0$ there is also a reflection in the $y$-axis.

* $d$ gives the horizontal translation. If $d0$ it translates graph $d$ units to the right.

* $c$ gives the vertical translation. If $c0$ it translates graph $c$ units upward.

Comparing the given functions and using the coefficients $a$, $k$, $d$, and $c$ to describe the transformation of the parent function, we can make a conclusion about the similarities of the graphs of those functions.

*(a)* Note that all three functions are logarithmic functions of the base $3$. Hence, they all have the same general shape.

The given function $f(x)=log_3x$ is a parent function and other functions can be graphed by applying the appropriate transformations to the parent function.

Note that $g(x)=log_3(x+4)$ has a coefficient $d=-4$. Hence, this function is parent function translated $4$ units to the left.

On the other hand, function $h(x)=log_3x+4$ has a coefficient $c=4$. Hence, this function is parent function translated $4$ units upward.

*(b)* Note that all three functions are logarithmic functions of the base $3$. Hence, they all have the same general shape.

The given function $f(x)=log_3x$ is a parent function and other functions can be graphed by applying the appropriate transformations to the parent function.

Note that $m(x)=4log_3x$ has a coefficient $a=4$. Hence, this function is parent function vertically stretched by a factor $4$.

On the other hand, function $n(x)=log_34x$ has a coefficient $k=4$. Hence, this function is parent function horizontally compressed by a factor $frac{1}{4}$.

A logarithmic function of the form $f(x)= alog_n(k(x-d))+c$ can be graphed by applying the appropriate transformations to the parent function, $f(x)= log_nx$, where

* $abs{a}$ gives the vertical stretch/compression factor. If $a>1$ it gives vertical stretch, while $0le ale 1$ gives compression by a factor $a$. If $a1$ it gives horizontal compression, while $0le kle 1$ gives stretch by a factor $a$ If $k<0$ there is also a reflection in the $y$-axis.

* $d$ gives the horizontal translation. If $d0$ it translates graph $d$ units to the right.

* $c$ gives the vertical translation. If $c0$ it translates graph $c$ units upward.

Using the coefficients $a$, $k$, $d$, and $c$ to describe the transformation of the parent function, we can conclude the equation of the transformed function.

Each point of the graph of the parent function after transformation becomes
$$
(x,y)toleft(dfrac{1}{k} cdot x+d,ay+cright)tag{1}$$

The vertical asymptote changes when a horizontal translation is applied. The domain of a transformed logarithmic function depends on where the vertical asymptote is located and whether the function is to the left or the right of the vertical asymptote. If the function is to the left of the asymptote $x=d$, the domain is $xd$.

*(a)* When the parent function is vertically stretched by a factor of $3$ and reflected about the $x$-axis, that gives $a=-3$. Horizontal stretch by a factor $2$ gives $frac{1}{k}=2implies k=frac{1}{2}$. Horizontal translation $5$ units to the right gives $d=5$, while vertical translation $2$ units up gives $c=2$. Transformed function now has an equation of a form
$$
begin{align*}
g(x)&=alog_{10}left(k(x-d) right)+c\
&=-3log_{10}left(dfrac{1}{2}(x-5) right)+2
end{align*}$$

*(b)* Using Eq. $(1)$ we can obtain coordinates of the point $(10,1)$ after applied transformations. It yields
$$
(10,1)to(2cdot10+5,-3cdot1+2)=(25,-1)

*(c)* Since the given function is translated $5$ units to the right, the vertical asymptote is now $x=5$, and the graph of the transformed function is right of this asymptote. Hence, domain becomes
$$
D={xinR| x>5},$$
while the range remains unchanged
$$
R={yin R}$$

a) $g(x)==-3log_{10}left(frac{1}{2}(x-5) right)+2$
b) $(25,-1)$
c) $D={xinR| x>5}, R={yin R}$

State the transformation that needed to turn the

$f(x)=4log_{10}(x-4)$ intto the $f(x)=-2log_{10}(x+1)$

To get the value of vertical stretch equal $-2$, should add $-6$ to the original value.

$$
a=4-6=-2
$$

To get the value of horizontal translated equal $1$ unit down, should add $-5$ to the original value.

$$
d=4-5=-1
$$

$$
color{#4257b2}f(x)=(4-6)log_{10}[x-(4-5)]
$$

$$
f(x)=-2log_{10}(x+1)
$$

$$
color{#c34632}f(x)=(4-6)log_{10}(x-(4-5))
$$

State the three characteristics of the function of $f(x)=log_{10}(x)$ that are unchanged under the following transformation terms below.

$$
a=4 k=dfrac{1}{2}
$$

Standard transformation form is $f(x)=alog_{10}[k(x-d)]+c$

$$
f(x)=4log_{10}left(dfrac{1}{2}xright)
$$

The characteristics are:

Domain $=(0, infty)$ Range $=(-infty, infty)$

Asymptote equation is $x=0$

$$
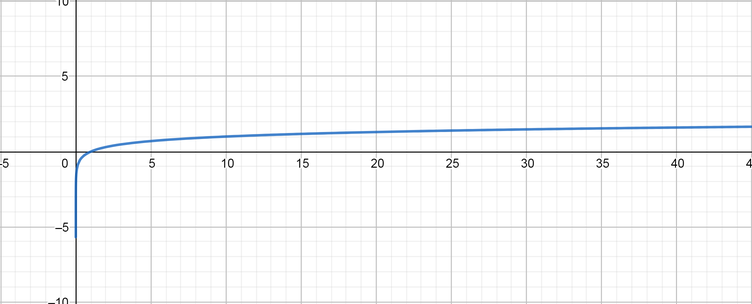
color{#4257b2}f(x)=log_{10}(x)
$$

$$
color{#4257b2}f(x)=4log_{10}(0.5x)
$$

$$
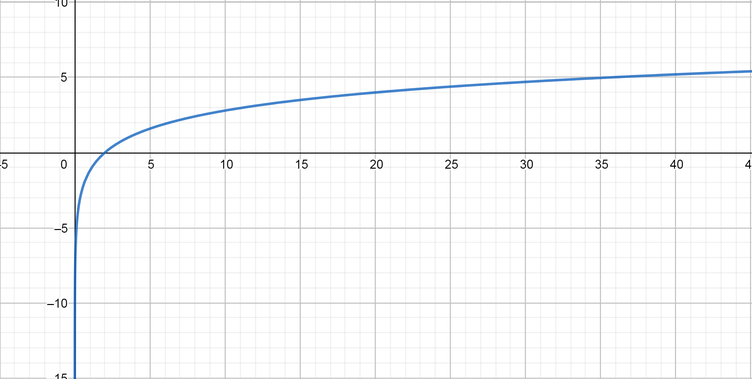
text{color{#c34632}Domain $=(0, infty)$ Range $=(-infty, infty)$
\ \
Asymptote equation is $x=0$}
$$

Sketch the graph.

$$
color{#4257b2}f(x)=dfrac{-2}{log_2(x+2)}
$$

$$
f(x)=-2cdot dfrac{1}{log_2(x+2)}
$$

$$
text{color{#c34632}Large See the graph}
$$