Sketch a graph of the inverse function for the following exponent function.

$$
color{#4257b2}text{(a)} f(x)=4^x
$$

Inverse function standard form $y=a^x x=a^y$

which equivalent the form of $y=log_a x$

$$
text{Inverse function}=log_4x
$$

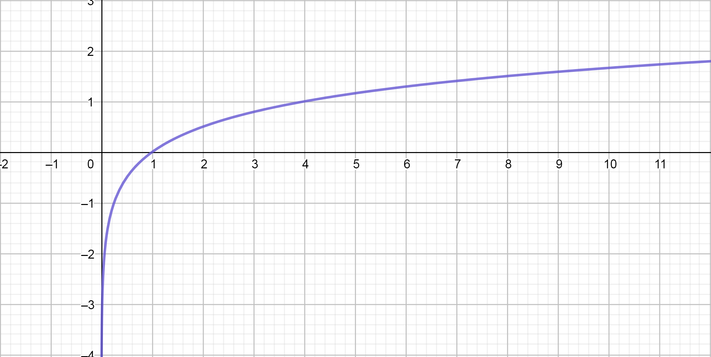
$$
color{#4257b2}text{(b)} f(x)=8^x
$$

Inverse function standard form $y=a^x x=a^y$

which equivalent the form of $y=log_a x$

$$
text{Inverse function}=log_8x
$$

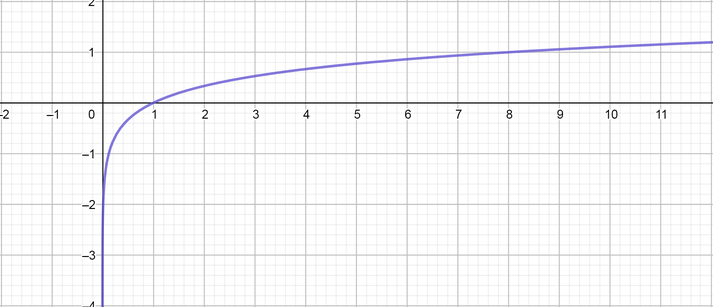
$$
color{#4257b2}text{(c)} f(x)=left(dfrac{1}{3}right)^x
$$

Inverse function standard form $y=a^x x=a^y$

which equivalent the form of $y=log_a x$

$$
text{Inverse function}=log_{tfrac{1}{3}}x
$$

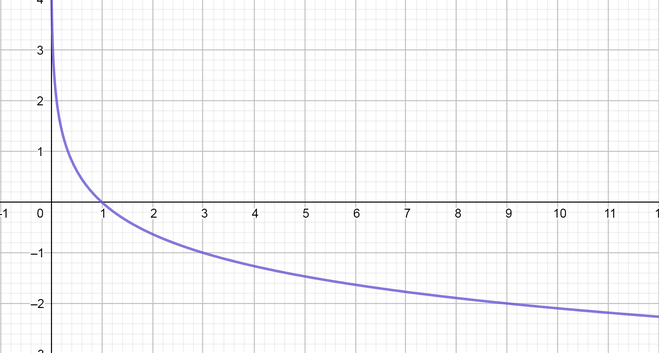
$$
color{#4257b2}text{(d)} f(x)=left(dfrac{1}{5}right)^x
$$

Inverse function standard form $y=a^x x=a^y$

which equivalent the form of $y=log_a x$

$$
text{Inverse function}=log_{tfrac{1}{5}}x
$$

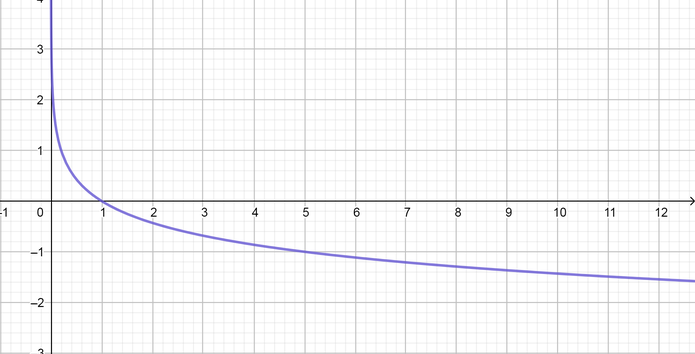
$$
text{color{#c34632}(a) $text{Inverse function}=log_4x$ (b) $text{Inverse function}=log_8x$
\ \
(c) $text{Inverse function}=log_{tfrac{1}{3}}x$ (d) $text{Inverse function}=log_{tfrac{1}{5}}x$}
$$

[2.i] We would like to write the equation of each inverse function of the following exponential functions $text{underline{in exponential form}}$:

$lozenge$ First, we have to know that: the inverse of the exponential function ${color{#4257b2}y=a^{x}}$ can be written as ${color{#4257b2}x=a^{y}}$ and (this is the exponential form of the inverse.)

$text{color{#4257b2}(a) $f(x)=4^{x}$}$

The equation of the inverse of this exponential function can be written in the exponential form directly as:

$$
x=4^{f(x)}
$$

$text{color{#4257b2}(b) $f(x)=8^{x}$}$

The equation of the inverse of this exponential function can be written in the exponential form directly as:

$$
x=8^{f(x)}
$$

$text{color{#4257b2}(c) $f(x)=left(dfrac{1}{3}right)^{x}$}$

The equation of the inverse of this exponential function can be written in the exponential form directly as:

$$
x=left(dfrac{1}{3}right)^{f(x)}
$$

$text{color{#4257b2}(d) $f(x)=left(dfrac{1}{5}right)^{x}$}$

The equation of the inverse of this exponential function can be written in the exponential form directly as:

$$
x=left(dfrac{1}{5}right)^{f(x)}
$$

[2.ii] We would like to write the equation of each inverse function of the following exponential functions $text{underline{in logarithmic form}}$:

$lozenge$ First, we have to know that:

$star$ The inverse of the exponential function ${color{#4257b2}y=a^{x}}$ can be written as ${color{#4257b2}x=a^{y}}$ and (this is the exponential form of the inverse.)

$star$ To convert from exponential form to logarithmic form, and vice versa we can use the definition of a logarithm which state that:

$$
color{#4257b2}boxed{ y=log_{a} x text{color{Black}Is equivalent to} x=a^{y} }
$$

where $a>0$ and $a neq 0$.

$text{color{#4257b2}(a) $f(x)=4^{x}$}$

First, we write the inverse of this exponential function in the exponential form directly as follows:

$$
x=4^{f(x)}
$$

Then we use the definition of a logarithm to convert this exponential function to the logarithmic form as follows:

$$
x=4^{f(x)} text{Is equivalent to} f(x)=log_{4} x
$$

$text{color{#4257b2}(b) $f(x)=4^{x}$}$

First, we write the inverse of this exponential function in the exponential form directly as follows:

$$
x=8^{f(x)}
$$

Then we use the definition of a logarithm to convert this exponential function to the logarithmic form as follows:

$$
x=8^{f(x)} text{Is equivalent to} f(x)=log_{8} x
$$

$text{color{#4257b2}(c) $f(x)=left(dfrac{1}{3}right)^{x}$}$

First, we write the inverse of this exponential function in the exponential form directly as follows:

$$
x=left(dfrac{1}{3}right)^{f(x)}
$$

Then we will use the definition of a logarithm to convert this exponential function to the logarithmic form as follows:

$$
x=left(dfrac{1}{3}right)^{f(x)} text{Is equivalent to} f(x)=log_{tfrac{1}{3}} x
$$

$text{color{#4257b2}(d) $f(x)=left(dfrac{1}{5}right)^{x}$}$

First, we write the inverse of this exponential function in the exponential form directly as follows:

$$
x=left(dfrac{1}{5}right)^{f(x)}
$$

Then we will use the definition of a logarithm to convert this exponential function to the logarithmic form as follows:

$$
x=left(dfrac{1}{5}right)^{f(x)} text{Is equivalent to} f(x)=log_{tfrac{1}{5}} x
$$

$$
text{color{#c34632} [i] a) $x=4^{f(x)}$ b) $x=8^{f(x)}$ c) $x=left(dfrac{1}{3}right)^{f(x)}$ d) $x=left(dfrac{1}{5}right)^{f(x)}$ \ \

[ii] a) $f(x)=log_{4} x$ b) $f(x)=log_{8} x$ c) $f(x)=log_{tfrac{1}{3}} x$ d) $f(x)=log_{tfrac{1}{5}} x$}
$$

We need to compare of the features keys in the ques. $1$.

In the question $1$ after graph the inverse function for each exponential function, we can conclusion the common features for the inverse function graphs.

Domain $(0, infty)$

Range $(-infty, infty)$

Equation of horizontal asymptote s $x$ axis $y=0$

$$
text{color{#c34632}Domain $(0, infty)$
\ \
Range $(-infty, infty)$
\ \
Equation of horizontal asymptote s $x$ axis $y=0$}
$$

We need to solve the following expression by using the graph in the textbook.

$$
2^y=8\ text{Note that} 2^3=8
$$

$$
2^y=2^3
$$

The base of the exponential is equal, so $y=3$

From the graph when intercept the $x$ axis at point $x=8$, we get the value of $y$ which equal $y=3$

$$
text{color{#c34632} $y=3$}
$$

We would like to write the equation of the inverse of the following exponential functions $text{underline{in exponential form:}}$

$lozenge$ First, we have to know that:

$$
color{#4257b2}boxed{ text{The inverse of the exponential function} {color{Black}y=a^{x}} text{can be written as} {color{Black}x=a^{y}} }
$$

(And this is the exponential form of the inverse)

$text{color{#4257b2}(a) $ y=3^{x}$}$

The equation of the inverse of this exponential function can be written in the exponential form directly by using the above note as:

$$
x=3^{y}
$$

$text{color{#4257b2}(b) $ y=10^{x}$}$

The equation of the inverse of this exponential function can be written in the exponential form directly as:

$$
x=10^{y}
$$

$text{color{#4257b2}(c) $ y=left(dfrac{1}{4}right)^{x}$}$

The equation of the inverse of this exponential function can be written in the exponential form directly as:

$$
x=left(dfrac{1}{4}right)^{y}
$$

$text{color{#4257b2}(d) $ y= m^{x}$}$

The equation of the inverse of this exponential function can be written in the exponential form directly as:

$$
x= m^{y}
$$

$text{$text{color{#c34632} a) $x=3^{y}$ b) $x=10^{y}$ c) $x=left(frac{1}{4}right)^{y}$ d) $x=m^{y}$ \ \}$}$

We would like to write the equation of the inverse of the following exponential functions in logarithmic form:

$lozenge$ First, we have to know that:

$star$ The inverse of the exponential function $y=a^{x}$

$$
color{#4257b2}boxed{ {color{Black}y=a^{x}} text{the inverse of} {color{Black}x=a^{y}} text{(This is the exponential form of the inverse)} }
$$

$star$ To convert from exponential form to logarithmic form, and vice versa we can use the definition of a logarithm which state that:

$$
color{#4257b2}boxed{ y=log_{a} x text{color{Black}Is equivalent to} x=a^{y} }
$$

where $a>0$ and $a neq 0$.

$text{color{#4257b2}(a) $ y=3^{x}$}$

First, we write the inverse of this exponential function in the exponential form as follows:

$$
x=3^{y}
$$

Then we use the definition of a logarithm to convert this exponential function to the logarithmic form as follows:

$$
x=3^{y} text{Is equivalent to} y=log_{3} x
$$

$text{color{#4257b2}(b) $ y=10^{x}$}$

First, we write the inverse of this exponential function in the exponential form as follows:

$$
x=10^{y}
$$

Then we use the definition of a logarithm to convert this exponential function to the logarithmic form as follows:

$$
x=10^{y} text{Is equivalent to} y=log_{10} x
$$

$text{color{#4257b2}(c) $ y =left(dfrac{1}{4}right)^{x}$}$

First, we write the inverse of this exponential function in the exponential form as follows:

$$
x=left(dfrac{1}{4}right)^{y}
$$

Then we will use the definition of a logarithm to convert this exponential function to the logarithmic form as follows:

$$
x=left(dfrac{1}{4}right)^{y} text{Is equivalent to} y=log_{tfrac{1}{4}} x
$$

$text{color{#4257b2}(d) $ y= m^{x}$}$

First, we write the inverse of this exponential function in the exponential form as follows:

$$
x= m^{y}
$$

Then we will use the definition of a logarithm to convert this exponential function to the logarithmic form as follows:

$$
x= m^{y} text{Is equivalent to} y=log_{m} x
$$

$$
text{color{#c34632} a) $y=log_{3} x$ b) $y=log_{10} x$\ \

c) $ y=log_{tfrac{1}{4}} x$ d) $y=log_{m} x$}
$$

We would like to write the equation of each of the following logarithmic functions in exponential form:

$lozenge$ First, we have to know that:

$star$ To convert from exponential form to logarithmic form, and vice versa we can use the definition of a logarithm which state that:

$$
color{#4257b2}boxed{ y=log_{a} x text{color{Black}Is equivalent to} x=a^{y} }
$$

where $a>0$ and $a neq 0$.

$text{color{#4257b2}(a) $ y=log_{5} x$}$

To convert this logarithmic function to the exponential form we will use the definition of a logarithm as follows:

$$
y=log_{5} x text{Is equivalent to} x=5^{y}
$$

$text{color{#4257b2}(b) $ y=log_{10} x $}$

To convert this logarithmic function to the exponential form we will use the definition of a logarithm as follows:

$$
y=log_{10} x text{Is equivalent to} x=10^{y}
$$

$text{color{#4257b2}(c) $ y=log_{3} x $}$

To convert this logarithmic function to the exponential form we will use the definition of a logarithm as follows:

$$
y=log_{3} x text{Is equivalent to} x=3^{y}
$$

$text{color{#4257b2}(d) $ y= log_{tfrac{1}{4}} x $}$

To convert this logarithmic function to the exponential form we will use the definition of a logarithm as follows:

$$
y=log_{tfrac{1}{4}} x text{Is equivalent to} x=left(dfrac{1}{4}right)^{y}
$$

$$
text{color{#c34632} a) $x=5^{y}$ b) $x=10^{y}$ \ \

c) $x=3^{y}$ d) $x=left(frac{1}{4}right)^{y}$}
$$

We would like to write the equation of the inverse of each logarithmic function in exponential form:

$lozenge$ First, we have to know that:

$star$ The inverse of the logarithmic function $y=log_{a} x$

$$
color{#4257b2}boxed{ y=log_{a} x text{the inverse of} x=log_{a} y }
$$

$star$ To convert from exponential form to logarithmic form, and vice versa we can use the definition of a logarithm which state that:

$$
color{#4257b2}boxed{ y=log_{a} x text{color{Black}Is equivalent to} x=a^{y} }
$$

where $a>0$ and $a neq 0$.

$text{color{#4257b2}(a) $ y=log_{5} x $}$

First, we write the inverse of this logarithmic function as follows:

$$
x=log_{5} y
$$

Then we will use the definition of a logarithm to convert this logarithmic function to the exponential form as follows:

$$
x=log_{5} y text{Is equivalent to} y=5^{x}
$$

$text{color{#4257b2}(b) $ y=log_{10} x$}$

First, we write the inverse of this logarithmic function as follows:

$$
x=log_{10} y
$$

Then we will use the definition of a logarithm to convert this logarithmic function to the exponential form as follows:

$$
x=log_{10} y text{Is equivalent to} y=10^{x}
$$

$text{color{#4257b2}(c) $ y=log_{3} x$}$

First, we write the inverse of this logarithmic function as follows:

$$
x=log_{3} y
$$

Then we will use the definition of a logarithm to convert this logarithmic function to the exponential form as follows:

$$
x=log_{3} y text{Is equivalent to} y=3^{x}
$$

$text{color{#4257b2}(d) $ y=log_{tfrac{1}{4}} x$}$

First, we write the inverse of this logarithmic function as follows:

$$
x=log_{tfrac{1}{4}} y
$$

Then we will use the definition of a logarithm to convert this logarithmic function to the exponential form as follows:

$$
x=log_{tfrac{1}{4}} y text{Is equivalent to} y=left(dfrac{1}{4}right)^{x}
$$

$$
text{color{#c34632} a) $y=5^{x}$ b) $y=10^{x}$ \ \

c) $y=3^{x}$ d) $y=left(frac{1}{4}right)^{x}$}
$$

We would like to evaluate each of the following:

$lozenge$ First, we have to know that:

$star$ To convert from exponential form to logarithmic form, and vice versa we can use the definition of a logarithm which state that:

$$
color{#4257b2}boxed{ y=log_{a} x text{color{Black}Is equivalent to} x=a^{y} }
$$

where $a>0$ and $a neq 0$.

(a) $log_{2} 4$

First, we will convert this logarithm to the exponential form by using the definition of a logarithm as follows:

$$
color{#4257b2} y=log_{2} 4 text{Is equivalent to} 2^{y}=4
$$

Then we will think like this “2 raised to what power yields 4”. So,

$$
because 2^{y}=4
$$

$$
therefore 2^{y}= 2^{2} therefore y= 2
$$

$$
color{#4257b2}because log_{2} 4= y therefore log_{2} 4= 2
$$

(b) $log_{3} 27$

First, we will convert this logarithm to the exponential form by using the definition of a logarithm as follows:

$$
color{#4257b2} y=log_{3} 27 text{Is equivalent to} 3^{y}=27
$$

Then we will think like this “3 raised to what power yields 27”. So,

$$
because 3^{y}=27
$$

$$
therefore 3^{y}= 3^{3} therefore y= 3
$$

$$
color{#4257b2}because log_{3} 27= y therefore log_{3} 27= 3
$$

(c) $log_{4} 64$

First, we will convert this logarithm to the exponential form by using the definition of a logarithm as follows:

$$
color{#4257b2} y=log_{4} 64 text{Is equivalent to} 4^{y}=64
$$

Then we will think like this “4 raised to what power yields 64”. So,

$$
because 4^{y}=64
$$

$$
therefore 4^{y}= 4^{3} therefore y= 3
$$

$$
color{#4257b2}because log_{4} 64= y therefore log_{4} 64= 3
$$

(d) $log_{5} 1$

First, we will convert this logarithm to the exponential form by using the definition of a logarithm as follows:

$$
color{#4257b2} y=log_{5} 1 text{Is equivalent to} 5^{y}= 1
$$

Then we will think like this “5 raised to what power yields 1”. So,

$$
because 5^{y}=1
$$

$$
therefore 5^{y}= 5^{0} therefore y= 0
$$

$$
color{#4257b2}because log_{5} 1= y therefore log_{5} 1= 0
$$

(e) $log_{2} left(tfrac{1}{2}right)$

First, we will convert this logarithm to the exponential form by using the definition of a logarithm as follows:

$$
color{#4257b2} y=log_{2} left(tfrac{1}{2}right) text{Is equivalent to} 2^{y}=tfrac{1}{2}
$$

Then we will think like this “2 raised to what power yields $tfrac{1}{2}$”. So,

$$
because 2^{y}=tfrac{1}{2}
$$

$$
therefore 2^{y}= 2^{-1} therefore y= -1
$$

$$
color{#4257b2}because log_{2} left(tfrac{1}{2}right)= y therefore log_{2} left(tfrac{1}{2}right)= -1
$$

(f) $log_{3} sqrt{3}$

First, we will convert this logarithm to the exponential form by using the definition of a logarithm as follows:

$$
color{#4257b2} y=log_{3} sqrt{3} text{Is equivalent to} 3^{y}= sqrt{3}
$$

Then we will think like this “3 raised to what power yields $sqrt{3}$”. So,

$$
because 3^{y}=sqrt{3}
$$

$$
therefore 3^{y}=3^{tfrac{1}{2}} therefore y= dfrac{1}{2}
$$

$$
color{#4257b2}because log_{3} sqrt{3}= y therefore log_{3} sqrt{3}= dfrac{1}{2}
$$

$$
text{color{#c34632} a) $log_{2} 4=2$ b) $log_{3} 27=3$ c) $log_{4} 64=3$ \ \

d) $log_{5} 1=0$ e) $log_{2} tfrac{1}{2}=-1$ f) $log_{3} sqrt{3}=dfrac{1}{2}$}
$$

$lozenge$ First, we have to know that:

$star$ To convert from exponential form to logarithmic form, and vice versa we can use the definition of a logarithm which state that:

$$
color{#4257b2}boxed{ y=log_{a} x text{color{Black}Is equivalent to} x=a^{y} }
$$

$text{underline{where $a>0$ and $a neq 0$.}}$

$lozenge$ Now the $log_{3} (-9)$ can not be evaluated because $(-9 < 0)$, so we can not convert this logarithm to exponential form to evaluate it.

(As we know the first step to evaluate any logarithm is convert this logarithm to exponential form.)

$$
text{color{#c34632} For this reason $(-9 < 0).$}
$$

Write the coordinates of the points that have $y$ values is $[-2, -1, 0, 1, 2]$ for the following expressions.

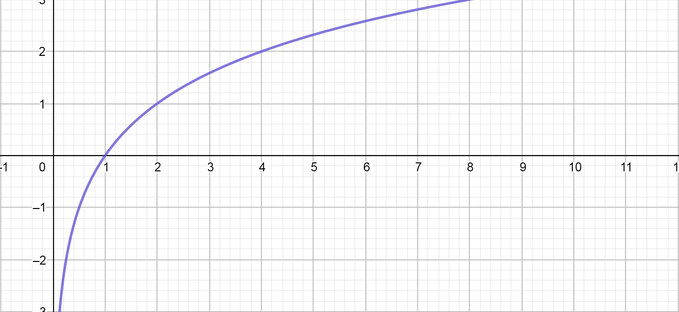
$$
color{#4257b2}text{(a)} y=log_2 x
$$

Now we graph the function, then intercept these point at $y$ axis to complete the points as follows:

$$
(-2, 0.2), (-1, 0.5), (0, 1), (1, 2), (2, 4)
$$

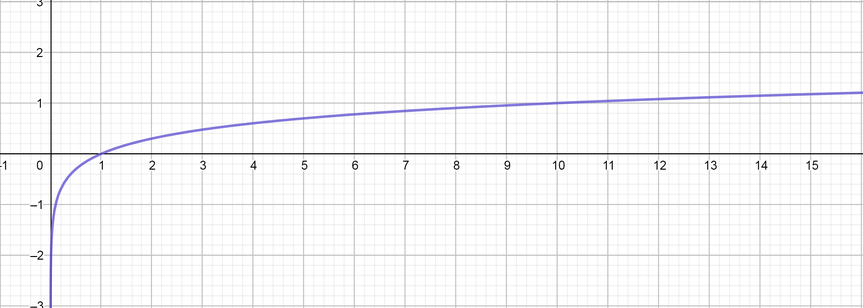
$$
color{#4257b2}text{(b)} y=log_10 x
$$

Now we graph the function, then intercept these point at $y$ axis to complete the points as follows:

$$
(-2, 0), (-1, 0.1), (0, 1), (1, 10), (2, 50)
$$

$$
text{color{#c34632}(a) $(-2, 0.2), (-1, .05), (0, 1), (1, 2), (2, 4)$
\ \
(b) $(-2, 0), (-1, 0.1), (0, 1), (1, 10), (2, 50)$}
$$