We would like to use a counterexample to disapprove that $color{#4257b2}sin x=cos x$ is an identity. Since we need to prove that $color{#4257b2}sin x=cos x$ is not an identity, we can substitute $color{#4257b2}x=0$ and show if $color{#4257b2}sin x$ will equal $color{#4257b2}cos x$ or not.

$$
sin x=cos x
$$

$$
sin 0=cos 0
$$

$$
0=1
$$

Note that the angle $color{#4257b2}0$ is a special angle which we know the values of the sine and cosine functions for it where $color{#4257b2}sin 0=0$ and $color{#4257b2}cos 0=1$

We note that the value of $color{#4257b2}sin 0$ does not equal the value of $color{#4257b2}cos 0$,
so $color{#4257b2}sin x=cos x$ is not an identity.

$color{#c34632}sin x=cos xis not an identity$

We would like to graph the two functions $color{#4257b2}f(x)=sin x$ and $color{#4257b2}g(x)=tan xcos x$. We can use the graphing calculator to graph them as follows:

(b) From the two graphs of $color{#4257b2}f(x)$ and $color{#4257b2}g(x)$ we note that the two functions are the same, so we can write the trigonometric identity $color{#4257b2}sin x=tan xcos x$

(c) We would like to simplify one side to prove that the identity is true. We can simplify the right side $color{#4257b2}tan xcos x$. First, we know the identity $color{#4257b2}tan x=dfrac{sin x}{cos x}$, so we can replace $color{#4257b2}tan x$ from the right side by $color{#4257b2}dfrac{sin x}{cos x}$

$$
begin{align*}
RS&=tan xcos x
\ \
&=dfrac{sin x}{cos x}cdot cos x
\ \
&=dfrac{sin x}{cancel{cos x}}cdot cancel{cos x}
\ \
&=sin x
end{align*}
$$

So we proved that the right side = the left side.

(d) The identity is true for all real numbers, except where $color{#4257b2}cos x=0$ because in this case $color{#4257b2}tan x$ will be undefined where $color{#4257b2}tan x=dfrac{sin x}{cos x}$ and if $color{#4257b2}cos x=0$ that means that the denominator of $color{#4257b2}tan x$ equals zero which is undefined.

$$
text{color{#c34632}$sin x=tan xcos x$, where $cos x ne 0$}
$$

We would like to graph the appropriate functions to match each expression on the left with the equivalent expression on the right. First, we will graph the functions on the left and then graph the functions on the right to match between each expression.

For the graphs on the left:

$$
text{color{#4257b2}(a)}
$$

$$
text{color{#4257b2}(b)}
$$

$$
text{color{#4257b2}(c)}
$$

$$
text{color{#4257b2}(d)}
$$

Now we will graph the functions on the right and then compare the functions on the left with the functions on the right to know which is equivalent to the other

$color{#4257b2}$A

$color{#4257b2}$B

$color{#4257b2}$C

$color{#4257b2}$D

By comparing the graphs of the functions on the left with the graphs of the functions on the right we see that the function $text{color{#4257b2}(a)}$ from the left is equivalent to the function $text{color{#4257b2}C}$ from the right, the function $text{color{#4257b2}(b)}$ from the left is equivalent to the function $text{color{#4257b2}D}$ from the right, the function $text{color{#4257b2}(c)}$ from the left is equivalent to the function $text{color{#4257b2}B}$ from the right and the function $text{color{#4257b2}(d)}$ from the left is equivalent to the function $text{color{#4257b2}A}$ from the right

$$
text{color{#c34632}(a) C (b) D (c) B (d) A}
$$

We would like to prove that the expressions we matched in question $3$ are equivalent, so we will prove each identity as follows:

For the first identity $color{#4257b2}(a) sin xcot x=(C) cos x$, we can simplify the left side where we know that $color{#4257b2}cot x=dfrac{cos x}{sin x}$.

$$
begin{align*}
sin xcot x&=sin xcdot dfrac{cos x}{sin x}
\ \
&=cancel{sin x}cdot dfrac{cos x}{cancel{sin x}}
\ \
&=cos x
end{align*}
$$

So we prove that the left side equals $color{#4257b2}cos x$ which means that the left side is equivalent to the right side.

For the second identity $color{#4257b2}(b) 1-2sin^{2}x=(D) 2cos^{2}x-1$, we can simplify the left side where we know that $color{#4257b2}sin^{2}x+cos^{2}x=1$, so $color{#4257b2}sin^{2}x=1-cos^{2}x$.

$$
begin{align*}
1-2sin^{2}x&=1-2left(1-cos^{2}xright)
\ \
&=1-2+2cos^{2}x
\ \
&=2cos^{2}x-1
end{align*}
$$

So we prove that the left side equals $color{#4257b2}2cos^{2}x-1$ which means that the left side is equivalent to the right side.

For the third identity $color{#4257b2}(c) left(sin x+cos xright)^{2}=(B) 1+2sin xcos x$, we can simplify the left side by distributing the exponent where we know that $color{#4257b2}left(a+bright){2}=a^{2}+2ab+b^{2}$.

$$
begin{align*}
left(sin x+cos xright)^{2}&= sin^{2}x+2sin xcos x+cos^{2}x
\ \
&= left(sin^{2}x+cos^{2}xright)+2sin xcos x
\ \
&=1+2sin xcos x
end{align*}
$$

Note that we know from the Pythagorean identity that $color{#4257b2}sin^{2}x+cos^{2}x=1$

So we prove that the left side equals $color{#4257b2}1+2sin xcos x$ which means that the left side is equivalent to the right side.

For the fourth identity $color{#4257b2}(d) sec^{2}x=(A) sin^{2}x+cos^{2}x+tan^{2}x$, we can simplify the right side where we know from the Pythagorean identity that $color{#4257b2}sin^{2}x+cos^{2}x=1$.

$$
begin{align*}
sin^{2}x+cos^{2}x+tan^{2}x&= 1+tan^{2}x
\ \
&=sec^{2}x
end{align*}
$$

Note that we know from the Pythagorean identity that $color{#4257b2}1+tan^{2}x=sec^{2}x$

So we prove that the right side equals $color{#4257b2}sec^{2}x$ which means that the right side is equivalent to the left side.

$$
text{color{#c34632}(a) is equivalent to C (b) is equivalent to D
\
\
Large{color{#c34632}(c) is equivalent to B (d) is equivalent to A}}
$$

(a) We would like to use a counterexample to show that the equation $color{#4257b2}cos x=dfrac{1}{cos x}$ is not an identity. Since we need to prove that $color{#4257b2}cos x=dfrac{1}{cos x}$ is not an identity, we can substitute $color{#4257b2}x=60text{textdegree}$ and show if $color{#4257b2}cos x$ will equal $color{#4257b2}dfrac{1}{cos x}$ or not.

$$
cos x=dfrac{1}{cos x}
$$

$$
cos 60text{textdegree}=dfrac{1}{cos 60text{textdegree}}
$$

$$
dfrac{1}{2}=dfrac{1}{dfrac{1}{2}}
$$

$$
dfrac{1}{2}=2
$$

Note that the angle $color{#4257b2}60text{textdegree}$ is a special angle which we know the value of the cosine function for it where $color{#4257b2}cos 60text{textdegree}=dfrac{1}{2}$

We note that the value of $color{#4257b2}cos 60text{textdegree}$ does not equal the value of $color{#4257b2}dfrac{1}{cos 60text{textdegree}}$, so the equation $color{#4257b2}cos x=dfrac{1}{cos x}$ is not an identity.

(b) We would like to use a counterexample to show that the equation $color{#4257b2}1-tan^{2}x=sec^{2}x$ is not an identity. Since we need to prove that
$color{#4257b2}1-tan^{2}x=sec^{2}x$ is not an identity, we can substitute $color{#4257b2}x=45text{textdegree}$ and show if $color{#4257b2}1-tan^{2}x$ will equal $color{#4257b2}sec^{2}x$ or not.

$$
1-tan^{2}x=sec^{2}x
$$

$$
1-tan^{2}45text{textdegree}=sec^{2}45text{textdegree}
$$

$$
1-1^{2}=left(sqrt{2}right)^{2}
$$

$$
1-1=2
$$

$$
0=2
$$

Note that the angle $color{#4257b2}45text{textdegree}$ is a special angle which we know the values of the tangent and secant functions for it where $color{#4257b2}tan 45text{textdegree}=1$ and $color{#4257b2}sec 45text{textdegree}=sqrt{2}$

We note that the value of $color{#4257b2}1-tan^{2}45text{textdegree}$ does not equal the value of $color{#4257b2}sec^{2}45text{textdegree}$, so the equation $color{#4257b2}1-tan^{2}x=sec^{2}x$ is not an identity.

(c) We would like to use a counterexample to show that the equation $color{#4257b2}sin left(x+yright)=cos xcos y+sin xsin y$ is not an identity. Since we need to prove that $color{#4257b2}sin left(x+yright)=cos xcos y+sin xsin y$ is not an identity, we can substitute $color{#4257b2}x=0text{textdegree}$ and $color{#4257b2}y=90text{textdegree}$ and show if $color{#4257b2}sin left(x+yright)$ will equal $color{#4257b2}cos xcos y+sin xsin y$ or not.

$$
sin left(x+yright)=cos xcos y+sin xsin y
$$

$$
sin left(0text{textdegree}+90text{textdegree}right)=cos 0text{textdegree}cos 90text{textdegree}+sin 0text{textdegree}sin 90text{textdegree}
$$

$$
sin 90text{textdegree}=1cdot 0+0cdot 1
$$

$$
1=0+0
$$

$$
1=0
$$

Note that the angles $color{#4257b2}0text{textdegree}$ and $color{#4257b2}90text{textdegree}$ are special angles which we know the values of the sine and cosine functions for it where $color{#4257b2}cos 0text{textdegree}=1, sin 0text{textdegree}=0, \ cos 90text{textdegree}=0$ and $color{#4257b2}sin 90text{textdegree}=1$

We note that the value of $color{#4257b2}sin left(0text{textdegree}+90text{textdegree}right)$ does not equal the value of
$color{#4257b2}cos 0text{textdegree}cos 90text{textdegree}+sin 0text{textdegree}sin 90text{textdegree}$, so the equation $color{#4257b2}sin left(x+yright)=cos xcos y+sin xsin y$ is not an identity.

(d) We would like to use a counterexample to show that the equation $color{#4257b2}cos 2x=1+2sin^{2}x$ is not an identity. Since we need to prove that $color{#4257b2}cos 2x=1+2sin^{2}x$ is not an identity, we can substitute $color{#4257b2}x=45text{textdegree}$ and show if $color{#4257b2}cos 2x$ will equal $color{#4257b2}1+2sin^{2}x$ or not.

$$
cos 2x=1+2sin^{2}x
$$

$$
cos left(2cdot 45text{textdegree}right)=1+2sin^{2}45text{textdegree}
$$

$$
cos 90text{textdegree}=1+2left(dfrac{1}{sqrt{2}}right)^{2}
$$

$$
0=1+2cdot left(dfrac{1}{2}right)
$$

$$
0=1+1
$$

$$
0=2
$$

Note that the angles $color{#4257b2}45text{textdegree}$ and $color{#4257b2}90text{textdegree}$ are special angles which we know the values of the sine and cosine functions for it where $color{#4257b2}sin 45text{textdegree}=dfrac{1}{sqrt{2}}$ and $color{#4257b2}cos 90text{textdegree}=0$

We note that the value of $color{#4257b2}cos left(2cdot 45text{textdegree}right)$ does not equal the value of $color{#4257b2}1+2sin^{2}45text{textdegree}$, so the equation $color{#4257b2}cos 2x=1+2sin^{2}x$ is not an identity.

$color{#c34632}(a) cos x=dfrac{1}{cos x}{color{Black$ is not an identity}
\
\
$(b) 1-tan^{2}x=sec^{2}x$ {color{Black}is not an identity}}
\
\
Large$$text{color{#c34632}(c) left(sin x+cos xright)=cos xcos y+sin xsin y{color{Black$ is not an identity}
\
\
$(d) cos 2x=1+sin^{2}x$ {color{Black}is not an identity}}}$

We would like to graph the function $color{#4257b2}dfrac{1-tan^{2}x}{1+tan^{2}x}$. We can use the graphing calculator to graph it as follows:

We note from the graph that the function $color{#4257b2}dfrac{1-tan^{2}x}{1+tan^{2}x}$ has the same graph of the cosine function where the period is $color{#4257b2}pi$ which means that it has the same graph of the function $color{#4257b2}cos 2x$, so we can make a conjecture that the expression $color{#4257b2}dfrac{1-tan^{2}x}{1+tan^{2}x}$ is equivalent to the expression $color{#4257b2}cos 2x$

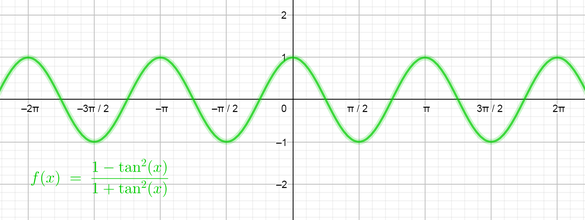
$$
color{#c34632}dfrac{1-tan^{2}x}{1+tan^{2}x}=cos 2x
$$

We would like to prove our conjecture in question $6$, so we need to prove that $color{#4257b2}dfrac{1-tan^{2}x}{1+tan^{2}x}=cos 2x$ is an identity as.

First, we can simplify the left side $color{#4257b2}dfrac{1-tan^{2}x}{1+tan^{2}x}$ where we know from the Pythagorean identity that $color{#4257b2}1+tan^{2}x=sec^{2}x$ and then simplify.

$$
begin{align*}
dfrac{1-tan^{2}x}{1+tan^{2}x}&=dfrac{1-tan^{2}x}{sec^{2}x}
\ \
&=dfrac{1-tan^{2}x}{dfrac{1}{cos^{2}x}}
\ \
&=cos^{2}xleft(1-tan^{2}xright)
\ \
&=cos^{2}x-cos^{2}xtan^{2}x
\ \
&=cos^{2}x-cos^{2}xcdot dfrac{sin^{2}x}{cos^{2}x}
\ \
&=cos^{2}x-cancel{cos^{2}x}cdot dfrac{sin^{2}x}{cancel{cos^{2}x}}
\ \
&=cos^{2}x-sin^{2}x
end{align*}
$$

Note that we know the identity $color{#4257b2}sec theta=dfrac{1}{cos theta}$, so we replaced $color{#4257b2}sec^{2}x$ by $color{#4257b2}dfrac{1}{cos^{2}x}$.

Now we simplified the left side $color{#4257b2}dfrac{1-tan^{2}x}{1+tan^{2}x}$ to the expression $color{#4257b2}cos^{2}x-sin^{2}x$ but we know from the double angle formula of the cosine function that $color{#4257b2}cos 2x=cos^{2}x-sin^{2}x$, so we can replace $color{#4257b2}cos^{2}x-sin^{2}x$ by $color{#4257b2}cos 2x$.

$$
begin{align*}
dfrac{1-tan^{2}x}{1+tan^{2}x}&=cos^{2}x-sin^{2}x
\ \
&=cos 2x
end{align*}
$$

So we proved that the left side equals $color{#4257b2}cos 2x$ which means that the left side is equivalent to the right side.

Large{$text{color{#c34632}$dfrac{1-tan^{2}x}{1+tan^{2}x}=cos 2x$}$

We would like to prove that $color{#4257b2}dfrac{1+tan x}{1+cot x}=dfrac{1-tan x}{cot x-1}$. First, we can simplify the left side and then simplify the right side and show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}dfrac{1+tan x}{1+cot x}$, so we can multiply the numerator and denominator by $color{#4257b2}1-tan x$ and simplify.

$$
begin{align*}
dfrac{1+tan x}{1+cot x}&=left(dfrac{1+tan x}{1+cot x}right)cdot left(dfrac{1-tan x}{1-tan x}right)
\ \
&=dfrac{1-tan^{2}x}{1+cot x-tan x-tan xcot x}
\ \
&=dfrac{1-tan^{2}x}{1+cot x-tan x-1}
\ \
&=dfrac{1-tan^{2}x}{cot x-tan x}
end{align*}
$$

Note that we know that $color{#4257b2}cot x=dfrac{1}{tan x}$, so $color{#4257b2}tan xcot x=tan xcdot dfrac{1}{tan x}=1$.

Now we simplified the left side to the expression $color{#4257b2}dfrac{1-tan^{2}x}{cot x-tan x}$, so the next step is to simplify the right side and show if it will equal the left side or not.

We note that the right side is $color{#4257b2}dfrac{1-tan x}{cot x-1}$, so we can multiply the numerator and denominator by $color{#4257b2}1+tan x$ and simplify.

$$
begin{align*}
dfrac{1-tan x}{cot x-1}&=left(dfrac{1-tan x}{cot x-1}right)cdot left(dfrac{1+tan x}{1+tan x}right)
\ \
&=dfrac{1-tan^{2}x}{cot x-1+tan xcot x-tan x}
\ \
&=dfrac{1-tan^{2}x}{cot x-1+1-tan x}
\ \
&=dfrac{1-tan^{2}x}{cot x-tan x}
end{align*}
$$

So we note that the right side is also simplified to the expression $color{#4257b2}dfrac{1-tan^{2}x}{cot x-tan x}$, so we proved that the left side is equivalent to the right side which means that $color{#4257b2}dfrac{1+tan x}{1+cot x}=dfrac{1-tan x}{cot x-1}$

$$
color{#c34632}dfrac{1+tan x}{1+cot x}=dfrac{1-tan x}{cot x-1}
$$

(a) We would like to prove that $color{#4257b2}dfrac{cos^{2}theta-sin^{2}theta}{cos^{2}theta+sin thetacos theta}=1-tan theta$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}dfrac{cos^{2}theta-sin^{2}theta}{cos^{2}theta+sin thetacos theta}$, so we can factor the numerator and denominator to simplify where the numerator on the form $color{#4257b2}a^{2}-b^{2}$ which can be factored to $color{#4257b2}(a-b)(a+b)$ and for the denominator we can take $color{#4257b2}cos theta$ as a common factor.

$$
begin{align*}
dfrac{cos^{2}theta-sin^{2}theta}{cos^{2}theta+sin thetacos theta}&=dfrac{left(cos theta-sin thetaright)left(cos theta+sin thetaright)}{cos thetaleft(cos theta+sin thetaright)}
\ \
&=dfrac{left(cos theta-sin thetaright)cancel{left(cos theta+sin thetaright)}}{cos thetacancel{left(cos theta+sin thetaright)}}
\ \
&=dfrac{cos theta-sin theta}{cos theta}
end{align*}
$$

Now we proved that the left side is simplified to $color{#4257b2}dfrac{cos theta-sin theta}{cos theta}$, so the next step is to split this fraction to two subtracted fractions where $color{#4257b2}dfrac{a-b}{c}=dfrac{a}{c}-dfrac{b}{c}$.

$$
begin{align*}
dfrac{cos^{2}theta-sin^{2}theta}{cos^{2}theta+sin thetacos theta}&=dfrac{cos theta-sin theta}{cos theta}
\ \
&=dfrac{cos theta}{cos theta}-dfrac{sin theta}{cos theta}
\ \
&=1-tan theta
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$.

So we proved that the left side can be simplified to $color{#4257b2}1-tan theta$ which means that the left side is equivalent to the right side.

(b) We would like to prove that $color{#4257b2}tan^{2}x-sin^{2}x=sin^{2}xtan^{2}x$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}tan^{2}x-sin^{2}x$, so we can use the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$ to replace $color{#4257b2}tan^{2}x$ by $color{#4257b2}dfrac{sin^{2}x}{cos^{2}x}$.

$$
tan^{2}x-sin^{2}x=dfrac{sin^{2}x}{cos^{2}x}-sin^{2}x
$$

Now we can unify the denominators using the common denominator $color{#4257b2}cos^{2}x$.

$$
begin{align*}
tan^{2}x-sin^{2}x&=dfrac{sin^{2}x}{cos^{2}x}-sin^{2}x
\ \
&=dfrac{sin^{2}x-sin^{2}xcos^{2}x}{cos^{2}x}
\ \
&=dfrac{sin^{2}xleft(1-cos^{2}xright)}{cos^{2}x}
end{align*}
$$

But we know from the Pythagorean identity that $color{#4257b2}sin^{2}theta+cos^{2}theta=1$, so $color{#4257b2}sin^{2}theta=1-cos^{2}theta$ and we can replace $color{#4257b2}1-cos^{2}x$ by $color{#4257b2}sin^{2}x$.

$$
begin{align*}
tan^{2}x-sin^{2}x&=dfrac{sin^{2}xleft(1-cos^{2}xright)}{cos^{2}x}
\ \
&=dfrac{sin^{2}xsin^{2}x}{cos^{2}x}
\ \
&=dfrac{sin^{2}x}{1}cdot dfrac{sin^{2}x}{cos^{2}x}
\ \
&=sin^{2}xtan^{2}x
end{align*}
$$

So we proved that the left side can be simplified to $color{#4257b2}sin^{2}xtan^{2}x$ which means that the left side is equivalent to the right side.

(c) We would like to prove that $color{#4257b2}tan^{2}x-cos^{2}x=dfrac{1}{cos^{2}x}-1-cos^{2}x$. First, we can simplify the right side to show if they are equivalent to each other or not.

We note that the right side is $color{#4257b2}dfrac{1}{cos^{2}x}-1-cos^{2}x$, so we can use the identity $color{#4257b2}sec theta=dfrac{1}{cos theta}$ to replace $color{#4257b2}dfrac{1}{cos^{2}x}$ by $color{#4257b2}sec^{2}x$.

$$
dfrac{1}{cos^{2}x}-1-cos^{2}x=sec^{2}x-1-cos^{2}x
$$

But we know from the Pythagorean identity that $color{#4257b2}1+tan^{2}theta=sec^{2}theta$, so $color{#4257b2}tan^{2}theta=sec^{2}theta-1$ and we can replace $color{#4257b2}sec^{2}x-1$ by $color{#4257b2}tan^{2}x$.

$$
begin{align*}
dfrac{1}{cos^{2}x}-1-cos^{2}x&=sec^{2}x-1-cos^{2}x
\ \
&=left(sec^{2}x-1right)-cos^{2}x
\ \
&=tan^{2}x-cos^{2}x
end{align*}
$$

So we proved that the right side can be simplified to $color{#4257b2}tan^{2}x-cos^{2}x$ which means that the left side is equivalent to the right side.

(d) We would like to prove that $color{#4257b2}dfrac{1}{1+cos theta}+dfrac{1}{1-cos theta}=dfrac{2}{sin^{2}x}$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}dfrac{1}{1+cos theta}+dfrac{1}{1-cos theta}$, so we can unify the denominators using the common denominator $color{#4257b2}left(1+cos thetaright)left(1-cos thetaright)$.

$$
begin{align*}
dfrac{1}{1+cos theta}+dfrac{1}{1-cos theta}&=dfrac{1cdot left(1-cos thetaright)+1cdot left(1+cos thetaright)}{left(1+cos thetaright)left(1-cos thetaright)}
\ \
&=dfrac{1-cos theta+1+cos theta}{1^{2}-cos^{2}theta}
\ \
&=dfrac{1cancel{-cos theta}+1+cancel{cos theta}}{1-cos^{2}theta}
\ \
&=dfrac{2}{1-cos^{2}theta}
end{align*}
$$

But we know from the Pythagorean identity that $color{#4257b2}sin^{2}theta+cos^{2}theta=1$, so $color{#4257b2}sin^{2}theta=1-cos^{2}theta$ and we can replace $color{#4257b2}1-cos^{2}theta$ by $color{#4257b2}sin^{2}theta$.

$$
begin{align*}
dfrac{1}{1+cos theta}+dfrac{1}{1-cos theta}&=dfrac{2}{1-cos^{2}theta}
\ \
&=dfrac{2}{sin^{2}theta}
end{align*}
$$

So we proved that the left side can be simplified to $color{#4257b2}dfrac{2}{sin^{2}theta}$ which means that the left side is equivalent to the right side.

$$
text{color{#c34632}$(a) dfrac{cos^{2}theta-sin^{2}theta}{cos^{2}theta+sin thetacos theta}=1-tan theta$
\
\
\
$(b) tan^{2}x-sin^{2}x=sin^{2}xtan^{2}x$
\
\
\
$(c) tan^{2}x-cos^{2}x=dfrac{1}{cos^{2}x}-1-cos^{2}x$
\
\
\
$(d) dfrac{1}{1+cos theta}+dfrac{1}{1-cos theta}=dfrac{2}{sin^{2}theta}$}
$$

(a) We would like to prove that $color{#4257b2}cos xtan^{3}x=sin xtan^{2}x$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}cos xtan^{3}x$, so we can split $color{#4257b2}tan^{3}x$ to $color{#4257b2}tan xtan^{2}x$ and then use the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$ to replace $color{#4257b2}tan x$ by $color{#4257b2}dfrac{sin x}{cos x}$.

$$
begin{align*}
cos xtan^{3}x&=cos xtan xtan^{2}x
\ \
&=cos xleft(dfrac{sin x}{cos x}right)tan^{2}x
\ \
&=cancel{cos x}left(dfrac{sin x}{cancel{cos x}}right)tan^{2}x
\ \
&=sin xtan^{2}x
end{align*}
$$

So we proved that the left side can be simplified to $color{#4257b2}sin xtan^{2}x$ which means that the left side is equivalent to the right side.

(b) We would like to prove that $color{#4257b2}sin^{2}theta+cos^{4}theta=cos^{2}theta+sin^{4}theta$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}sin^{2}theta+cos^{4}theta$, so we can say that
$color{#4257b2}cos^{4}theta=left(cos^{2}thetaright)^{2}$. But we know from the Pythagorean identity that
$color{#4257b2}sin^{2}theta+cos^{2}theta=1$, so $color{#4257b2}cos^{2}theta=1-sin^{2}theta$ and we can use this identity to simplify the left side.

$$
begin{align*}
sin^{2}theta+cos^{4}theta&=sin^{2}theta+left(cos^{2}thetaright)^{2}
\ \
&=sin^{2}theta+left(1-sin^{2}thetaright)^{2}
end{align*}
$$

Now we can distribute the exponent where we know that
$color{#4257b2}(a-b)^{2}=a^{2}-2ab+b^{2}$.

$$
begin{align*}
sin^{2}theta+cos^{4}theta&=sin^{2}theta+left(1-sin^{2}thetaright)^{2}
\ \
&=sin^{2}theta+1-2sin^{2}theta+sin^{4}theta
\ \
&=1-sin^{2}theta+sin^{4}theta
end{align*}
$$

Now we can use the Pythagorean identity again but this time to replace $color{#4257b2}1-sin^{2}theta$ by $color{#4257b2}cos^{2}theta$

$$
begin{align*}
sin^{2}theta+cos^{4}theta&=1-sin^{2}theta+sin^{4}theta
\ \
&=cos^{2}theta+sin^{4}theta
end{align*}
$$

So we proved that the left side can be simplified to $color{#4257b2}cos^{2}theta+sin^{4}theta$ which means that the left side is equivalent to the right side.

(c) We would like to prove that $color{#4257b2}left(sin x+cos xright)left(dfrac{tan^{2}x+1}{tan x}right)=dfrac{1}{cos x}+dfrac{1}{sin x}$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}left(sin x+cos xright)left(dfrac{tan^{2}x+1}{tan x}right)$, so we can use the Pythagorean identity $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ to replace $color{#4257b2}tan^{2}x+1$ by $color{#4257b2}sec^{2}x$.

$$
begin{align*}
left(sin x+cos xright)left(dfrac{tan^{2}x+1}{tan x}right)&=left(sin x+cos xright)left(dfrac{sec^{2}x}{tan x}right)
\ \
&=left(sin x+cos xright)left(dfrac{dfrac{1}{cos^{2}x}}{tan x}right)
\ \
&=left(sin x+cos xright)left(dfrac{1}{tan xcos^{2}x}right)
\ \
&=left(sin x+cos xright)left(dfrac{1}{dfrac{sin x}{cos x}cdot cos^{2}x}right)
\ \
&=left(sin x+cos xright)left(dfrac{1}{dfrac{sin x}{cancel{cos x}}cdot cos^{cancel{2}}x}right)
\ \
&=left(sin x+cos xright)left(dfrac{1}{sin xcos x}right)
\ \
&=dfrac{sin x+cos x}{sin xcos x}
end{align*}
$$

Note that we used the identities $color{#4257b2}sec x=dfrac{1}{cos x}$ and $color{#4257b2}tan x=dfrac{sin x}{cos x}$ to simplify. Now the final step is to split the fraction to two fractions where
$color{#4257b2}dfrac{a+b}{c}=dfrac{a}{c}+dfrac{b}{c}$.

$$
begin{align*}
left(sin x+cos xright)left(dfrac{tan^{2}x+1}{tan x}right)&=dfrac{sin x+cos x}{sin xcos x}
\ \
&=dfrac{sin x}{sin xcos x}+dfrac{cos x}{sin xcos x}
\ \
&=dfrac{cancel{sin x}}{cancel{sin x}cos x}+dfrac{cancel{cos x}}{sin xcancel{cos x}}
\ \
&=dfrac{1}{cos x}+dfrac{1}{sin x}
end{align*}
$$

So we proved that the left side can be simplified to $color{#4257b2}dfrac{1}{cos x}+dfrac{1}{sin x}$ which means that the left side is equivalent to the right side.

(d) We would like to prove that $color{#4257b2}tan^{2}beta+cos^{2}beta+sin^{2}beta=dfrac{1}{cos^{2}beta}$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}tan^{2}beta+cos^{2}beta+sin^{2}beta$, so we can use the Pythagorean identity $color{#4257b2}sin^{2}theta+cos^{2}theta=1$ to replace $color{#4257b2}cos^{2}beta+sin^{2}beta$ by $color{#4257b2}1$.

$$
tan^{2}beta+cos^{2}beta+sin^{2}beta=tan^{2}beta+1
$$

Now we can use the Pythagorean identity $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ to replace $color{#4257b2}tan^{2}beta+1$ by $color{#4257b2}sec^{2}beta$.

$$
begin{align*}
tan^{2}beta+cos^{2}beta+sin^{2}beta&=tan^{2}beta+1
\ \
&=sec^{2}beta
\ \
&=dfrac{1}{cos^{2}beta}
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}sec theta=dfrac{1}{cos theta}$ to replace $color{#4257b2}sec^{2}beta$ by $color{#4257b2}dfrac{1}{cos^{2}beta}$.

So we proved that the left side can be simplified to $color{#4257b2}dfrac{1}{cos^{2}beta}$ which means that the left side is equivalent to the right side.

(e) We would like to prove that $color{#4257b2}sin left(dfrac{pi}{4}+xright)+sin left(dfrac{pi}{4}-xright)=sqrt{2} cos x$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side $color{#4257b2}sin left(dfrac{pi}{4}+xright)+sin left(dfrac{pi}{4}-xright)$ consists of two sine functions each of them contains compound angle, so we can use addition and subtraction formula for the sine function $color{#4257b2}sin(a+b)=sin acos b+cos asin b$ and $color{#4257b2}sin(a-b)=sin acos b-cos asin b$.

$$
begin{align*}
sin left(dfrac{pi}{4}+xright)+sin left(dfrac{pi}{4}-xright)&=sin dfrac{pi}{4}cos x+cos dfrac{pi}{4}sin x+sin dfrac{pi}{4}cos x-cos dfrac{pi}{4}sin x
\ \
&=sin dfrac{pi}{4}cos x+cancel{cos dfrac{pi}{4}sin x}+sin dfrac{pi}{4}cos xcancel{-cos dfrac{pi}{4}sin x}
\ \
&=sin dfrac{pi}{4}cos x+sin dfrac{pi}{4}cos x
\ \
&=2sin dfrac{pi}{4}cos x
\ \
&=2cdot dfrac{sqrt{2}}{2} cos x
\ \
&=sqrt{2} cos x
end{align*}
$$

Note that the angle $color{#4257b2}dfrac{pi}{4}$ is a special angle which we know the value of the sine function for it where $color{#4257b2}sin dfrac{pi}{4}=dfrac{sqrt{2}}{2}$.

So we proved that the left side can be simplified to $color{#4257b2}sqrt{2} cos x$ which means that the left side is equivalent to the right side.

(f) We would like to prove that $color{#4257b2}sin left(dfrac{pi}{2}-xright)cot left(dfrac{pi}{2}+xright)=-sin x$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}sin left(dfrac{pi}{2}-xright)cot left(dfrac{pi}{2}+xright)$, so we can use the identity $color{#4257b2}cot theta=dfrac{cos theta}{sin theta}$ to replace $color{#4257b2}cot left(dfrac{pi}{2}+xright)$ by $color{#4257b2}dfrac{cos left(dfrac{pi}{2}+xright)}{sin left(dfrac{pi}{2}+xright)}$.

$$
begin{align*}
sin left(dfrac{pi}{2}-xright)cot left(dfrac{pi}{2}+xright)&=sin left(dfrac{pi}{2}-xright)cdot dfrac{cos left(dfrac{pi}{2}+xright)}{sin left(dfrac{pi}{2}+xright)}
\ \
&=dfrac{sin left(dfrac{pi}{2}-xright)cos left(dfrac{pi}{2}+xright)}{sin left(dfrac{pi}{2}+xright)}
end{align*}
$$

But we know from the transformation that $color{#4257b2}sin left(dfrac{pi}{2}-xright)=cos x, \ sin left(dfrac{pi}{2}+xright)=cos x$ and also $color{#4257b2}cos left(dfrac{pi}{2}+xright)=-sin x$, so we can use these formulas to simplify the left side.

$$
begin{align*}
sin left(dfrac{pi}{2}-xright)cot left(dfrac{pi}{2}+xright)&=dfrac{sin left(dfrac{pi}{2}-xright)cos left(dfrac{pi}{2}+xright)}{sin left(dfrac{pi}{2}+xright)}
\ \
&=dfrac{cos xcdot left(-sin xright)}{cos x}
\ \
&=dfrac{cancel{cos x}cdot left(-sin xright)}{cancel{cos x}}
\ \
&=-sin x
end{align*}
$$

So we proved that the left side can be simplified to $color{#4257b2}-sin x$ which means that the left side is equivalent to the right side.

$$
text{color{#c34632}$(a) cos xtan^{3}x=sin xtan^{2}x$
\
\
\
$(b) sin^{2}theta+cos^{4}theta=cos^{2}theta+sin^{4}theta$
\
\
\
$(c) left(sin x+cos xright)left(dfrac{tan^{2}x+1}{tan x}right)=dfrac{1}{cos x}+dfrac{1}{sin x}$
\
\
\
$(d) tan^{2}beta+cos^{2}beta+sin^{2}beta=dfrac{1}{cos^{2}beta}$
\
\
\
$(e) sin left(dfrac{pi}{4}+xright)+sin left(dfrac{pi}{4}-xright)=sqrt{2} cos x$
\
\
\
$(f) sin left(dfrac{pi}{2}-xright)cot left(dfrac{pi}{2}+xright)=-sin x$}
$$

(a) We would like to prove that $color{#4257b2}dfrac{cos 2x+1}{sin 2x}=cot x$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side $color{#4257b2}dfrac{cos 2x+1}{sin 2x}$ consists of a cosine function in the numerator and a sine function in the denominator each of them contains double angle of $color{#4257b2}x$, so we can use the double angle formulas for the sine and cosine functions $color{#4257b2}sin 2x=2sin xcos x$ and $color{#4257b2}cos 2x=2cos^{2}x-1$.

$$
begin{align*}
dfrac{cos 2x+1}{sin 2x}&=dfrac{2cos^{2}x-1+1}{2sin xcos x}
\ \
&=dfrac{2cos^{2}xcancel{-1}+cancel{1}}{2sin xcos x}
\ \
&=dfrac{2cos^{2}x}{2sin xcos x}
\ \
&=dfrac{cancel{2}cos^{cancel{2}}x}{cancel{2}sin xcancel{cos x}}
\ \
&=dfrac{cos x}{sin x}
\ \
&=cot x
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}cot x=dfrac{cos x}{sin x}$.

So we proved that the left side can be simplified to $color{#4257b2}cot x$ which means that the left side is equivalent to the right side.

(b) We would like to prove that $color{#4257b2}dfrac{sin 2x}{1-cos 2x}=cot x$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side $color{#4257b2}dfrac{sin 2x}{1-cos 2x}$ consists of a sine function in the numerator and a cosine function in the denominator each of them contains double angle of $color{#4257b2}x$, so we can use the double angle formulas for the sine and cosine functions $color{#4257b2}sin 2x=2sin xcos x$ and $color{#4257b2}cos 2x=1-2sin^{2}x$.

$$
begin{align*}
dfrac{sin 2x}{1-cos 2x}&=dfrac{2sin xcos x}{1-left(1-2sin^{2}xright)}
\ \
&=dfrac{2sin xcos x}{1-1+2sin^{2}x}
\ \
&=dfrac{2sin xcos x}{cancel{1}cancel{-1}+2sin^{2}x}
\ \
&=dfrac{2sin xcos x}{2sin^{2}x}
\ \
&=dfrac{cancel{2sin x}cos x}{cancel{2}sin^{cancel{2}}x}
\ \
&=dfrac{cos x}{sin x}
\ \
&=cot x
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}cot x=dfrac{cos x}{sin x}$.

So we proved that the left side can be simplified to $color{#4257b2}cot x$ which means that the left side is equivalent to the right side.

(c) We would like to prove that $color{#4257b2}left(sin x+cos xright)^{2}=1+sin 2x$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}left(sin x+cos xright)^{2}$, so we can distribute the exponent where $color{#4257b2}left(a+bright)^{2}=a^{2}+2ab+b^{2}$.

$$
begin{align*}
left(sin x+cos xright)^{2}&=sin^{2}x+2sin xcos x+cos^{2}x
\ \
&=left(sin^{2}x+cos^{2}xright)+2sin xcos x
end{align*}
$$

But we know from the Pythagorean identity that $color{#4257b2}sin^{2}x+cos^{2}x=1$, so we can use this identity to simplify the left side.

$$
begin{align*}
left(sin x+cos xright)^{2}&=left(sin^{2}x+cos^{2}xright)+2sin xcos x
\ \
&=1+2sin xcos x
end{align*}
$$

Now we simplified the left side to the expression $color{#4257b2}1+2sin xcos x$, so the next step is to use the double angle formula for the sine function where $color{#4257b2}sin 2x=2sin xcos x$.

$$
begin{align*}
left(sin x+cos xright)^{2}&=1+2sin xcos x
\ \
&=1+sin 2x
end{align*}
$$

So we proved that the left side can be simplified to $color{#4257b2}1+sin 2x$ which means that the left side is equivalent to the right side.

(d) We would like to prove that $color{#4257b2}cos^{4}theta-sin^{4}theta=cos 2theta$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}cos^{4}theta-sin^{4}theta$, so we can factor where
$color{#4257b2}a^{4}-b^{4}=left(a^{2}+b^{2}right)left(a^{2}-b^{2}right)$.

$$
begin{align*}
cos^{4}theta-sin^{4}theta&=left(cos^{2}theta+sin^{2}thetaright)left(cos^{2}theta-sin^{2}thetaright)
end{align*}
$$

But we know from the Pythagorean identity that $color{#4257b2}sin^{2}theta+cos^{2}theta=1$, so we can use this identity to simplify the left side.

$$
begin{align*}
cos^{4}theta-sin^{4}theta&=left(cos^{2}theta+sin^{2}thetaright)left(cos^{2}theta-sin^{2}thetaright)
\ \
&=1cdot left(cos^{2}theta-sin^{2}thetaright)
\ \
&=cos^{2}theta-sin^{2}theta
end{align*}
$$

Now we simplified the left side to the expression $color{#4257b2}cos^{2}theta-sin^{2}theta$, so the next step is to use the double angle formula for the cosine function where
$color{#4257b2}cos 2theta=cos^{2}theta-sin^{2}theta$.

$$
begin{align*}
cos^{4}theta-sin^{4}theta&=cos^{2}theta-sin^{2}theta
\ \
&=cos 2theta
end{align*}
$$

So we proved that the left side can be simplified to $color{#4257b2}cos 2theta$ which means that the left side is equivalent to the right side.

(e) We would like to prove that $color{#4257b2}cot theta-tan theta=2cot 2theta$. First, we can simplify the right side to show if they are equivalent to each other or not.

We note that the right side is $color{#4257b2}2cot 2theta$, so we can use the identity $color{#4257b2}cot theta=dfrac{1}{tan theta}$ to replace $color{#4257b2}cot 2theta$ by $color{#4257b2}dfrac{1}{tan 2theta}$.

$$
2cot 2theta=dfrac{2}{tan 2theta}
$$

Now we note that the right side contains the tangent function with a double angle of $color{#4257b2}theta$, so we can use the double angle formula for the tangent function where $color{#4257b2}tan 2theta=dfrac{2tan theta}{1-tan^{2}theta}$

$$
begin{align*}
2cot 2theta&=dfrac{2}{tan 2theta}
\ \
&=dfrac{2}{dfrac{2tan theta}{1-tan^{2}theta}}
\ \
&=dfrac{2left(1-tan^{2}thetaright)}{2tan theta}
\ \
&=dfrac{cancel{2}left(1-tan^{2}thetaright)}{cancel{2}tan theta}
\ \
&=dfrac{1-tan^{2}theta}{tan theta}
\ \
&=dfrac{1}{tan theta}-dfrac{tan^{2}theta}{tan theta}
\ \
&=cot theta-tan theta
end{align*}
$$

So we proved that the right side can be simplified to $color{#4257b2}cot theta-tan theta$ which means that the left side is equivalent to the right side.

(f) We would like to prove that $color{#4257b2}cot theta+tan theta=2csc 2theta$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side is $color{#4257b2}cot theta+tan theta$, so we can use the identity $color{#4257b2}cot theta=dfrac{1}{tan theta}$.

$$
cot theta+tan theta=dfrac{1}{tan theta}+tan theta
$$

Now we can unify the denominators with the common denominator $color{#4257b2}tan theta$.

$$
begin{align*}
cot theta+tan theta&=dfrac{1}{tan theta}+tan theta
\ \
&=dfrac{1+tan thetatan theta}{tan theta}
\ \
&=dfrac{1+tan^{2}theta}{tan theta}
end{align*}
$$

But we know from the Pythagorean identity that $color{#4257b2}1+tan^{2}theta=sec^{2}theta$, so we can use this identity to simplify the left side.

$$
begin{align*}
cot theta+tan theta&=dfrac{1+tan^{2}theta}{tan theta}
\ \
&=dfrac{sec^{2}theta}{tan theta}
\ \
&=dfrac{dfrac{1}{cos^{2}theta}}{tan theta}
\ \
&=dfrac{1}{tan thetacos^{2}theta}
end{align*}
$$

Note that we used the identity $color{#4257b2}sec theta=dfrac{1}{cos theta}$ to replace $color{#4257b2}sec^{2}theta$ by $color{#4257b2}dfrac{1}{cos^{2}theta}$, Now the next step is to use the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$

$$
begin{align*}
cot theta+tan theta&=dfrac{1}{tan thetacos^{2}theta}
\ \
&=dfrac{1}{dfrac{sin theta}{cos theta}cdot cos^{2}theta}
\ \
&=dfrac{1}{dfrac{sin theta}{cancel{cos theta}}cdot cos^{cancel{2}}theta}
\ \
&=dfrac{1}{sin thetacos theta}
\ \
&=dfrac{2}{2sin thetacos theta}
end{align*}
$$

Now we simplified the left side to the expression $color{#4257b2}dfrac{2}{2sin thetacos theta}$, so the next step is to use the double angle formula for the sine function where
$color{#4257b2}sin 2theta=2sin thetacos theta$.

$$
begin{align*}
cot theta+tan theta&=dfrac{2}{2sin thetacos theta}
\ \
&=dfrac{2}{sin 2theta}
\ \
&=2csc 2theta
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}csc theta=dfrac{1}{sin theta}$ to replace $color{#4257b2}dfrac{1}{sin 2theta}$ by $color{#4257b2}csc 2theta$.

So we proved that the left side can be simplified to $color{#4257b2}2csc 2theta$ which means that the left side is equivalent to the right side.

(g) We would like to prove that $color{#4257b2}dfrac{1+tan x}{1-tan x}=tan left(x+dfrac{pi}{4}right)$. First, we can simplify the right side to show if they are equivalent to each other or not.

We note that the right side $color{#4257b2}tan left(x+dfrac{pi}{4}right)$ consists of a tangent function which contains a compound angle, so we can use the addition formula for the tangent function $color{#4257b2}tan (a+b)=dfrac{tan a+tan b}{1-tan atan b}$.

$$
begin{align*}
tan left(x+dfrac{pi}{4}right)&=dfrac{tan x+tan dfrac{pi}{4}}{1-tan xtan dfrac{pi}{4}}
\ \
&=dfrac{tan x+1}{1-tan xcdot (1)}
\ \
&=dfrac{tan x+1}{1-tan x}
\ \
&=dfrac{1+tan x}{1-tan x}
end{align*}
$$

Note that the angle $color{#4257b2}dfrac{pi}{4}$ is a special angle which we know the value of the tangent function of it where $color{#4257b2}tan dfrac{pi}{4}=1$.

So we proved that the right side can be simplified to $color{#4257b2}dfrac{1+tan x}{1-tan x}$ which means that the left side is equivalent to the right side.

(h) We would like to prove that $color{#4257b2}csc 2x+cot 2x=cot x$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side $color{#4257b2}csc 2x+cot 2x$, so we can use the identities $color{#4257b2}csc theta=dfrac{1}{sin theta}$ and $color{#4257b2}cot theta=dfrac{cos theta}{sin theta}$ to replace $color{#4257b2}csc 2x$ and $color{#4257b2}cot 2x$ by $color{#4257b2}dfrac{1}{sin 2x}$ and $color{#4257b2}dfrac{cos 2x}{sin 2x}$.

$$
begin{align*}
csc 2x+cot 2x&=dfrac{1}{sin 2x}+dfrac{cos 2x}{sin 2x}
\ \
&=dfrac{1+cos 2x}{sin 2x}
end{align*}
$$

Now we note that the left side is simplified to $color{#4257b2}dfrac{1+cos 2x}{sin 2x}$, so we can use the double angle formulas for the sine and cosine functions where
$color{#4257b2}sin 2x=2sin x cos x$ and $color{#4257b2}cos 2x=2cos^{2}x-1$.

$$
begin{align*}
csc 2x+cot 2x&=dfrac{1+cos 2x}{sin 2x}
\ \
&=dfrac{1+2cos^{2}x-1}{2sin xcos x}
\ \
&=dfrac{cancel{1}+2cos^{2}xcancel{-1}}{2sin xcos x}
\ \
&=dfrac{2cos^{2}x}{2sin xcos x}
\ \
&=dfrac{cancel{2}cos^{cancel{2}}x}{cancel{2}sin xcancel{cos x}}
\ \
&=dfrac{cos x}{sin x}=cot x
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}cot x=dfrac{cos x}{sin x}$.

So we proved that the left side can be simplified to $color{#4257b2}cot x$ which means that the left side is equivalent to the right side.

(i) We would like to prove that $color{#4257b2}dfrac{2tan x}{1+tan^{2}x}=sin 2x$. First, we can simplify the left side to show if they are equivalent to each other or not.

We note that the left side $color{#4257b2}dfrac{2tan x}{1+tan^{2}x}$, so we can use the Pythagorean identity $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ to replace $color{#4257b2}1+tan^{2}x$ by $color{#4257b2}sec^{2}x$.

$$
begin{align*}
dfrac{2tan x}{1+tan^{2}x}&=dfrac{2tan x}{sec^{2}x}
\ \
&=dfrac{2tan x}{dfrac{1}{cos^{2}x}}
\ \
&=cos^{2}xleft(2tan xright)
\ \
&=2tan xcos^{2}x
end{align*}
$$

Note that we used the identity $color{#4257b2}sec theta=dfrac{1}{cos theta}$ to replace $color{#4257b2}sec^{2}x$ by $color{#4257b2}dfrac{1}{cos^{2}x}$. Now we can use the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$ to simplify the left side.

$$
begin{align*}
dfrac{2tan x}{1+tan^{2}x}&=2tan xcos^{2}x
\ \
&=2left(dfrac{sin x}{cos x}right)cos^{2}x
\ \
&=2left(dfrac{sin x}{cancel{cos x}}right)cos^{cancel{2}}x
\ \
&=2sin xcos x=sin 2x
end{align*}
$$

Note that in the final step we used the double angle formula for the sine function where $color{#4257b2}sin 2x=2sin xcos x$.

So we proved that the left side can be simplified to $color{#4257b2}sin 2x$ which means that the left side is equivalent to the right side.

(j) We would like to prove that $color{#4257b2}sec 2t=dfrac{csc t}{csc t-2sin t}$. First, we can simplify the right side to show if they are equivalent to each other or not.

We note that the right side is $color{#4257b2}dfrac{csc t}{csc t-2sin t}$, so we can multiply the numerator and denominator by $color{#4257b2}sin t$.

$$
begin{align*}
dfrac{csc t}{csc t-2sin t}&=dfrac{sin tcsc t}{sin tleft(csc t-2sin tright)}
\ \
&=dfrac{sin tcsc t}{sin tcsc t-2sin tsin t}
\ \
&=dfrac{sin tcsc t}{sin tcsc t-2sin^{2}t}
end{align*}
$$

Now we can use the identity $color{#4257b2}csc theta=dfrac{1}{sin theta}$ to replace $color{#4257b2}csc t$ by $color{#4257b2}dfrac{1}{sin t}$.

$$
begin{align*}
dfrac{csc t}{csc t-2sin t}&=dfrac{sin tcsc t}{sin tcsc t-2sin^{2}t}
\ \
&=dfrac{sin tcdot left(dfrac{1}{sin t}right)}{sin tcdot left(dfrac{1}{sin t}right)-2sin^{2}t}
\ \
&=dfrac{cancel{sin t}cdot left(dfrac{1}{cancel{sin t}}right)}{cancel{sin t}cdot left(dfrac{1}{cancel{sin t}}right)-2sin^{2}t}
\ \
&=dfrac{1}{1-2sin^{2}t}
end{align*}
$$

Now we simplified the right side to the expression $color{#4257b2}dfrac{1}{1-2sin^{2}t}$, so the next step is to use the double angle formula for the cosine function where

$$
color{#4257b2}cos 2t=1-2sin^{2}t
$$

$$
begin{align*}
dfrac{csc t}{csc t-2sin t}&=dfrac{1}{1-2sin^{2}t}
\ \
&=dfrac{1}{cos 2t}
\ \
&=sec 2t
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}sec theta=dfrac{1}{cos theta}$ to replace $color{#4257b2}dfrac{1}{cos 2t}$ by $color{#4257b2}sec 2t$.

So we proved that the right side can be simplified to $color{#4257b2}sec 2t$ which means that the left side is equivalent to the right side.

(k) We would like to prove that $color{#4257b2}csc 2theta=dfrac{1}{2} left(sec thetaright)left(csc thetaright)$. First, we can simplify the right side to show if they are equivalent to each other or not.

We note that the right side $color{#4257b2}dfrac{1}{2} left(sec thetaright)left(csc thetaright)$, so we can use the identities
$color{#4257b2}sec theta=dfrac{1}{cos theta}$ and $color{#4257b2}csc theta=dfrac{1}{sin theta}$ to simplify the right side.

$$
begin{align*}
dfrac{1}{2} left(sec thetaright)left(csc thetaright)&=dfrac{1}{2} left(dfrac{1}{cos theta}right)left(dfrac{1}{sin theta}right)
\ \
&=dfrac{1}{2sin thetacos theta}
end{align*}
$$

Now we note that the right side is simplified to $color{#4257b2}dfrac{1}{2sin thetacos theta}$, so we can use the double angle formula for the sine function where $color{#4257b2}sin 2theta=2sin thetacos theta$.

$$
begin{align*}
dfrac{1}{2} left(sec thetaright)left(csc thetaright)&=dfrac{1}{2sin thetacos theta}
\ \
&=dfrac{1}{sin 2theta}
\ \
&=csc 2theta
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}csc theta=dfrac{1}{sin x}$ to replace $color{#4257b2}dfrac{1}{sin 2theta}$ by $color{#4257b2}csc 2theta$.

So we proved that the right side can be simplified to $color{#4257b2}2csc 2theta$ which means that the left side is equivalent to the right side.

(l) We would like to prove that $color{#4257b2}sec t=dfrac{sin 2t}{sin t}-dfrac{cos 2t}{cos t}$. First, we can simplify the right side to show if they are equivalent to each other or not.

We note that the right side $color{#4257b2}dfrac{sin 2t}{sin t}-dfrac{cos 2t}{cos t}$ consists of sine and cosine functions in the numerator each of them contains double angle of $color{#4257b2}t$, so we can use the double angle formulas for the sine and cosine functions $color{#4257b2}sin 2t=2sin tcos t$ and $color{#4257b2}cos 2t=2cos^{2}t-1$.

$$
begin{align*}
dfrac{sin 2t}{sin t}-dfrac{cos 2t}{cos t}&=dfrac{2sin tcos t}{sin t}-dfrac{2cos^{2}t-1}{cos t}
\ \
&=dfrac{2cancel{sin t}cos t}{cancel{sin t}}-left(dfrac{2cos^{2}t}{cos t}-dfrac{1}{cos t}right)
\ \
&=2cos t-left(dfrac{2cos^{cancel{2}}t}{cancel{cos t}}-dfrac{1}{cos t}right)
\ \
&=2cos t-left(2cos t-sec tright)
\ \
&=2cos t-2cos t+sec t
\ \
&=cancel{2cos t}cancel{-2cos t}+sec t
\ \
&=sec t
end{align*}
$$

Note that in the fourth step we used the identity $color{#4257b2}sec t=dfrac{1}{cos t}$.

So we proved that the right side can be simplified to $color{#4257b2}sec t$ which means that the left side is equivalent to the right side.

$$
text{color{#c34632}$(a) dfrac{cos 2x+1}{sin 2x}=cot x$ $(g) dfrac{1+tan x}{1-tan x}=tan left(x+dfrac{pi}{4}right)$
\
\
\
$(b) dfrac{sin 2x}{1-cos 2x}=cot x$ $(h) csc 2x+cot 2x=cot x$
\
\
\
$(c) left(sin x+cos xright)^{2}=1+sin 2x$ $(i) dfrac{2tan x}{1+tan^{2}x}=sin 2x$
\
\
\
$(d) cos^{4}theta-sin^{4}theta=cos 2theta$ $(j) sec 2t=dfrac{csc t}{csc t-2sin t}$
\
\
\
$(e) cot theta-tan theta=2cot 2theta$ $(k) csc 2theta=dfrac{1}{2} left(sec thetaright)left(csc thetaright)$
\
\
\
$(f) cot theta+tan theta=2csc 2theta$ $(l) sec t=dfrac{sin 2t}{sin t}-dfrac{cos 2t}{cos t}$}
$$

We would like to graph the function $color{#4257b2}dfrac{sin x+sin 2x}{1+cos x+cos 2x}$. We can use the graphing calculator to graph it as follows:

We note from the graph that the function $color{#4257b2}dfrac{sin x+sin 2x}{1+cos x+cos 2x}$ has the same graph of the tangent function where the period is $color{#4257b2}pi$ which means that it has the same graph of the function $color{#4257b2}tan x$, so we can make a conjecture that the expression $color{#4257b2}dfrac{sin x+sin 2x}{1+cos x+cos 2x}$ is equivalent to the expression $color{#4257b2}tan x$

$$
color{#c34632}dfrac{sin x+sin 2x}{1+cos x+cos 2x}=tan x
$$

We would like to prove our conjecture in question $12$, so we need to prove that $color{#4257b2}dfrac{sin x+sin 2x}{1+cos x+cos 2x}=tan x$ is an identity as.

First, we can simplify the left side $color{#4257b2}dfrac{sin x+sin 2x}{1+cos x+cos 2x}$ using the double angle formulas fro the sine and cosine functions where $color{#4257b2}sin 2x=2sin xcos x$ and $color{#4257b2}cos 2x=2cos^{2}x-1$.

$$
begin{align*}
dfrac{sin x+sin 2x}{1+cos x+cos 2x}&=dfrac{sin x+2sin xcos x}{1+cos x+2cos^{2}x-1}
\ \
&=dfrac{sin x+2sin xcos x}{cancel{1}+cos x+2cos^{2}xcancel{-1}}
\ \
&=dfrac{sin x+2sin xcos x}{cos x+2cos^{2}x}
end{align*}
$$

Now we can take $color{#4257b2}sin x$ as a common factor from the numerator and also we can take $color{#4257b2}cos x$ as a common factor from the denominator to simplify.

$$
begin{align*}
dfrac{sin x+sin 2x}{1+cos x+cos 2x}&=dfrac{sin x+2sin xcos x}{cos x+2cos^{2}x}
\ \
&=dfrac{sin xleft(1+2cos xright)}{cos xleft(1+2cos xright)}
\ \
&=dfrac{sin xcancel{left(1+2cos xright)}}{cos xcancel{left(1+2cos xright)}}
\ \
&=dfrac{sin x}{cos x}
\ \
&=tan x
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$ to replace $color{#4257b2}dfrac{sin x}{cos x}$ by $color{#4257b2}tan x$.

So we proved that the left side equals $color{#4257b2}tan x$ which means that the left side is equivalent to the right side.

Large{$text{color{#c34632}$dfrac{sin x+sin 2x}{1+cos x+cos 2x}=tan x$}$

We would like to know if $color{#4257b2}2sin xcos x=cos 2x$ is an identity or not. First, to know if the equations is an identity or not we need to simplify one side and show if its equivalent to the other side or not, if they are equivalent to each other, then the equations is an identity and if they are not equivalent to each other, then the equation is not an identity. So we can simplify the left side in the equation to show if it is equivalent to the right side or not.

We note that the left side is $color{#4257b2}2sin xcos x$ which is on the same form of the double angle formula for the sine function where $color{#4257b2}sin 2x=2sin xcos x$, so we can replace $color{#4257b2}2sin xcos x$ from the left side by $color{#4257b2}sin 2x$

$$
begin{align*}
text{The left side}&=2sin xcos x
\ \
&=sin 2x
end{align*}
$$

So we proved that the left side is equivalent to the expression $color{#4257b2}sin 2x$ not $color{#4257b2}cos 2x$, so the equation $color{#4257b2}2sin xcos x=cos 2x$ is not an identity.

Now we need to make the equation is an identity, so we can change the right side from $color{#4257b2}cos 2x$ to $color{#4257b2}sin 2x$ and in this case the equation will be an identity where $color{#4257b2}2sin xcos x=sin 2x$.

$$
text{color{#c34632}The equation is not an identity
\
\
$2sin xcos x=sin 2x$}
$$

(a) We would like to determine the values of $color{#4257b2}a, b$ and $color{#4257b2}c$ if we know that the expression $color{#4257b2}2cos^{2}x+4sin xcos x$ can be written in the form
$color{#4257b2}a sin 2x+b cos 2x +c$. First, we need to simplify our expression to be on the same form $color{#4257b2}a sin 2x+b cos 2x+c$ and then compare the expression with the form to determine the values of $color{#4257b2}a, b$ and $color{#4257b2}c$.

$$
begin{align*}
2cos^{2}x+4sin xcos x&=2cos^{2}x+2left(2sin xcos xright)
end{align*}
$$

Now we note that our expression contains the term $color{#4257b2}2sin xcos x$ which is on the same form of the double angle formula for the sine function where $color{#4257b2}sin 2x=2sin xcos x$, so we can replace $color{#4257b2}2sin xcos x$ from our expression by $color{#4257b2}sin 2x$.

$$
begin{align*}
2cos^{2}x+4sin xcos x&=2cos^{2}x+2left(2sin xcos xright)
\ \
&=2cos^{2}x+2sin 2x
end{align*}
$$

Now we note that our expression contains the term $color{#4257b2}2cos^{2}x$ but we know that the double angle formula for the cosine function is $color{#4257b2}cos 2x=2cos^{2}x-1$, so we can add and subtract $1$ to our expression to have the term $color{#4257b2}2cos^{2}x-1$ which is equivalent to $color{#4257b2}cos 2x$.

$$
begin{align*}
2cos^{2}x+4sin xcos x&=2cos^{2}x+2left(2sin xcos xright)
\ \
&=2cos^{2}x+2sin 2x
\ \
&=2cos^{2}x+2sin 2x+1-1
\ \
&=left(2cos^{2}x-1right)+2sin 2x+1
\ \
&=cos 2x+2sin 2x+1
\ \
&=2sin 2x+cos 2x+1
end{align*}
$$

Now we note that our expression is equivalent to $color{#4257b2}2sin 2x+cos 2x+1$ which is on the same form of $color{#4257b2}a sin 2x+b cos 2x +c$, so by comparing our expression by this form we find that $boxed{ color{#4257b2}a=2, b=1 }$ and $boxed{ color{#4257b2}c=1 }$.

(b) We would like to determine the values of $color{#4257b2}a, b$ and $color{#4257b2}c$ if we know that the expression $color{#4257b2}-2sin xcos x-4sin^{2}x$ can be written in the form
$color{#4257b2}a sin 2x+b cos 2x +c$. First, we need to simplify our expression to be on the same form $color{#4257b2}a sin 2x+b cos 2x+c$ and then compare the expression with the form to determine the values of $color{#4257b2}a, b$ and $color{#4257b2}c$. We note that our expression contains the term $color{#4257b2}-2sin xcos x$ which is on the same form of the double angle formula for the sine function where $color{#4257b2}sin 2x=2sin xcos x$, so we can replace $color{#4257b2}2sin xcos x$ from our expression by $color{#4257b2}sin 2x$.

$$
begin{align*}
-2sin xcos x-4sin^{2}x&=-sin 2x-4sin^{2}x
\ \
&=-sin 2x+2left(-2sin^{2}xright)
end{align*}
$$

Now we note that our expression contains the term $color{#4257b2}-2sin^{2}x$ but we know that the double angle formula for the cosine function is $color{#4257b2}cos 2x=1-2sin^{2}x$, so we can add and subtract $1$ to this term in our expression to have the term $color{#4257b2}1-2sin^{2}x$ which is equivalent to $color{#4257b2}cos 2x$.

$$
begin{align*}
-2sin xcos x-4sin^{2}x&=-sin 2x-4sin^{2}x
\ \
&=-sin 2x+2left(-2sin^{2}xright)
\ \
&=-sin 2x+2left(-2sin^{2}x+1-1right)
\ \
&=-sin 2x+2left[left(1-2sin^{2}xright)-1right]
\ \
&=-sin 2x+2left(cos 2x-1right)
\ \
&=-sin 2x+2cos 2x-2
end{align*}
$$

Now we note that our expression is equivalent to $color{#4257b2}-sin 2x+2cos 2x-2$ which is on the same form of $color{#4257b2}a sin 2x+b cos 2x +c$, so by comparing our expression by this form we find that $boxed{ color{#4257b2}a=-1, b=2 }$ and $boxed{ color{#4257b2}c=-2 }$.

$color{#c34632}(a) a=2, b=1{color{Black$ text{and}} $c=1$}
\
\
Large$$text{color{#c34632}(b) a=-1, b=2{color{Black$ text{and}} $c=-2$}}$

We would like to express $color{#4257b2}8cos^{4}x$ in the form $color{#4257b2}a cos 4x+b cos 2x +c$ and state the values of $color{#4257b2}a, b$ and $color{#4257b2}c$. First, we know that $color{#4257b2}left(2cos^{2}xright)^{2}=4cos^{4}x$, so we can rewrite our expression as $color{#4257b2}2cdot left(2cos^{2}xright)^{2}$.

$$
begin{align*}
8cos^{4}x&=2cdot left(2cos^{2}xright)^{2}
end{align*}
$$

Now we note that our expression contains the term $color{#4257b2}2cos^{2}x$ but we know that the double angle formula for the cosine function is $color{#4257b2}cos 2x=2cos^{2}x-1$, so we can add and subtract $1$ to our expression to have the term $color{#4257b2}2cos^{2}x-1$ which is equivalent to $color{#4257b2}cos 2x$.

$$
begin{align*}
8cos^{4}x&=2cdot left(2cos^{2}xright)^{2}
\ \
&=2cdot left(2cos^{2}x+1-1right)^{2}
\ \
&=2cdot left[left(2cos^{2}x-1right)+1right]^{2}
\ \
&=2cdot left(cos 2x+1right)^{2}
end{align*}
$$

Now we can distribute the exponent where $color{#4257b2}(a+b)^{2}=a^{2}+2ab+b^{2}$.

$$
begin{align*}
cos^{4}x&=2cdot left(cos 2x+1right)^{2}
\ \
&=2cdot left(cos^{2}2x+2cos 2x+1right)
\ \
&=2cos^{2}2x+4cos 2x+2
end{align*}
$$

Now we note that our expression contains the term $color{#4257b2}2cos^{2}2x$ but we know that the double angle formula for the cosine function is $color{#4257b2}cos 4x=2cos^{2}2x-1$, so we can add and subtract $1$ to our expression to have the term $color{#4257b2}2cos^{2}2x-1$ which is equivalent to $color{#4257b2}cos 4x$.

$$
begin{align*}
8cos^{4}x&=2cos^{2}2x+4cos 2x+2
\ \
&=2cos^{2}2x+4cos 2x+2+1-1
\ \
&=left(2cos^{2}2x-1right)+4cos 2x+3
\ \
&=cos 4x+4cos 2x+3
end{align*}
$$

Now we note that our expression is on the same form of $color{#4257b2}a cos 4x+b cos 2x +c$ and by comparing our expression by this form we find that $boxed{ color{#4257b2}a=1, b=4 }$ and $boxed{ color{#4257b2}c=3 }$.

$$text{color{#c34632}a=1, b=4{color{Black$ text{and}} $c=3$}}$