
All Solutions
Section 6-6: Modelling with Trigonometric Functions
y=3cosleft(dfrac{2}{3}left(x+dfrac{pi}{4} right) right)+2
$$
$y=3cosleft(dfrac{2}{3}left(dfrac{pi}{2}+dfrac{pi}{4} right) right)+2$
$y=3cosleft(dfrac{2}{3}left( dfrac{3pi}{4}right) right)+2$
$y=3 cosleft(dfrac{pi}{2} right)+2$
$y=0+2$
$y=2$
For $x=dfrac{3pi}{4}$
$y=3cosleft(dfrac{2}{3}left(dfrac{3pi}{4}+dfrac{pi}{4} right) right)+2$
$y=3cosleft(dfrac{2}{3}(pi) right)+2$
$y=3(-0.5)+2$
$y=-1.5+2$
$y=0.5$
$y= 3 cosleft( dfrac{2}{3}left(dfrac{11pi}{6}+dfrac{pi}{4} right)right)+2$
$y=3cosleft(dfrac{2}{3}left(dfrac{25pi}{12} right) right)+2$
$y=3cosleft(dfrac{25pi}{18} right)+2$
$y=0.97394$
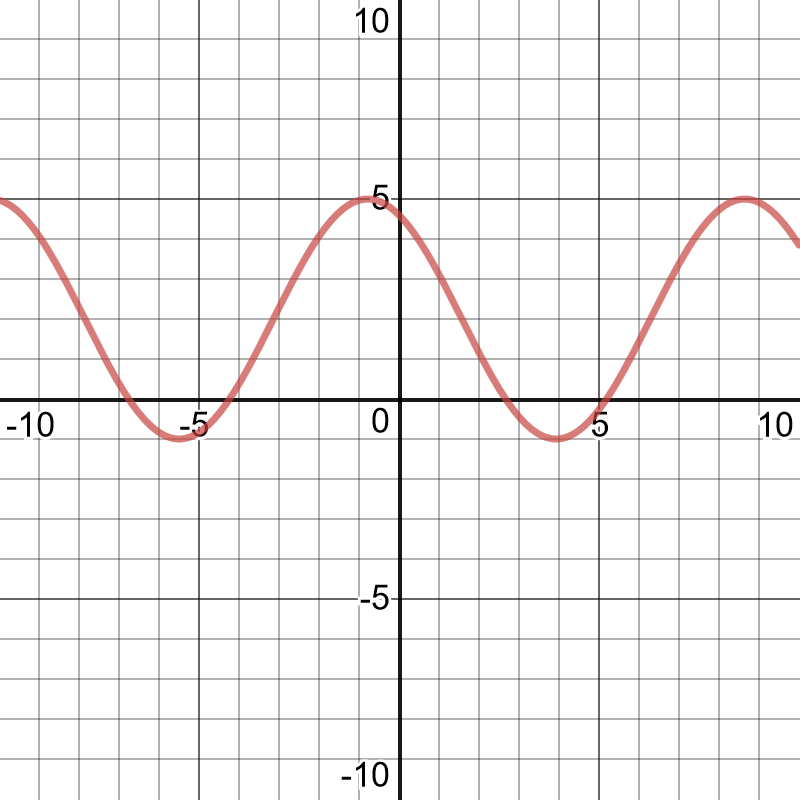
The amplitude represents the radius of the circle in which the tip of the sparkler is moving.
#### (b)
The period represents the time it takes Mike to make one complete circle with the sparkler.
#### (c)
The equation of the axis represents the height above the ground of the centre of the circle in which the tip of the sparkler is moving.
#### (d)
A cosine function should be used because the starting point is at the highest point.
$k=dfrac{2pi}{24}=dfrac{pi}{12}$
$y=90sinleft(dfrac{pi}{12}x right)+30$
period$=3$ seconds
$k=dfrac{2pi}{3}$
$y=250cosleft(dfrac{2pi}{3}x right)+750$.
Circumference$=2pi(1.25)=2.5pi$
$k=dfrac{2pi}{2.5pi}=dfrac{4}{5}$
$y=-1.25sinleft( dfrac{4}{5}xright)+1.5$
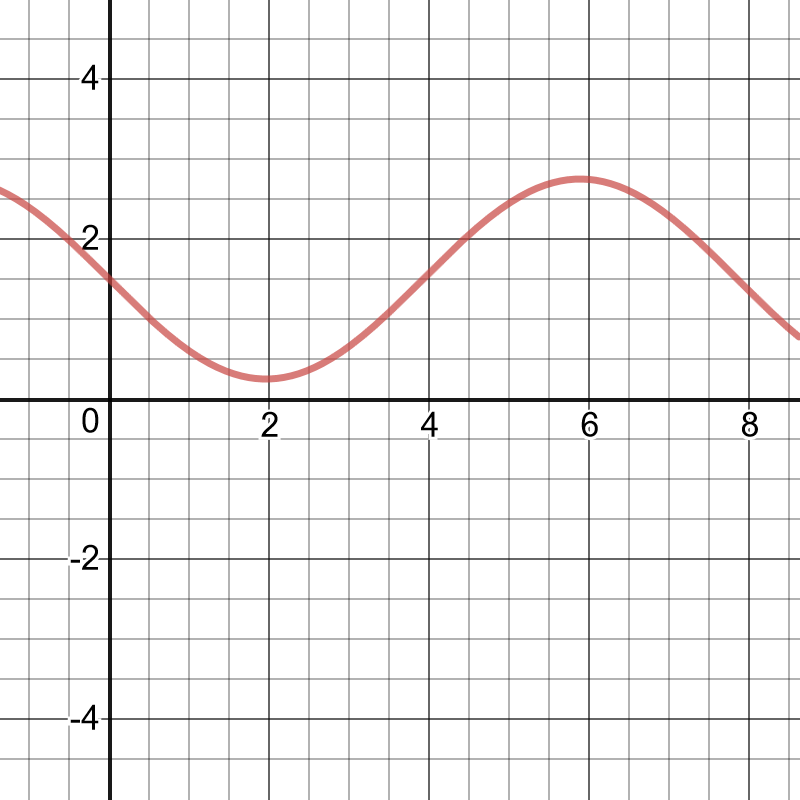
$3.48$ min $< t < 4.02$ min
$5.98$ min $< t < 6.52$ min
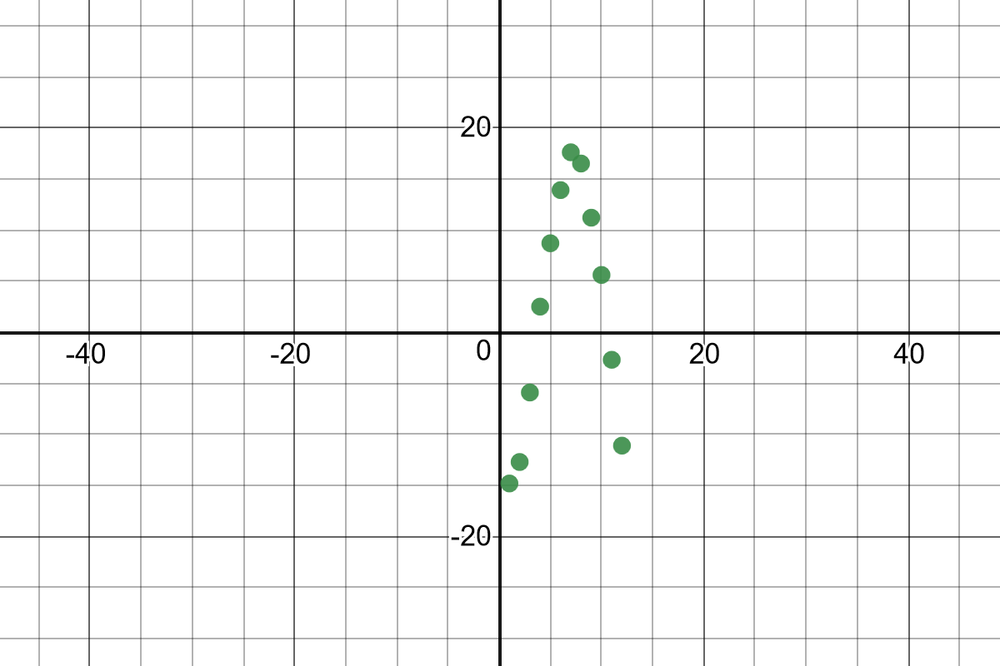
The amplitude of the function is $dfrac{15.7-8.3}{2}=3.7$ with the equation of the axis being $y=dfrac{8.3+15.7}{2}$ or $y=12$.
period$=365$ days
$k=dfrac{2pi}{365}$
$y=3.7sinleft(dfrac{2pi}{365}x right)+12$
#### (b)
For $x=30$
$y=3.7sinleft(dfrac{2pi}{365}(30) right)+12$
$y=13.87$ hours
$k=dfrac{2pi}{365}$
$T(t)=16.2sinleft(dfrac{2pi}{365}(t-116) right)+1.4$
Graph the equation on a graphing calculator to determine when the temperature is below $0 ^{circ}C$.
$0<t<111$ and $304<t<365$
The period of the minute hand is 60.
$k=dfrac{2pi}{60}=dfrac{pi}{30}$
minute hand: $D(t)=15cosleft(dfrac{pi}{30}t right)+300$;
The period of the second hand is $1$.
$k=dfrac{2pi}{1}=2pi$
second hand: $D(t)=15cos(2pi t)+300$;
The period of the hour hand is $720$.
$k=dfrac{2pi}{720}=dfrac{pi}{360}$
hour hand: $D(t)=8cosleft(dfrac{pi}{360}t right)+300$

