We $textbf{will substitute}$ both values of $x$ in equation and if both sides are equal, that means that $-2$ and $3$ are solutions.So, we have next:

First, we will substitute $x=-2$:

$dfrac{2}{x}=dfrac{x-1}{3}$

$dfrac{2}{-2}=dfrac{-2-1}{3}$

$-1=-1$

So, we can conclude that $x=-2$ $textbf{is solution of this equation}$.

Now, we will substitute $x=3$:

$dfrac{2}{x}=dfrac{x-1}{3}$

$dfrac{2}{3}=dfrac{3-1}{3}$

$dfrac{2}{3}=dfrac{2}{3}$

So, we can conclude that $x=dfrac{2}{3}$ $textbf{is solution of this equation}$.

Yes, $x=-2$ and $x=3$ are solutions

In solving this task we will use that the zeros of a rational function are the zeros of the function in the numerator.

#### (a)

$dfrac{x+3}{x-1}=0 Leftrightarrow x+3=0 Leftrightarrow x=-3$

#### (b)

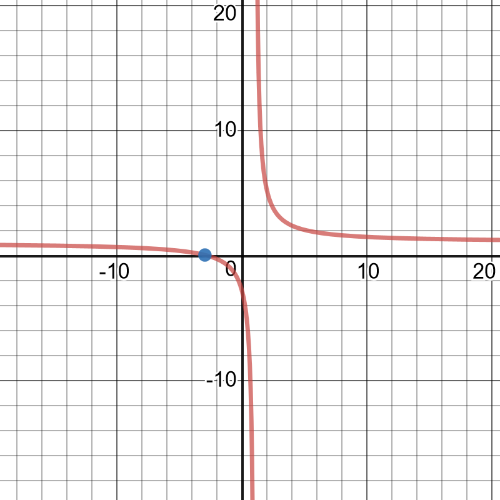
$dfrac{x+3}{x-1}=2 Leftrightarrow dfrac{x+3}{x-1}-2=0 Leftrightarrow dfrac{x+3-2(x-1)}{x-1}=0 Leftrightarrow x+3-2(x-1)=0 Leftrightarrow$

$$
Leftrightarrow x+3-2x+2=0 Leftrightarrow -x+5=0 Leftrightarrow x=5
$$

#### (c)

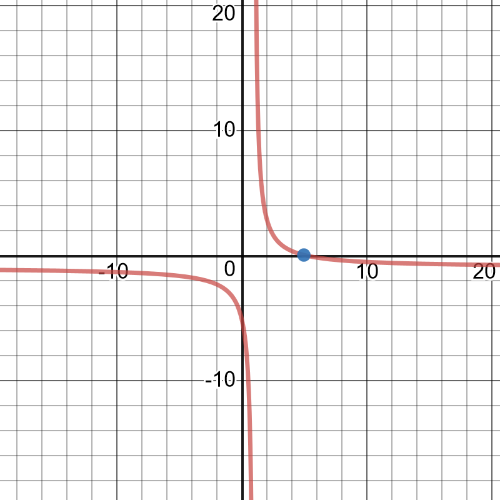
$dfrac{x+3}{x-1}=2x+1 Leftrightarrow dfrac{x+3}{x-1}-(2x+1)=0 Leftrightarrow dfrac{x+3-(2x+1)(x-1)}{x-1}=0 Leftrightarrow$

$Leftrightarrow x+3-(2x+1)(x-1)=0 Leftrightarrow x+3-(2x^2-2x+x-1)=0 Leftrightarrow$

$$
Leftrightarrow -2x^2+2x-4=0 Leftrightarrow x=2, x=-1
$$

#### (d)

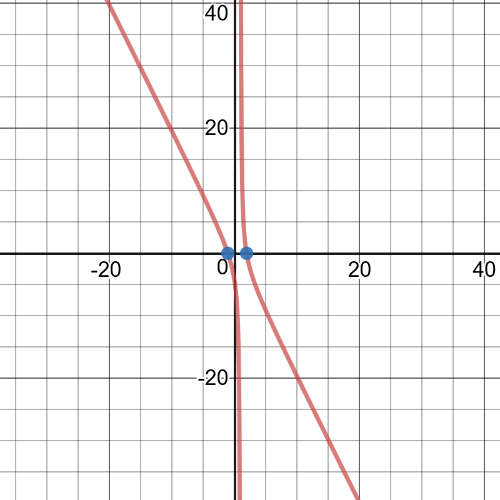
$dfrac{3}{3x+2}=dfrac{6}{5x} Leftrightarrow dfrac{3}{3x+2}-dfrac{6}{5x}=0 Leftrightarrow dfrac{3cdot5x-6(3x+2)}{5x(3x+2)}=0 Leftrightarrow$

$$
Leftrightarrow 15x-6(3x+2)=0 Leftrightarrow 15x-18x-12=0 Leftrightarrow -3x=12 Leftrightarrow x=-4
$$

(a) $x=-3$; (b) $x=5$; (c) $x=-1$, $x=2$; (d) $x=-4$

We will move all equations on one side, on that way on the other side will left only $0$.

#### (a)

$$
dfrac{x-3}{x+3}-2=0
$$

#### (b)

$$
dfrac{3x-1}{x}-dfrac{5}{2}=0
$$

#### (c)

$$
dfrac{x-1}{x}-dfrac{x+1}{x+3}=0
$$

#### (d)

$$
dfrac{x-2}{x+3}-dfrac{x-4}{x+5}=0
$$

(a)$dfrac{x-3}{x+3}-2=0$; (b) $dfrac{3x-1}{x}-dfrac{5}{2}=0$; (c) $dfrac{x-1}{x}-dfrac{x+1}{x+3}=0$;
(d) $dfrac{x-2}{x+3}-dfrac{x-4}{x+5}=0$

#### (a)

$dfrac{x-3}{x+3}=2$

$(x+3)cdotdfrac{x-3}{x+3}=2(x+3)$

$x-3=2x+6$

$x=-9$

So, $textbf{the solution}$ of this equation is $x=-9$.

#### (b)

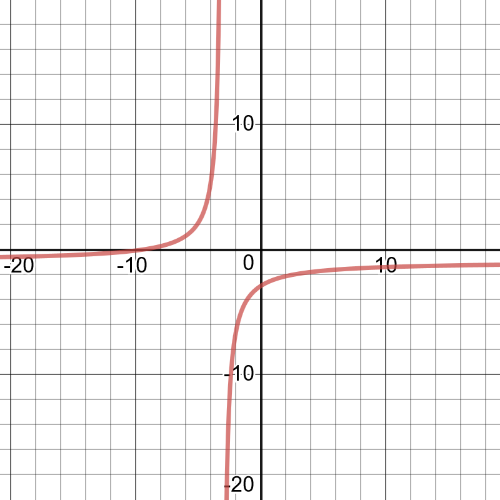
$dfrac{3x-1}{x}=dfrac{5}{2}$

$(3x-1)2=5x$

$6x-2=5x$

$x=2$

So, $textbf{the solution}$ of this equation is $x=2$.

#### (c)

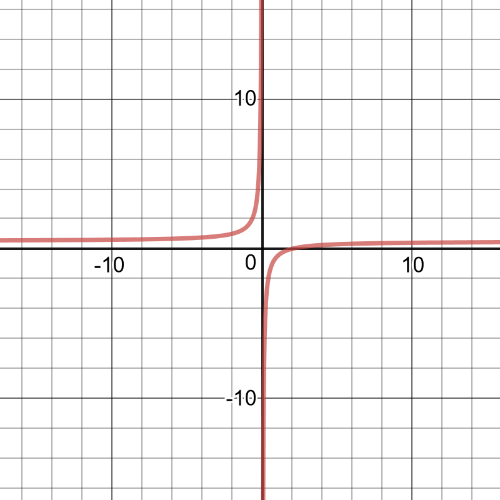
$dfrac{x-1}{x}=dfrac{x+1}{x+3}$

$(x-1)(x+3)=x(x+1)$

$x^2+3x-x-3=x^2+x$

$x=3$

So, $textbf{the solution}$ of this equation is $x=3$.

#### (d)

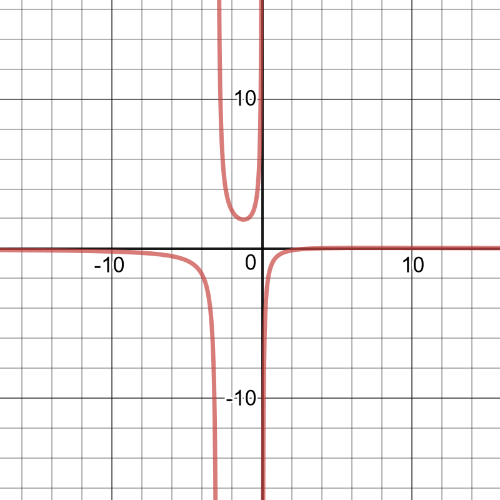
$dfrac{x-2}{x+3}=dfrac{x-4}{x+5}$

$(x-2)(x+5)=(x-4)(x+3)$

$x^2+5x-2x-10=x^2+3x-4x-12$

$4x=-2$

$x=-dfrac{2}{4}=-dfrac{1}{2}$

So, $textbf{the solution}$ of this equation is $x=-dfrac{1}{2}$

(a) $x=-9$; (b) $x=2$; (c) $x=3$; (d) $x=-dfrac{1}{2}$

#### (a)

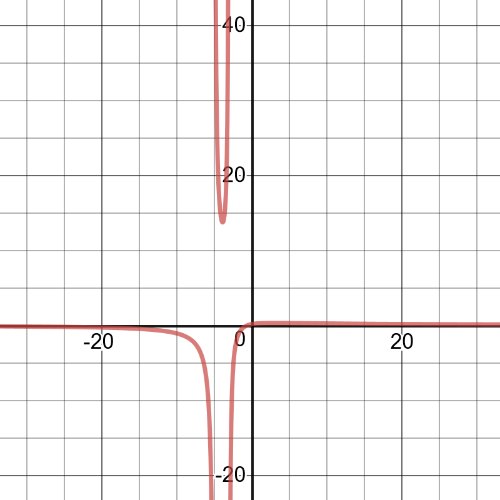
$dfrac{2}{x}+dfrac{5}{3}=dfrac{7}{x}$ /$cdot(3x)$

$3cdot2+5x=7cdot3$

$6+5x=21$

$5x=21-6=15$

$x=dfrac{15}{5}=3$

So, $textbf{the solution}$ of this equation is $x=3$
#### (b)

$dfrac{10}{x+3}+dfrac{10}{3}=6$/$cdot3(x+3)$

$10cdot3+10(x+3)=6cdot3(x+3)$

$30+10x+30=18x+54$

$60+10x=18x+540$

$-8x=-60$

$x=dfrac{6}{8}=dfrac{3}{4}$

So, $textbf{the solution}$ of this equation is $x=dfrac{3}{4}$
#### (c)

$dfrac{2x}{x-3}=1-dfrac{6}{x-3}$/$cdot(x-3)$

$2x=x-3-6$

$x=-9$

So, $textbf{the solution}$ of this equation is $x=-9$

#### (d)

$dfrac{2}{x+1}+dfrac{1}{x+1}=3$/$cdot(x+1)$

$2+1=3(x+1)$

$3=3(x+1)$

$1=x+1$

$x=0$

So, $textbf{the solution}$ of this equation is $x=0$

#### (fe

$dfrac{2}{2x+1}=dfrac{5}{4-x}$ $cdot(2x+1)(4-x)$

$2(4-x)=5(2x+1)$

$8-2x=10x+5$

$-12x=-3$

$x=dfrac{3}{12}=dfrac{1}{4}$

#### (d)

$dfrac{2}{x+1}+dfrac{1}{x+1}=3$/$cdot(x+1)$

$2+1=3(x+1)$

$3=3(x+1)$

$1=x+1$

$x=0$

So, $textbf{the solution}$ of this equation is $x=dfrac{1}{4}$.
#### (f)

$dfrac{5}{x-2}=dfrac{4}{x+3}$ $/cdot(x-2)(x+3)$

$5(x+3)=4(x-2)$

$5x+15=4x-8$

$x=-23$

#### (d)

$dfrac{2}{x+1}+dfrac{1}{x+1}=3$/$cdot(x+1)$

$2+1=3(x+1)$

$3=3(x+1)$

$1=x+1$

$x=0$

So, $textbf{the solution}$ of this equation is $x=-23$.

(a) $x=3$; (b) $x=dfrac{3}{4}$; (c) $x=-9$; (d) $x=0$; (e) $x=dfrac{1}{4}$; (f) $x=-23$

#### (a)

$dfrac{2x}{x+1}=dfrac{5}{4-x}$ $/cdot(x+1)(4-x)$

$2x(4-x)=5(x+1)$

$8x-2x^2=5x+5$

$2x^2-3x+5=0$

We can cocnclude that this equation $textbf{has no real zeros}$.
#### (b)

$dfrac{3}{x}+dfrac{4}{x+1}=2$ $/cdot{x(x+1)}$

$3(x+1)-4x=2x(x+1)$

$3x+3-4x=2x^2+2x$

$2x^2+3x-3=0$

Solving this quadriatic equation, we get that$textbf{ solutions are }x=-0.5$ and $x=3$.
#### (c)

$dfrac{2x}{5}=dfrac{x^2-5x}{5x}$ $/cdot5x$

$2x^2=x^2-5x$

$x^2+5x=0$

$x(x+5)=0$

Solving this equation we can see that $textbf{solutions are}$ $x=0$ or $x=-5$.

#### (d)

$x+dfrac{x}{x-2}=0$ $/cdot(x-2)$

$x(x-2)+x=0$

$x^2-2x+x=0$

$x^2-x=0$

$x(x-1)=0$

Solving this equation, we can see that $textbf{solutions are}$ $x=0$ or $x=1$.
#### (e)

$dfrac{1}{x+2}+dfrac{24}{x+3}=13$ $/cdot(x+2)(x+3)$

$x+3+24(x+2)=13(x+2)(x+3)$

$x+3+24x+48=13(x^2+3x+2x+6)$

$25x+51=13x^2+65x+78$

$13x^3+40x+27=0$

Solving this equation, we can see that $textbf{solutions are}$ $x=-dfrac{27}{13}$ and $x=-1$.
#### (f)

$-dfrac{2}{x-1}=dfrac{x-8}{x+1}$ $/cdot(x-1)(x+1)$

$-2(x+1)=(x-8)(x-1)$

$-2x-2=x^2-x-8x+8$

$x^2-7x+10=0$

Solving this equation, we can see that $textbf{solutions}$ are $x=5$ and $x=2$.

(a) no real zeros; (b) $x=-0.5$, $x=3$; (c) $x=0$ or $x=-5$; (d) $x=0$ or $x=1$; (e) $x=-dfrac{27}{13}$, $x=-1$; (f) $x=5$, $x=2$

#### (a)

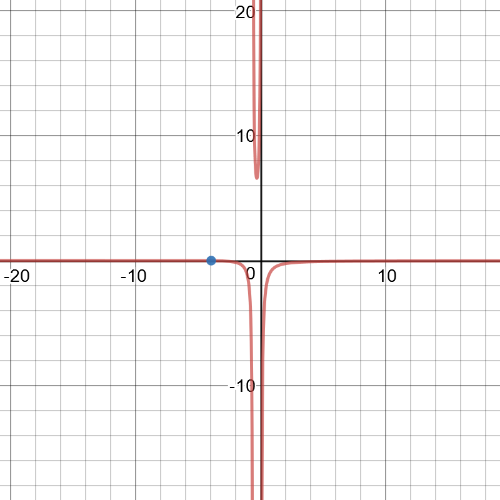
From the graph we can see that $textbf{solution}$ of this equation is $x=6$

#### (b)

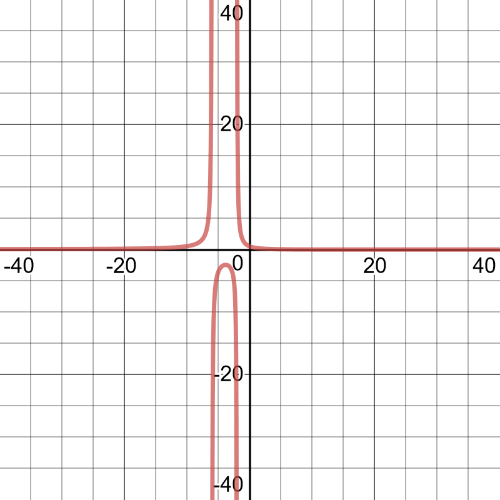
From the graph we can see that $textbf{solutions}$ of this equation are $x= 1.30, 7.70$

#### (c)

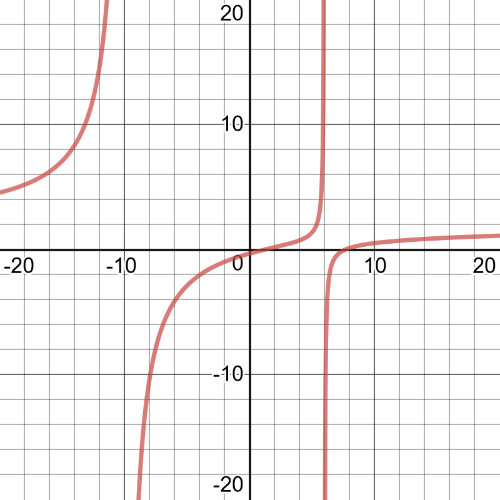
From the graph we can see that $textbf{solution}$ of this equation is $x=10$

#### (d)

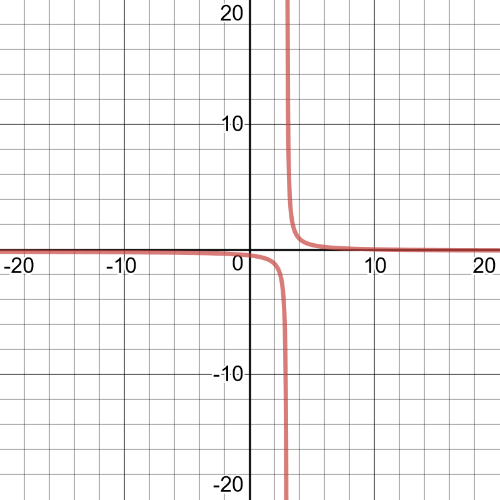
From the graph we can see that $textbf{solutions}$ of this equation are $x= 3.25,20.75$

#### (e)

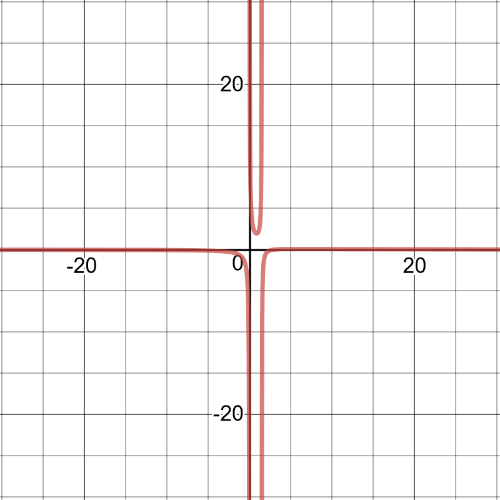
From the graph we can see that $textbf{solutions}$ of this equation are $x=-1.71, 2.71$

#### (f)

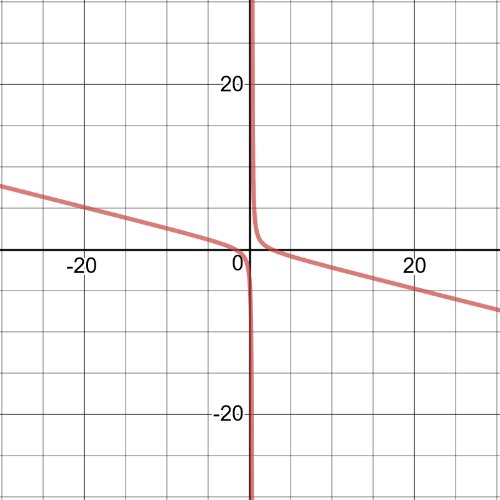
From the graph we can see that $textbf{solutions}$ of this equation are $x= -0.62, 1.62$

#### (a)

$dfrac{x+1}{x-2}=dfrac{x+3}{x-4}$

Multiply both sides of the equation by the $(x-2)(x-4)$.

$(x-2)(x-4)(dfrac{x+1}{x-2})=(x-2)(x-4)(dfrac{x+3}{x-4})$

$(x-4)(x+1)=(x-2)(x+3)$

Simplify.

$x^2-3x-4=x^2+x=6$

Simplify the equation so that $0$ is on one side of the equation.

$x^2-x^2-3x-x-4+6=x^2-x^2+x-x-6+6$

$-4x+2=0$

$-2(2x-1)=0$

Since the product is equal to $0$ one of the factors must be equal to 0.$textbf{ It must be $2x-1$}$ because $2$ is a constant.

$2x-1=0$

$2x-1+1=0+1$

$2x=1$

$dfrac{2x}{2}=dfrac{1}{2}$

$x=dfrac{1}{2}$

#### (b)

Substitute $x=dfrac{1}{2}$ to verify the solution.

$dfrac{dfrac{1}{2}+1}{dfrac{1}{2}-2}=-1$ and $dfrac{dfrac{1}{2}+3}{dfrac{1}{2}-4}= -1$

#### (c)

Graph the equation $dfrac{(x+1)}{(x-2)}-dfrac{(x+3)}{(x-4)}$ and determine the to verify the solution.

$x=dfrac{1}{2}$

We will multiply both sides by a factor $w(15-w)$:

$dfrac{15}{w}=dfrac{w}{15-w}$ $/cdot{w(15-w)}$

$15(15-w)=w^2$

$225-15w=w^2$

$w^2+15w-225=0$

$textbf{Solutions of this quadriatic equation are}$ $w=-15.91$ and $w=0.94$.

Since a width must be positive, we can conclude that $w=0.94$.

Machine A has $dfrac{1}{s}$ boxes per minute and machine B has $dfrac{1}{s+10}$ boxes per minute.

Their combine rate is $dfrac{1}{s}+dfrac{1}{s+10}=15$, we will now solve this equation for $s$:

$dfrac{1}{s}+dfrac{1}{s+10}=15$ $/15s(s+10)$

$15(s+10) 15s=s(s+10)$

$15s+150+15s=s^2+10s$

$s^2-20s-150=0$

From this equation we can conclude that $textbf{machine A takes $s=25.8$ and machine B takes $s=35.8$ minutes}$.

A-$25.8$ minutes and B-$35.8$ minutes

The price per comic in the box that Tayla purchase is $dfrac{300}{s}$, where $s$ is the number of comics in the box. She gave 15 away, and so the number of comics in the box becomes $s-15$. The price per comics in the box when she

resold the box on the Internet then is $dfrac{330}{s-15}$. Tayla made a profit of $1.5 on each comic, which is the sale price per comic minus the original purchase\

price per comic. Solve the equation$$dfrac{330}{s-15}$-$dfrac{300}{s}$=1.50$to find the original number of comics.\$$dfrac{330}{s-15}$-$dfrac{300}{s}$=1.50$\$s(s-15)($dfrac{330}{s-15}$-$dfrac{300}{s}$=1.50)$\$330s-300(s-15)=1.5s(s-15)$\$330s-300s+4500=1.5s^2-22.5s$\$30s+4500=1.5s^2-22.5s$\$30s-30s+4500-4500=1.5s^2-30s-22.5s-4500$\$0=1.5s^2-52.5s-4500$\

The roots are$75.00$and$ -40$. Since you can ‘t have a negative number of comics, the correct answer would be$75$.$textbf{The original price per comic}$

$textbf{would be $dfrac{300}{60}=$ 4 $.}$
{The resale price per comic would be $dfrac{300}{60}=$5.50$.}

$75$ comic books and original price is $4
$$
\
$$

#### (a)

We will substitute $6$ into the formula for $c(t)$ and solve for $t$.

$6=9-90000dfrac{1}{10000+3t}$

$0=3-dfrac{90000}{10000+3t}$ $/(10000+3t)$

$0=3(10000+3t)-90000$

$30000+9t-90000=0$

$9t-60000=0$

$9t=60000$

$t=dfrac{60000}{9}=6666.67$

$$
textbf{After $t=6666.67$ seconds, the concentration will be $6$ $kg/m^3$.}
$$

#### (b)

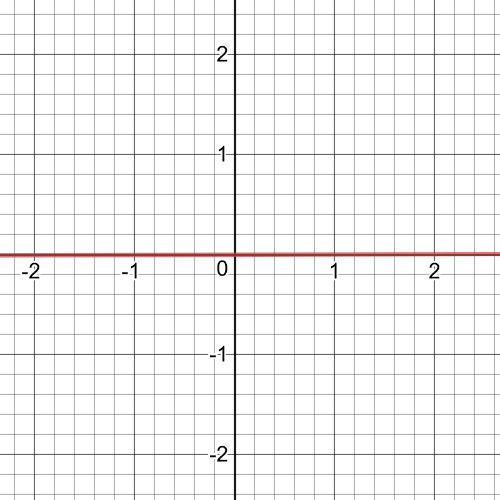
On the following picture there is $textbf{a graph}$ of function $c(t)$.We can see that the function appears to approach $0kg/m^3$ as time increases.

(a) $t=6666.67$ seconds

#### (a)

Tom can fill $dfrac{1}{s}$ of an order in $1$ minute.Paco and Carl’s rates are $dfrac{1}{s-2}$ and $dfrac{1}{s+1}$.Working together Tom and Paco can fill an ordee in about $1$ minute and $20$ seconds, or about $1.33$ minutes.

We will solve $dfrac{1}{s-2}+dfrac{1}{s}=dfrac{1}{1.33}$ to find how long it takes each person to fill an order.

$dfrac{1}{s-2}+dfrac{1}{s}=dfrac{1}{1.33}$ $/s(s-2)$

$1.33s+1.33(s-2)=s(s-2)$

$1.33s+1.33s-2.66=s^2-2s$

$s^2-4.33s+2.66=0$

Solving this quadriatic equation, we can see that $textbf{solutions are}$ $s=3.994$ or $s=0.66$.
Because Paco can fill the order in $2$ minutes less than Tom and because we can not have a negative amount of time, $textbf{Tom’s time}$ must be $3.994$.So, $textbf{Paco can fill the order in about}$ $2$ minutes and $textbf{Carl can fill the order in about}$ $5$.
#### (b)

We will add rates together to find how long it would take to them to fill the order working together.

$dfrac{1}{5}+dfrac{1}{4}+dfrac{1}{2}=0.95$

$dfrac{1}{0.95}=1.05$

$textbf{So, working together they can fill the order in about $1.05$ minute}$.

(a) Tom can fill for about $4$ minutes, Paco can fill in about $2$ minutes and Carl can fill in about $5$ minutes; (b) working together, they will need $1.05$ minute

Answers may vary. For example:$textbf{ You can use either algebra or graphing technology to solve a rational equation}$.With algebra,solving the equation takes more time, but you get an exact answer. With graphing technology, you can solve the equation quickly, but you do not always get an exact answer.

$dfrac{x^2-6x+5}{x^2-2x-3}=dfrac{2-3x}{x^2+3x+3}$

Turn this into an equation that you can graph to find the solutions.

$y=dfrac{x^2-6x+5}{x^2-2x-3}-dfrac{2-3x}{x^2+3x+3}$

Graph the equation.

$$
textbf{The solutions are approximately $x=-3.80, -1.42, 0.90$ and $4.33$.}
$$

$x= -3.80, -1.42, 0.90$ and $4.33$

#### (a)

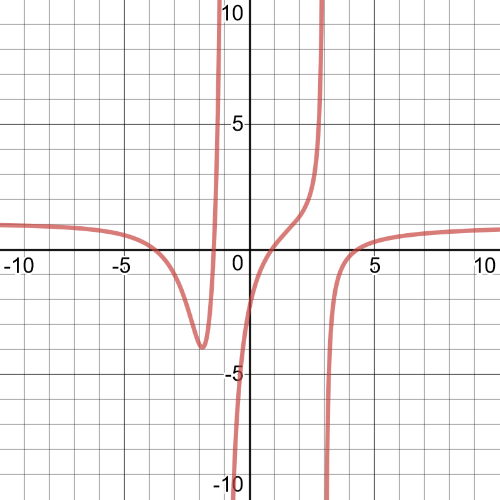
$textbf{The graphs will have the same position when their equation are equal}$. Set the two equations equal to wach other and then solve for $t$. Graph the equation to help you.

$dfrac{7t}{t^2+1}= t+dfrac{5}{t+2}$

$y=t+dfrac{5}{t+2}-dfrac{7t}{t^2+1}$

Graph the equation.

Examine the graph. The zeros are $x=0.438$ and $1.712$

#### (b)

Object A is closer to the origin than object B when

$dfrac{7t}{t^2+1}< t+dfrac{5}{t+2}$ or when

$0< t+dfrac{5}{t+2}-dfrac{7t}{t^2+1}$

Examine the graph and find when the function is positive to solve the inequality. $textbf{The graph shows that the inequality is true on $(0, 0.438)$ and $(1.712, infty)$}$.

a) $x=0.438$ and $1.712$;

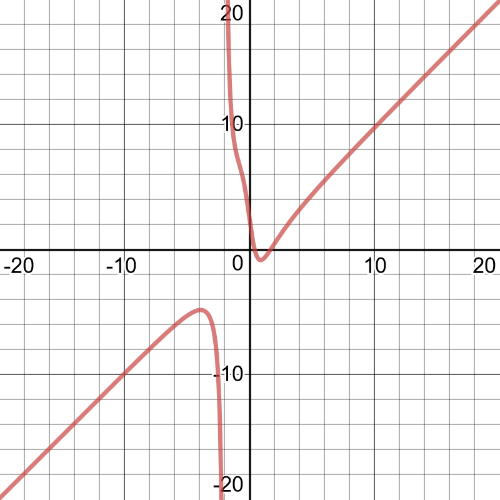
b)$dfrac{7t}{t^2+1}leq t+dfrac{5}{t+2}$ or when

$0leq t+dfrac{5}{t+2}-dfrac{7t}{t^2+1}$