
All Solutions
Section 5-1: Graphs of Reciprocal Functions
$(a) – C$
$(b) – A$
$(c) – D$
$(d) – F$
$(e) – B$
$(f) – E$
Now, we are matching $textbf{reciprocals functon pairs}$:
$(a) – (d)$
$(b) – (f)$
$(c) – (e)$
$(a) – (d)$, $(b) – (f)$, $(c) – (e)$
For the original function $textbf{zero occurs}$ for $x=6$, and $textbf{equation of vertical asymptote}$ for reciprocal function is $x=6$.
#### (b)
For the original function $textbf{zero occurs}$ for $x=-dfrac{4}{3}$, and $textbf{equation of vertical asymptote}$ for reciprocal function is $x=-dfrac{4}{3}$.
#### (c)
For the original function $textbf{zeros occur}$ for $x=5$ and $x=-3$, and $textbf{equations of vertical asymptotes}$ for reciprocal function are $x=5$ and $x=-3$.
#### (d)
For the original function $textbf{zeros occur}$ for $x=pmdfrac{5}{2}$, and $textbf{equations of vertical asymptotes}$ for reciprocal function are $x=pmdfrac{5}{2}$.
#### (e)
Here, original function $textbf{has no zeros}$ and reciprocal function $textbf{has no vertcal asymptotes}$.
#### (f)
For the original function $textbf{zeros occur}$ for $x=-1$ and $x=-dfrac{3}{2}$, and $textbf{equations of vertical asymptotes}$ for reciprocal function are $x=-1$ and $x=-dfrac{3}{2}$.
On the following garph $textbf{red is graph of original function and blue one is graph of reciprocal function}$:
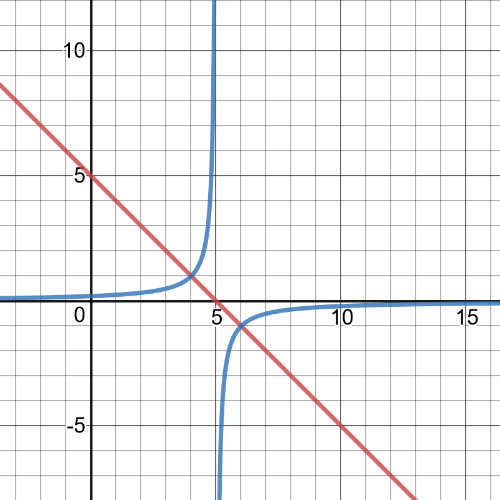
On the following garph $textbf{red is graph of original function and blue one is graph of reciprocal function}$:
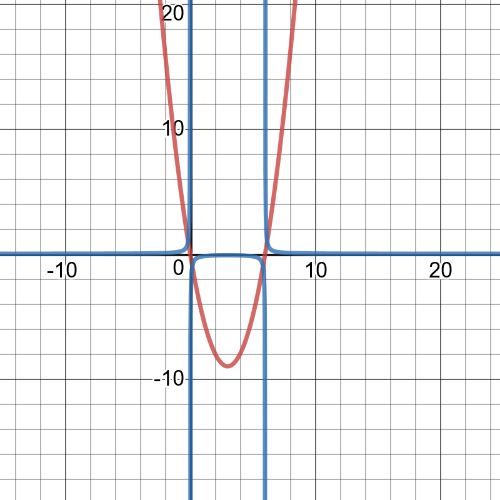

On the following picture red is graph of $f(x)$ and blue one is graph of $dfrac{1}{f(x)}$:
From the graph, we can conclude that $textbf{equation for $y=f(x)$ is\ $y=f(x)=-2x+8$ and reciprocal function is}$ $y=dfrac{1}{f(x)}=dfrac{1}{-2x+8}$.
$textbf{Equation of the reciprocal function is }$:
$y=dfrac{1}{f(x)}=dfrac{1}{2x}$
Equation of $textbf{vertical asimptote}$ of reciprocal function is $x=0$.
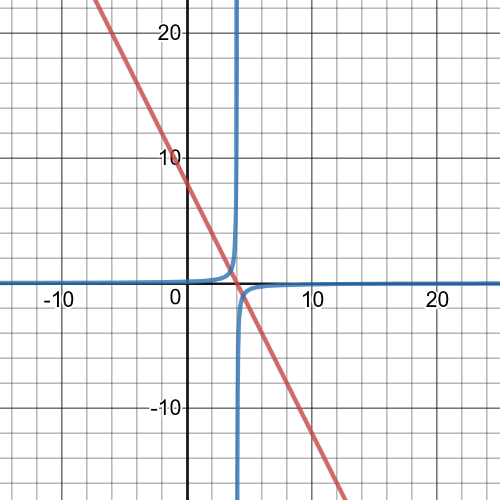
On the following picture red is garph of origin function, blue is of reciprocal function and black is vertical asymptote:
$textbf{Equation of the reciprocal function is }$:
$y=dfrac{1}{f(x)}=dfrac{1}{x+5}$
Equation of $textbf{vertical asimptote}$ of reciprocal function is $x=-5$.
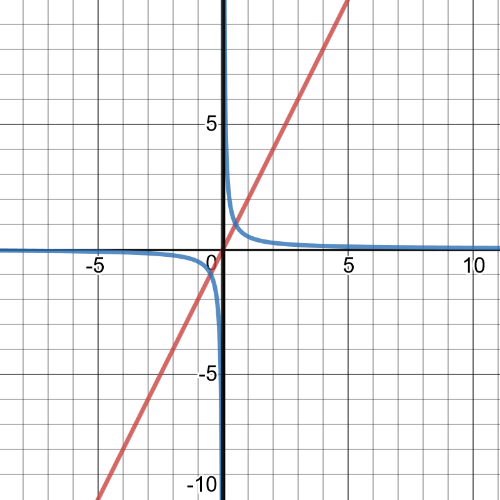
On the following picture red is garph of origin function, blue is of reciprocal function and black is vertical asymptote:
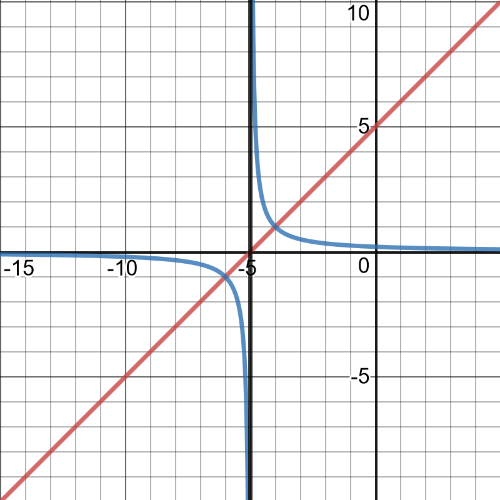
$textbf{Equation of the reciprocal function is }$:
$y=dfrac{1}{f(x)}=dfrac{1}{x-4}$
Equation of $textbf{vertical asimptote}$ of reciprocal function is $x=4$.
On the following picture red is garph of origin function, blue is of reciprocal function and black is vertical asymptote:
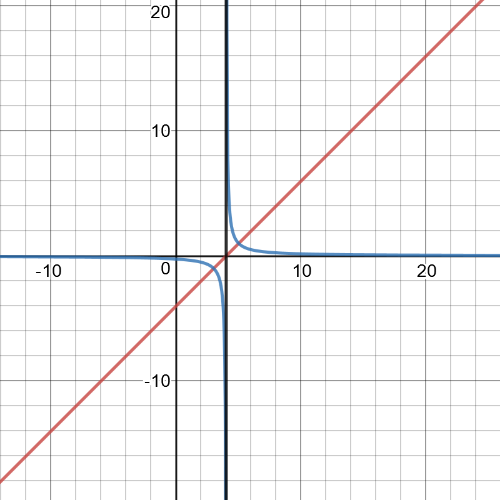
$textbf{Equation of the reciprocal function is }$:
$y=dfrac{1}{f(x)}=dfrac{1}{2x+5}$
Equation of $textbf{vertical asimptote}$ of reciprocal function is $x=-dfrac{5}{2}$.
On the following picture red is garph of origin function, blue is of reciprocal function and black is vertical asymptote:
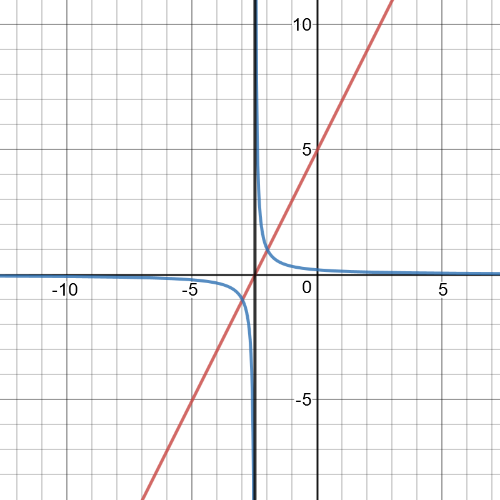
$textbf{Equation of the reciprocal function is }$:
$y=dfrac{1}{f(x)}=dfrac{1}{-3x+6}$
Equation of $textbf{vertical asimptote}$ of reciprocal function is $x=2$.
On the following picture red is garph of origin function, blue is of reciprocal function and black is vertical asymptote:
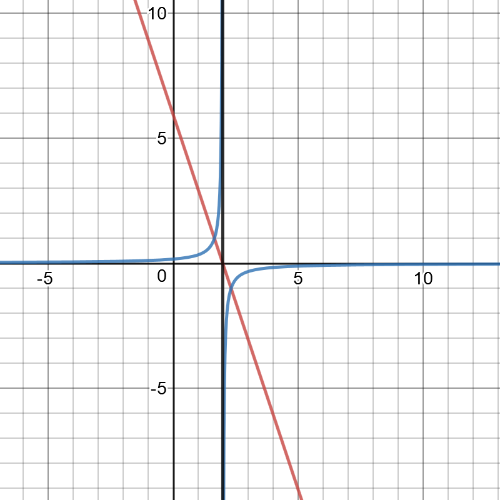
$textbf{Equation of the reciprocal function is }$:
$y=dfrac{1}{f(x)}=dfrac{1}{(x-3)^2}$
Equation of $textbf{vertical asimptote}$ of reciprocal function is $x=3$.
On the following picture red is garph of origin function, blue is of reciprocal function and black is vertical asymptote:
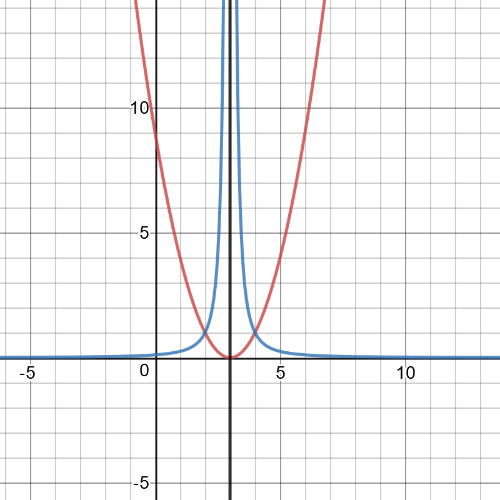
$textbf{Equation of the reciprocal function is }$:
$y=dfrac{1}{f(x)}=dfrac{1}{x^2-3x-10}$
Equations of $textbf{vertical asimptotes}$ of reciprocal function are $x=-2$ and $x=5$.
On the following picture red is garph of origin function, blue is of reciprocal function and black is vertical asymptote:
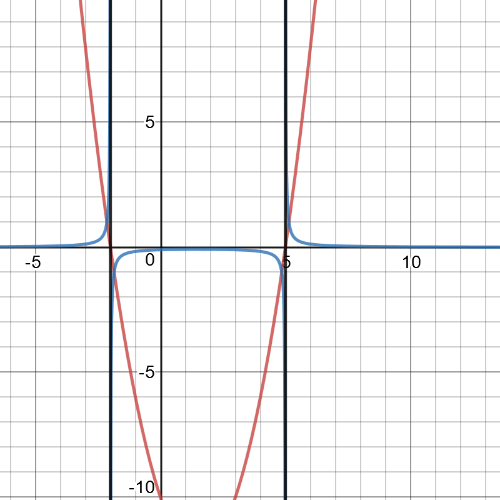
$textbf{Equation of the reciprocal function is }$:
$y=dfrac{1}{f(x)}=dfrac{1}{3x^2-4x-4}$
Equations of $textbf{vertical asimptotes}$ of reciprocal function are $x=-dfrac{2}{3}$ and $x=2$.
On the following picture red is garph of origin function, blue is of reciprocal function and black is vertical asymptote:
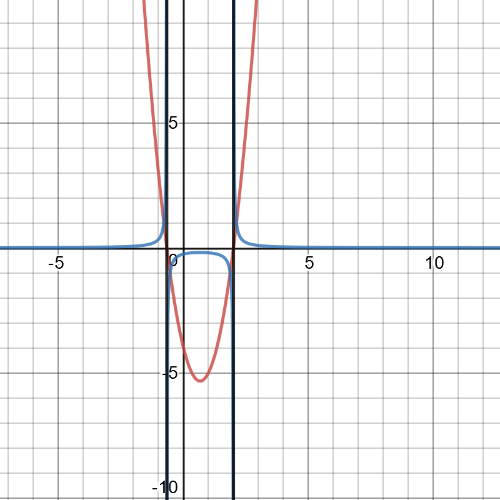
$textbf{Reciprocal function is:}$
$y=dfrac{1}{f(x)}=dfrac{1}{-x-1}$
On the following picture is $textbf{graph of this reciprocal function}$:
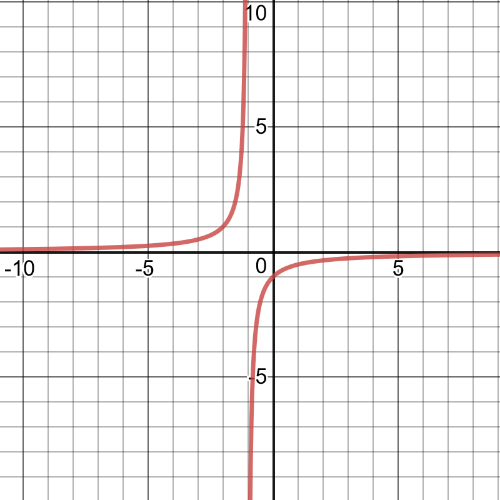
$textbf{Reciprocal function is:}$
$y=dfrac{1}{f(x)}=dfrac{1}{dfrac{2}{3}|x|-2}$
On the following picture is $textbf{graph of this reciprocal function}$:
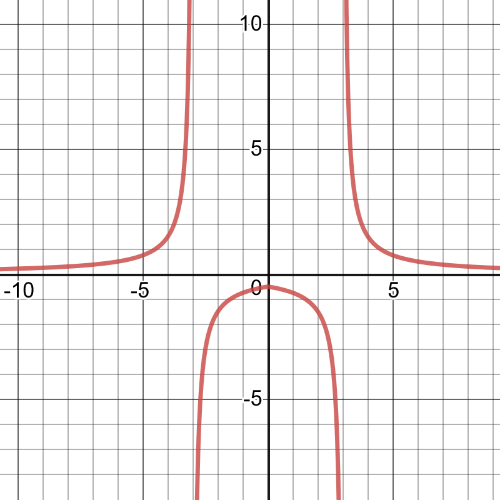
$textbf{Reciprocal function is:}$
$y=dfrac{1}{f(x)}=dfrac{1}{sqrt{36-x^2}}$
On the following picture is $textbf{graph of this reciprocal function}$:
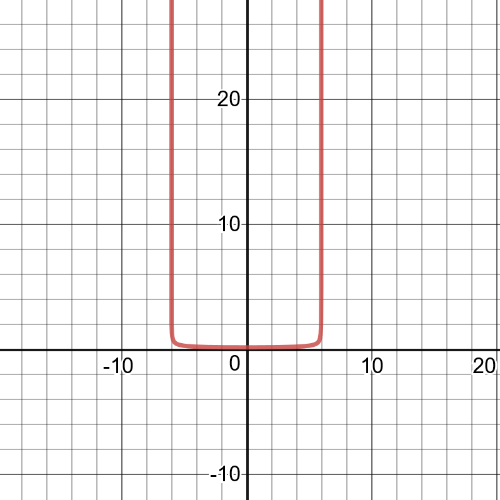
$textbf{Reciprocal function is:}$
$y=dfrac{1}{f(x)}=dfrac{1}{2|x+1|}$
On the following picture is $textbf{graph of this reciprocal function}$:
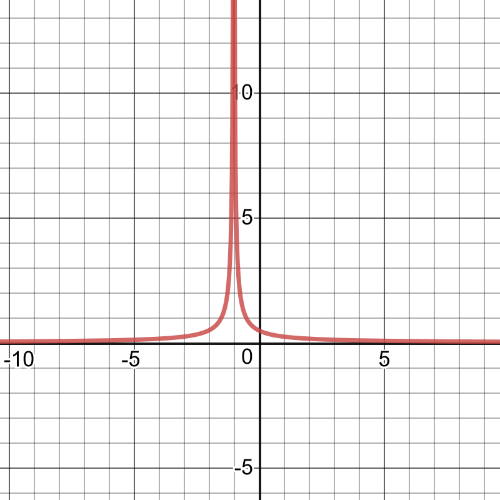
$textbf{Domain}$ of the reciprocal function is set $D=left{xinBbb{R}|xnedfrac{5}{2} right}$ and the $textbf{range}$ is set $R=left{yinBbb{R}|yne0 right}$.On the following picture red is graph of original function and blue one is graph of reciprocal function:
$textbf{Domain}$ of the reciprocal function is set $D=left{xinBbb{R}|xne-dfrac{4}{3} right}$ and the $textbf{range}$ is set $R=left{yinBbb{R}|yne0 right}$.On the following picture red is graph of original function and blue one is graph of reciprocal function:
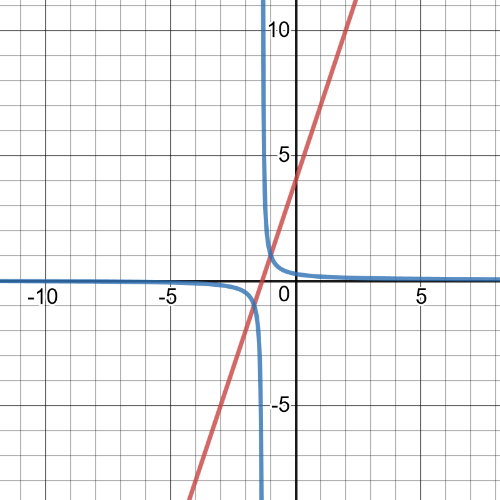
$textbf{Reciprocal function is}$ $y=dfrac{1}{x^2-4}$ and its graph is blue one on following picture while red one is graph of original function:
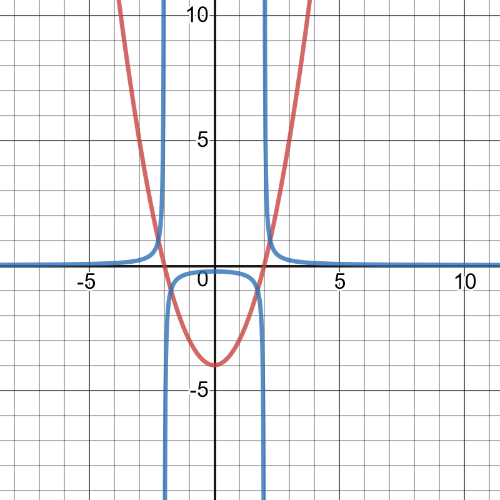
$textbf{Reciprocal function is}$ $y=dfrac{1}{(x-2)^2-3}$ and its graph is blue one on following picture while red one is graph of original function:
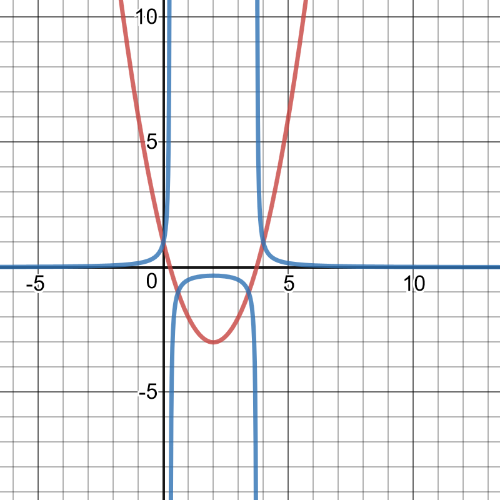
$textbf{Reciprocal function is}$ $y=dfrac{1}{x^2-3x+2}$ and its graph is blue one on following picture while red one is graph of original function:
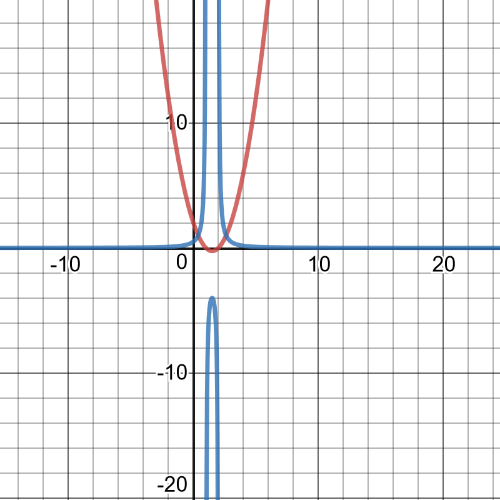
$textbf{Reciprocal function is}$ $y=dfrac{1}{(x+3)^2}$ and its graph is blue one on following picture while red one is graph of original function:
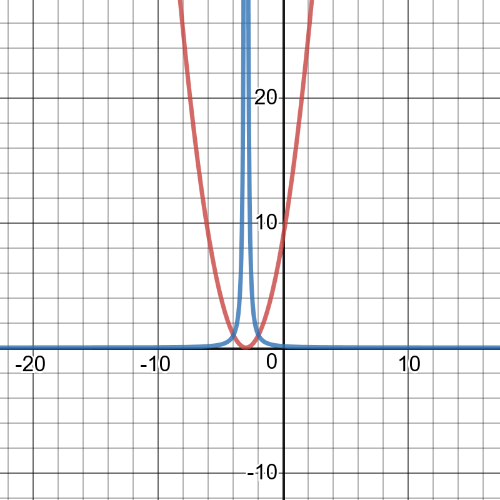
$textbf{Reciprocal function is}$ $y=dfrac{1}{x^2+2}$ and its graph is blue one on following picture while red one is graph of original function:
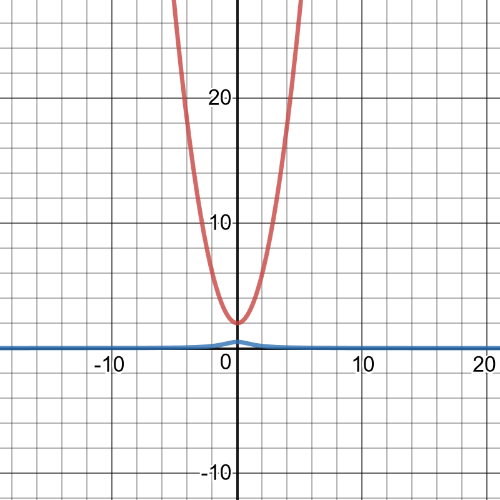
$textbf{Reciprocal function is}$ $y=dfrac{1}{-(x+4)^2+1}$ and its graph is blue one on following picture while red one is graph of original function:
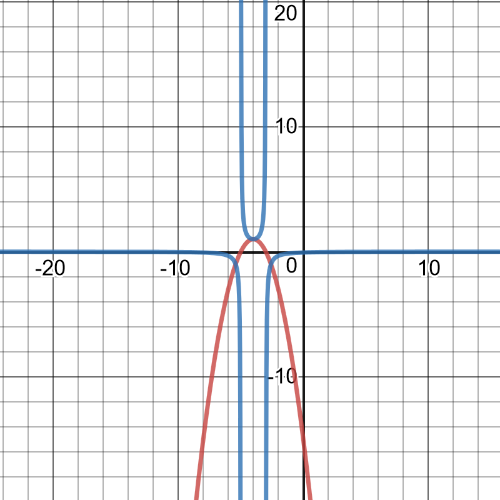
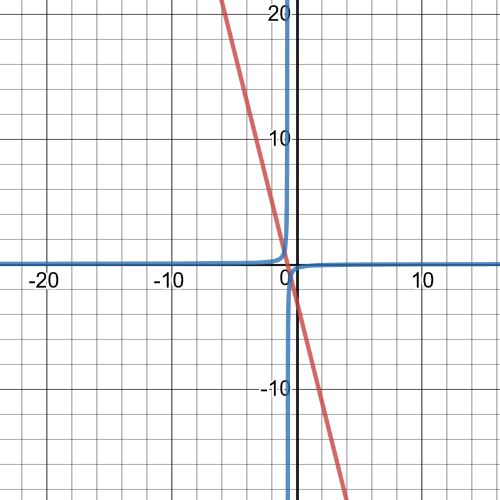
$textbf{The domain and range}$ of this function is set $Bbb{R}$, it is $textbf{increasing}$ on its domain, it is $textbf{positive}$ on interval $(-4,+infty)$ and $textbf{negative}$ on $left(-infty,-4 right]$, points of $textbf{intercepts}$ are: $(-4,0)$ with $x$-axis and $(0,8)$ with $y$-axis.
On following picture red is graph of original function and blue is graph of reciprocal function which is:
$$
y=dfrac{1}{2x+8}
$$
$textbf{The domain and range}$ of this function is set $Bbb{R}$, it is $textbf{decreasing}$ on its domain, it is $textbf{positive}$ on interval $(-infty,-dfrac{3}{4})$ and $textbf{negative}$ on $left[-dfrac{3}{4},+infty right]$, points of $textbf{intercepts}$ are: $(-dfrac{3}{4},0)$ with $x$-axis and $(0,-3)$ with $y$-axis.
On following picture red is graph of original function and blue is graph of reciprocal function which is:
$$
y=dfrac{1}{-4x-3}
$$
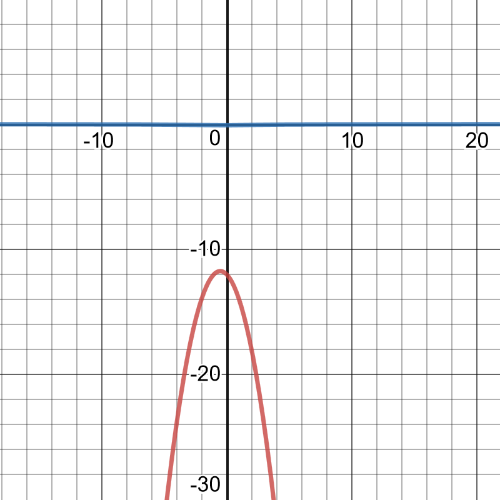
$textbf{The domain}$ of this function is set $Bbb{R}$, and $textbf{range}$ is interval $R=(-infty,-11.75]$, it is $textbf{increasing}$ on interval $(-infty,-0.5)$ and $textbf{decreasing}$ on interval $left[-0.5,+infty right)$, it is $textbf{negative}$ on its domain, point of $textbf{intercept}$ is: $(0,-12)$ with $y$-axis.
On following picture red is graph of original function and blue is graph of reciprocal function which is:
$$
y=dfrac{1}{-x^2-x-12}
$$
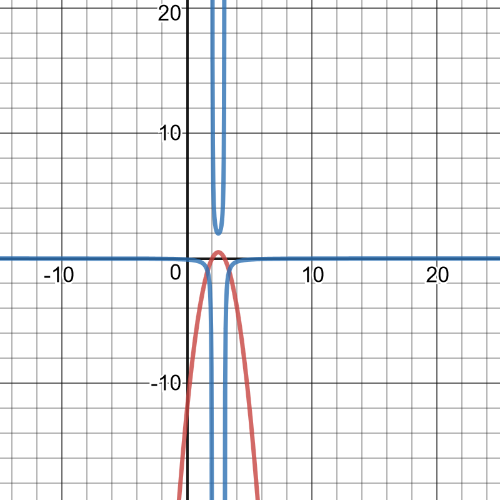
$textbf{The domain}$ of this function is set $Bbb{R}$ and $textbf{range}$ is $R=(-infty,2.5)$, it is $textbf{increasing}$ on interval $(-infty,2.5)$ and $textbf{decreasing}$ on $left[2.5,+infty right]$, it is $textbf{positive}$ on interval $(2,3)$ and $textbf{negative}$ on $left(-infty,2 right]$ $cup$ $left[3,+infty right)$, points of $textbf{intercepts}$ are: $(2,0)$ and $(3,0)$ with $x$-axis.
On following picture red is graph of original function and blue is graph of reciprocal function which is:
$$
y=dfrac{1}{-2x^2+10x-12}
$$
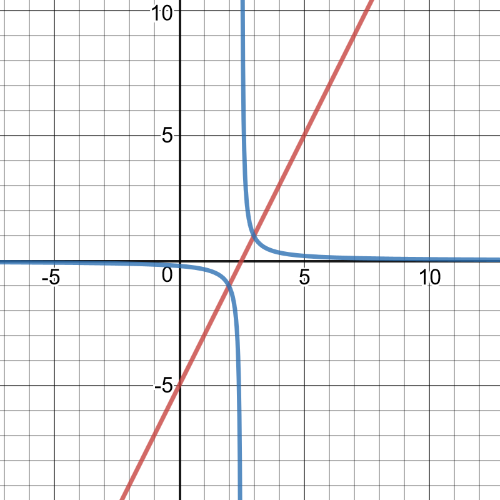
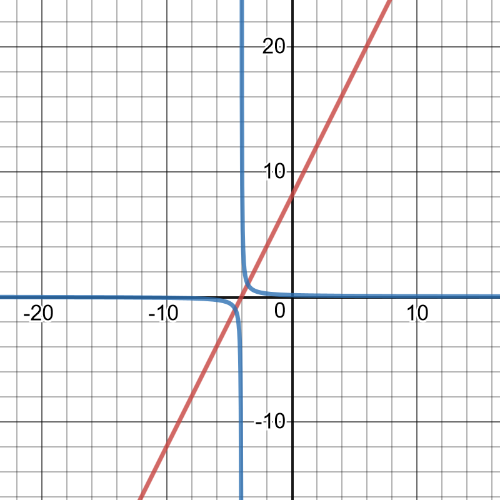
On the following picture is linear function and its reciprocial function, and it has vertical asymptote: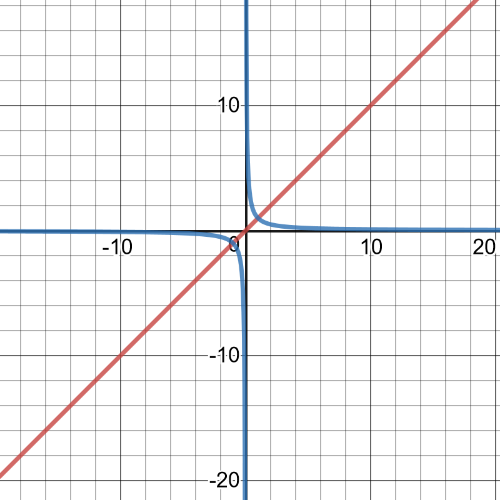
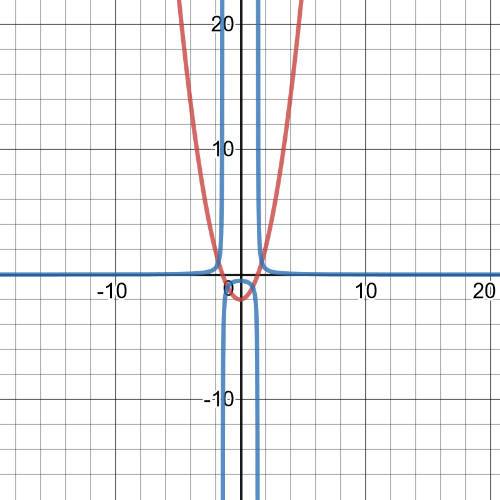
$f(x)=(x+1)(x-1)=x^2-x+x-1=x^2-1$
$textbf{So, the reciprocial function is}$:
$y=dfrac{1}{f(x)}=dfrac{1}{x^2-1}$
On the following picture is $textbf{graph of function $y$}$, and we can see that it matches with given graph.
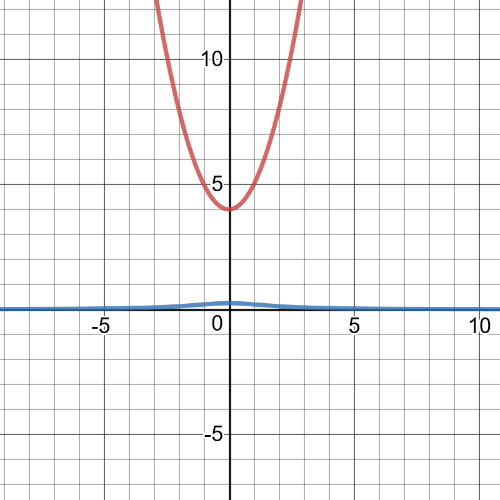
After $20$ s will be left
$b(20)=dfrac{10000}{20}=500$ bacteria.
#### (b)
$5000=dfrac{10000}{t}$ $Rightarrow$ $t=dfrac{10000}{5000}=2$ s
$textbf{So, after $2$ s will be $5000$ bacteria left}$.
#### (c)
$1=dfrac{10000}{t}$ $Rightarrow$ $t=dfrac{10000}{1}=10000$ s
$textbf{So, after $10000$ s will be $1$ bacterium left}$.
#### (d)
$textbf{The disadvantage}$ is that in the initial moment, $t = 0$, we can not calculate the number of bacteria.
#### (e)
$textbf{The domain}$ of this function sholud be $D=left{xinBbb{R}|xne0 right}$, and $textbf{range}$ is $R=left{yinBbb{R}|yne0 right}$.
, $R=left{yinBbb{R}|yne0 right}$
$(1)$ It is $textbf{positive}$ on interval $left[0,+infty right)$ and $textbf{negative}$ on interval $(-infty,0)$;
$(2)$ It is $textbf{decreasing}$ on interval $left[-n,+infty right)$ and $textbf{increasing}$ on inetrval $(-infty,-n)$;
$(3)$ $textbf{Its point of intersect is}$ $(0,dfrac{1}{n})$ with $y$-axis;
$(4)$ It has $textbf{vertical asymptote}$ in $x=-n$.
#### (a)
$textbf{The domain and range}$ of function $g(x)$ are sets:
$D=left{xinBbb{R}|xne-n right}$
$R=left{yinBbb{R}|yne0 right}$
#### (b)
For the family of functions $f(x)=x+n$, $textbf{intercept point}$ with $y$-axis is $(0,n)$, but $textbf{intercept point}$ of family of functions $g(x)$ with $y$-axis is $(0,dfrac{1}{n})$.
#### (c)
These two functions $f(x)$ and $g(x)$ $textbf{will intersect}$ in points $(1-n,1)$ and $(-1-n,-1)$.
$(1)$ All the $y$-coordinates of a reciprocal function are the reciprocals of the $y$-coordinates of the original function.
$(2)$ The graph of a reciprocal function has a vertical asymptote at each zero of the original function.
$(3)$ A reciprocal function will always have $y=0$ as a horizontal asymptote if the original function is linear or quadratic.
$(4)$ A reciprocal function has the same positive/negative intervals as the original function.
$(5)$ Intervals of increase on the original function are intervals of decrease on the reciprocal function. Intervals of decrease on the original function are intervals of increase on the reciprocal function.
$(6)$ If the range of the original function includes $2$ and/or $-2$ the reciprocal function will intersect the original function at a point (or points) where the $y$-coordinate is $2$ or $-2$ .
$(7)$ If the original function has a local minimum point, the reciprocal function will have a local maximum point at the same $x$-value.
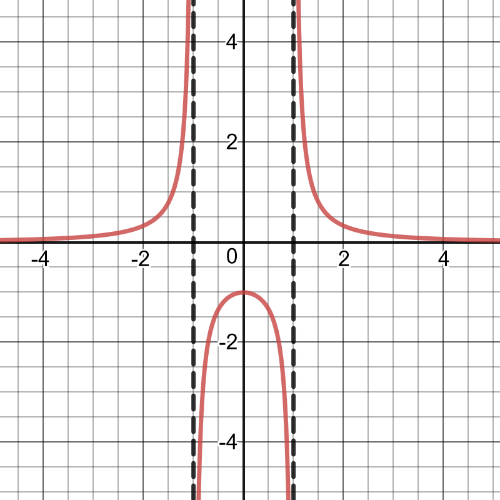
We can see that both functions are negative for $xin(-infty,-2)$ and positive for $xin(-2,+infty)$.The original function is increasing for $xin(-infty,+infty)$.The reciprocal function is decreasing for $xin(-infty,-2)$ or $xin(-2,+infty)$.
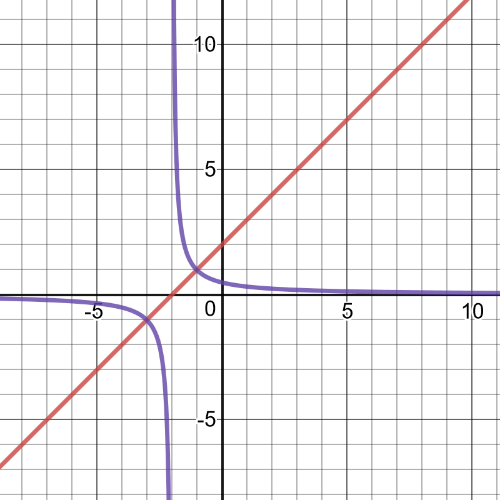
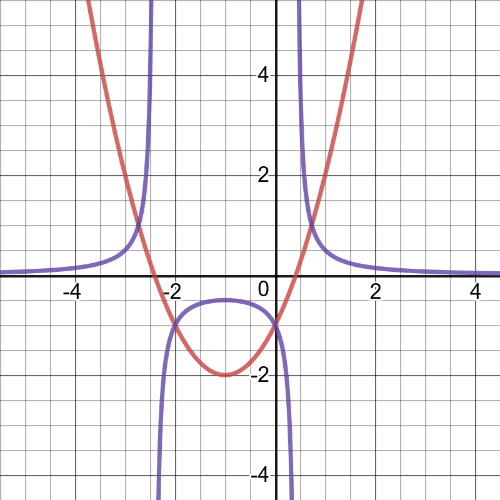
$f(x)=(x+1)^2-2$ and its reciprocal function $y=dfrac{1}{(x+1)^2-2}$.
Both functions are negative for $xin(-2.414,0.414)$ and positive for $xin(-infty,-2.414)$ or $xin(0.414,+infty)$.The original function is decreasing for $xin(-infty,-1)$ and increasing for $xin(-1,+infty)$.The reciprocal function is increasing $xin(-infty,-2.414)$ or $xin(-2.414,-1)$ and decreasing for $xin(-1,1)$ or $xin(1,+infty)$.
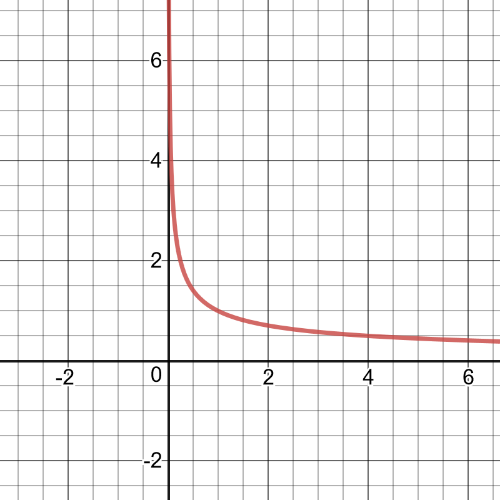
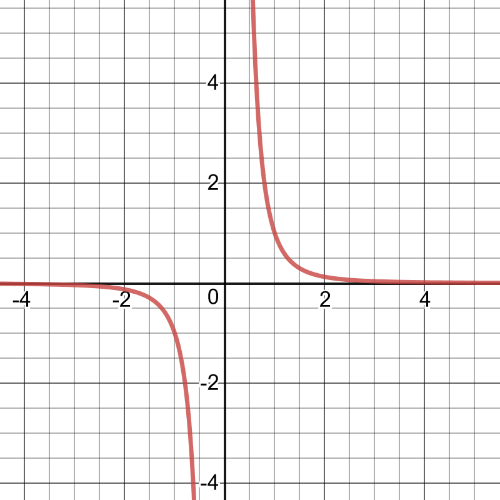
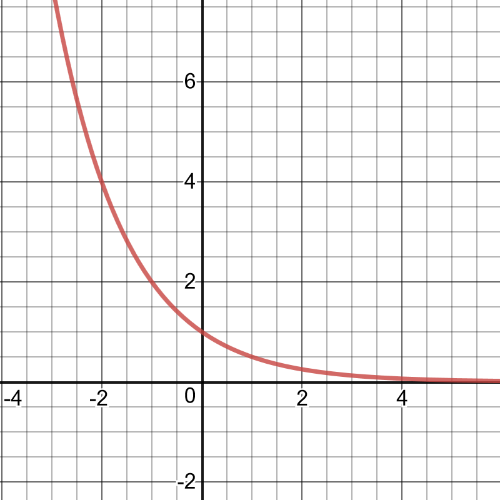
$$
y=dfrac{1}{x+4}
$$

