(a) We would like to solve the inequality $color{#4257b2}(x+2)(x-3)(x+1)geq 0$ using the number line strategy. First, we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
(x+2)(x-3)(x+1)geq 0
$$

$$
(x+2)(x-3)(x+1)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x+2=0, x-3=0 text{or} x+1=0
$$

$$
x=-2, x=3 text{or} x=-1
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

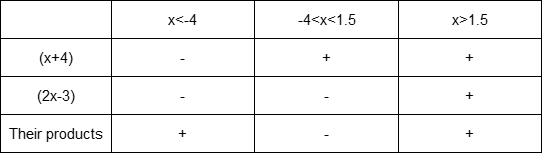
Now we find that the roots are $color{#4257b2}-2, -1$ and $color{#4257b2}3$, so these numbers will divide the domain to four intervals $color{#4257b2}x<-2, -2<x<-1, -1<x3$ and the following number line shows these intervals

Now we have four intervals and we know that our inequality is
$color{#4257b2}(x+2)(x-3)(x+1) geq 0$, so we can let $color{#4257b2}f(x)=(x+2)(x-3)(x+1)$ and then create a table to consider the sign of the function $color{#4257b2}f(x)$ at each interval to know the intervals where this function will be positive or equals zero to verify our inequality $color{#4257b2}(x+2)(x-3)(x+1) geq 0$.

We note from the table that $color{#4257b2}f(x) geq 0$ at the intervals $color{#4257b2}-2 geq xgeq -1$ or $color{#4257b2}xgeq 1$, so the solution of the inequality $color{#4257b2}(x+3)(x-2)(x+1)geq 0$ is $color{#c34632}x in [-2, -1] {color{Black}text{or}} x in [3, infty)$.

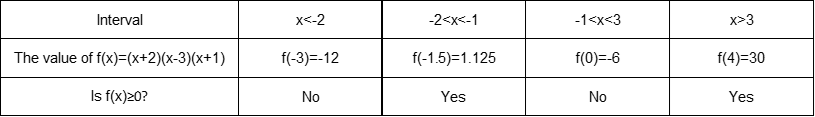
(b) We would like to solve the inequality $color{#4257b2}-2(x-2)(x-4)(x+3) < 0$ using the number line strategy. First, we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
-2(x-2)(x-4)(x+3) < 0
$$

$$
-2(x-2)(x-4)(x+3)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x-2=0, x-4=0 text{or} x+3=0
$$

$$
x=2, x=4 text{or} x=-3
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

Now we find that the roots are $color{#4257b2}-3, 2$ and $color{#4257b2}4$, so these numbers will divide the domain to four intervals $color{#4257b2}x<-3, -4<x<2, 2<x4$ and the following number line shows these intervals

Now we have four intervals and we know that our inequality is
$color{#4257b2}-2(x-2)(x-4)(x+3) < 0$, so we can let $color{#4257b2}f(x)=-2(x-2)(x-4)(x+3)$ and then create a table to consider the sign of the function $color{#4257b2}f(x)$ at each interval to know the intervals where this function will be negative to verify our inequality $color{#4257b2}-2(x-2)(x-4)(x+3) < 0$.

We note from the table that $color{#4257b2}f(x) < 0$ at the intervals $color{#4257b2}-3 < x 4$, so the solution of the inequality $color{#4257b2}-2(x-2)(x-4)(x+3) < 0$ is $color{#c34632}x in (-3, 2) {color{Black}text{or}} x in (4, infty)$.

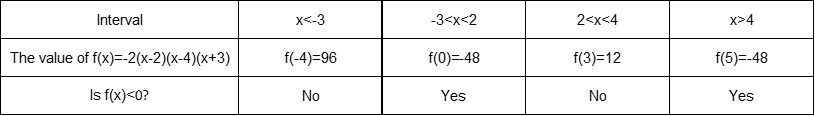
(c) We would like to solve the inequality $color{#4257b2}(x-3)(5x+2)(4x-3) < 0$ using the number line strategy. First, we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
(x-3)(5x+2)(4x-3) < 0
$$

$$
(x-3)(5x+2)(4x-3)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x-3=0, 5x+2=0 text{or} 4x-3=0
$$

$$
x=3, 5x=-2 text{or} 4x=3
$$

$$
x=3, x=-dfrac{2}{5}=-0.4 text{or} x=dfrac{3}{4}=0.75
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

Now we find that the roots are $color{#4257b2}-0.4, 0.75$ and $color{#4257b2}3$, so these numbers will divide the domain to four intervals $color{#4257b2}x<-0.4, -0.4<x<0.75, 0.75<x3$ and the following number line shows these intervals

Now we have four intervals and we know that our inequality is
$color{#4257b2}(x-3)(5x+2)(4x-3) < 0$, so we can let $color{#4257b2}f(x)=(x-3)(5x+2)(4x-3)$ and then create a table to consider the sign of the function $color{#4257b2}f(x)$ at each interval to know the intervals where this function will be negative to verify our inequality $color{#4257b2}(x-3)(5x+2)(4x-3) < 0$.

We note from the table that $color{#4257b2}f(x) < 0$ at the intervals $color{#4257b2}x < -0.4$ or $color{#4257b2}0.75 < x < 3$, so the solution of the inequality $color{#4257b2}(x-3)(5x+2)(4x-3) < 0$ is $color{#c34632}x in (-infty, -0.4) {color{Black}text{or}} x in (0.75, 3)$.

(d) We would like to solve the inequality $color{#4257b2}(x-5)(4x+1)(2x-5)geq 0$ using the number line strategy. First, we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
(x-5)(4x+1)(2x-5)geq 0
$$

$$
(x-5)(4x+1)(2x-5)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x-5=0, 4x+1=0 text{or} 2x-5=0
$$

$$
x=5, 4x=-1 text{or} 2x=5
$$

$$
x=5, x=-dfrac{1}{4}=-0.25 text{or} x=dfrac{5}{2}=2.5
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

Now we find that the roots are $color{#4257b2}-0.25, 2.5$ and $color{#4257b2}5$, so these numbers will divide the domain to four intervals $color{#4257b2}x<-0.25, -0.25<x<2.5, 2.5<x5$ and the following number line shows these intervals

Now we have four intervals and we know that our inequality is
$color{#4257b2}(x-5)(4x+1)(2x-5) geq 0$, so we can let $color{#4257b2}f(x)=(x-5)(4x+1)(2x-5)$ and then create a table to consider the sign of the function $color{#4257b2}f(x)$ at each interval to know the intervals where this function will be positive or equals zero to verify our inequality $color{#4257b2}(x-5)(4x+1)(2x-5) geq 0$.

We note from the table that $color{#4257b2}f(x) geq 0$ at the intervals $color{#4257b2}-0.25 geq xgeq 2.5$ or $color{#4257b2}xgeq 5$, so the solution of the inequality $color{#4257b2}(x-5)(4x+1)(2x-5)geq 0$ is $color{#c34632}x in [-0.25, 2.5] {color{Black}text{or}} x in [5, infty)$.

Large{$text{color{Brown}(a) $x in [-2, -1] {color{Black}text{or}} x in [3, infty)$
\
\
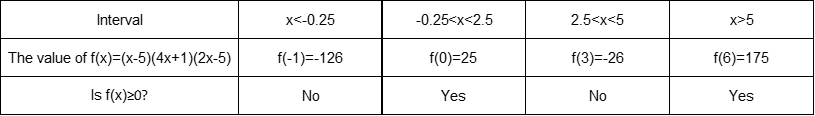
(b) $x in (-3, 2) {color{Black}text{or}} x in (4, infty)$
\
\
(c) $x in (-infty, -0.4) {color{Black}text{or}} x in (0.75, 3)$
\
\
(d) $x in [-0.25, 2.5] {color{Black}text{or}} x in [5, infty)$}$

(a) We would like to determine where $color{#4257b2}f(x)leq 0$ in the given graph. First, to know the intervals where $color{#4257b2}f(x)leq 0$, we need to find the intervals where the graph lies down or equal the x-axis because in this case the value of the function will be negative or zero and this verifies the inequality $color{#4257b2}f(x)leq 0$.

We note from the graph that the function lies down or equal the x-axis at three intervals $color{#4257b2}x leq -5, -2 leq xleq 0 text{and} x geq 3$, so the solution of the inequality $color{#4257b2}f(x)leq 0$ is $color{#c34632}x in (-infty, -5], x in [-2, 0] {color{Black}text{or}} x in [3, infty)$.

(b) We would like to determine where $color{#4257b2}f(x)leq 0$ in the given graph. First, to know the intervals where $color{#4257b2}f(x)leq 0$, we need to find the intervals where the graph lies down or equal the x-axis because in this case the value of the function will be negative or zero and this verifies the inequality $color{#4257b2}f(x)leq 0$.

We note from the graph that the function doesn’t lie down the x-axis but it just touches the x-axis at the point $color{#4257b2}(1, 0)$, so the solution of the inequality $color{#4257b2}f(x)leq 0$ is $color{#c34632}x =0$.

(c) We would like to determine where $color{#4257b2}f(x)leq 0$ in the given graph. First, to know the intervals where $color{#4257b2}f(x)leq 0$, we need to find the intervals where the graph lies down or equal the x-axis because in this case the value of the function will be negative or zero and this verifies the inequality $color{#4257b2}f(x)leq 0$.

We note from the graph that the function lies down or equal the x-axis at two intervals $color{#4257b2}-7 leq x leq -3 text{and} 0leq x leq 4$, so the solution of the inequality $color{#4257b2}f(x)leq 0$ is $color{#c34632}x in [-7, -3] {color{Black}text{or}} x in [0, 4]$.

(d) We would like to determine where $color{#4257b2}f(x)leq 0$ in the given graph. First, to know the intervals where $color{#4257b2}f(x)leq 0$, we need to find the intervals where the graph lies down or equal the x-axis because in this case the value of the function will be negative or zero and this verifies the inequality $color{#4257b2}f(x)leq 0$.

We note from the graph that the function lies down or equal the x-axis at two intervals $color{#4257b2}x leq -4 text{and} 2leq x leq 7$, so the solution of the inequality $color{#4257b2}f(x)leq 0$ is $color{#c34632}x in (-infty, -4] {color{Black}text{or}} x in [2, 7]$.

Large{$text{color{Brown}(a) $x in (-infty, -5], x in [-2, 0] {color{Black}text{or}} x in [3, infty)$
\
\
(b) $x=0$
\
\
(c) $x in [-7, -3] {color{Black}text{or}} x in [0, 4]$
\
\
(d) $x in (-infty, -4] {color{Black}text{or}} x in [2, 7]$}$

We would like to solve the inequality $color{#4257b2}f(x) > g(x)$ using the factor table strategy if we know that $color{#4257b2}f(x)=2x^{3}-x^{2}+3x+10$ and $color{#4257b2}g(x)=x^{3}+3x^{2}+2x+4$. First, we will substitute the values of the each function in the inequality $color{#4257b2}f(x) > g(x)$ and then solve it.

$$
f(x) > g(x)
$$

$$
2x^{3}-x^{2}+3x+10 > x^{3}+3x^{2}+2x+4
$$

Now we can subtract $color{#4257b2}x^{3}+3x^{2}+2x+4$ from each side to make the right side equals zero.

$$
2x^{3}-x^{2}+3x+10-(x^{3}+3x^{2}+2x+4) > 0
$$

$$
x^{3}-4x^{2}+x+6 > 0 (1)
$$

Now we have a cubic function in the left side, so we can let
$color{#4257b2}f(x)=x^{3}-4x^{2}+x+6$ and then we can use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=x^{3}-4x^{2}+x+6$, so $color{#4257b2}p=6$ and $color{#4257b2}q=1$. As a result the root could be of the form $color{#4257b2}dfrac{6}{1}=6$ and the factors of it are $color{#4257b2}pm 1, pm 2, pm 3, pm 6$. Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=x^{3}-4x^{2}+x+6
$$

$$
f(1)=(1)^{3}-4(1)^{2}+(1)+6=4
$$

$$
f(-1)=(-1)^{3}-4(-1)^{2}+(-1)+6=0
$$

By the factor theorem, $color{#4257b2}(x+1)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x+1)$ to find the remaining factors.

$$
polylongdiv{x^{3}-4x^{2}+x+6}{x+1}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x+1right)left(x^{2}-5x+6right)$. Now the next step is to factor the quadratic function $color{#4257b2}x^{2}-5x+6$.

$$
f(x)=left(x+1right)left(x^{2}-5x+6right)
$$

$$
f(x)=left(x+1right)left(x-2right)left(x-3right)
$$

Now we found the factors of the function $color{#4257b2}f(x)=x^{3}-4x^{2}+x+6$, so we can substitute in our inequality (1).

$$
left(x+1right)left(x-2right)left(x-3right) > 0
$$

Now we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
left(x+1right)left(x-2right)left(x-3right)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x+1=0, x-2=0 text{or} x-3=0
$$

$$
x=-1, x=2 text{or} x=3
$$

Now we find that the roots are $color{#4257b2}-1, 2$ and $color{#4257b2}3$, so these numbers will divide the domain to four intervals $color{#4257b2}x<-1, -1<x<2, 2<x3$.

Now we have three factors of the inequality $color{#4257b2}(x+1), (x-2)$ and $color{#4257b2}(x-3)$ and we have four intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}(x+1)(x-2)(x-3)$ will be positive to verify our inequality $color{#4257b2}(x+1)(x-2)(x-3) > 0$.

We note from the table that the product $color{#4257b2}(x+1)(x-2)(x-3)$ is positive at the intervals $color{#4257b2}-1 < x 3$, so the solution of the inequality $color{#4257b2}x^{3}f(x) > g(x)$ is $color{#c34632}x in (-1, 2) {color{Black}text{or}} x in (3, infty)$.

$$
color{Brown}x in (-1, 2) {color{Black}text{or}} x in (3, infty)
$$

We would like to solve the inequality $color{#4257b2}x^{3}-7x^{2}+4x+12 > x^{2}-4x-9$ using the graphing calculator. First, we can graph the cubic function of the left side $color{#4257b2}f(x)=x^{3}-7x^{2}+4x+12$ and graph the quadratic function of the right side $color{#4257b2}g(x)=x^{2}-4x-9$ on the same plane and then find the intervals where the graph of the left side will lie above the graph of the right side.

The two functions intersects at the points $color{#4257b2}(-1.14, -3.14), (3, -12)$ and $color{#4257b2}(6.14, 4.14)$. Now we can see from the two graphs that the graph of the function $color{#4257b2}f(x)=x^{3}-7x^{2}+4x+12$ lies above the graph $color{#4257b2}g(x)=x^{2}-4x-9$ in two cases: the first case for $color{#4257b2}-1.14 < x 6.14$, so the solutions of the inequality $color{#4257b2}x^{3}-7x^{2}+4x+12 > x^{2}-4x-9$ is $color{#c34632}x in (-1.14, 3) {color{Black}text{or}} x in (6.14, infty)$.

Large{$text{color{Brown}$x in (-1.14, 3) {color{Black}text{or}} x in (6.14, infty)$}$

(a) We would like to determine where $color{#4257b2}f(x) > 0$ in the given graph. First, to know the intervals where $color{#4257b2}f(x) > 0$, we need to find the intervals where the graph lies above the x-axis because in this case the value of the function will be positive and this verifies the inequality $color{#4257b2}f(x) > 0$.

We note from the graph that the function lies above the x-axis at two intervals $color{#4257b2}-1 < x 4$, so the solution of the inequality $color{#4257b2}f(x) > 0$ is $color{#c34632}x in (-1, 2) {color{Black}text{or}} x in (4, infty)$.

(b) We would like to determine where $color{#4257b2}f(x) > 0$ in the given graph. First, to know the intervals where $color{#4257b2}f(x) > 0$, we need to find the intervals where the graph lies above the x-axis because in this case the value of the function will be positive and this verifies the inequality $color{#4257b2}f(x) > 0$.

We note from the graph that the function lies above the x-axis at two intervals $color{#4257b2}-2 < x < 2 text{and} x 0$ is $color{#c34632}x in (-2, 2) {color{Black}text{or}} x in (2, infty)$.

Note that the value of $color{#4257b2}x=2$ doesn’t verify the inequality $color{#4257b2}f(x) > 0$ because at $color{#4257b2}x=2$ the value of the function $color{#4257b2}f(x)$ equals zero, so we didn’t write it in our solution.

(c) We would like to determine where $color{#4257b2}f(x) > 0$ in the given graph. First, to know the intervals where $color{#4257b2}f(x) > 0$, we need to find the intervals where the graph lies above the x-axis because in this case the value of the function will be positive and this verifies the inequality $color{#4257b2}f(x) > 0$.

We note from the graph that the function lies above the x-axis at two intervals $color{#4257b2} x < -2 text{and} 0 < x 0$ is $color{#c34632}x in (-infty, -2) {color{Black}text{or}} x in (0, 1)$.

(d) We would like to determine where $color{#4257b2}f(x) > 0$ in the given graph. First, to know the intervals where $color{#4257b2}f(x) > 0$, we need to find the intervals where the graph lies above the x-axis because in this case the value of the function will be positive and this verifies the inequality $color{#4257b2}f(x) > 0$.

We note from the graph that the function lies above the x-axis at all real numbers except at $color{#4257b2}x=2$ where in this case the value of $color{#4257b2}f(x)$ equals zero, so the solution of the inequality $color{#4257b2}f(x) > 0$ is $color{#c34632}x in (-infty, 2) {color{Black}text{or}} x in (2, infty)$.

Note that the value of $color{#4257b2}x=2$ doesn’t verify the inequality $color{#4257b2}f(x) > 0$ because at $color{#4257b2}x=2$ the value of the function $color{#4257b2}f(x)$ equals zero, so we didn’t write it in our solution.

Large{$text{color{Brown}(a) $x in (-1, 2) {color{Black}text{or}} x in (4, infty)$
\
\
(b) $x in (-2, 2) {color{Black}text{or}} x in (2, infty)$
\
\
(c) $x in (-infty, -2) {color{Black}text{or}} x in (0, 1)$
\
\
(d) $x in (-infty, 2) {color{Black}text{or}} x in (2, infty)$}$

(a) We would like to solve the inequality $color{#4257b2}(x-1)(x+1)>0$. First, we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
(x-1)(x+1)>0
$$

$$
(x-1)(x+1)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x-1=0 text{or} x+1=0
$$

$$
x=1 text{or} x=-1
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

Now we find that the roots are $color{#4257b2}-1$ and $color{#4257b2}1$, so these numbers will divide the domain to three intervals $color{#4257b2}x<-1, -1<x1$ and the following number line shows these intervals

Now we have two factors of the inequality $color{#4257b2}(x-1)$ and $color{#4257b2}(x+1)$ and we have three intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}(x-1)(x+1)$ will be positive to verify our inequality $color{#4257b2}(x-1)(x+1)>0$.

We note from the table that the product $color{#4257b2}(x-1)(x+1)$ is positive at the intervals $color{#4257b2}x1$, so the solution of the inequality $color{#4257b2}(x-1)(x+1)>0$ is $color{#c34632}x in (-infty, -1) {color{Black}text{or}} x in (1, infty)$.

(b) We would like to solve the inequality $color{#4257b2}(x+3)(x-4)<0$. First, we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
(x+3)(x-4)<0
$$

$$
(x+3)(x-4)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x+3=0 text{or} x-4=0
$$

$$
x=-3 text{or} x=4
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

Now we find that the roots are $color{#4257b2}-3$ and $color{#4257b2}4$, so these numbers will divide the domain to three intervals $color{#4257b2}x<-3, -3<x4$ and the following number line shows these intervals

Now we have two factors of the inequality $color{#4257b2}(x+3)$ and $color{#4257b2}(x-4)$ and we have three intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}(x+3)(x-4)$ will be negative to verify our inequality $color{#4257b2}(x+3)(x-4)<0$.

We note from the table that the product $color{#4257b2}(x+3)(x-4)$ is negative at the interval $color{#4257b2}-3<x0$ is $color{#c34632}x in (-3, 4)$.

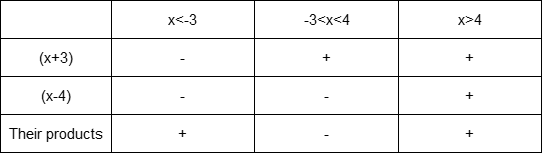
(c) We would like to solve the inequality $color{#4257b2}(2x+1)(x-5) geq 0$. First, we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
(2x+1)(x-5) geq 0
$$

$$
(2x+1)(x-5)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
2x+1=0 text{or} x-5=0
$$

$$
x=-dfrac{1}{2} text{or} x=5
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

Now we find that the roots are $color{#4257b2}-0.5$ and $color{#4257b2}5$, so these numbers will divide the domain to three intervals $color{#4257b2}x<-0.5, -0.5<x5$ and the following number line shows these intervals

Now we have two factors of the inequality $color{#4257b2}(2x+1)$ and $color{#4257b2}(x-5)$ and we have three intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}(2x+1)(x-5)$ will be positive or equals zero to verify our inequality $color{#4257b2}(2x+1)(x-5)geq 0$.

We note from the table that the product $color{#4257b2}(2x+1)(x-5)$ is positive or equals zero at the intervals $color{#4257b2}xleq-0.5$ or $color{#4257b2}x geq 5$, so the solution of the inequality $color{#4257b2}(2x+1)(x-5) geq 0$ is $color{#c34632}x in (-infty, -0.5] {color{Black}text{or}} x in [5, infty)$.

(d) We would like to solve the inequality $color{#4257b2}-3x(x+7)(x-2)<0$. First, we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
-3x(x+7)(x-2)<0
$$

$$
-3x(x+7)(x-2)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
-3x=0, x+7=0 text{or} x-2=0
$$

$$
x=0, x=-7 text{or} x=2
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

Now we find that the roots are $color{#4257b2}-7, 0$ and $color{#4257b2}2$, so these numbers will divide the domain to four intervals $color{#4257b2}x<-7, -7<x<0, 0<x2$ and the following number line shows these intervals

Now we have three factors of the inequality $color{#4257b2}-3x, (x+7)$ and $color{#4257b2}(x-2)$ and we have four intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}-3x(x+7)(x-2)$ will be negative to verify our inequality $color{#4257b2}-3x(x+7)(x-2)<0$.

We note from the table that the product $color{#4257b2}-3x(x+7)(x-2)$ is negative at the intervals $color{#4257b2}-7 2$, so the solution of the inequality $color{#4257b2}-3x(x+7)(x-2)<0$ is $color{#c34632}x in (-7, 0) {color{Black}text{or}} x in (2, infty)$.

(e) We would like to solve the inequality $color{#4257b2}(x-3)(x+1)+(x-3)(x+2) geq 0$. First, we note that the two terms of the left side each of them contains the factor $color{#4257b2}(x-3)$, so we can take it as a common factor.

$$
(x-3)(x+1)+(x-3)(x+2) geq 0
$$

$$
(x-3)(x+1+x+2) geq 0
$$

$$
(x-3)(2x+3) geq 0
$$

Now we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
(x-3)(2x+3)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x-3=0 text{or} 2x+3=0
$$

$$
x=3 text{or} x=-dfrac{3}{2}
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

Now we find that the roots are $color{#4257b2}-1.5$ and $color{#4257b2}3$, so these numbers will divide the domain to three intervals $color{#4257b2}x<-1.5, -1.5<x3$ and the following number line shows these intervals

Now we have two factors of the inequality $color{#4257b2}(x-3)$ and $color{#4257b2}(2x+3)$ and we have three intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}(x-3)(2x+3)$ will be positive or equals zero to verify our inequality $color{#4257b2}(x-3)(2x+3)geq 0$.

We note from the table that the product $color{#4257b2}(x-3)(2x+3)$ is positive or equals zero at the intervals $color{#4257b2}xleq-1.5$ or $color{#4257b2}x geq 3$, so the solution of the inequality $color{#4257b2}(x-3)(2x+3) geq 0$ is $color{#c34632}x in (-infty, -1.5] {color{Black}text{or}} x in [3, infty)$.

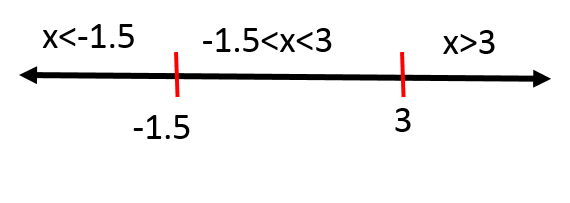
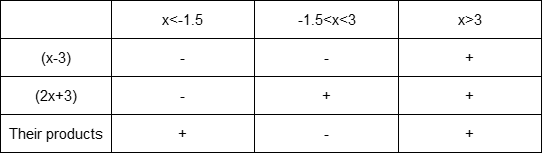
(f) We would like to solve the inequality $color{#4257b2}2x(x+4)-3(x+4) leq 0$. First, we note that the two terms of the left side each of them contains the factor $color{#4257b2}(x+4)$, so we can take it as a common factor.

$$
2x(x+4)-3(x+4) leq 0
$$

$$
(x+4)(2x-3) leq 0
$$

Now we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
(x+4)(2x-3)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x+4=0 text{or} 2x-3=0
$$

$$
x=-4 text{or} x=dfrac{3}{2}
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

Now we find that the roots are $color{#4257b2}-4$ and $color{#4257b2}1.5$, so these numbers will divide the domain to three intervals $color{#4257b2}x<-4, -4<x1.5$ and the following number line shows these intervals

Now we have two factors of the inequality $color{#4257b2}(x+4)$ and $color{#4257b2}(2x-3)$ and we have three intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}(x+4)(2x-3)$ will be negative or equals zero to verify our inequality $color{#4257b2}(x+4)(2x-3)leq 0$.

We note from the table that the product $color{#4257b2}(x+4)(2x-3)$ is negative or equals zero at the interval $color{#4257b2}-4 leq x leq 1.5$, so the solution of the inequality $color{#4257b2}(x+4)(2x-3) leq 0$ is $color{#c34632}x in [-4, 1.5]$.

Large{$text{color{Brown}(a) $x in (-infty, -1) {color{Black}text{or}} x in (1, infty)$
\
\
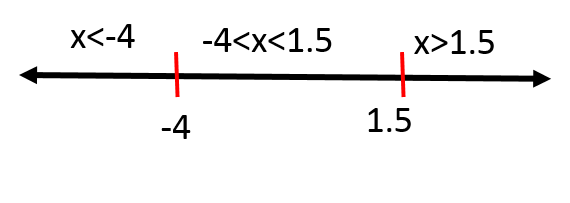
(b) $x in (-3, 4)$
\
\
(c) $x in (-infty, -0.5] {color{Black}text{or}} x in [5, infty)$
\
\
(d) $x in (-7, 0) {color{Black}text{or}} x in (2, infty)$
\
\
(e) $x in (-infty, -1.5] {color{Black}text{or}} x in [3, infty)$
\
\
(f) $x in [-4, -1.5]$}$

(a) We would like to solve the inequality $color{#4257b2}x^{2}-6x+9geq 16$. First, we can subtract $color{#4257b2}16$ from each side to make the right side equals zero.

$$
x^{2}-6x+9geq 16
$$

$$
x^{2}-6x+9-16geq 0
$$

$$
x^{2}-6x-7geq 0
$$

Now we have a quadratic function in the left side, so we can factor it to know the factors of this function.

$$
(x+1)(x-7)geq 0
$$

Now we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
(x+1)(x-7)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x+1=0 text{or} x-7=0
$$

$$
x=-1 text{or} x=7
$$

Note that we converted our inequality to an equation to find the roots of this equation because these roots will divide the domain to numbers of intervals and then check the sign of each interval.

Now we find that the roots are $color{#4257b2}-1$ and $color{#4257b2}7$, so these numbers will divide the domain to three intervals $color{#4257b2}x<-1, -1<x7$ and the following number line shows these intervals

Now we have two factors of the inequality $color{#4257b2}(x+1)$ and $color{#4257b2}(x-7)$ and we have three intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}(x+1)(x-7)$ will be positive to verify our inequality $color{#4257b2}(x+1)(x-7)geq 0$.

We note from the table that the product $color{#4257b2}(x+1)(x-7)$ is positive or equals zero at the intervals $color{#4257b2}xleq -1$ or $color{#4257b2}xgeq 7$, so the solution of the inequality $color{#4257b2}x^{2}-6x+9 geq 16$ is $color{#c34632}x in (-infty, -1] {color{Black}text{or}} x in [7, infty)$.

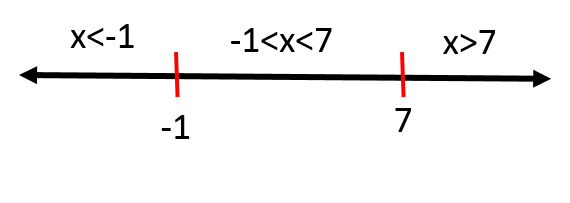
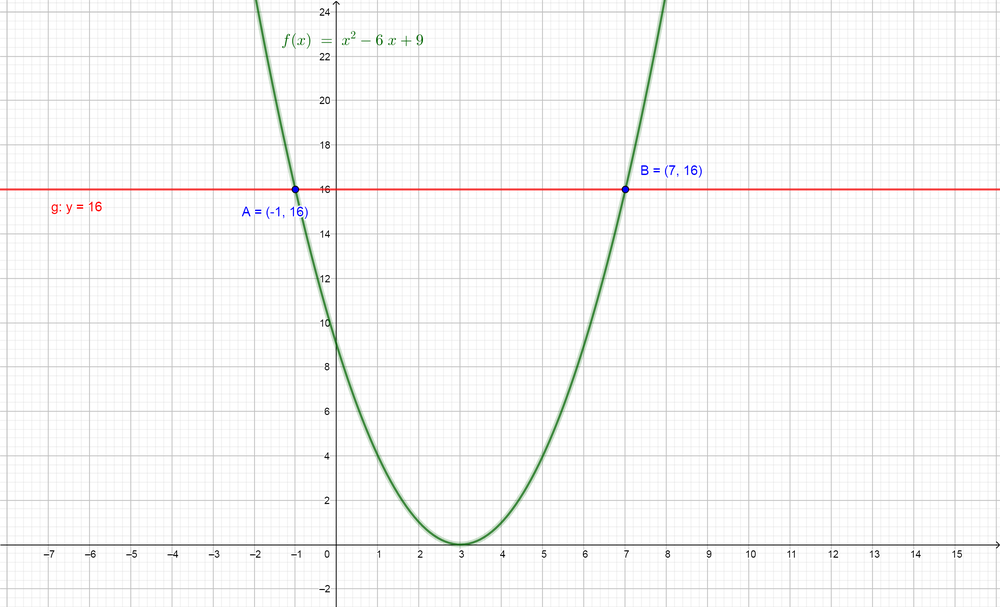
Now we need to use the graph to confirm our solution for the inequality $color{#4257b2}x^{2}-6x+9 geq 16$, so we can graph the function of the left side
$color{#4257b2}f(x)=x^{2}-6x+9$ and graph the line of the right side $color{#4257b2}y=16$ on the same plane and then find the intervals where the graph of the left side will lie above the line of the right side.

We note from the two graphs that the graph of the function $color{#4257b2}f(x)=x^{2}-6x+9$ lies above or equals the line $color{#4257b2}y=16$ in two cases: the first case for $color{#4257b2}x leq -1$ and the second case for $color{#4257b2}x geq 7$, so the solutions of our inequality will be at these intervals and this confirm our solution $color{#c34632}x in (-infty, -1] {color{Black}text{or}} x in [7, infty)$.

(b) We would like to solve the inequality $color{#4257b2}x^{4}-8x < 0$. First, we note that the two terms in the left side contains $color{#4257b2}x$, so we can take it as a common factor.

$$
x^{4}-8x < 0
$$

$$
x(x^{3}-8) < 0
$$

Now we have a cubic function in the left side on the form $color{#4257b2}x^{3}-a^{3}$, so we can factor it to know the factors of this function where
$color{#4257b2}x^{3}-a^{3}=(x-a)(x^{2}+a x+a^{2})$.

$$
x(x-2)(x^{2}+2x+4) < 0
$$

Now we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
x(x-2)(x^{2}+2x+4)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x=0, x-2=0 text{or} x^{2}+2x+4=0
$$

But we note that the factor $color{#4257b2}x^{2}+2x+4$ is positive for all real numbers, so the factor $color{#4257b2}x^{2}+2x+4$ has no zeros.

$$
x=0 text{or} x=2
$$

Now we find that the roots are $color{#4257b2}0$ and $color{#4257b2}2$, so these numbers will divide the domain to three intervals $color{#4257b2}x<0, 0<x2$ and the following number line shows these intervals

Now we have three factors of the inequality $color{#4257b2}x, (x-2)$ and $color{#4257b2}(x^{2}+2x+4)$ and we have three intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}x(x-2)(x^{2}+2x+4)$ will be negative to verify our inequality $color{#4257b2}x(x-2)(x^{2}+2x+4) < 0$.

We note from the table that the product $color{#4257b2}x(x-2)(x^{2}+2x+4)$ is negative at the interval $color{#4257b2} 0< x < 2$, so the solution of the inequality $color{#4257b2}x^{4}-8x < 0$ is $color{#c34632}x in (0, 2)$.

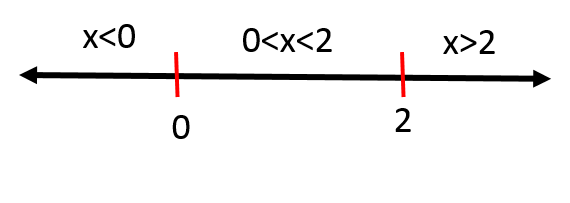
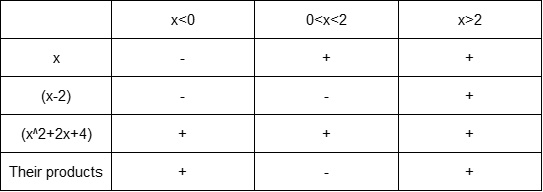
Now we need to use the graph to confirm our solution for the inequality $color{#4257b2}x^{4}-8x < 0$, so we can graph the function of the left side
$color{#4257b2}f(x)=x^{4}-8x$ and then find the intervals where the graph of the left side will lie down the x-axis because the right side of the inequality is zero..

We note from the two graphs that the graph of the function $color{#4257b2}f(x)=x^{4}-8x$ lies down the x-axis in the interval $color{#4257b2}0 < x < 2$, so the solutions of our inequality will be at this interval and this confirms our solution $color{#c34632}x in (0, 2)$.

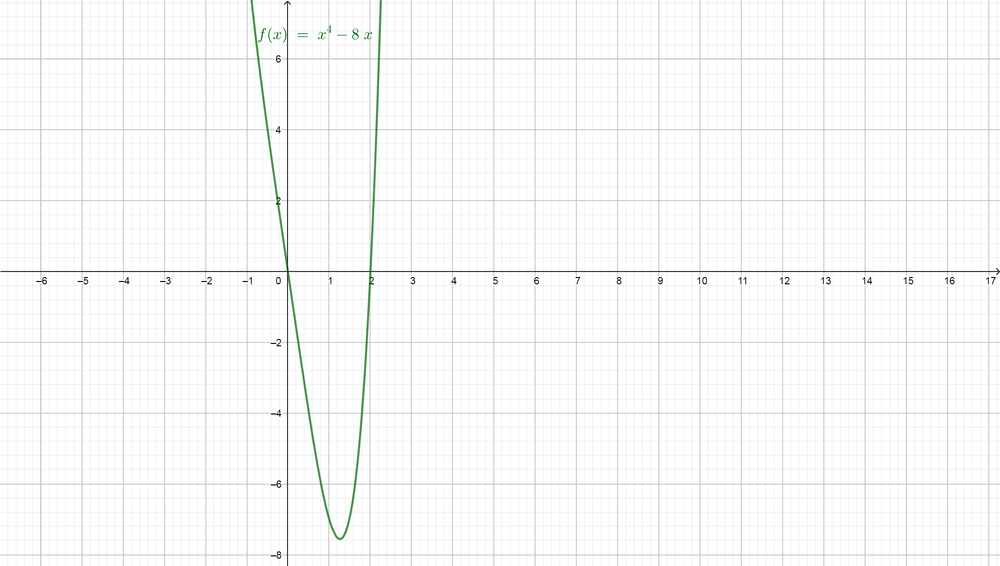
(c) We would like to solve the inequality $color{#4257b2}x^{3}+4x^{2}+x leq 6$. First, we can subtract $color{#4257b2}6$ from each side to make the right side equals zero.

$$
x^{3}+4x^{2}+x leq 6
$$

$$
x^{3}+4x^{2}+x-6 leq 0 (1)
$$
.

Now we have a cubic function in the left side, so we can let
$color{#4257b2}f(x)=x^{3}+4x^{2}+x-6$ and then we can use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=x^{3}+4x^{2}+x-6$, so $color{#4257b2}p=6$ and $color{#4257b2}q=1$. As a result the root could be of the form $color{#4257b2}dfrac{6}{1}=6$ and the factors of it are $color{#4257b2}pm 1, pm 2, pm 3, pm 6$. Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=x^{3}+4x^{2}+x-6
$$

$$
f(1)=(1)^{3}+4(1)^{2}+(1)-6=0
$$

By the factor theorem, $color{#4257b2}(x-1)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x-1)$ to find the remaining factors.

$$
polylongdiv{x^{3}+4x^{2}+x-6}{x-1}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x-1right)left(x^{2}+5x+6right)$. Now the next step is to factor the quadratic function $color{#4257b2}x^{2}+5x+6$.

$$
f(x)=left(x-1right)left(x^{2}+5x+6right)
$$

$$
f(x)=left(x-1right)left(x+2right)left(x+3right)
$$

Now we found the factors of the function $color{#4257b2}f(x)=x^{3}-6x^{2}-x+30$, so we can substitute in our inequality (1).

$$
left(x-1right)left(x+2right)left(x+3right)leq 0
$$

Now we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
left(x-1right)left(x+2right)left(x+3right)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x-1=0, x+2=0 text{or} x+3=0
$$

$$
x=1, x=-2 text{or} x=-3
$$

Now we find that the roots are $color{#4257b2}-3, -2$ and $color{#4257b2}1$, so these numbers will divide the domain to four intervals $color{#4257b2}x<-3, -3<x<-2, -2<x1$ and the following number line shows these intervals

Now we have three factors of the inequality $color{#4257b2}(x-1), (x+2)$ and $color{#4257b2}(x+3)$ and we have four intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}(x-1)(x+2)(x+3)$ will be negative or equals zero to verify our inequality $color{#4257b2}(x-1)(x+2)(x+3) leq 0$.

We note from the table that the product $color{#4257b2}(x-1)(x+2)(x+3)$ is negative or equals zero at the intervals $color{#4257b2}xleq -3$ or $color{#4257b2}-2 leq x leq 1$, so the solution of the inequality $color{#4257b2}x^{3}+4x+x leq 6$ is $color{#c34632}x in (-infty, -3] {color{Black}text{or}} x in [-2, 1]$.

Now we need to use the graph to confirm our solution for the inequality $color{#4257b2}x^{3}+4x+x leq 6$, so we can graph the function of the left side
$color{#4257b2}f(x)=x^{3}+4x+x$ and graph the line of the right side $color{#4257b2}y=6$ on the same plane and then find the intervals where the graph of the left side will lie down the line of the right side.

We note from the two graphs that the graph of the function
$color{#4257b2}f(x)=x^{3}+4x^{2}+x$ lies down or equals the line $color{#4257b2}y=6$ in two cases: the first case for $color{#4257b2}x leq -3$ and the second case for $color{#4257b2}-2 leq x leq 1$, so the solutions of our inequality will be at these intervals and this confirm our solution $color{#c34632}x in (-infty, -3] {color{Black}text{or}} x in [-2, 1]$.

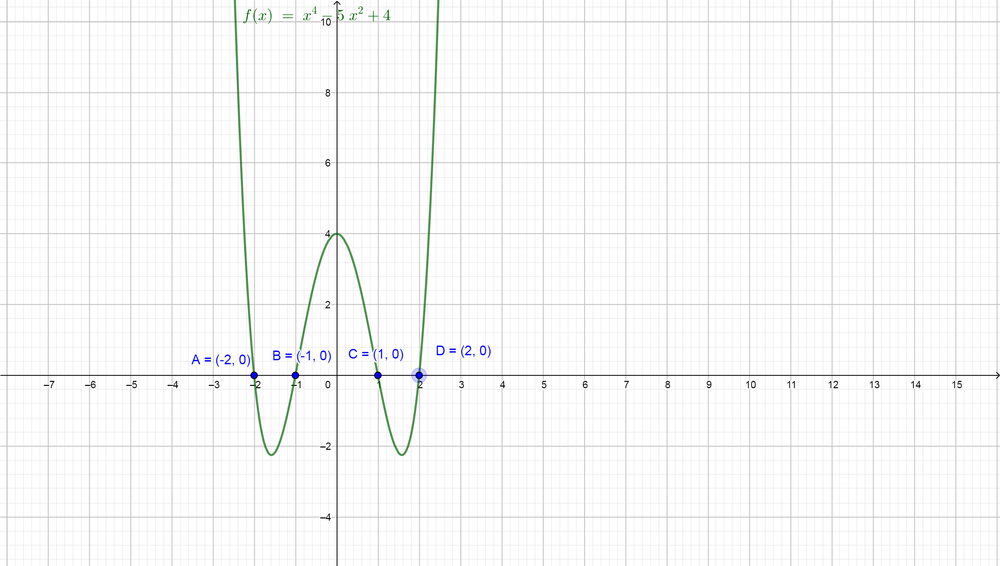
(d) We would like to solve the inequality $color{#4257b2}x^{4}-5x^{2}+4 > 0$. First, that we have a function of the fourth degree in the left side, so we can factor it to know the factors of this function.

$$
x^{4}-5x^{2}+4 > 0
$$

$$
(x^{2}-1)(x^{2}-4) > 0
$$

Now we note that we have two factors each of them is a quadratic function on the form $color{#4257b2}x^{2}-a^{2}$, so we can factor each of them where $color{#4257b2}x^{2}-a^{2}=(x+a)(x-a)$.

$$
(x+1)(x-1)(x+2)(x-2) > 0
$$

Now we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
(x+1)(x-1)(x+2)(x-2)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x+1=0, x-1=0, x+2=0 text{or} x-2=0
$$

$$
x=-1, x=1, x=-2 text{or} x=2
$$

Now we find that the roots are $color{#4257b2}-2, -1, 1$ and $color{#4257b2}2$, so these numbers will divide the domain to five intervals $color{#4257b2}x<-2, -2<x<-1, -1<x<1, 1<x2$ and the following number line shows these intervals

Now we have four factors of the inequality $color{#4257b2}(x+1), (x-1), (x+2)$ and $color{#4257b2}(x-2)$ and we have five intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}(x+1)(x-1)(x+2)(x-2)$ will be positive to verify our inequality $color{#4257b2}(x+1)(x-1)(x+2)(x-2) < 0$.

We note from the table that the product $color{#4257b2}(x+1)(x-1)(x+2)(x-2)$ is positive at the intervals $color{#4257b2} x < -2, -1<x2$, so the solution of the inequality $color{#4257b2}x^{4}-5x^{2}+4 > 0$ is $color{#c34632}x in (-infty, -2), x in (-1, 1) {color{Black}text{or}} x in (2, infty)$.

Now we need to use the graph to confirm our solution for the inequality $color{#4257b2}x^{4}-5x^{2}+4 > 0$, so we can graph the function of the left side
$color{#4257b2}f(x)=x^{4}-5x^{2}+4$ and then find the intervals where the graph of the left side will lie above the x-axis because the right side of the inequality is zero.

We note from the two graphs that the graph of the function $color{#4257b2}f(x)=x^{4}-5x^{2}+4$ lies above the x-axis in the intervals $color{#4257b2} x < -2, -1<x2$, so the solutions of our inequality will be at this interval and this confirms our solution $color{#c34632}x in (-infty, -2), x in (-1, 1) {color{Black}text{or}} x in (2, infty)$.

(e) We would like to solve the inequality $color{#4257b2}3x^{3}-3x^{2}-2x leq 2x^{3}-x^{2}+x$. First, we can subtract $color{#4257b2}2x^{3}-x^{2}+x$ from each side to make the right side equals zero.

$$
3x^{3}-3x^{2}-2x- 2x^{3}+x^{2}-x leq 0
$$

$$
x^{3}-2x^{2}-3x leq 0
$$

Now we note that all terms of the left side contain $color{#4257b2}x$, so we can take it as a common factor.

$$
x(x^{2}-2x-3) leq 0
$$

Now the next step is to factor the quadratic function $color{#4257b2}x^{2}-2x-3$.

$$
xleft(x-3right)left(x+1right) leq 0
$$

Now we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
xleft(x-3right)left(x+1right)=0
$$

$$
x=0, x-3=0 text{or} x+1=0
$$

$$
x=0, x=3 text{or} x=-1
$$

Now we find that the roots are $color{#4257b2}-1, 0$ and $color{#4257b2}3$, so these numbers will divide the domain to four intervals $color{#4257b2}x<-1, -1<x<0, 0<x3$ and the following number line shows these intervals

Now we have three factors of the inequality $color{#4257b2}x, (x-3)$ and $color{#4257b2}(x+1)$ and we have four intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}x(x-3)(x+1)$ will be negative or equals zero to verify our inequality $color{#4257b2}x(x-3)(x+1) leq 0$.

We note from the table that the product $color{#4257b2}x(x-3)(x+1)$ is negative or equals zero at the intervals $color{#4257b2}xleq -1$ or $color{#4257b2}0 leq x leq 3$, so the solution of the inequality $color{#4257b2}3x^{3}-3x^{2}-2x leq 2x^{3}-x^{2}+x$ is $color{#c34632}x in (-infty, -1] {color{Black}text{or}} x in [0, 3]$.

Now we need to use the graph to confirm our solution for the inequality $color{#4257b2}3x^{3}-3x^{2}-2x leq 2x^{3}-x^{2}+x$, so we can graph the function of the left side
$color{#4257b2}f(x)=3x^{3}-3x^{2}-2x$ and graph the function of the right side
$color{#4257b2}g(x)=2x^{3}-x^{2}+x$ on the same plane and then find the intervals where the graph of the left side will lie down the graph of the right side.

We note from the two graphs that the graph of the function
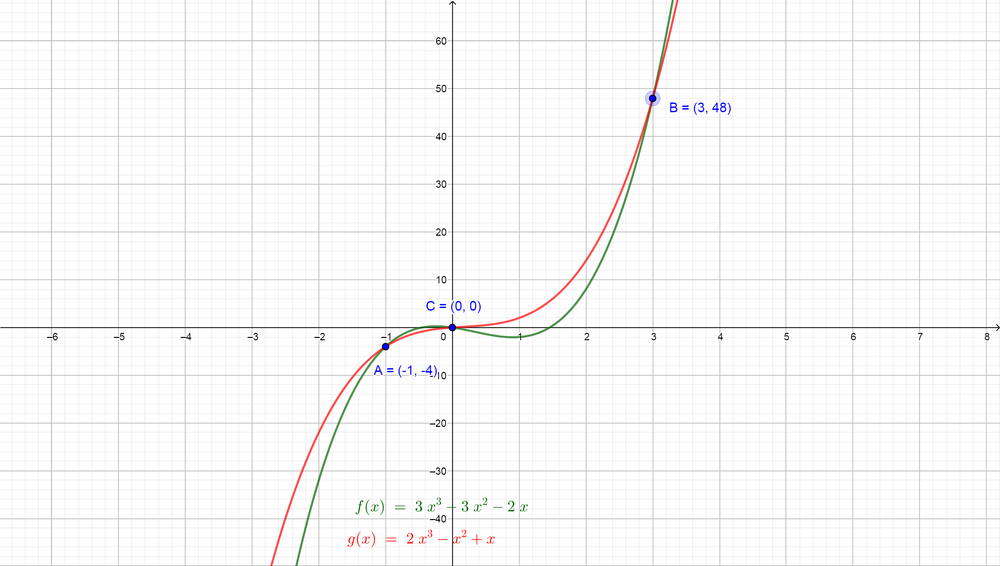
$color{#4257b2}f(x)=3x^{3}-3x^{2}-2x$ lies down or equals the graph of the function
$color{#4257b2}g(x)=2x^{3}-x^{2}+x$ in two cases: the first case for $color{#4257b2}x leq -1$ and the second case for $color{#4257b2}0 leq x leq 3$, so the solutions of our inequality will be at these intervals and this confirm our solution $color{#c34632}x in (-infty, -1] {color{Black}text{or}} x in [0, 3]$.

(f) We would like to solve the inequality $color{#4257b2}x^{3}-x^{2}-3x+3 > -x^{3}+2x+5$. First, we can add $color{#4257b2}x^{3}-2x-5$ to each side to make the right side equals zero.

$$
x^{3}-x^{2}-3x+3+x^{3}-2x-5 > 0
$$

$$
2x^{3}-x^{2}-5x-2 > 0 (1)
$$

Now we have a cubic function in the left side, so we can let
$color{#4257b2}f(x)=2x^{3}-x^{2}-5x-2$ and then we can use the factor theorem and the related polynomial function to determine one factor of the equation where the numbers that could make the function $color{#4257b2}f(x)=0$ are of the form $color{#4257b2}dfrac{p}{q}$where $color{#4257b2}p$ is a factor of the constant term and $color{#4257b2}q$ is a factor of the leading coefficient.

Now we note that our function is $color{#4257b2}f(x)=2x^{3}-x^{2}-5x-2$, so $color{#4257b2}p=2$ and $color{#4257b2}q=2$. As a result the root could be of the form $color{#4257b2}dfrac{2}{2}$ and the factors of it are $color{#4257b2}pm 1, pm 2, pm dfrac{1}{2}$. Now we will calculate the value of the function at each number until we find one of them which makes the function equals zero and then we can can divide the function by this factor.

$$
f(x)=2x^{3}-x^{2}-5x-2
$$

$$
f(1)=2(1)^{3}-(1)^{2}-5(1)-2=-6
$$

$$
f(-1)=2(-1)^{3}-(-1)^{2}-5(-1)-2=0
$$

By the factor theorem, $color{#4257b2}(x+1)$ is a factor of the function $color{#4257b2}f(x)$. Now we can divide the function $color{#4257b2}f(x)$ by the factor term $color{#4257b2}(x+1)$ to find the remaining factors.

$$
polylongdiv{2x^{3}-x^{2}-5x-2}{x+1}
$$

So the function $color{#4257b2}f(x)$ can be rewrite as $color{#4257b2}f(x)=left(x+1right)left(2x^{2}-3x-2right)$. Now the next step is to factor the quadratic function $color{#4257b2}2x^{2}-3x-2$.

$$
f(x)=left(x+1right)left(2x^{2}-3x-2right)
$$

$$
f(x)=left(x+1right)left(x-2right)left(2x+1right)
$$

Now we found the factors of the function $color{#4257b2}f(x)=2x^{3}-x^{2}-5x-2$, so we can substitute in our inequality (1).

$$
left(x+1right)left(x-2right)left(2x+1right) > 0
$$

Now we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
left(x+1right)left(x-2right)left(2x+1right)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$.

$$
x+1=0, x-2=0 text{or} 2x+1=0
$$

$$
x=-1, x=2 text{or} x=-dfrac{1}{2}
$$

Now we find that the roots are $color{#4257b2}-1, -0.5$ and $color{#4257b2}2$, so these numbers will divide the domain to four intervals $color{#4257b2}x<-1, -1<x<-0.5, -0.5<x2$ and the following number line shows these intervals

Now we have three factors of the inequality $color{#4257b2}(x+1), (x-2)$ and $color{#4257b2}(2x+1)$ and we have four intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}(x+1)(x-2)(2x+1)$ will be positive to verify our inequality $color{#4257b2}(x+1)(x-2)(2x+1) > 0$.

We note from the table that the product $color{#4257b2}(x+1)(x-2)(2x+1)$ is positive at the intervals $color{#4257b2}-1 < x 2$, so the solution of the inequality $color{#4257b2}x^{3}-x^{2}-3x+3 > -x^{3}+2x+5$ is $color{#c34632}x in (-1, -0.5) {color{Black}text{or}} x in (2, infty)$.

Now we need to use the graph to confirm our solution for the inequality $color{#4257b2}x^{3}-x^{2}-3x+3 > -x^{3}+2x+5$, so we can graph the function of the left side $color{#4257b2}f(x)=x^{3}-x^{2}-3x+3$ and graph the function of the right side $color{#4257b2}g(x)=-x^{3}+2x+5$ on the same plane and then find the intervals where the graph of the left side will lie above the graph of the right side.

We note from the two graphs that the graph of the function
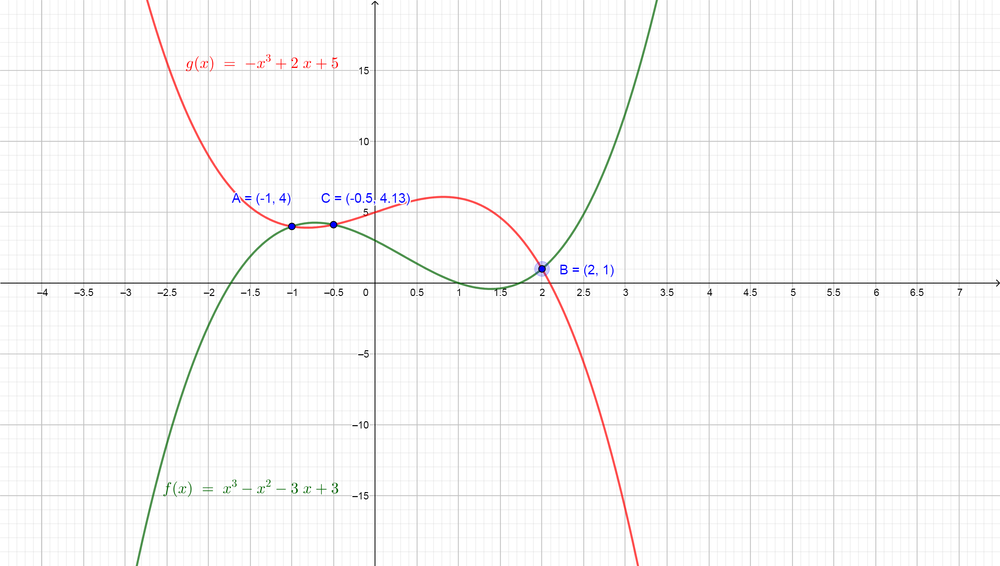
$color{#4257b2}f(x)=x^{3}-x^{2}-3x+3$ lies above the graph $color{#4257b2}g(x)=-x^{3}+2x+5$ in two cases: the first case for $color{#4257b2}-1 < x 2$, so the solutions of our inequality will be at these intervals and this confirm our solution $color{#c34632}x in (-1, -0.5) {color{Black}text{or}} x in (2, infty)$.

Large{$text{color{Brown}(a) $x in (-infty, -1] {color{Black}text{or}} x in [7, infty)$
\
\
(b) $x in (0, 2)$
\
\
(c) $x in (-infty, -3] {color{Black}text{or}} x in [-2, 1]$
\
\
(d) $x in (-infty, -2), x in (-1, 1) {color{Black}text{or}} x in (2, infty)$
\
\
(e) $x in (-infty, -1] {color{Black}text{or}} x in [0, 3]$
\
\
(f) $x in (-1, -0.5) {color{Black}text{or}} x in (2, infty)$}$

We would like to determine when $color{#4257b2}f(x) < g(x)$ in the given graph. First, to know the intervals where $color{#4257b2}f(x) < g(x)$, we need to find the intervals where the graph of $color{#4257b2}f(x)$ lies down the graph of $color{#4257b2}g(x)$.

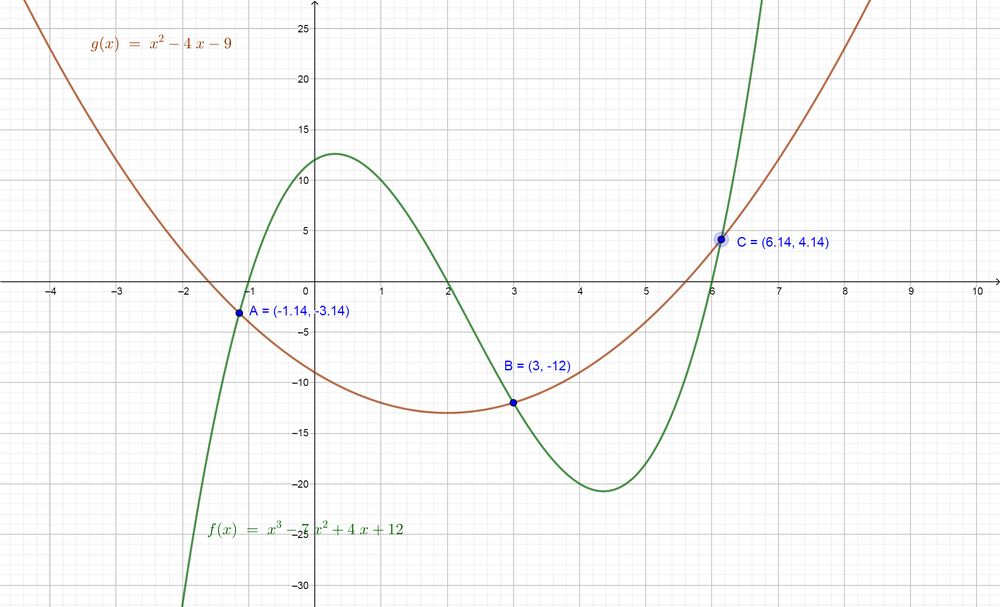
We note from the graph that the function $color{#4257b2}f(x)$ lies down the graph of the function $color{#4257b2}g(x)$ at two intervals $color{#4257b2}-1 < x 2$, so the solution of the inequality $color{#4257b2}f(x) < g(x)$ is $color{#c34632}x in (-1, 1) {color{Black}text{or}} x in (2, infty)$.

Large{$text{color{Brown}$x in (-1, 1) {color{Black}text{or}} x in (2, infty)$}$

(a) We would like to know the equation of the corresponding function for the inequality $color{#4257b2}x^{3}+11x^{2}+18x+10 > 10$. First, we can subtract $color{#4257b2}10$ to make the right side equals zero.

$$
x^{3}+11x^{2}+18x+10 > 10
$$

$$
x^{3}+11x^{2}+18x+10 -10 > 10-10
$$

$$
x^{3}+11x^{2}+18x > 0
$$

Now to find the equation of the corresponding function we can convert the inequality to an equation.

$$
x^{3}+11x^{2}+18x=0
$$

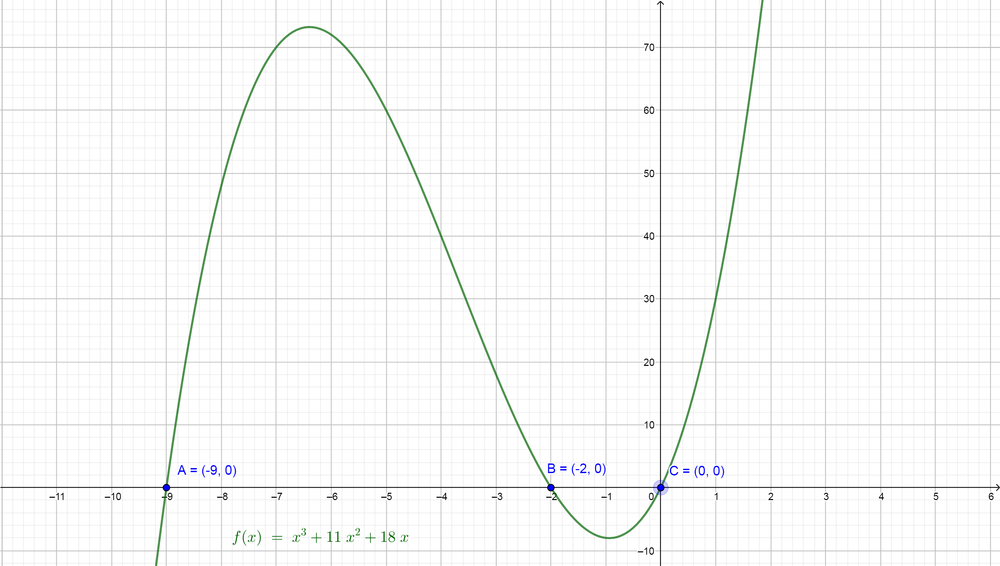
So the equation of the corresponding function is $color{#c34632}x^{3}+11x^{2}+18x=0$.

(b) We would like to explain how the graph of the corresponding function can be used to solve the inequality. First, we find that the corresponding function is $color{#4257b2}x^{3}+11x^{2}+18x$ and our inequality is $color{#4257b2}x^{3}+11x^{2}+18x > 0$, so we can graph the function $color{#4257b2}x^{3}+11x^{2}+18x$ and then find the intervals where this function lie above the x-axis because the right side of the inequality is zero.

We note from the graph of the corresponding function $color{#4257b2}f(x)=x^{3}+11x^{2}+18x$ that it lies above the x-axis in the intervals $color{#4257b2} -9 < x 0$, so the solutions of the inequality $color{#4257b2}x^{3}+11 x^{2}+18 x +10 > 10$ will be at these intervals $color{#c34632}x in (-9, -2) {color{Black}text{or}} x in (0, infty)$.

(c) We would like to solve the inequality $color{#4257b2}x^{3}+11 x^{2}+18 x +10 > 10$ algebraically. First, we can subtract $color{#4257b2}10$ from each side to make the right side equals zero.

$$
x^{3}+11 x^{2}+18 x +10 -10 > 10-10
$$

$$
x^{3}+11 x^{2}+18 x > 0
$$

Now we note that all terms of the left side contain $color{#4257b2}x$, so we can take it as a common factor.

$$
x(x^{2}+11 x+18) > 0
$$

Now the next step is to factor the quadratic function $color{#4257b2}x^{2}+11 x+18$.

$$
xleft(x+2right)left(x+9right) > 0
$$

Now we can convert this inequality to an equation to determine the roots of the corresponding polynomial equation.

$$
xleft(x+2right)left(x+9right)=0
$$

$$
x=0, x+2=0 text{or} x+9=0
$$

$$
x=0, x=-2 text{or} x=-9
$$

Now we find that the roots are $color{#4257b2}-9, -2$ and $color{#4257b2}0$, so these numbers will divide the domain to four intervals $color{#4257b2}x<-9, -9<x<-2, -2<x0$ and the following number line shows these intervals

Now we have three factors of the inequality $color{#4257b2}x, (x+2)$ and $color{#4257b2}(x+9)$ and we have four intervals, so the next step is to create a table to consider the sign of each factor at each interval and then determine the sign of their products to know the intervals where $color{#4257b2}x(x+2)(x+9)$ will be negative or equals zero to verify our inequality $color{#4257b2}x(x+2)(x+9) > 0$.

We note from the table that the product $color{#4257b2}x(x+2)(x+9)$ is positive at the intervals $color{#4257b2}-9 < x 0$, so the solution of the inequality $color{#4257b2}x^{3}+11 x^{2}+18 x +10 > 10$ is $color{#c34632}x in (-9, -2) {color{Black}text{or}} x in (0, infty)$.

Large{$text{color{Brown}$x in (-9, -2) {color{Black}text{or}} x in (0, infty)$}$

We would like to write an expression for $color{#4257b2}f(x)$ in which $color{#4257b2}f(x)$ is a quartic function, $color{#4257b2}f(x)>0$ when $color{#c34632}-2 < x< 1$, $color{#4257b2}f(x) leq 0$ when $color{#c34632}x 1$, $color{#4257b2}f(x)$ has two roots at $color{#c34632}x=3$, and $color{#4257b2}f(-1)=96$.

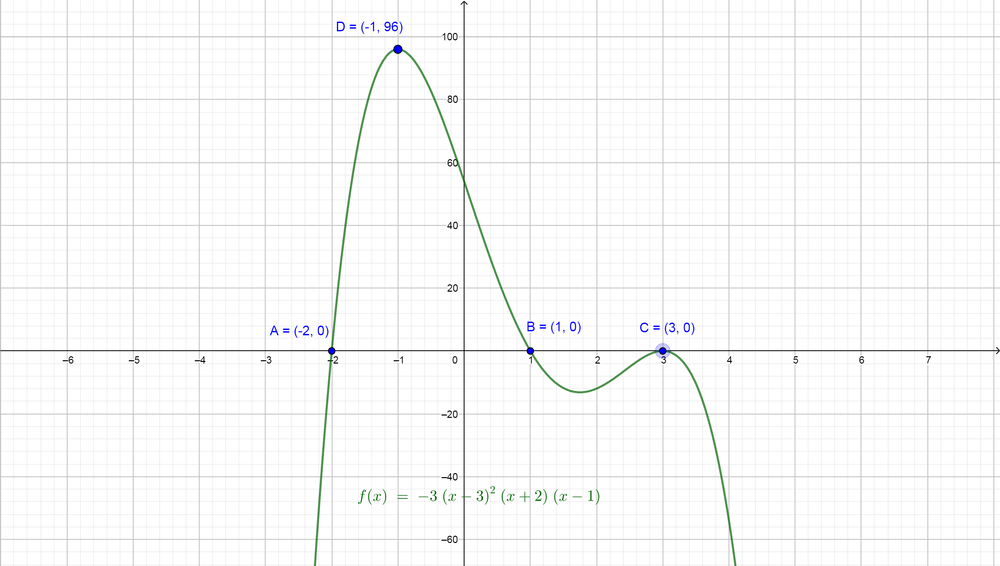
First, we know that our function is quartic, so we can write it in the form of factors $color{#4257b2}f(x)=a(x+b)(x+c)(x+d)(x+e)$ where these factors is the factors which will make the equation equals zero and our target now is to find the value of each factor. Now we will use the given information to find these values.

We note from the given information that the values of $color{#4257b2}x=-2 {color{Black}text{and}} x=1$ divide the domain of the function to three intervals
$color{#4257b2}x < -2, -2 < x 2$, so the numbers $color{#4257b2}-2 {color{Black}text{and}} 1$ are two roots of the function $color{#4257b2}f(x)$ which means that the factors $color{#4257b2}(x+2) {color{Black}text{and}} (x-1)$ are two factors which makes the function $color{#4257b2}f(x)$ zero.

Also we note from the given information that $color{#4257b2}f(x)$ has two roots at $color{#4257b2}x=3$, so we can write the factors of these two roots as $color{#4257b2}(x-3)^{2}$ where the factor in this from means that there are two similar roots each of them equals $color{#4257b2}3$.

Now we found the four factors of the function, so we can write our function as $color{#4257b2}f(x)=a (x-3)^{2}(x+2)(x-1)$. Now the final step is to find the value of the constant $color{#4257b2}a$ and we can use the information $color{#4257b2}f(-1)=96$ to find it as follows:

$$
f(x)=a (x-3)^{2}(x+2)(x-1)
$$

$$
f(-1)=a (-1-3)^{2}(-1+2)(-1-1)=96
$$

$$
a (-4)^{2}(1)(-2)=96
$$

$$
a (16)(2)(-2)=96
$$

$$
-32 a=96
$$

Now we can divide the two sides by $color{#4257b2}-32$ to find the value of $color{#4257b2}a$.

$$
dfrac{-32 a}{-32}=dfrac{96}{-32}
$$

$$
a=-3
$$

Now we have the value of the constant $color{#4257b2}a$, so the function will be
$$
color{#c34632}f(x)=-3(x-3)^{2}(x+2)(x-1)
$$

Now we can use the graph calculator to graph the function $color{#4257b2}f(x)=-3(x-3)^{2}(x+2)(x-1)$ to check that our solution is true and verifies all the given information.

We note from the graph of the function $color{#4257b2}f(x)$ that it verifies all the given information where it is positive at the interval $color{#4257b2}-2 < x < 1$ and it is negative or equals zero at the intervals $color{#4257b2}x1$ and there are two roots at $color{#4257b2}x=3$ and the value of the function at $color{#4257b2}x=-1$ is $color{#4257b2}96$, so the solution of $color{#c34632}f(x)=-3(x-3)^{2}(x+2)(x-1)$ is true.

Large{$text{color{Brown}$f(x)=-3(x-3)^{2}(x+2)(x-1)$}$

Rock is tossed from a platform and through a parabolic pass through the air. The high of the rock in the air is represented by, $h(t)=-5t^2+12t+14$, and time $(t)$ measured in second. Answer for the following questions.

$$
text{color{#4257b2}(a) How high is the rock off the ground when its thrown?}
$$

At second of the rock is thrown, the time is equal zero as follows:

$$
h(t)=-5(0)^2+12(0)+14 h(t)=0+0+14
$$

The high of the rock off the ground at moment of thrown is equal $(14)$ meter.

$$
text{color{#4257b2}(b) How long is the rock in the air?}
$$

In the air the rook high is equal zero as follows:

$$
0=-5t^2+12t+14
$$

Use discriminant property for quadratic equation $left[t=dfrac{-bpmsqrt{b^2-4ac}}{2a}right]$ as follows:

$$
a=-5 b=12 c=14
$$

$$
t=dfrac{-12pmsqrt{(12)^2-(4cdot-5cdot14)}}{2cdot-5} t=dfrac{-12pmsqrt{144+280}}{-10}
$$

$$
t=dfrac{-12+sqrt{424}}{-10} t=-0.859 text{second}
$$

$$
t=dfrac{-12-sqrt{424}}{-10} t=3.259 text{second}
$$

The rock will be in the air for $(3.259)$ second.

$$
text{color{#4257b2}(c) For what time the height of the rock is greater than $(17)$ meter?}
$$

$$
-5t^2+12t+14>17 -5t^2+12t>17-14 -5t^2+12t>3
$$

Use greatest common factor as follows:

$$
-t(5t+12)>3
$$

Use zero property as follows:

$$
-t>3 t3 5t>3-12 5t>-9
$$

Divide entire inequality by $(5)$ as follows:

$$
t>-dfrac{9}{5} t>-1.8
$$

The negative value is not reality, so the correct time is $(t<3)$.

The height of the rock is greater than $(17)$ meter at, $(t<3)$ second.

$$
text{color{#4257b2}(d) How long is the rock above $(17)$ meter?}
$$

Time of the rock above $(17)$ meter is equal $(1.8)$ second

$$
text{color{Brown}(a) The high of the rock off the ground at moment of thrown is equal $(14)$ meter.
\ \
(b) $t=3.259 text{second}$.
\ \
(c) The height of the rock is greater than $(17)$ meter at, $(t<3)$ second.
\ \
(d) Time of the rock above $(17)$ meter is equal $(1.8)$ second.}
$$

An open topped box can be formed square corner cut from a $(30)$ cm by $(20)$ cm cardboard to create a box. Volume of new box represented by, $V(x)=x(30-2x)(20-2x)$, where $(x)$ is the height, answer for the following question.

$$
text{color{#4257b2}(a) Calculate the volume of the box with height of $(2)$ cm}
$$

$$
V(x)=x(30-2x)(20-2x)
$$

Substitute the value of $(x=2)$ as follows:

$$
V(x)=2cdot [30-2(2)]cdot [20-2(2)] V(x)=2 cdot (26) cdot (16)
$$

$$
V(x)=832 text{cm}^3
$$

$$
text{color{#4257b2}(b) Calculate the dimensions of the box with a volume of $(1000)$ cm$^3$}
$$

$$
V(x)=x(30-2x)(20-2x)
$$

Use distributive property as follows:

$$
1000=x left[600-60x-40x+4x^2right] V(x)=4x^3-100x^2+600x=1000
$$

$$
{V}'(x)=12x^2-200x+600=0
$$

Divide the entire equation by $(4)$ as follows:

$$
3x^2-50x+150=0
$$

Use discriminant property for quadratic equation $left[x=dfrac{-bpmsqrt{b^2-4ac}}{2a}right]$ as follows:

$$
a=3 b=-50 c=150
$$

$$
x=dfrac{50pmsqrt{(50)^2-(4cdot3cdot150)}}{2cdot3} x=dfrac{50pmsqrt{2500-1800}}{6}
$$

$$
x=dfrac{50+sqrt{700}}{6} x=12.74
$$

$$
x=dfrac{50-sqrt{700}}{6} x=3.92
$$

$$
V(x)=x(30-2x)(20-2x)
$$

Use zero property to find the range value of $(x)$ as follows:

$$
30-2xge0 -2xge-30 xle15
$$

$$
20-2xge0 -2xge-20 xle10
$$

According these ranges values of $(x)$, the matched value of $(x)$ is equal, $(3.92)$

The dimensions of box are:

Height $=3.92$ cm

Length $=30-2(3.92)=22.16$ cm

Width $=20-2(3.92)=12.16$ cm

$$
text{color{Brown}(a) $V(x)=832 text{cm}^3$
\ \
(b) Height $=6.068$ cm Length $=37.864$ cm Width $=17.864$ cm}
$$

*(b)* if we subtract $30+11x^2$ throughout, we obtain
$$
-4x^{12}-7x^6-2x^2-10<0.$$

Note that all exponents on the left-hand side of inequality are even. An even degree of any real number is always a positive number. Since on the left-hand side we only have a subtraction of positive numbers, the result is less than zero for any value of $x$. Hence, $-infty< x< infty$.

$$
text{color{#4257b2}Correct and solve the mistake in the textbook for solving the inequality}
$$

$$
(x+1)(x-2)>(x+1)(-x+6)
$$

Use distributive property as follows:

$$
x^2-x-2>x^2+5x+6
$$

Add entire inequality by $(-x^2+x)$ as follows:

$$
-2>6x+6
$$

Add entire inequality by $(-6)$ as follows:

$$
-8>6x
$$

Divide the inequality by $(6)$ as follows:

$$
-dfrac{4}{3}>x
$$

$therefore$ The solution set is $left(-infty, -dfrac{4}{3} right)$

$$
text{color{Brown} $left(-infty, -dfrac{4}{3} right)$}
$$

Solve the following inequalities.

$$
color{#4257b2}text{(a)} dfrac{x^2+x-12}{x^2+5x+6}<0
$$

Multiply entire inequality by $left(x^2+5x+6right)$ as follows:

$$
x^2+x-12<0 (x+4)(x-3)<0
$$

$$
x=-4 x=3
$$

Intervals are: $x<-4, -4<x3$

Determine the value of polynomial according each interval as follows:

For $x<-4 f(-5)=8$ For $-4<x3 f(4)=8$

According the inequality $f(x)<0$, the true interval which make the inequalities true are:

$$
-4<x<3
$$

$$
color{#4257b2}text{(b)} dfrac{x^2-25}{x^3+6x^2+5x}>0
$$

Multiply entire inequality by $left(x^3+6x^2+5xright)$ as follows:

$$
x^2-25>0 (x-5)(x+5)>0
$$

$$
x=5 x=-5
$$

Intervals are: $x<-5, -5<x5$

Determine the value of polynomial according each interval as follows:

For $x<-5 f(-6)=11$ For $-5<x5 f(6)=11$

According the inequality $f(x)>0$, the true interval which make the inequalities true are:

$$
x5
$$

$$
text{color{Brown}(a) $-4<x<3$
\ \
(b) $x5$}
$$

When we have factored the form of a polynomial, it is convenient to solve the inequality using the table of values. Note that

$$x+1=0implies x=-1$$
and
$$x-2=0implies x=2$$

and that $2^x$ is always positive, for any value of $x$. These two solutions for $x$ break the real line into three intervals: $x<-1$, $-1< x2$. For each of these intervals, we can check the sign of every factor and put in the table. Afterward multiplying the obtained signs we can compute the sign of the whole polynomial. Note that the product of same signs is always positive, while the product of opposite signs is always negative.

We build *Table 1* in which we check the sign of every factor for every interval:
$$
begin{array}{ |c | c | c |c|}
hline
&x<-1 &-1<x2 \
hline
x+1& -&+ &+ \
hline
x-2& -&- &+ \
hline
2^x& +&+ &+ \
hlinehline
text{product}&+&-&+\
hline
end{array}
$$

*Table 1.* The sign of each factor

Note that we seek for the solutions for which the expression is greater than zero. From the table we can read out the intervals for which the product row has a plus sign. Hence, that yields

$$x2$$

$$xin (-infty,-1]cup[2,infty).$$

$xin (-infty,-1]cup[2,infty)$