Divide $x^4-16x^3+4x^2+10x-11$ by the following binomials.

$$
color{#4257b2}text{(I)} (x-2)
$$

Use $(x=2)$ to divide the equation as follows:

$$
begin{align*}
2| &=1 -16 4 10 -11
\ \
&= 2 -28 -48 -76
\ \
&=1 -14 -24 -38 -87
end{align*}
$$

$$
x^4-16x^3+4x^2+10x-11=(x-2)(x^3-14x^2-24x-38)-87
$$

$$
color{#4257b2}text{(II)} (x+4)
$$

Use $(x=-4)$ to divide the equation as follows:

$$
begin{align*}
-4| &=1 -16 4 10 -11
\ \
&= -4 80 -336 1304
\ \
&=1 -20 84 -326 1293
end{align*}
$$

$$
x^4-16x^3+4x^2+10x-11=(x+4)(x^3-20x^2+84x-326)+1293
$$

$$
color{#4257b2}text{(III)} (x-1)
$$

Use $(x=1)$ to divide the equation as follows:

$$
begin{align*}
1| &=1 -16 4 10 -11
\ \
&= 1 -15 -11 -1
\ \
&=1 -15 -11 -1 -12
end{align*}
$$

$$
x^4-16x^3+4x^2+10x-11=(x-1)(x^3-15x^2-11x-1)-12
$$

(b) There are no factors for givens binomials.

$$
text{color{Brown} (a) (I) $(x-2)(x^3-14x^2-24x-38)-87$
\ \
(II) $(x+4)(x^3-20x^2+84x-326)+1293$
\ \
(III) $(x-1)(x^3-15x^2-11x-1)-12$
\ \
(b) There are no factors for givens binomials.}
$$

State the degree of the quotient for the following expression.

$$
color{#4257b2}text{(a)} x^4-15x^3+2x^2+12x-10 div x^2-4
$$

Divide the first term for both expressions as follows:

$$
dfrac{x^4}{x^2}=x^2
$$

The degree of quotient is $n=2$

$$
color{#4257b2}text{(b)} 5x^3-4x^2+3x-4 div x+3
$$

Divide the first term for both expressions as follows:

$$
dfrac{5x^3}{x}=5x^2
$$

The degree of quotient is $n=2$

$$
color{#4257b2}text{(c)} x^4-7x^3+2x^2+9x div x^3-x^2+2x+1
$$

Divide the first term for both expressions as follows:

$$
dfrac{x^4}{x^3}=x
$$

The degree of quotient is $n=1$

$$
color{#4257b2}text{(d)} 2x^2+5x-4 div x^4+3x^3-5x^2+4x-2
$$

Divide the first term for both expressions as follows:

$$
dfrac{2x^2}{x^4}=dfrac{2}{x^2}
$$

The degree of quotient is $n=-2$

$$
text{color{Brown}(a)$n=2$ (b) $n=2$ (c) $n=1$ (d) $n=-2$}
$$

(a) Divided function $(x^4-15x^3+2x^2+12x-10)$ by $(x^2-4)$

Divided the first term for tow expressions as follows:

$$
=dfrac{x^4}{x^2}=x^2
$$

Then multiply it $(x^2)$with $(x^2-4)$ as follows:

$$
=x^4-4x^2 text{reverse}=-x^4+4x^2
$$

Subtract the reverse result with $(x^4-15x^3+2x^2+12x-10)$ as follows:

$$
cancel x^4-15x^3+2x^2+12x-10cancel-x^4+4x^2 -15x^3+6x^2+12x-10
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-15x^3}{x^2}=-15x
$$

Then multiply it $(-15x)$with $(x^2-4)$ as follows:

$$
=-15x^2+60x text{reverse}=15x^2-60x
$$

Subtract the reverse result with $(-15x^3+6x^2+12x-10)$ as follows:

$$
cancel-15x^3+6x^2+12x-10cancel+15x^2-60x=0 6x^2-48x-10
$$

Divided the first term for the two question s as follows:

$$
=dfrac{6x^2}{x^2}=6
$$

Then multiply it $(6)$with $(x^2-4)$ as follows:

$$
=6x^2-24 text{reverse}=-6x^2+24
$$

Subtract the reverse result with $(6x^2-48x-10)$ as follows:

$$
cancel6x^2-48x-10cancel-6x^2+24=0 -48x+14
$$

$$
(x^4-15x^3+2x^2+12x-10)=(x^2-4)(x^2-15x+6)-48x+14
$$

(b) Divided function $(5x^3-4x^2+3x-4)$ by $(x+3)$

Divided the first term for tow expressions as follows:

$$
=dfrac{5x^3}{x}=5x^2
$$

Then multiply it $(5x^2)$with $(x+3)$ as follows:

$$
=5x^3+15x^2 text{reverse}=-5x^3-15x^2
$$

Subtract the reverse result with $(5x^3-4x^2+3x-4)$ as follows:

$$
cancel 5x^3-4x^2+3x-4cancel-5x^3-15x^2 =-19x^2+3x-4
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-19x^2}{x}=-19x
$$

Then multiply it $(-19x)$with $(x+3)$ as follows:

$$
=-19x^2-57x text{reverse}=19x^2+57x
$$

Subtract the reverse result with $(-19x^2+3x-4)$ as follows:

$$
cancel-19x^2+3x-4cancel+19x^2+57x=0 =60x-4
$$

Divided the first term for the two question s as follows:

$$
=dfrac{60x}{x}=60
$$

Then multiply it $(60)$with $(x+3)$ as follows:

$$
=6x+180 text{reverse}=-6x-180
$$

Subtract the reverse result with $(6x^2-48x-10)$ as follows:

$$
cancel6x-4cancel-6-180=0 =-184
$$

$$
(5x^3-4x^2+3x-4)=(x+3)(5x^2-19x+60)-184
$$

(c) Divided function $(x^4-7x^3+2x^2+9x)$ by $(x^3-x^2+2x+1)$

Divided the first term for tow expressions as follows:

$$
=dfrac{x^4}{x^3}=x
$$

Then multiply it $(x)$with $(x^3-x^2+2x+1)$ as follows:

$$
=x^4-x^3+2x^2+x text{reverse}=-x^4+x^3-2x^2-x
$$

Subtract the reverse result with $(x^4-7x^3+2x^2+9x)$ as follows:

$$
cancel x^4-7x^3+2x^2+9xcancel-x^4+x^3-2x^2-x -6x^3+8x
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-6x^3}{x^3}=-6
$$

Then multiply it $(-6)$with $(x^3-x^2+2x+1)$ as follows:

$$
=-6x^3+6x^2-12x-6 text{reverse}=6x^3-6x^2+12x+6
$$

Subtract the reverse result with $(-6x^3+8x)$ as follows:

$$
cancel-6x^3+8xcancel+6x^3-6x^2+12x+6=0 =-6x^2+20x+6
$$

$$
(x^4-7x^3+2x^2+9x)=(x-6)(x^3-x^2+2x+1)-6x^2+20x+6
$$

(d) Divided function $(2x^2+5x-4)$ by $(x^4+3x^3-5x^2+4x-2)$

Divided the first term for tow expressions as follows:

$$
=dfrac{2x^2}{x^4}=dfrac{2}{x^2}
$$

This operation is not valid, because the degree of lower is greater than the degree of upper.

$$
text{color{Brown}(a) $(x^2-4)(x^2-15x+6)-48x+14$
\ \
(b) $(x+3)(5x^2-19x+60)-184$
\ \
(c) $(x-6)(x^3-x^2+2x+1)-6x^2+20x+6$
\ \
(d) Not valid operation.}
$$

Complete the table in the textbook.

$$
text{color{#4257b2}First row.}
$$

$$
text{Reminder}=2x^3-5x^2+8x+4-[(x+3)(2x^2-11x+41)]
$$

$$
text{Reminder}=2x^3-5x^2+8x+4-[2x^3-11x^2+41x+6x^2-33x+123]
$$

$$
=2x^3-5x^2+8x+4-2x^3+11x^2-41x-6x^2+33x-123
$$

Rearrange the tiles to group like terms as follows:

$$
=(2x^3-2x^3)+(-5x^2+11x^2-6x^2)+(8x-41x+33x)+123
$$

$$
text{Reminder}=123
$$

$$
text{color{#4257b2}Second row.}
$$

$$
text{Dividend}=(2x+4)(3x^3-5x+8)-3
$$

Use distributive propery as follows:

$$
=6x^4-10x^2+16x+24x^3-20x+32-3
$$

Rearrange the tiles to group like terms as follows:

$$
=6x^4+24x^3-10x^2-4x+29
$$

$$
text{Dividend}=6x^4+24x^3-10x^2-4x+29
$$

$$
text{color{#4257b2}Third row.}
$$

$$
text{Divisor}=6x^4+2x^3+3x^2-11x-9+5 div 2x^3+x-4
$$

$$
=6x^4+2x^3+3x^2-11x-4 div 2x^3+x-4
$$

Divided the first term for the two question s as follows:

$$
=dfrac{6x^4}{2x^3}=3x
$$

Then multiply it $(3x)$with $(2x^3+x-4)$ as follows:

$$
=6x^4+3x^2-12x text{reverse}=-6x^4-3x^2+12x
$$

Subtract the reverse result with $(6x^4+2x^3+3x^2-11x-4)$ as follows:

$$
cancel 6x^4+2x^3+3x^2-11x-4cancel-6x^4-3x^2+12x
$$

$$
2x^3+x-4
$$

Divided the first term for the two question s as follows:

$$
=dfrac{2x^3}{2x^3}=1
$$

Then multiply it $(1)$with $(2x^3+x-4)$ as follows:

$$
=2x^3+x-4 text{reverse}=-2x^3-x+4
$$

Subtract the reverse result with $(2x^3+x-4)$ as follows:

$$
cancel2x^3+x-4cancel-2x^3-x+4=0
$$

Divisor $=3x+1$

$$
text{color{#4257b2}Forth row.}
$$

$$
text{Quotient}=3x^3+x^2-6x+16-8 div x+2
$$

$$
=6x^4+2x^3+3x^2-11x+8 div x+2
$$

Divided the first term for the two question s as follows:

$$
=dfrac{6x^4}{x}=6x^3
$$

Then multiply it $(6x^3)$with $(x+2)$ as follows:

$$
=6x^4+12x^3 text{reverse}=-6x^4-12x^3
$$

Subtract the reverse result with $(6x^4+2x^3+3x^2-11x+8)$ as follows:

$$
cancel 6x^4+2x^3+3x^2-11x+8cancel-6x^4-12x^3
$$

$$
-10x^3+3x^2-11x+8
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-10x^3}{x}=-10x^2
$$

Then multiply it $(-10x^2)$with $(x+2)$ as follows:

$$
=-10x^3-20x^2 text{reverse}=10x^3+20x^2
$$

Subtract the reverse result with $(-10x^3+3x^2-11x+8)$ as follows:

$$
cancel-10x^3+3x^2-11x+8+cancel10x^3+20x^2=0 23x^2-11x+8
$$

Divided the first term for the two question s as follows:

$$
=dfrac{23x^2}{x}=23x
$$

Then multiply it $(23x)$with $(x+2)$ as follows:

$$
=23x^2+46x text{reverse}=-23x^2-46x
$$

Subtract the reverse result with $(23x^2-11x+8)$ as follows:

$$
cancel23x^2-11x+8cancel-23x^2-46x=0 -57x+8
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-57x}{x}=-57
$$

Then multiply it $(-57)$with $(x+2)$ as follows:

$$
=-57x-114 text{reverse}=57x+114
$$

Subtract the reverse result with $(-57x+8)$ as follows:

$$
cancel-57x+8+cancel57x+114=0 122
$$

$$
text{Quotient}=6x^3-10x^2+23x-57
$$

$$
text{color{Brown}$text{Reminder}=123$
\ \
$text{Dividend}=6x^4+24x^3-10x^2-4x+29$
\ \
Divisor $=3x+1$
\ \
$text{Quotient}=6x^3-10x^2+23x-57$}
$$

$$
text{color{#4257b2}(a) Divided function $(x^3-2x+1)$ by $(x-4)$}
$$

$$
=dfrac{x^3}{x}=x^2
$$

Then multiply it $(x^2)$with $(x-4)$ as follows:

$$
=x^3-4x^2 text{reverse}=-x^3+4x^2
$$

Subtract the reverse result with $(x^3-2x+1)$ as follows:

$$
cancel x^3-2x+1cancel-x^3+4x^2 4x^2-2x+1
$$

Divided the first term for the two question s as follows:

$$
=dfrac{4x^2}{x}=4x
$$

Then multiply it $(4x)$with $(x-4)$ as follows:

$$
=4x^2-16x text{reverse}=-4x^2+16x
$$

Subtract the reverse result with $(4x^2-2x+1)$ as follows:

$$
cancel4x^2-2x+1cancel-4x^2+16x=0
$$

$$
14x+1
$$

Divided the first term for the two question s as follows:

$$
=dfrac{14x}{x}=14
$$

Then multiply it $(14)$with $(x-4)$ as follows:

$$
=14x-56 text{reverse}=-14x+56
$$

Subtract the reverse result with $(14x+1)$ as follows:

$$
cancel14x+1cancel-14x+56=0 =57
$$

$$
(x^3-2x+1)=(x-4)(x^2+4x+14)+57
$$

$$
text{color{#4257b2}(b) Divided function $(x^3+2x^2-6x+1)$ by $(x+2)$}
$$

$$
=dfrac{x^3}{x}=x^2
$$

Then multiply it $(x^2)$with $(x+2)$ as follows:

$$
=x^3+2x^2 text{reverse}=-x^3-2x^2
$$

Subtract the reverse result with $(x^3+2x^2-6x+1)$ as follows:

$$
cancel x^3+2x^2-6x+1cancel-x^3-2x^2 -6x+1
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-6x}{x}=-6
$$

Then multiply it $(-6)$with $(x+2)$ as follows:

$$
=-6x-12 text{reverse}=6x+12
$$

Subtract the reverse result with $(-6x+1)$ as follows:

$$
cancel-6x+1cancel+6x+12=0 =13
$$

$$
(x^3+2x^2-6x+1)=(x+2)(x^2-6)+13
$$

$$
text{color{#4257b2}(c) Divided function $(2x^3+5x^2-4x-5)$ by $(2x+1)$}
$$

$$
=dfrac{2x^3}{2x}=x^2
$$

Then multiply it $(x^2)$with $(2x+1)$ as follows:

$$
=2x^3+x^2 text{reverse}=-2x^3-x^2
$$

Subtract the reverse result with $(2x^3+5x^2-4x-5)$ as follows:

$$
cancel 2x^3+5x^2-4x-5cancel-2x^3-x^2 4x^2-4x-5
$$

Divided the first term for the two question s as follows:

$$
=dfrac{4x^2}{2x}=2x
$$

Then multiply it $(2x)$with $(2x+1)$ as follows:

$$
=4x^2+2x text{reverse}=-4x^2-2x
$$

Subtract the reverse result with $(4x^2-4x-5)$ as follows:

$$
cancel4x^2-4x-5cancel-4x^2-2x=0
$$

$$
-6x-5
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-6x}{2x}=-3
$$

Then multiply it $(-3)$with $(2x+1)$ as follows:

$$
=-6x-3 text{reverse}=6x+3
$$

Subtract the reverse result with $(-6x-5)$ as follows:

$$
cancel-6x-5cancel+6x+3=0 =-2
$$

$$
(2x^3+5x^2-4x-5)=(2x+1)(x^2+2x-3)-2
$$

$$
text{color{#4257b2}(d) Divided function $(x^4+3x^3-2x^2+5x-1)$ by $(x^2+7)$}
$$

$$
=dfrac{x^4}{x^2}=x^2
$$

Then multiply it $(x^2)$with $(x^2+7)$ as follows:

$$
=x^4+7x^2 text{reverse}=-x^4-7x^2
$$

Subtract the reverse result with $(x^4+3x^3-2x^2+5x-1)$ as follows:

$$
cancel x^4+3x^3-2x^2+5x-1cancel-x^4-7x^2 3x^3-9x^2+5x-1
$$

Divided the first term for the two question s as follows:

$$
=dfrac{3x^3}{x^2}=3x
$$

Then multiply it $(3x)$with $(x^2+7)$ as follows:

$$
=3x^3+21x text{reverse}=-3x^3-21x
$$

Subtract the reverse result with $(3x^3-9x^2+5x-1)$ as follows:

$$
cancel3x^3-9x^2+5x-1cancel-3x^3-21x=0
$$

$$
-9x^2-16x-1
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-9x^2}{x^2}=-9
$$

Then multiply it $(-9)$with $(x^2+7)$ as follows:

$$
=-9x^2-63 text{reverse}=9x^2+63
$$

Subtract the reverse result with $(-9x^2-16x-1)$ as follows:

$$
cancel-9x^2-16x-1cancel+9x^2+63=0 =-16x+62
$$

$$
(x^4+3x^3-2x^2+5x-1)=(x^2+7)(x^2+3x-9)-16x+62
$$

$$
text{color{#4257b2}(e) Divided function $(x^4+6x^2-8x+12)$ by $(x^3-x^2-x+1)$}
$$

$$
=dfrac{x^4}{x^3}=x
$$

Then multiply it $(x)$with $(x^3-x^2-x+1)$ as follows:

$$
=x^4-x^3-x^2+x text{reverse}=-x^4+x^3+x^2-x
$$

Subtract the reverse result with $(x^4+6x^2-8x+12)$ as follows:

$$
cancel x^4+6x^2-8x+12cancel-x^4+x^3+x^2-x x^3+7x^2-9x+12
$$

Divided the first term for the two question s as follows:

$$
=dfrac{x^3}{x^3}=1
$$

Then multiply it $(1)$with $(x^3-x^2-x+1)$ as follows:

$$
=x^3-x^2-x+1 text{reverse}=-x^3+x^2+x-1
$$

Subtract the reverse result with $(x^3+7x^2-9x+12)$ as follows:

$$
cancel x^3+7x^2-9x+12cancel-x^3+x^2+x-1=0
$$

$$
8x^2-8x+11
$$

$$
(x^4+6x^2-8x+12)=(x^3-x^2-x+1)(x+1)+8x^2-8x+11
$$

$$
text{color{#4257b2}(f) Divided function $(x^5+4x^4+9x+8)$ by $(x^4+x^3+x^2+x-2)$}
$$

$$
=dfrac{x^5}{x^4}=x
$$

Then multiply it $(x)$with $(x^4+x^3+x^2+x-2)$ as follows:

$$
=x^5+x^4+x^3+x^2-2x text{reverse}=-x^5-x^4-x^3-x^2+2x
$$

Subtract the reverse result with $(x^5+4x^4+9x+8)$ as follows:

$$
cancel x^5+4x^4+9x+8cancel-x^5-x^4-x^3-x^2+2x 3x^4-x^3-x^2+11x+8
$$

Divided the first term for the two question s as follows:

$$
=dfrac{3x^4}{x^4}=3
$$

Then multiply it $(3)$with $(x^4+x^3+x^2+x-2)$ as follows:

$$
=3x^4+3x^3+3x^2+3x-6 text{reverse}=-3x^4-3x^3-3x^2-3x+6
$$

Subtract the reverse result with $(3x^4-x^3-x^2+11x+8)$ as follows:

$$
cancel 3x^4-x^3-x^2+11x+8cancel-3x^4-3x^3-3x^2-3x+6=0
$$

$$
-4x^3-4x^2+8x+14
$$

$$
(x^5+4x^4+9x+8)=(x^4+x^3+x^2+x-2)(x+3)-4x^3-4x^2+8x+14
$$

$$
text{color{Brown}(a) $(x-4)(x^2+4x+14)+57$
\ \
(b) $(x+2)(x^2-6)+13$
\ \
(c) $(2x+1)(x^2+2x-3)-2$
\ \
(d) $(x^2+7)(x^2+3x-9)-16x+62$
\ \
(e) $(x^3-x^2-x+1)(x+1)+8x^2-8x+11$
\ \
(f) $(x^4+x^3+x^2+x-2)(x+3)-4x^3-4x^2+8x+14$}
$$

Calculate the following expressions

$$
color{#4257b2}text{(a)} x^3-7x-6 text{divisor}=x-3
$$

$(x-3)$ is the factor, so use $(x=3)$ to divide the equation as follows:

$$
begin{align*}
3| &=1 0 -7 -6
\ \
&= 3 9 6
\ \
&=1 3 2 0
end{align*}
$$

$$
x^3-7x-6=(x-3)(x^2+3x+2)
$$

$$
x^3-7x-6=(x-3)(x+2)(x+1)
$$

$$
color{#4257b2}text{(b)} 2x^3-7x^2-7x+19 text{divisor}=x-1
$$

$(x-1)$ is the factor, so use $(x=1)$ to divide the equation as follows:

$$
begin{align*}
1| &=2 -7 -7 19
\ \
&= 2 -5 -12
\ \
&=2 -5 -12 7
end{align*}
$$

$$
2x^3-7x^2-7x+19=(x-1)(2x^2-5x-12)+7
$$

$$
2x^3-7x^2-7x+19=(x-1)(2x+3)(x-4)+7
$$

$$
color{#4257b2}text{(c)} 6x^4+13x^3-34x^2-47x+28 text{divisor}=x+3
$$

$(x+3)$ is the factor, so use $(x=-3)$ to divide the equation as follows:

$$
begin{align*}
-3| &=6 13 -34 -47 28
\ \
&= -18 15 57 -30
\ \
&=6 -5 -19 10 -2
end{align*}
$$

$$
6x^4+13x^3-34x^2-47x+28=(x+3)(6x^3-5x^2-19x+10)-2
$$

$$
color{#4257b2}text{(d)} 2x^3+x^2-22x+20 text{divisor}=2x-3
$$

$(2x-3)$ is the factor, so use $left(x=dfrac{3}{2}right)$ to divide the equation as follows:

$$
begin{align*}
tfrac{3}{2}| &=2 1 -22 20
\ \
&= 3 6 -24
\ \
&=2 4 -16 -4
end{align*}
$$

$$
2x^3+x^2-22x+20=(2x-3)(2x^2+4x-16)-4
$$

$$
color{#4257b2}text{(e)} 12x^4-56x^3+59x^2+9x-18 text{divisor}=2x+1
$$

$(2x+1)$ is the factor, so use $(x=-0.5)$ to divide the equation as follows:

$$
begin{align*}
-0.5| &=12 -56 59 9 -18
\ \
&= -6 31 -45 18
\ \
&=12 -62 90 -36 0
end{align*}
$$

$$
12x^4-56x^3+59x^2+9x-18=(2x+1)(12x^3-62x^2+90x-36)
$$

$$
color{#4257b2}text{(f)} 6x^3-15x^2-2x+5 text{divisor}=2x-5
$$

$(2x-5)$ is the factor, so use $left(x=dfrac{5}{2}right)$ to divide the equation as follows:

$$
begin{align*}
tfrac{5}{2}| &=6 -15 -2 5
\ \
&= 15 0 -5
\ \
&=6 0 -2 0
end{align*}
$$

$$
6x^3-15x^2-2x+5=(2x-5)(6x^2-2)-4
$$

$$
6x^3-15x^2-2x+5=2(2x-5)(3x^2-1)-4
$$

$$
text{color{Brown}(a) $(x-3)(x+2)(x+1)$
\ \
(b) $(x-1)(2x+3)(x-4)+7$
\ \
(c) $(x+3)(6x^3-5x^2-19x+10)-2$
\ \
(d) $(2x-3)(2x^2+4x-16)-4$
\ \
(e) $(2x+1)(12x^3-62x^2+90x-36)$
\ \
(f) $2(2x-5)(3x^2-1)-4$}
$$

Determine the dividend for the following terms.

$$
color{#4257b2}text{(a)} (x+10)(x^2-6x+9)-1
$$

Use distributive property as follows:

$$
x(x^2-6x+9)+10(x^2-6x+9)-1
$$

$$
x^3-6x^2+9x+10x^2-60x+90-1
$$

$$
color{Brown}x^3+4x^2-51x+89
$$

$$
color{#4257b2}text{(b)} (3x-2)(x^3+x-12)+15
$$

Use distributive property as follows:

$$
3x(x^3+x-12)-2(x^3+x-12)+15
$$

$$
3x^4+3x^2-36x-2x^3-2x+24+15
$$

$$
color{Brown}3x^4-2x^3+3x^2-38x+39
$$

$$
color{#4257b2}text{(c)} (5x+2)(x^3+4x^2-5x+6)+x-2
$$

Use distributive property as follows:

$$
5x(x^3+4x^2-5x+6)+2(x^3+4x^2-5x+6)+x-2
$$

$$
5x^4+20x^3-25x^2+30x+2x^3+8x^2-10x+12+x-2
$$

$$
color{Brown}5x^4+22x^3-17x^2+21x+10
$$

$$
color{#4257b2}text{(d)} (x^2+7x-2)(x^4+x^3-11x+4)+x^2-x+5
$$

Use distributive property as follows:

$$
x^2(x^4+x^3-11x+4)+7x(x^4+x^3-11x+4)-2(x^4+x^3-11x+4)+x^2-x+5
$$

$$
x^6+x^5-11x^3+4x^2+7x^5+7x^4-77x^2+28x-2x^4-2x^3+22x-8+x^2-x+5
$$

$$
color{Brown}x^6+8x^5+5x^4-13x^3-72x^2+49x-3
$$

$$
text{color{Brown}(a) $color{Brown}x^3+4x^2-51x+89$
\ \
(b) $color{Brown}3x^4-2x^3+3x^2-38x+39$
\ \
(c) $color{Brown}5x^4+22x^3-17x^2+21x+10$
\ \
(d) $color{Brown}x^6+8x^5+5x^4-13x^3-72x^2+49x-3$}
$$

Determine the value of $r$ to make the statement true.

$$
color{#4257b2}text{(a)} (2x-3)(3x+5)+r=6x^2+x+5
$$

Use distributive property for left side as follows:

$$
6x^2-9x+10x-15+r 6x^2+x-15+r
$$

Make a comparison between two sides as follows:

$$
-15+r=5 r=20
$$

$$
color{#4257b2}text{(b)} (x+3)(x+5)+r=x^2+9x-7
$$

Use distributive property for left side as follows:

$$
x^2+3x+5x+5+r x^2+8x+5+r
$$

Make a comparison between two sides as follows:

$$
8x+5+r=9x-7 r=9x-8x-7-5 r=x-12
$$

$$
color{#4257b2}text{(c)} (x+3)(x^2-1)+r=x^3+3x^2-x-3
$$

Use distributive property for left side as follows:

$$
x^3-x+3x^2-3+r x^3+3x^2-x-3+r
$$

Make a comparison between two sides as follows:

$$
r=0
$$

$$
color{#4257b2}text{(d)} (x^2+1)(2x^3-1)+r=2x^5+2x^3+x^2+1
$$

Use distributive property for left side as follows:

$$
2x^5-x^2+2x^3-1+r 2x^5+2x^3-x^2-1+r
$$

Make a comparison between two sides as follows:

$$
-x^2-1+r=x^2+1 r=x^2+1+x^2+1 r=2x^2+2
$$

$$
text{color{Brown} (a) $r=20$ (b) $r=x-12$
\ \
(c) $r=0$ (d) $r=2x^2+2$}
$$

Find the divisor for the following expression.

Note that: Divisor $=$ [Dividend $-$ Reminder] $div$ Quotient

$$
color{#4257b2}text{(a)} (5x^3+x^2+3-123) div5x^2-14x+42
$$

$$
(5x^3+x^2-120) div5x^2-14x+42
$$

Divided the first term for the two question s as follows:

$$
=dfrac{5x^3}{5x^2}=x
$$

Then multiply it $(x)$with $(5x^2-14x+42)$ as follows:

$$
=5x^3-14x^2+42x text{reverse}=-5x^3+14x^2-42x
$$

Subtract the reverse result with $(5x^3+x^2-120)$ as follows:

$$
cancel 5x^3+x^2-120cancel-5x^3+14x^2-42x
$$

$$
15x^2-42x-120
$$

Divided the first term for the two question s as follows:

$$
=dfrac{15x^2}{5x^2}=3
$$

Then multiply it $(3)$with $(5x^2-14x+42)$ as follows:

$$
=15x^2-42x+126 text{reverse}=-15x^2+42x-126
$$

Subtract the reverse result with $(15x^2-42x-120)$ as follows:

$$
cancel 15x^2-42x-120cancel-15x^2+42x-126 =-246
$$

$$
text{Divisor}=(x+1)
$$

Note that: Divisor $=$ [Dividend $-$ Reminder] $div$ Quotient

$$
color{#4257b2}text{(b)} (10x^4-x^2+20x-2-99698) div10x^3-100x^2+999x-9970
$$

$$
(10x^4-x^2+20x-99700) div10x^3-100x^2+999x-9970
$$

Divided the first term for the two question s as follows:

$$
=dfrac{10x^4}{10x^3}=x
$$

Then multiply it $(x)$with $(10x^3-100x^2+999x-9970)$ as follows:

$$
=10x^4-100x^3+999x^2-9970x text{reverse}=-10x^4+100x^3-999x^2+9970x
$$

Subtract the reverse result with $(10x^4-x^2+20x-99700)$ as follows:

$$
cancel 10x^4-x^2+20x-99700cancel-10x^4+100x^3-999x^2+9970x
$$

$$
100x^3-1000x^2+9990-99700
$$

Divided the first term for the two question s as follows:

$$
=dfrac{100x^3}{10x^3}=10
$$

Then multiply it $(10)$with $(10x^3-100x^2+999x-9970)$ as follows:

$$
=100x^3-1000x^2+9990x-99700 text{reverse}=-100x^3+1000x^2-9990x+99700
$$

Subtract the reverse result with $(100x^3-1000x^2+9990-99700)$ as follows:

$$
cancel 100x^3-1000x^2+9990-99700cancel-100x^3+1000x^2-9990x+99700
$$

$$
text{Divisor}=(x+10)
$$

Note that: Divisor $=$ [Dividend $-$ Reminder] $div$ Quotient

$$
color{#4257b2}text{(c)} (x^4+x^3-10x-1-31) div x^3-3x^2+2x-8
$$

$$
(x^4+x^3-10x-32) div x^3-3x^2+2x-8
$$

Divided the first term for the two question s as follows:

$$
=dfrac{x^4}{x^3}=x
$$

Then multiply it $(x)$with $(x^3-3x^2+2x-8)$ as follows:

$$
=x^4-3x^3+2x^2-8x text{reverse}=-x^4+3x^3-2x^2+8x
$$

Subtract the reverse result with $(x^4+x^3-10x-32)$ as follows:

$$
cancel x^4+x^3-10x-32cancel-x^4+3x^3-2x^2+8x
$$

$$
4x^3-2x^2-2x-32
$$

Divided the first term for the two question s as follows:

$$
=dfrac{4x^3}{x^3}=4
$$

Then multiply it $(4)$with $(x^3-3x^2+2x-8)$ as follows:

$$
=4x^3-12x^2+8x-32 text{reverse}=-4x^3+12x^2-8x+32
$$

Subtract the reverse result with $(4x^3-2x^2-2x-32)$ as follows:

$$
cancel 4x^3-2x^2-2x-32cancel-4x^3+12x^2-8x+32 10x^2-10x
$$

$$
text{Divisor}=(x+4)
$$

Note that: Divisor $=$ [Dividend $-$ Reminder] $div$ Quotient

$$
color{#4257b2}text{(d)} (x^3+x^2+7x-7-19) div x^2+3x+13
$$

$$
(x^3+x^2+7x-26) div x^2+3x+13
$$

Divided the first term for the two question s as follows:

$$
=dfrac{x^3}{x^2}=x
$$

Then multiply it $(x)$with $(x^2+3x+13)$ as follows:

$$
=x^3+3x^2+13x text{reverse}=-x^3-3x^2-13x
$$

Subtract the reverse result with $(x^3+x^2+7x-26)$ as follows:

$$
cancel x^3+x^2+7x-26cancel-x^3-3x^2-13x
$$

$$
-2x^2-6x-26
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-2x^2}{x^2}=-2
$$

Then multiply it $(-2)$with $(x^2+3x+13)$ as follows:

$$
=-2x^2-6x-26 text{reverse}=2x^2+6x+26
$$

Subtract the reverse result with $(-2x^2-6x-26)$ as follows:

$$
cancel -2x^2-6x-26cancel2x^2+6x+26
$$

$$
text{Divisor}=(x-2)
$$

$$
text{color{Brown}(a) $x+1$ (b) $x+10$
\ \
(c) $x+4$ (d) $x-2$}
$$

Determine if each binomial is a factor for the following expression or not.

$$
color{#4257b2}text{(a)} x^3+6x^2-x-30 text{divisor}=(x+5)
$$

$(x+5)$ is the factor, so use $(x=-5)$ to divide the equation as follows:

$$
begin{align*}
-5| &=1 6 -1 30
\ \
&= -5 -5 30
\ \
&=1 1 -6 0
end{align*}
$$

$$
x^3+6x^2-x-30=(x+5)(x^2+x-6)
$$

The $(x+5)$ is a factor of expression.

$$
color{#4257b2}text{(b)} x^4-5x^2+4 text{divisor}=(x+2)
$$

$(x+2)$ is the factor, so use $(x=-2)$ to divide the equation as follows:

$$
begin{align*}
-2| &=1 0 -5 0 4
\ \
&= -2 4 2 -4
\ \
&=1 -2 -1 2 0
end{align*}
$$

$$
x^4-5x^2+4=(x+2)(x^3-2x^2-x+2)
$$

The $(x+2)$ is a factor of expression.

$$
color{#4257b2}text{(c)} x^4-5x^2+6 text{divisor}=(x-2)
$$

$(x-2)$ is the factor, so use $(x=2)$ to divide the equation as follows:

$$
begin{align*}
2 &=1 0 -5 0 6
\ \
&= 2 4 -2 -4
\ \
&=1 2 -1 -2 2
end{align*}
$$

The binomial $(x-2)$ is not a factor of expression.

$$
color{#4257b2}text{(d)} 2x^4-x^3-4x^2+2x+1 text{divisor}=(2x-1)
$$

$(2x-1)$ is the factor, so use $(x=0.5)$ to divide the equation as follows:

$$
begin{align*}
0.5 &=2 -1 -4 2 1
\ \
&= 1 0 -2 0
\ \
&=2 0 -4 0 1
end{align*}
$$

The binomial $(2x-1)$ is not a factor of expression.

$$
color{#4257b2}text{(e)} 3x^6+5x^5+9x^2+17x-1 text{divisor}=(3x+5)
$$

$(3x+5)$ is the factor, so use $left(x=-dfrac{5}{3}right)$ to divide the equation as follows:

$$
begin{align*}
dfrac{-5}{3} &=3 5 0 0 9 17 -1
\ \
&= -5 0 0 0 -15 -1
\ \
&=3 0 0 0 0 9 2
end{align*}
$$

The binomial $(3x+5)$ is not a factor of expression.

$$
color{#4257b2}text{(f)} 5x^4-x^3+10x-10 text{divisor}=(5x-1)
$$

$(5x-1)$ is the factor, so use $left(x=dfrac{1}{5}right)$ to divide the equation as follows:

$$
begin{align*}
dfrac{1}{5} &=5 -1 0 10 -10
\ \
&= 1 0 0 2
\ \
&=5 0 0 10 -8
end{align*}
$$

The binomial $(2x-1)$ is not a factor of expression.

$$
text{color{Brown} (a) $x+5$, is a factor (b) $x+2$ is a factor
\ \
(c) $x-2$ is not a factor (d) $2x-1$ is not a factor
\ \
(d) $3x+5$ is not a factor (f) $5x-1$ is not a factor}
$$

Find the height of rectangle that has a volume $x^3+6x^2+11x+6$ and has a long $x+3$ and wide $x+2$

use theorem division to get the height as follows:

$(x+3)$ is the factor, so use $(x=-3)$ to divide the equation as follows:

$$
begin{align*}
-3| &=1 6 11 6
\ \
&= -3 -9 -6
\ \
&=1 3 2 0
end{align*}
$$

$$
x^3+6x^2+11x+6=(x+3)(x^2+3x+2)
$$

$(x+2)$ is the factor, so use $(x=-2)$ to divide the equation $(x^2+3x+2)$as follows:

$$
begin{align*}
-2| &=1 3 2
\ \
&= -2 -2
\ \
&=1 1 0
end{align*}
$$

$$
x^3+6x^2+11x+6=(x+3)(x+2)(x+1)
$$

The height of rectangle is $(x+1)$

$$
text{color{Brown} Height $(x+1)$}
$$

$$
text{color{#4257b2}(a) Find the value of $P$ if polynomial $8x^3+10x^2-Px-5$ has a factor of \ text{ } $(2x+1)$ and there is no reminder.}
$$

Substitute the value of $x=-dfrac{1}{2}$ for the polynomial as follows:

$$
begin{align*}
&8left(-dfrac{1}{2}right)^3+10left(-dfrac{1}{2}right)^2-Pleft(-dfrac{1}{2}right)-5=0
\ \
&8left(-dfrac{1}{8}right)+10left(dfrac{1}{4}right)-Pleft(-dfrac{1}{2}right)-5=0
\ \
& -1+ dfrac{10}{4}-5 = -dfrac{1}{2} P
\ \
& -dfrac{1}{2} P= -dfrac{7}{2}
\ \
& -dfrac{1}{2} P=-3.5
\ \
&text{Multiply both sides by $-2$:}
\ \
&therefore P=7
end{align*}
$$

$$
text{color{#4257b2}(b) Find the value of $k$ if polynomial $x^6+x^4-2x^2+K$ has a factor of \ text{ } $(x^2+1)$
and the reminder is $5$.}
$$

$$
x^2+1=0 rightarrow x^2=-1
$$

$$
f(x)=text{divisor}times text{quotient}+text{reminder}
$$

$$
f(x)=(x^2+1)+5
$$

Substitute the value of $x^2=-1$ for the function as follows:

$$
f(x)=-1+1+5 rightarrow f(x)=5
$$

$$
begin{align*}
&(x^2)^3+(x^2)^2-2x^2+K=5
\ \
&(-1)^3+(-1)^2-2(-1)+K=5
\ \
&-1+1+2+K=5
\ \
&K+2=5
\ \
therefore &K=3
end{align*}
$$

(a) $P=7$ (b) $K=3$

Find the value of $p$ if polynomial $x^3+Px^2-x-2$ has a factor of $(x-1)$

Substitute the value of $x=1$ for the polynomial as follows:

$$
(1)^3+P(1)^2-1-2=0 1+P-1-2=0
$$

$$
P-2=0 P=2
$$

$$
text{color{Brown} $P=2$}
$$

Is $x^n-1$always divisible by $(x-1)$ where $(nge1)$?

$because (nge1)$ and its integer number

$therefore $The function may have divisible by $(x-1)$

$$
text{color{Brown} The function may have divisible by $(x-1)$}
$$

Answer for the following questions

$$
text{(a) Write the division statement}
$$

divisor$=(x-4)$ quotient$=(x^2+x-6)$ reminder$=7$

$f(x)=$ divisor$cdot$quotient + reminder

$$
f(x)=(x-4)(x^2+x-6)+7
$$

$$
f(x)=x^3+x^2-6x-4x^2-4x+24+7
$$

$$
f(x)=x^3-3x^2-10x+31
$$

$$
text{(b) Factor the division statement}
$$

$$
f(x)=(x-4)(x^2+x-6)+7
$$

$$
f(x)=(x-4)(x+3)(x-2)+7
$$

$$
text{(c) Graph the division statement}
$$

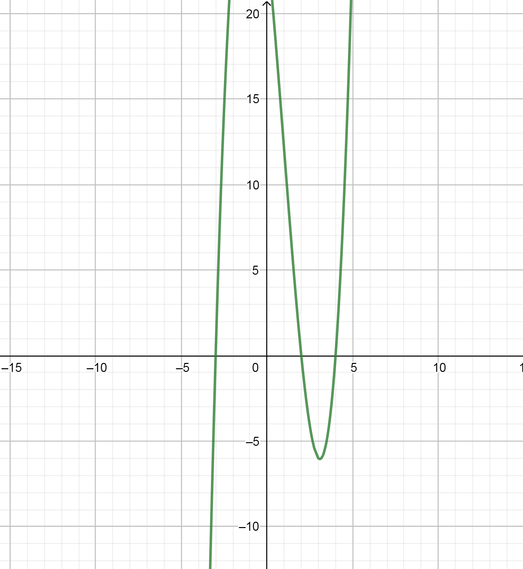
$$
text{color{Brown}(a) $f(x)=x^3-3x^2-10x+31$
\ \
(b) $f(x)=(x-4)(x+3)(x-2)+7$}
$$

$$
text{color{#4257b2}Use an example to show how the synthetic division is essentially the same as regular polynomial division.}
$$

$$
text{color{#c34632}Division by using regular polynomial division}
$$

$$
(3x^3-5x^2+1) text{by} (x-4)
$$

Divided the first term of the equation as follows:

$$
=dfrac{x^3}{x}=x^2
$$

Then multiply it $(x^2)$with $(x-4)$ as follows:

$$
=x^3-4x^2 text{reverse}=-x^3+4x^2
$$

Subtract the reverse result with $(x^3-2x+1)$ as follows:

$$
cancel x^3-2x+1cancel-x^3+4x^2 4x^2-2x+1
$$

Divided the first term for the two question s as follows:

$$
=dfrac{4x^2}{x}=4x
$$

Then multiply it $(4x)$with $(x-4)$ as follows:

$$
=4x^2-16x text{reverse}=-4x^2+16x
$$

Subtract the reverse result with $(4x^2-2x+1)$ as follows:

$$
cancel4x^2-2x+1cancel-4x^2+16x=0
$$

$$
14x+1
$$

Divided the first term for the two question s as follows:

$$
=dfrac{14x}{x}=14
$$

Then multiply it $(14)$with $(x-4)$ as follows:

$$
=14x-56 text{reverse}=-14x+56
$$

Subtract the reverse result with $(14x+1)$ as follows:

$$
cancel14x+1cancel-14x+56=0 =57
$$

$$
(x^3-2x+1)=(x-4)(x^2+4x+14)+57
$$

$$
text{color{#c34632} Division by synthetic division}
$$

$$
x^3-2x+1 text{by} (x-4)
$$

Use $(x=4)$ to divide the equation as follows:

$$
begin{align*}
4| &=1 0 -2 1
\ \
&= 4 16 56
\ \
&=1 4 14 57
end{align*}
$$

$$
x^3-2x+1=(x-4)(x^2+4x+14)+57
$$

{$text{color{Brown}Since the results in two methods are equals, so the synthetic division is essentially the same as regular polynomial division}$

{$text{color{Brown} Result by synthetic division is, $ x^3-2x+1=(x-4)(x^2+4x+14)+57$
\ \
Result by regular division is, $ x^3-2x+1=(x-4)(x^2+4x+14)+57$
\ \
Since the results in two methods are equals, so the synthetic division is essentially the same as regular polynomial division}$

What the radius of cylinder that has a volume $(4pi x^3+28pi x^2+65pi x+50pi)$ and its height is $(x+2)$

Volume of cylinder can be represent by $(pi r^2 h)=pi r^2 (x+2)$

Divide the volume of can by height to get the square of radius as follows:

$$
4pi x^3+28pi x^2+65pi x+50pidiv(x+2)
$$

$$
begin{align*}
-2| &=4pi 28pi 65pi 50pi
\ \
&= -8pi -40pi -50pi
\ \
&=4pi 20pi 25pi 0
end{align*}
$$

$$
pi r^2=(x+2)(4pi x^2+20pi x+25pi)
$$

$$
pi r^2=pi (x+2)(4x^2+20x+25)
$$

Divide both of sides by $pi$ as follows:

$$
r^2=(x+2)(2x+5)^2
$$

Use square root property as follows:

$$
sqrt{r^2}=sqrt{(x+2)(2x+5)^2}
$$

$$
r=(2x+5)sqrt{(x+2)}
$$

$$
text{color{Brown}$$r=(2x+5)sqrt{(x+2)}$$}
$$

Divided function (a) $color{#4257b2}(x^4+x^3y-xy^3-y^4)$ by $color{#4257b2}(x^2-y^2)$

Divided the first term for the two question s as follows:

$$
=dfrac{x^4}{x^2}=x^2
$$

Then multiply it $(x^2)$with $(x^2-y^2)$ as follows:

$$
=x^4-x^2y^2 text{reverse}=-x^4+x^2y^2
$$

Subtract the reverse result with $(x^4+x^3y-xy^3-y^4)$ as follows:

$$
cancel x^4+x^3y-xy^3-y^4cancel-x^4+x^2y^2
$$

$$
x^3y+x^2y^2-xy^3-y^4
$$

Divided the first term for the two question s as follows:

$$
=dfrac{x^3y}{x^2}=xy
$$

Then multiply it $(xy)$with $(x^2-y^2)$ as follows:

$$
=x^3y-xy^3 text{reverse}=-x^3y+xy^3
$$

Subtract the reverse result with $(x^3y+x^2y^2-xy^3-y^4)$ as follows:

$$
cancel x^3y+x^2y^2-xy^3-y^4cancel-x^3y+xy^3=0
$$

$$
x^2y^2-y^4
$$

Divided the first term for the two question s as follows:

$$
=dfrac{x^2y^2}{x^2}=y^2
$$

Then multiply it $(y^2)$with $(x^2-y^2)$ as follows:

$$
=x^2y^2-y^4 text{reverse}-x^2y^2+y^4
$$

Subtract the reverse result with $(x^2y^2-y^4)$ as follows:

$$
cancel x^2y^2-y^4cancel-x^2y^2+y^4=0
$$

$$
(x^4+x^3y-xy^3-y^4)=(x^2-y^2)(x^2+xy+y^2)
$$

Divided function (b) $color{#4257b2}(x^4-2x^3y+2x^2y^2-2xy^3+y^4)$ by $color{#4257b2}(x^2+y^2)$

Divided the first term for the two question s as follows:

$$
=dfrac{x^4}{x^2}=x^2
$$

Then multiply it $(x^2)$with $(x^2+y^2)$ as follows:

$$
=x^4+x^2y^2 text{reverse}=-x^4-x^2y^2
$$

Subtract the reverse result with $(x^4-2x^3y+2x^2y^2-2xy^3+y^4)$ as follows:

$$
cancel x^4-2x^3y+2x^2y^2-2xy^3+y^4cancel-x^4-x^2y^2
$$

$$
-2x^3y+x^2y^2-2xy^3+y^4
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-2x^3y}{x^2}=-2xy
$$

Then multiply it $(-2xy)$with $(x^2+y^2)$ as follows:

$$
=-2x^3y-2xy^3 text{reverse}=2x^3y-2xy^3
$$

Subtract the reverse result with $(-2x^3y+x^2y^2-2xy^3+y^4)$ as follows:

$$
cancel -2x^3y+x^2y^2-2xy^3+y^4cancel2x^3y-2xy^3=0
$$

$$
x^2y^2-4xy^3+y^4
$$

Divided the first term for the two question s as follows:

$$
=dfrac{x^2y^2}{x^2}=y^2
$$

Then multiply it $(y^2)$with $(x^2+y^2)$ as follows:

$$
=x^2y^2+y^4 text{reverse}-x^2y^2-y^4
$$

Subtract the reverse result with $(x^2y^2-4xy^3+y^4)$ as follows:

$$
cancel x^2y^2-4xy^3+y^4cancel-x^2y^2-y^4=0
$$

$$
-4xy^3
$$

$$
(x^4-2x^3y+2x^2y^2-2xy^3+y^4)=(x^2+y^2)(x^2-2xy+y^2)-4xy^3
$$

$$
text{color{Brown}(a) $(x^2-y^2)(x^2+xy+y^2)$
\ \
(b) $(x^2+y^2)(x^2-2xy+y^2)-4xy^3$}
$$

If the $x-y$ the factor of $x^3-y^3$

Standard form is $a^3-b^3=(a-b)(a^2+ab+b^2)$

$$
x^3-y^3=(x-y)(x^2+xy+y^2)
$$

The term of $(x-y)$ is a factor of $x^3-y^3$

$$
text{color{Brown}$$x^3-y^3=(x-y)(x^2+xy+y^2)$$}
$$

$$
text{color{#4257b2}If $f(x)=(x+5)q (x)+(x+3)$, what is the first multiple of $(x+5)$ that is greater than $f(x)$}
$$

Assume that $q(x)=x$, then substitute different values of $(x)$ till be the $q(x)$ is greater than $f(x)$ as follows:

$$
color{#4257b2}text{At} x=1
$$

$$
q(x)=x q(x)=1
$$

$$
f(x)=(x+5)q(x)+(x+3) f(x)=(1+5)(1)+(1+3)
$$

$$
f(x)=(6cdot1)+4 f(x)=10
$$

$because q(x)<f(x) therefore x=1$, not allowable

$$
color{#4257b2}text{At} x=0
$$

$$
q(x)=x q(x)=0
$$

$$
f(x)=(x+5)q(x)+(x+3) f(x)=(0+5)(0)+(0+3)
$$

$$
f(x)=(5cdot0)+3 f(x)=3
$$

$because q(x)<f(x) therefore x=0$, not allowable

$$
color{#4257b2}text{At} x=-1
$$

$$
q(x)=x q(x)=-1
$$

$$
f(x)=(x+5)q(x)+(x+3) f(x)=(-1+5)(-1)+(-1+3)
$$

$$
f(x)=(4cdot-1)+2 f(x)=-2
$$

$because q(x)>f(x) therefore x=-1$, is allowable
$$
color{#4257b2}text{At} x=-1
$$

$$
text{color{Brown}$q(x)$ is greater than $f(x)$ at value of $(x=-1)$}
$$