Match the equations with matched figure.

$$
color{#4257b2}text{(a)} f(x)=2(x+1)^2(x-3)
$$

The higher degree is $(3)$, so this is cubic equation.

The leading coefficient is positive, so the function is upward.

The zeros of the functions are$(-1, 3)$ Figure$(C)$

$$
color{#4257b2}text{(b)} f(x)=2(x+1)^2(x-3)^2
$$

The higher degree is $(4)$, so this is quartic equation.

The leading coefficient is positive, so the function is upward.

The zeros of the functions are$(-1, 3)$ Figure$(A)$

$$
color{#4257b2}text{(c)} f(x)=-2(x+1)(x-3)^2
$$

The higher degree is $(3)$, so this is cubic equation.

The leading coefficient is negative, so the function is downward.

The zeros of the functions are$(-1, 3)$ Figure$(B)$

$$
color{#4257b2}text{(d)} f(x)=x(x+1)(x-3)(x-5)
$$

The higher degree is $(4)$, so this is quadrtic equation.

The leading coefficient is positive, so the function is upward.

The zeros of the functions are$(-1, 3, 5)$ Figure$(D)$

$$
text{color{Brown}(a) Figure$(C)$ (b) Figure$(A)$
\ \
(c) Figure$(B)$ (d) Figure$(D)$}
$$

Sketch the following functions.

$$
text{(a)} -(x-4)(x-1)(x+5)
$$

Use distributive property as follows:

$$
(4-x)(x^2+4x-5)
$$

$$
4(x^2+4x-5)-x(x^2+4x-5)
$$

$$
4x^2+16x-20-x^3-4x^2+5x
$$

Rearrange the tiles to group like terms as follows:

$$
-x^3+21x-20
$$

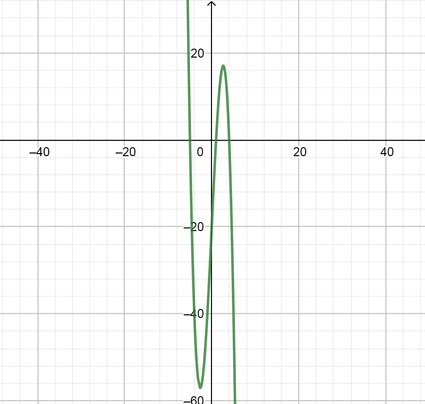
$$
text{(b)} x^2(x-6)^3
$$

$$
x^2(x-6)(x-6)^2
$$

Use distributive property as follows:

$$
x^3-6x^2(x^2-12x+36)
$$

$$
x^3(x^2-12x+36)-6x^2(x^2-12x+36)
$$

$$
x^5-12x^4+36x^3-6x^4+72x^3-216x^2
$$

Rearrange the tiles to group like terms as follows:

$$
x^5+(-12x^4-6x^4)+(36x^3+72x^3)-216x^2
$$

$$
x^5-18x^4+108x^3-216x^2
$$

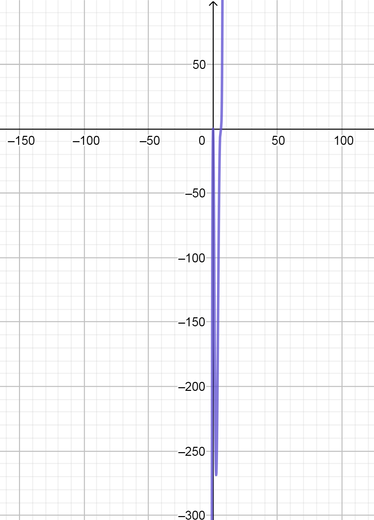
$$
text{color{Brown}See sketches}
$$

The quadratic function that have zeros at $x=-1, x=4$, answer for the following question.

$$
text{color{#4257b2}(a) Write the equation of the family, then state two functions belongs to the family.}
$$

$$
x=-1 x=4
$$

Standard equation is $y=(x+x_{1})(x+x_{2})$

$$
y=(x+1)(x-4)
$$

The other function that belongs to the family are:

$$
y=(x-4)^2 y=(x+1)^2
$$

$$
text{color{#4257b2}(b) Determine the function that belongs to the family and passes through the point $(5, 9)$, then graph the equation.}
$$

Standard function is $y=a(x+x_{1})(x+x_{2})$

Substitute the value of $x=5, y=9$ as follows:

$$
9=a(5+1)(5-4) 9=a(6cdot1) 9=6a
$$

$$
a=dfrac{9}{6} a=dfrac{3}{2}
$$

$$
f(x)=dfrac{3}{2}(x+1)(x-4)
$$

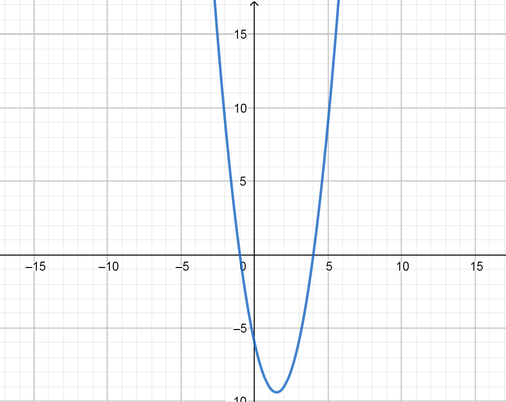
$$
text{color{Brown}(a) $f(x)=(x+1)(x-4)$
\ \
(b) $f(x)=dfrac{3}{2}(x+1)(x-4)$}
$$

Write the equation for the figure in text book.

$$
text{color{#4257b2} (a) First figure}
$$

The function is upward, so the leading function is positive.

The degree of function is $(3)$ cubic function.

The function cross $x$ axis at point [-3, 2, 5]

$$
f(x)=a(x+3)(x-2)(x-5)
$$

Use point $(1, 8)$ to get the value of $a$ as follows:

$$
8=a(1+3)(1-2)(1-5) 8=a(4cdot-1cdot-4)
$$

$$
8=acdot16 a=dfrac{8}{16} a=dfrac{1}{2}
$$

$$
f(x)=dfrac{1}{2} (x+3)(x-2)(x-5)
$$

$$
text{color{#4257b2} (b) Second figure}
$$

The function is downward, so the leading function is negative.

The degree of function is $(4)$ quartic function.

The function cross $x$ axis at point [-1, 2, 4]

$$
f(x)=-ax(x+1)(x-2)(x-4)
$$

Use point $(1, -12)$ to get the value of $a$ as follows:

$$
-12=-a(1+1)(1-2)(1-4) -12=-a(2cdot-1cdot-3)
$$

$$
-12=-acdot6 a=dfrac{-12}{-6} a=2
$$

$$
f(x)=-2 x (x+1)(x-2)(x-4)
$$

$$
text{color{Brown}(a) $f(x)=tfrac{1}{2} (x+3)(x-2)(x-5)$
\ \
(b) $f(x)=-2 x (x+1)(x-2)(x-4)$}
$$

Organize the following expression into their families.

$$
color{#4257b2}text{(a)} y=2(x-3)(x+5)
$$

$$
y=2(x^2-3x+5x-15) =2(x^2+2x-15)
$$

$$
y=2x^2+4x-30
$$

$$
color{#4257b2}text{(b)} y=-1.8(x-3)^2(x+5)
$$

$$
y=-1.8(x^2-6x+4)(x+5) =-1.8(x^3-6x^2+4x+5x^2-30x+20)
$$

$$
y=-1.8(x^3-x^2-26x+20)
$$

$$
color{#4257b2}text{(c)} y=-x(x+6)(x+8)
$$

$$
y=-x(x^2+6x+8x+48) y=-x(x^2+14x+48)
$$

$$
y=-x^3-14x^2-48x
$$

$$
color{#4257b2}text{(d)} y=2(x+5)(x+3)^2
$$

$$
y=2(x^2+6x+9)(x+5) y=2(x^3+6x^2+9x+5x^2+30x+45)
$$

$$
y=2(x^3+11x^2+39x+45)
$$

$$
color{#4257b2}text{(e)} y=(x-3)^2(x+5)
$$

$$
y=(x^2-6x+9)(x+5) y=x^3-6x^2+9x+5x^2-30x+45
$$

$$
y=x^3-x^2-21x+45
$$

$$
color{#4257b2}text{(f)} y=x(x+6)(x+8)
$$

$$
y=x(x^2+6x+8x+48) y=x(x^2+14x+48)
$$

$$
y=x^3+14x^2+48x
$$

$$
color{#4257b2}text{(g)} y=dfrac{1}{2}(x-3)(x+3)
$$

$$
y=dfrac{1}{2}(x^2-9)
$$

$$
color{#4257b2}text{(h)} y=-5(x+8)(x)(x+6)
$$

$$
y=-5x(x^2+6x+8x+48) y=-5x(x^2+14x+48)
$$

$$
y=-5x^3-70x^2+240x
$$

$$
color{#4257b2}text{(i)} y=(x-3)(x+5)
$$

$$
y=x^2-3x+5x-15
$$

$$
y=x^2+2x-15x
$$

$$
color{#4257b2}text{(j)} y=dfrac{3}{5}(x+5)(x+3)^2
$$

$$
y=dfrac{3}{5}(x+5)(x^2+6x+9) y=dfrac{3}{5}(x^3+6x^2+9x+5x^2+30x+45)
$$

$$
y=dfrac{3}{5}(x^63+11x^2+39x+45)
$$

$$
color{#4257b2}text{(k)} y=dfrac{1}{4}x(x+6)(x+8)
$$

$$
y=dfrac{1}{4}x(x^2+6x+8x+48) y=dfrac{1}{4}x(x^2+14x+48)
$$

$$
y=dfrac{1}{4}(x^3+14x^2+48x)
$$

$$
color{#4257b2}text{(l)} y=2(x+5)(x^2+6x+9)
$$

$$
y=2(x^3+6x^2+9x+5x^2+30x+45)
$$

$$
y=2(x^3+11x^2+39x+45)
$$

$$
text{color{Brown}(a) $y=2x^2+4x-30$
\ \
(b) $y=-1.8(x^3-x^2-26x+20)$
\ \
(c) $y=-x^3-14x^2-48x$
\ \
(d) $y=2(x^3+11x^2+39x+45)$
\ \
(e) $y=x^3-x^2-21x+45$
\ \
(f) $y=x^3+14x^2+48x$
\ \
(g) $y=dfrac{1}{2}(x^2-9)$
\ \
(h) $y=-5x^3-70x^2+240x$
\ \
(i) $y=x^2+2x-15x$
\ \
(j) $y=dfrac{3}{5}(x^63+11x^2+39x+45)$
\ \
(k) $y=dfrac{1}{4}(x^3+14x^2+48x)$
\ \
(l) $y=2(x^3+11x^2+39x+45)$}
$$

Graph the following function.

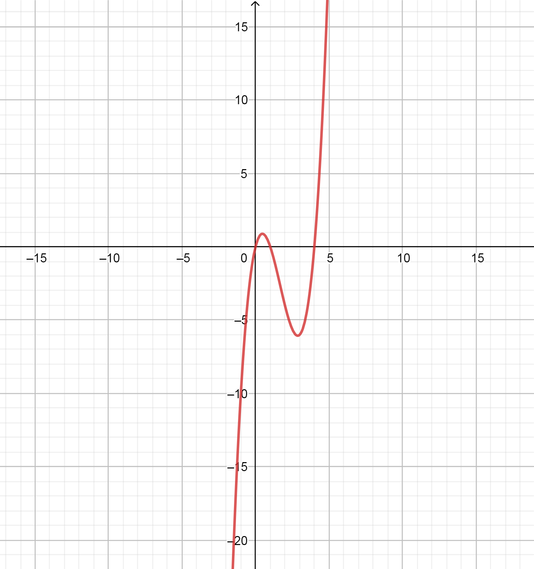
$$
text{(a)} x(x-4)(x-1)
$$

Graph the following function.

$$
text{(b)} -(x-1)(x+2)(x-3)
$$

Graph the following function.

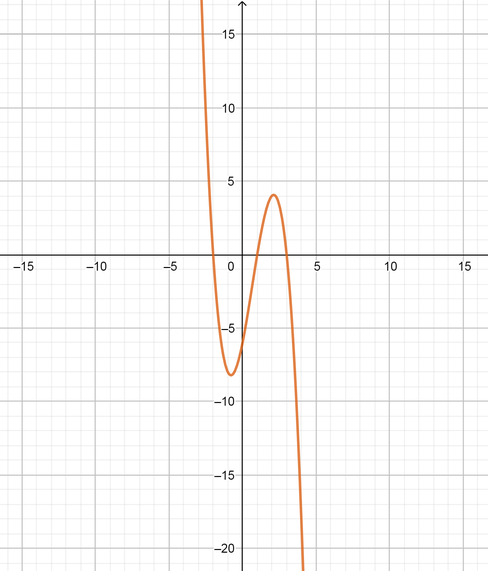
$$
text{(c)} x(x-3)^2
$$

Graph the following function.

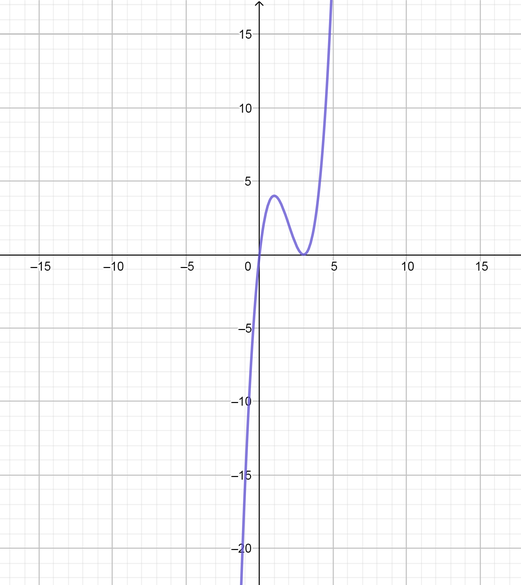
$$
text{(d)} (x+1)^3
$$

Graph the following function.

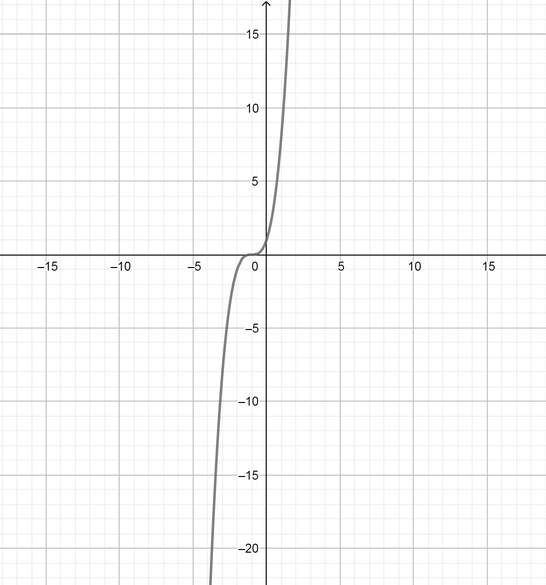
$$
text{(e)} x(2x+1)(x-3)(x-5)
$$

Graph the following function.

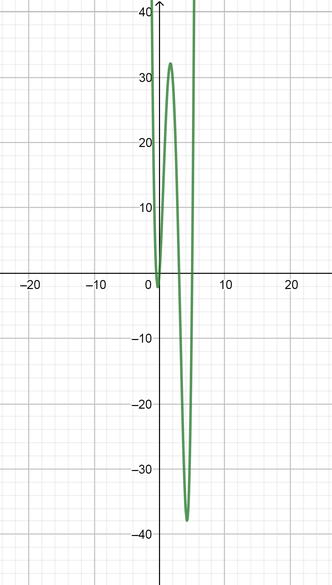
$$
text{(a)} x^2(3x-2)^2
$$

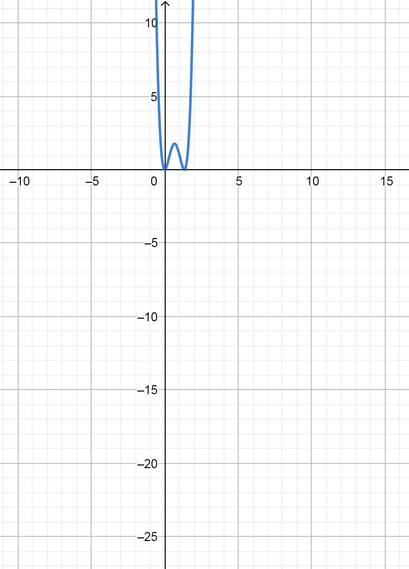
$$
text{color{Brown}See graphs}
$$

Sketch the cubic function that have the following zeros.

$$
color{#4257b2}text{(a)} -3, 0, 2
$$

Standard function is $y=(x+x_{1})(x+x_{2})(x+x_{3})$

$$
y=x (x+3)(x-2)
$$

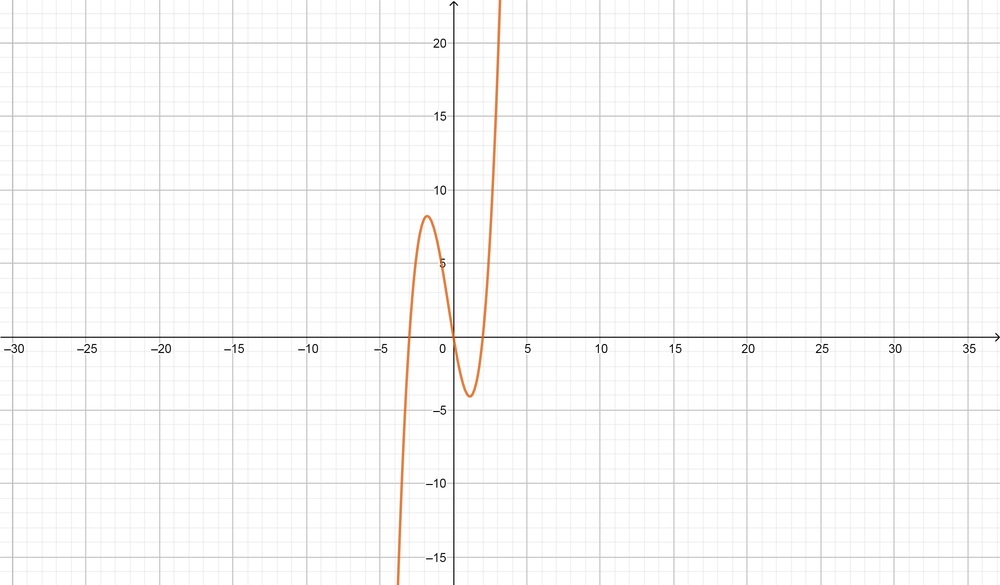
$$
color{#4257b2}text{(b)} -1, 4, 4
$$

Standard function is $y=(x+x_{1})(x+x_{2})(x+x_{3})$

$$
y=(x+1)(x-4)(x-4)
$$

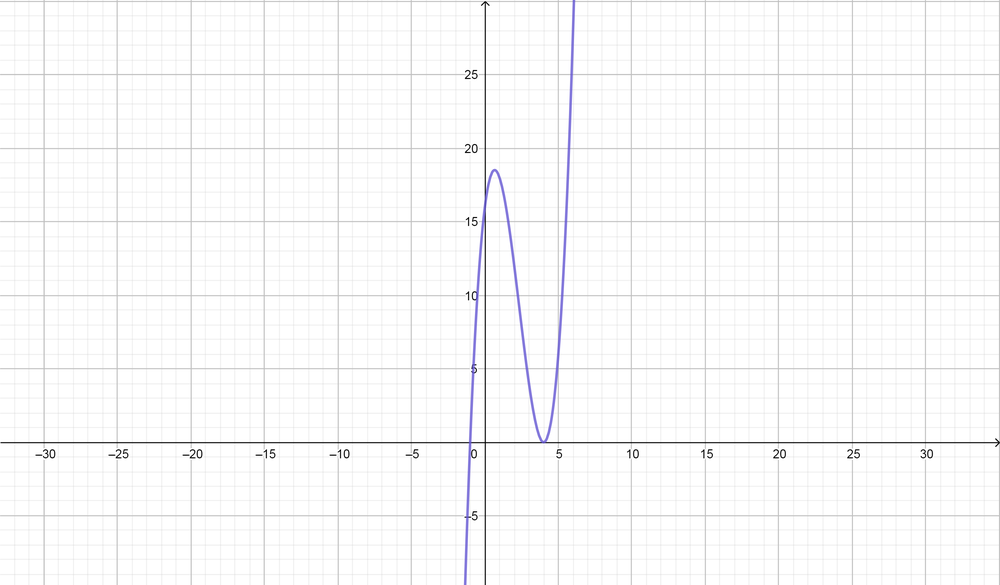
$$
color{#4257b2}text{(c)} -2, -2, -2
$$

Standard function is $y=(x+x_{1})(x+x_{2})(x+x_{3})$

$$
y=(x+2)(x+2)(x+2)
$$

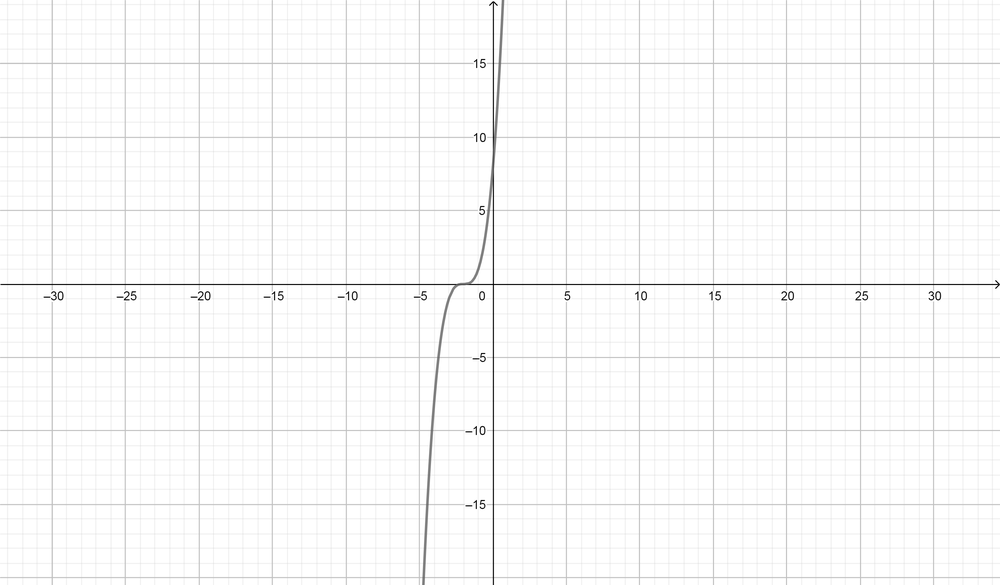
$$
color{#4257b2}text{(d)} 3, -dfrac{1}{2}, -dfrac{1}{2}
$$

Standard function is $y=(x+x_{1})(x+x_{2})(x+x_{3})$

$$
y=left(x+dfrac{1}{2}right)left(x+dfrac{1}{2}right)(x-3)
$$

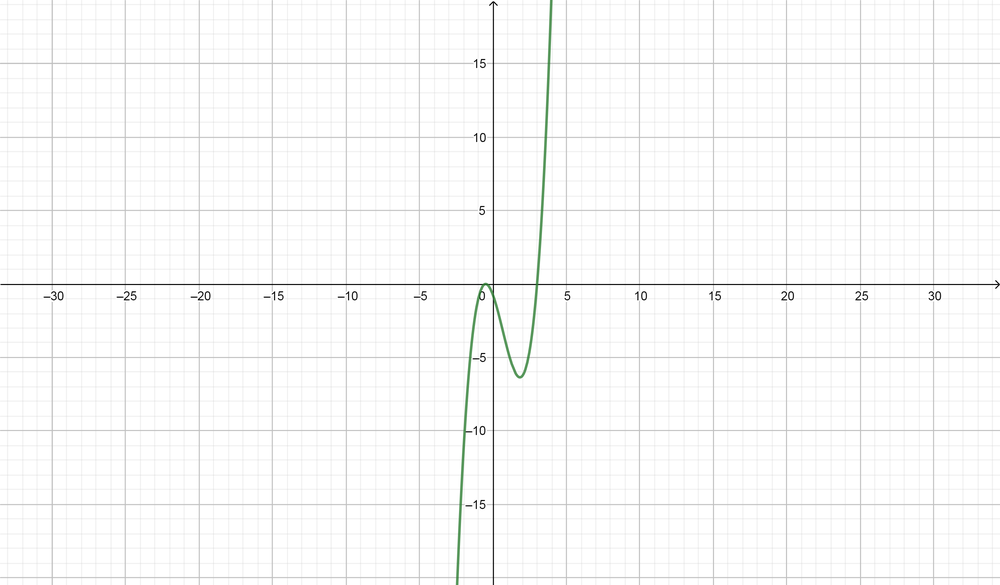
$$
text{color{Brown}See graphs}
$$

Graph and write the quartic function with following zeros.

$$
color{#4257b2}text{(a)} -5, -3, 2, 4
$$

Standard function is $y=(x+x_{1})(x+x_{2})(x+x_{3})(x+x_{4})$

$$
y=(x+5)(x+3)(x-2)(x-4)
$$

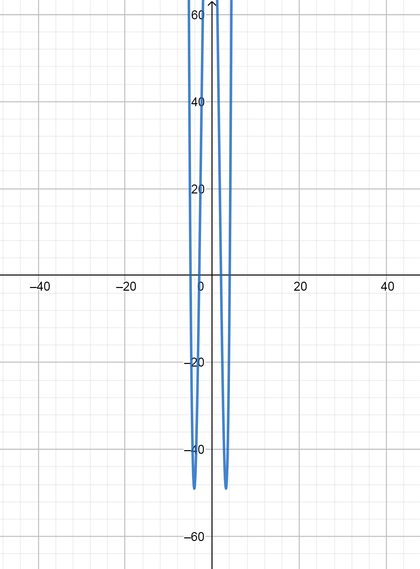
$$
color{#4257b2}text{(b)} -2, -2, 3, 3
$$

Standard function is $y=(x+x_{1})(x+x_{2})(x+x_{3})(x+x_{4})$

$$
y=(x+2)(x+2)(x-3)(x-3)
$$

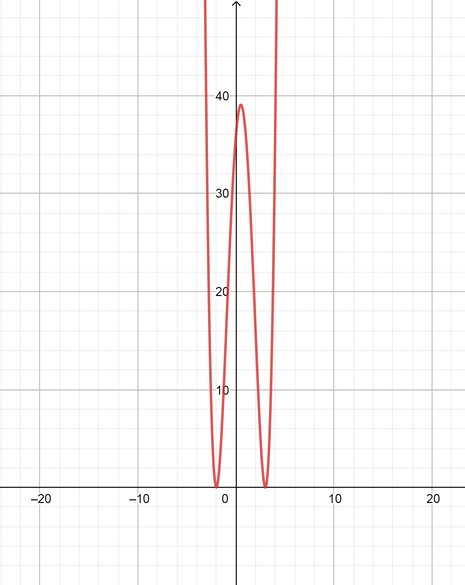
$$
color{#4257b2}text{(c)} -5, dfrac{3}{4}, 5, 5
$$

Standard function is $y=(x+x_{1})(x+x_{2})(x+x_{3})(x+x_{4})$

$$
y=left(x-dfrac{3}{4}right)(x+2)(x-5)(x-5)
$$

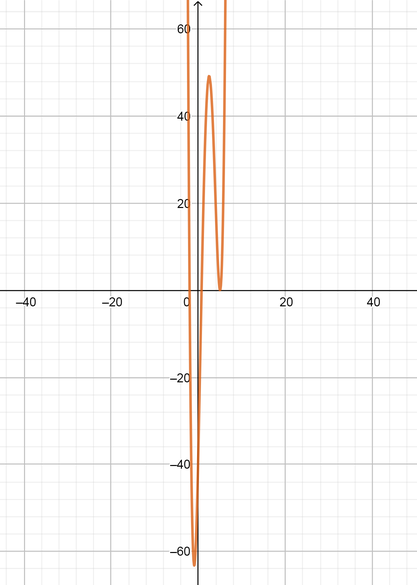
$$
color{#4257b2}text{(d)} 6, 6, 6, 6
$$

Standard function is $y=(x+x_{1})(x+x_{2})(x+x_{3})(x+x_{4})$

$$
y=(x-6)(x-6)(x-6)(x-6)
$$

Write two function that belongs to the family.

$$
x^4-5x^2+4 5x^4-x^3+10x-10
$$

$$
text{color{Brown}(a) See sketches.
\ \
(b) $x^4-5x^2+4 5x^4-x^3+10x-10$}
$$

Sketch the graph for the following function.

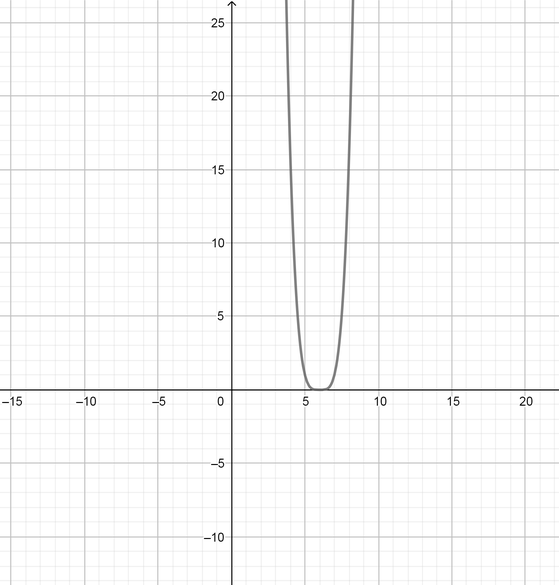
$$
color{#4257b2}text{(a)} y=3x^3-48x
$$

$$
y=3x(x^2-16)
$$

$$
y=3x(x+4)(x-4)
$$

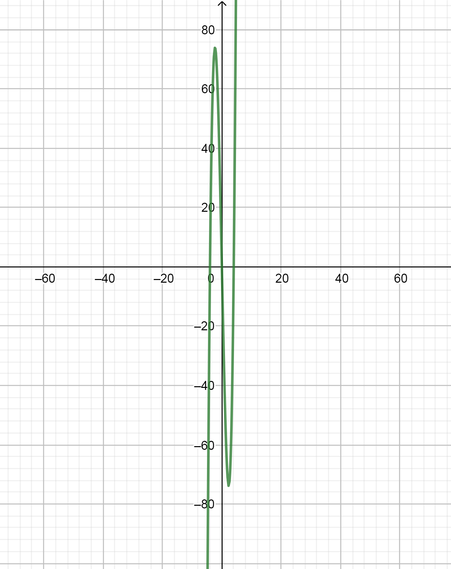
$$
color{#4257b2}text{(b)} y=x^4+4x^3+4x^2
$$

$$
y=x^2(x^2+4x+4)
$$

$$
y=x^2(x+2)^2
$$

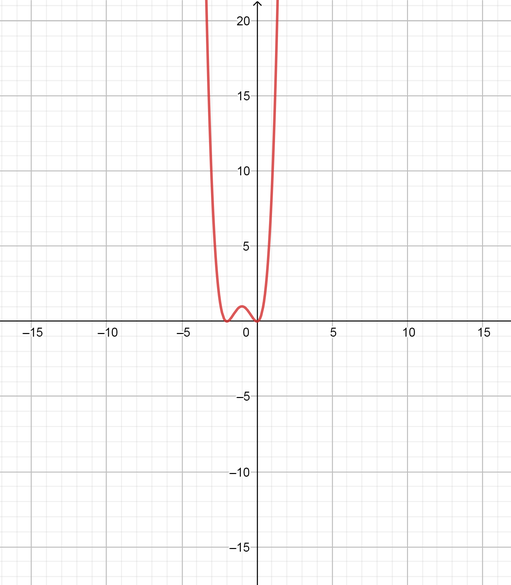
$$
color{#4257b2}text{(c)} y=x^3-9x^2+27x-27
$$

$$
y=(x-3)^3
$$

$$
y=(x-3)(x-3)^2
$$

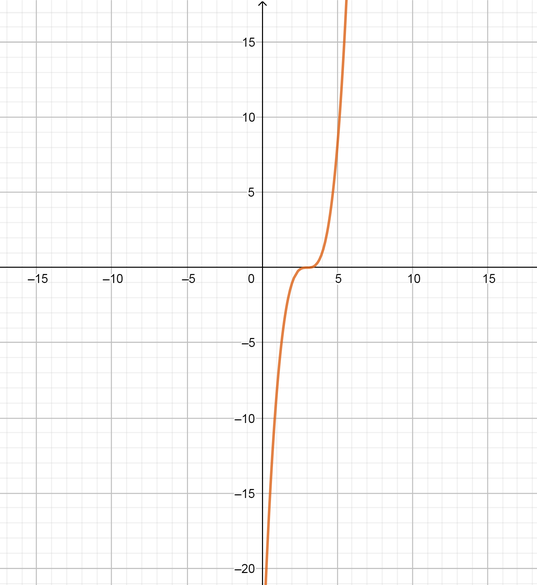
$$
color{#4257b2}text{(d)} y=-x^4-15x^3-75x^2-125x
$$

$$
y=-x(x^3+15x^2+75x+125)
$$

$$
y=-x(x+5)^3
$$

$$
text{color{Brown}See sketches}
$$

Sketch a graph of the polynomial function that represent the following condition.

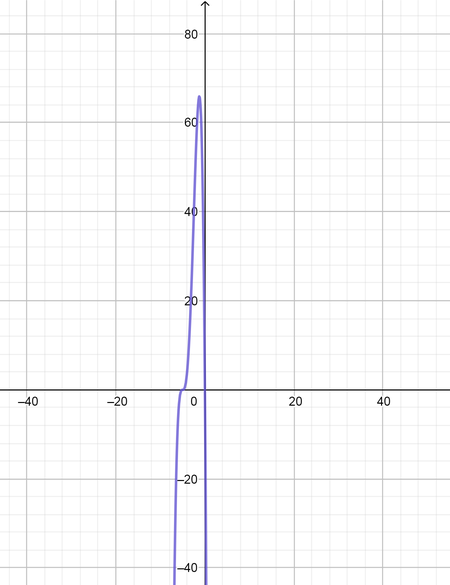
$$
text{color{#4257b2}[a] $(4)$ Degree, positive leading coefficient, $(3)$ zeros, $(3)$ turning points.}
$$

$$
f(x)=(x-1)^2(x+1)(x+3)
$$

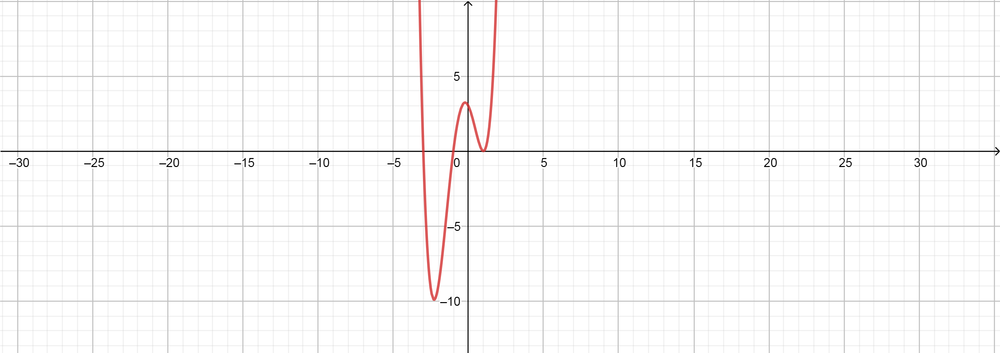
$$
text{color{#4257b2}[b] $(4)$ Degree, negative leading coefficient, $(2)$ zeros, $(1)$ turning points.}
$$

$$
f(x)=-(x^2-1)(x^2+1)
$$

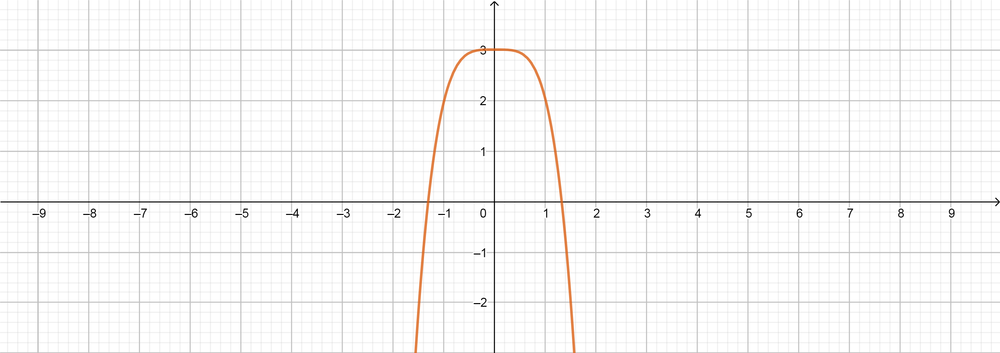
$$
text{color{#4257b2}[c] $(4)$ Degree, positive leading coefficient, $(2)$ zeros, $(3)$ turning points.}
$$

$$
f(x)=(x-1)^2(x+1)^2
$$

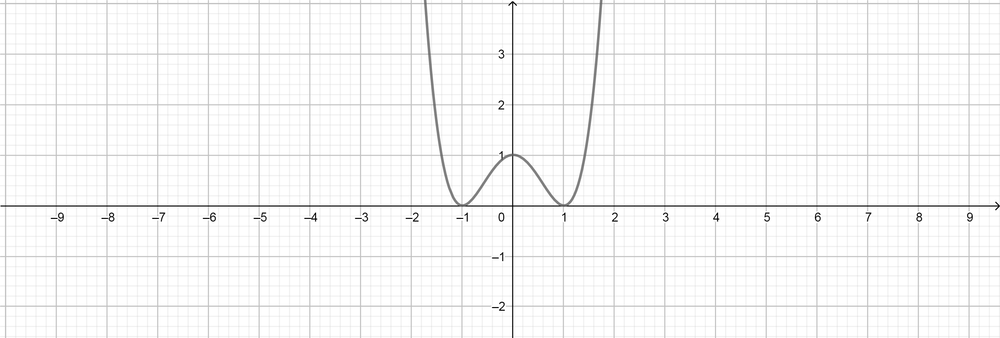
$$
text{color{#4257b2}[d] $(3)$ Degree, negative leading coefficient, $(1)$ zeros, no turning points.}
$$

$$
f(x)=-(x-2)^3
$$

$$
text{color{Brown} See graphs}
$$

Company profits and losses during $(15)$ years period are shown in the table attached in the textbook.

$$
text{color{#4257b2}(a) Sketch the graph of the data points in the table using the year of $(1990)$ as the values of the independent variables.}
$$

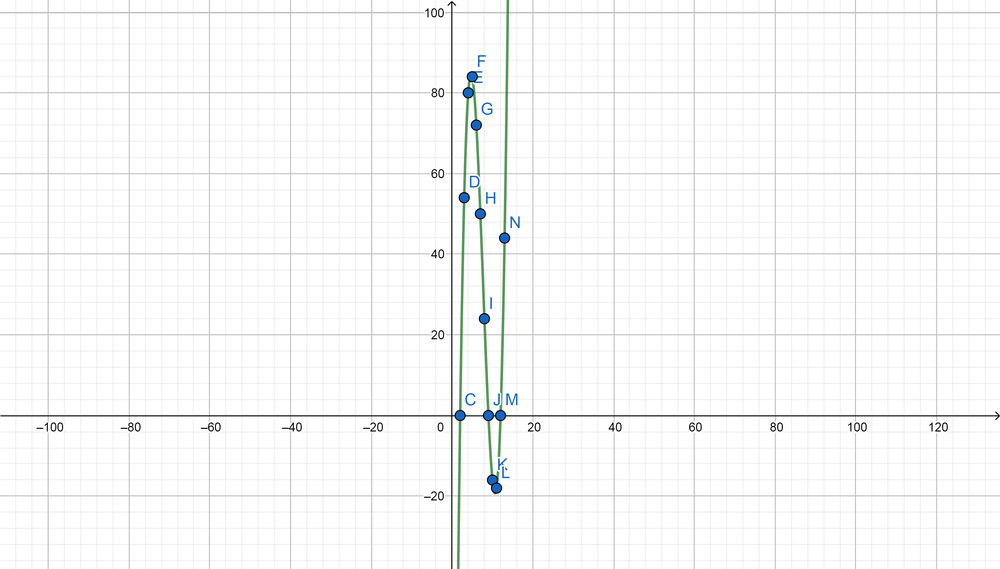
$$
text{color{#4257b2}(b) If $(x)$ represent the number of years since $(1990)$, write the polynomial equation that represent these data.}
$$

From the graph the curve represent the cubic function and crosses with $(x)$ axis at three points (zeros) which equal $(x=2 x=9 x=12)$, so use standard formula for cubic function as follows:

$$
f(x)=a (x-x_{1})+(x-x_{2})+(x-x_{3})
$$

Substitute the values of $(x)$ as follows:

$$
f(x)=a (x-2)(x-9)(x-12)
$$

From table in the textbook, use point of $(x, y)$ to get the value of $(a)$ as follows:

Substitute the values of $(x=3, y=54)$ as follows:

$$
54=a (3-2)(3-9)(3-12) 54=a (1cdot-6cdot-9)
$$

$$
54=a 54 a=1
$$

The polynomial equation that represent the data is,

$$
f(x)=(x-2)(x-9)(x-12)
$$

$$
text{color{#4257b2}(c) Is this trend likely to continue? What the domain of that function should be realistic.}
$$

Yes this trend of curve likely to continue, and the domain of this function is equal, $(0, infty)$

$$
text{color{Brown}(a) See the graph. (b) $f(x)=(x-2)(x-9)(x-12)$.
\ \
(c) Yes this trend of curve likely to continue, and the domain of this function is equal, $(0, infty)$.}
$$

Write the equation for the figure in text book.

$$
text{color{#4257b2} (a) First figure}
$$

The function is upward, so the leading function is positive.

The degree of function is $(3)$ cubic function.

The function cross $x$ axis at point [-2, -1, 1]

$$
f(x)=a(x+2)(x+1)(x-1)
$$

Use point $(0, -2)$ to get the value of $a$ as follows:

$$
-2=a(0+2)(0+1)(0-1) -2=a(2cdot1cdot-1)
$$

$$
-2=acdot-2 a=dfrac{-2}{-2} a=1
$$

$$
f(x)=(x+2)(x+1)(x-1)
$$

$$
text{color{#4257b2} (b) Second figure}
$$

The function is downward, so the leading function is negative.

The degree of function is $(3)$ cubic function.

The function cross $x$ axis at point [-4, -2, 1]

$$
f(x)=-a(x+4)(x+2)(x-1)
$$

Use point $(-31, -1.6)$ to get the value of $a$ as follows:

$$
-1.6=-a(-3+4)(-3+2)(-3-1) -1.6=-a(1cdot-1cdot-4)
$$

$$
-1.6=-acdot4 a=dfrac{-1.6}{-4} a=0.4
$$

$$
f(x)=-0.4 (x+4)(x+2)(x-1)
$$

$$
text{color{Brown}(a) $f(x)=(x+2)(x+1)(x-1)$
\ \
(b) $f(x)=-0.4 (x+4)(x+2)(x-1)$}
$$

(a) Determine the quadratic function that has zeros [-3, -5] and $f(7)=-720$

Quadratic function standard form is $f(x)=a (x-x_{1})(x-x_{2})$

$$
f(x)=a (x+3)(x+5)
$$

$$
f(7)=a (7+3)(7+5)=-720 -720=a(10cdot12)
$$

$$
-720=120a a=-dfrac{720}{120} a=-6
$$

$$
f(x)=a (x-x_{1})(x-x_{2})
$$

$$
f(x)=-6(x+3)(x+5)
$$

(a) Determine the cubic function that has zeros [-2, 3, 4] and $f(5)=28$

Quadratic function standard form is $f(x)=a (x-x_{1})(x-x_{2})(x-x_{3})$

$$
f(x)=a (x+2)(x-3)(x-4)
$$

$$
f(5)=a (5+2)(5-3)(5-4)=28 28=a(7cdot2cdot1)
$$

$$
28=14a a=dfrac{28}{14} a=2
$$

$$
f(x)=a (x-x_{1})(x-x_{2})(x-x_{3})
$$

$$
f(x)=2(x+2)(x-3)(x-4)
$$

$$
text{color{Brown}(a) $f(x)=-6(x+3)(x+5)$
\ \
(b) $f(x)=2(x+2)(x-3)(x-4)$}
$$

Determine the value of $k$ for the function $y=kx^3-8x^2-x+3k+1$ if has a zero at $x=2$

Substitute the value of $x=2$ as follows:

$$
0=8k-32-2+3k+1 11k=33
$$

$$
k=dfrac{33}{11} k=3
$$

$$
y=3x^3-8x^2-x+10
$$

$$
y=(x+1)(x-2)(3x-5)
$$

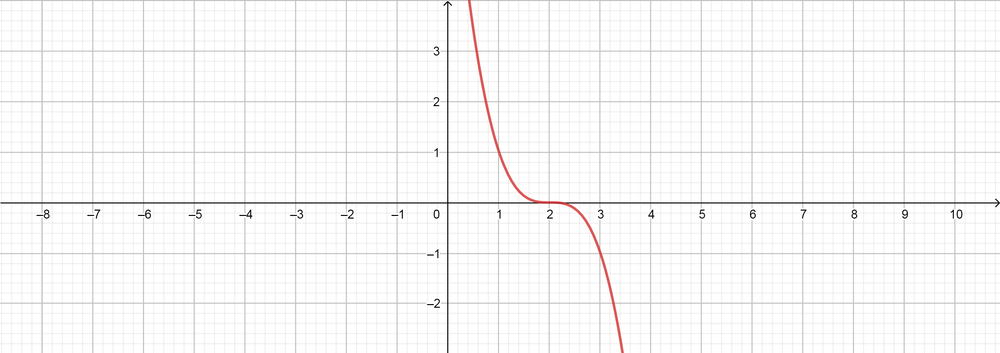
$$
text{color{Brown}$k=3$
\ \
$y=3x^3-8x^2-x+10$
\ \
$y=(x+1)(x-2)(3x-5)$}
$$

Describe what you know about each of the following graph.

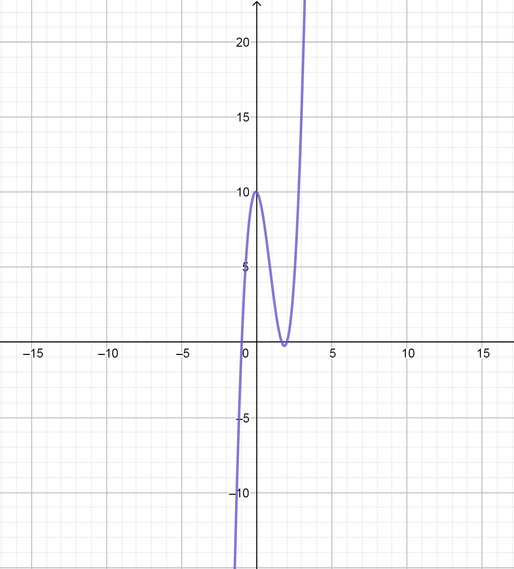
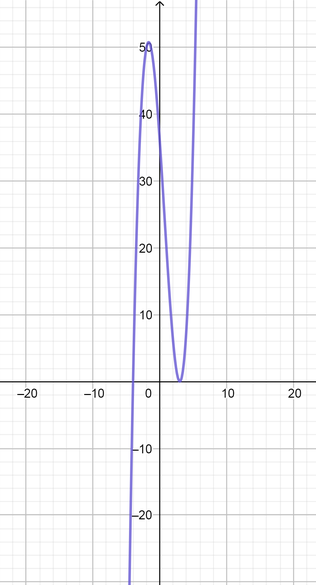
(a) $y=a(x-2)^2(x-4)^2$

From graph we know that:

The function intersect with $x$ axis at points $x=2, x=4$

The function is a quartic function because it has a degree of $(n=4)$

The function is upward, because the leading coefficient is positive

The function has the same end behavior , because the degree is even number

The function may have turning point about $[3, 1]$

The function may have a $[0, 1, 2, 3, 4]$ zeros

(b) $y=a(x-2)^2(x-4)^2$

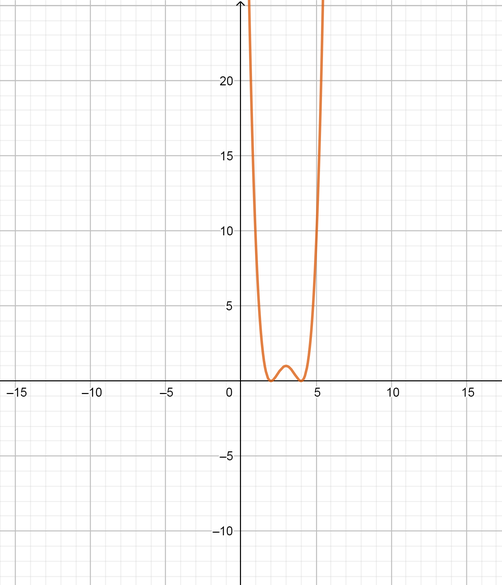
From graph we know that:

The function intersect with $x$ axis at points $x=3, x=-4$

The function is a cubic function because it has a degree of $(n=3)$

The function is upward, because the leading coefficient is positive

The function has opposite end behavior , because the degree is odd number

The function may have turning point about $[2, 0]$

The function may have a $[0, 1, 2, 3]$ zeros

$$
text{color{Brown}(a) The function intersect with $x$ axis at points $x=2, x=4$
\ \
The function is a quartic function because it has a degree of $(n=4)$
\ \
(b) The function intersect with $x$ axis at points $x=3, x=-4$
\ \
The function is a cubic function because it has a degree of $(n=3)$}
$$

A square corner cut from a $(30)$ cm by $(20)$cm cardboard to create a box. Volume of new box represented by, $V(x)=x(30-2x)(20-2x)$, where $(x)$ is the height, answer for the following question.

$$
text{color{#4257b2}(a) Calculate the volume of the box with height of $(2)$ cm}
$$

$$
V(x)=x(30-2x)(20-2x)
$$

Substitute the value of $(x=2)$ as follows:

$$
V(x)=2cdot (30-2(2))cdot (20-2(2)) V(x)=2cdot26cdot16
$$

$$
V(x)=832 text{cm}^3
$$

$$
text{color{#4257b2}(b) Calculate the dimensions of the box with a volume of $(1000)$ cm$^3$}
$$

$$
V(x)=x(30-2x)(20-2x)
$$

Use distributive property as follows:

$$
1000=x[600-60x-40x+4x^2] V(x)=4x^3-100x^2+600x=1000
$$

$$
{V}'(x)=12x^2-200x+600=0
$$

Divide the entire equation by $(4)$ as follows:

$$
3x^2-50x+150=0
$$

Use discriminant property for quadratic equation $left[x=dfrac{-bpmsqrt{b^2-4ac}}{2a}right]$ as follows:

$$
a=3 b=-50 c=150
$$

$$
x=dfrac{50pmsqrt{(50)^2-(4cdot3cdot150)}}{2cdot3} x=dfrac{50pmsqrt{2500-1800}}{6}
$$

$$
x=dfrac{50+sqrt{700}}{6} x=12.74
$$

$$
x=dfrac{50-sqrt{700}}{6} x=3.92
$$

$$
V(x)=x(30-2x)(20-2x)
$$

Use zero property to find the range value of $(x)$ as follows:

$$
30-2xge0 -2xge-30 xle15
$$

$$
20-2xge0 -2xge-20 xle10
$$

According these ranges values of $(x)$, the matched value of $(x)$ is equal, $(3.92)$

The dimensions of box are:

Height, $=3.92$ cm

Length, $=30-2(3.92)=22.16$ cm

Width, $=20-2(3.92)=12.16$ cm

$$
text{color{#4257b2}(c) Solve $V(x)>0$ and discuss the meaning of your solution.}
$$

$$
V(x)=x(30-2x)(20-2x)
$$

Use zero property to find the range value of $(x)$ as follows:

$$
30-2x>0 -2x>-30 x0 -2x>-20 x<10
$$

The dimensions of $(x)$ should be less than $(10)$ to be correct and satisfied.

$$
text{color{#4257b2}(d) State the restriction in the context of question.}
$$

To create a square corner box from $(30)$ cm by $(20)$ cm, you should cut square with dimension of $(3.92)$cm by $(3.92)$ cm from each corner.

$$
text{color{Brown}(a) $V(x)=832 text{cm}^3$
\ \
(b) Height $=3.92$ cm Length $=22.16$ cm Width $=12.16$ cm
\ \
(c) The dimensions of $(x)$ should be less than $(10)$ to be correct and satisfied.
\ \
(d) To create a square corner box from $(30)$ cm by $(20)$ cm, you should cut square with dimension of $(3.92)$cm by $(3.92)$ cm from each corner.}
$$