State the degree, leading coefficient and end behavior for the following expression.

$$
color{#4257b2}text{(a)} f(x)=-4x^4+3x^2-15x+5
$$

Degree is equal $4$ [Higher degree]

Leading coefficient is equal $-4$

Degree is even number, so the the end behavior is the same.

$$
color{#4257b2}text{(b)} g(x)=2x^5-4x^3+10x^2-13x+8
$$

Degree is equal $5$ [Higher degree]

Leading coefficient is equal $2$

Degree is odd number, so the the end behavior is opposite.

$$
color{#4257b2}text{(c)} p(x)=4-5x+4x^2-3x^3
$$

Degree is equal $3$ [Higher degree]

Leading coefficient is equal $-3$

Degree is odd number, so the the end behavior is opposite.

$$
color{#4257b2}text{(d)} h(x)=2x(x-5)(3x+2)(4x-3)
$$

Use distributive property as follows:

$$
(2x^2-10x)(12x^2-9x+8x-6)
$$

$$
24x^4-18x^3+16x^3-12x^2-120x^3+90x^2-80x^2+60x
$$

Add similar tiles to group like terms as follows:

$$
24x^4+(-18x^3+16x^3-120x^3)+(-12x^2+90x^2-80x^2)+60x
$$

$$
24x^4-122x^3-2×62+60x
$$

Degree is equal $4$ [Higher degree]

Leading coefficient is equal $24$

Degree is even number, so the the end behavior is the same

(a) Degree$=4$ Leading coefficient $=-4$ End behavior the same

(b) Degree$=5$ Leading coefficient $=2$ End behavior is opposite

(c) Degree$=3$ Leading coefficient $=-3$ End behavior is opposite

(d) Degree$=4$ Leading coefficient $=24$ End behavior the same

Determine the minimum and maximum number of turning point for each function in Ex.1

$$
color{#4257b2}text{(a)} f(x)=-4x^4+3x^2-15x+5
$$

Degree is even number equal $4$, so:

Turn point may have $[3, 1]$

Number of zeros may have $[0, 1, 2, 3, 4]$

$$
color{#4257b2}text{(b)} g(x)=2x^5-4x^3+10x^2-13x+8
$$

Degree is even number equal $5$, so:

Turn point may have $[4, 2, 0]$

Number of zeros may have $[1, 2, 3, 4, 5]$

$$
color{#4257b2}text{(c)} p(x)=4-5x+4x^2-3x^3
$$

Degree is even number equal $3$, so:

Turn point may have $[2, 0]$

Number of zeros may have $[1, 2, 3]$

$$
color{#4257b2}text{(d)} h(x)=24x^4-122x^3-2×62+60x
$$

Degree is even number equal $4$, so:

Turn point may have $[3, 1]$

Number of zeros may have $[0, 1, 2, 3, 4]$

$$
text{color{Brown}(a) Turn point may have $[3, 1]$ Number of zeros may have $[0, 1, 2, 3, 4]$
\ \
(b) Turn point may have $[4, 2, 0]$ Number of zeros may have $[1, 2, 3, 4, 5]$
\ \
(c) Turn point may have $[2, 0]$ Number of zeros may have $[1, 2, 3]$
\ \
(d) Turn point may have $[3, 1]$ Number of zeros may have $[0, 1, 2, 3, 4]$}
$$

Answer for the following question.

$$
color{#4257b2}text{(a) The function has an even or odd degree. }
$$

(I) Degree number is even $4$ (II) Degree number is even $6$

(III) Degree number is odd $5$ (IV) Degree number is even $2$

(V) Degree number is odd $3$ (IV) Degree number is odd $3$

$$
color{#4257b2}text{(b) The leading coefficient is positive or negative.}
$$

(I) Leading coefficient is negative (II) Leading coefficient is negative

(III) Leading coefficient is negative (IV) Leading coefficient is positive

(V) Leading coefficient is negative (IV) Leading coefficient is positive

$$
color{#4257b2}(a)
$$

(I) Degree number is even $4$ (II) Degree number is even $6$

(III) Degree number is odd $5$ (IV) Degree number is even $2$

(V) Degree number is odd $3$ (IV) Degree number is odd $3$

$$
color{#4257b2}text{(b)}
$$

(I) Leading coefficient is negative (II) Leading coefficient is negative

(III) Leading coefficient is negative (IV) Leading coefficient is positive

(V) Leading coefficient is negative (IV) Leading coefficient is positive

Use the degree of the following equations to describe the end behavior.

$$
color{#4257b2}text{(a)} f(x)=2x^2-3x+5
$$

Degree of the function is even $2$, so the end behavior is the same

$$
color{#4257b2}text{(b)} f(x)=-3x^3+2x^2+5x+1
$$

Degree of the function is odd $3$, so the end behavior is opposite

$$
color{#4257b2}text{(c)} f(x)=5x^3-2x^2-2x+6
$$

Degree of the function is odd $3$, so the end behavior is opposite

$$
color{#4257b2}text{(d)} f(x)=-2x^4+5x^3-2x^2+3x-1
$$

Degree of the function is even $4$, so the end behavior is the same

$$
color{#4257b2}text{(e)} f(x)=0.5x^4+2x^2-6
$$

Degree of the function is even $4$, so the end behavior is the same

$$
color{#4257b2}text{(f)} f(x)=-3x^5+2x^3-4x
$$

Degree of the function is odd $5$, so the end behavior is opposite

$$
text{color{Brown}(a) Degree of the function is even $2$, so the end behavior is the same
\ \
(b) Degree of the function is odd $3$, so the end behavior is opposite
\ \
(c) Degree of the function is odd $3$, so the end behavior is opposite
\ \
(d) Degree of the function is even $4$, so the end behavior is the same
\ \
(e) Degree of the function is even $4$, so the end behavior is the same
\ \
(f) Degree of the function is odd $5$, so the end behavior is opposite}
$$

Match the following functions with matched figure.

$$
color{#4257b2}text{(a)} y=2x^3-4x^2+3x+2
$$

Figure (B)

$$
color{#4257b2}text{(b)} y=x^4-x^3-4x^2-5x
$$

Figure (A)

$$
color{#4257b2}text{(a)} y=-4x^4+3x^2+4
$$

Figure (E)

$$
color{#4257b2}text{(a)} y=-2x^5+3x^4+6x^3-10×62+2x+5
$$

Figure (C)

$$
color{#4257b2}text{(a)} y=x^2+3x-5
$$

Figure (F)

$$
color{#4257b2}text{(a)} y=3x^3+5x^2-3x+1
$$

Figure (D)

$$
text{color{Brown}$text{(a) Figure (B)}$ $text{(b) Figure (A)}$
\ \
$text{(c) Figure (E)}$ $text{(d) Figure (C)}$
\ \
$text{(e) Figure (F)}$ $text{(f) Figure (D)}$}
$$

Give an example for the following end behavior

$$
color{#4257b2}text{(a) As} (xrightarrow-infty, yrightarrow-infty) text{and as }(xrightarrowinfty, yrightarrowinfty)
$$

The leading coefficient has a positive value as follows:

$$
3x^3+5x^2-3x+1
$$

$$
color{#4257b2}text{(b) As} (xrightarrowpminfty) text{and as }(yrightarrowinfty)
$$

The leading coefficient has a positive value as follows:

$$
x^2+3x-5
$$

$$
color{#4257b2}text{(c) As} (xrightarrowpminfty) text{and as }(yrightarrow-infty)
$$

The leading coefficient has a negative value as follows:

$$
-3x^3+4x^2-5x+4
$$

$$
color{#4257b2}text{(d) As} (xrightarrow-infty, yrightarrowinfty) text{and as }(xrightarrowinfty, yrightarrow-infty)
$$

The leading coefficient has a negative value

$$
-x^2
$$

$$
text{color{Brown}(a) $3x^3+5x^2-3x+1$ (b) $x^2+3x-5$
\ \
(c) $-3x^3+4x^2-5x+4$ (d) $-x^2$}
$$

Sketch a graph of the polynomial function that represent the following condition.

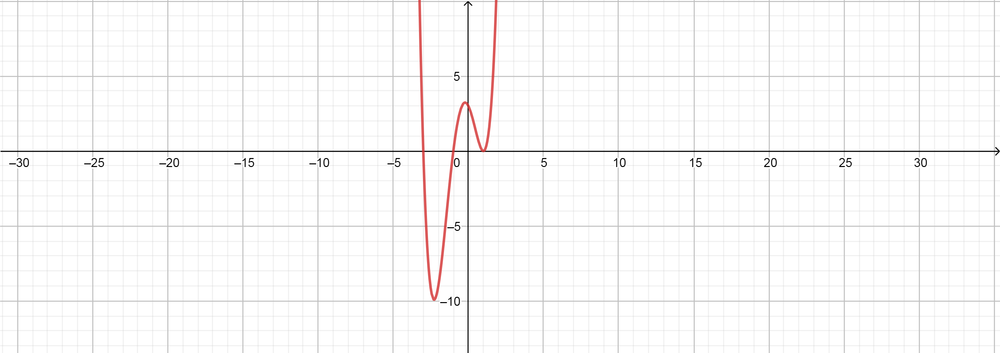
$$
text{color{#4257b2}[a] $(4)$ Degree, positive leading coefficient, $(3)$ zeros, $(3)$ turning points.}
$$

$$
f(x)=(x-1)^2(x+1)(x+3)
$$

$$
text{color{#4257b2}[b] $(4)$ Degree, negative leading coefficient, $(2)$ zeros, $(1)$ turning points.}
$$

$$
f(x)=-(x^2-1)(x^2+1)
$$

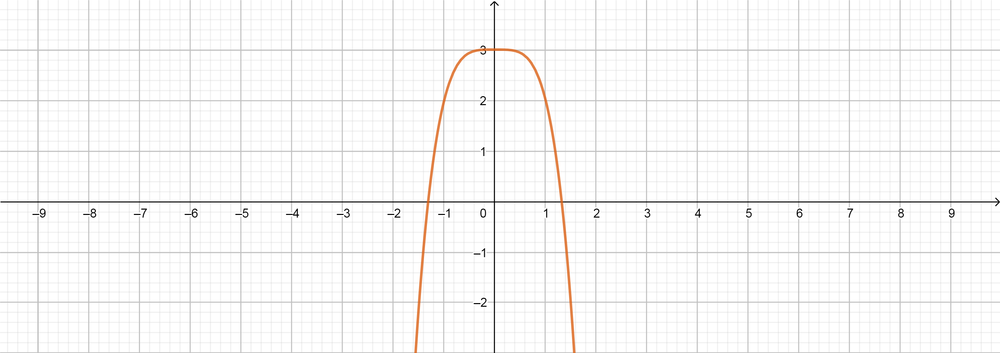
$$
text{color{#4257b2}[c] $(4)$ Degree, positive leading coefficient, $(1)$ zeros, $(3)$ turning points.}
$$

$$
f(x)=-dfrac{1}{2} x^4-dfrac{7}{2} x^3-7x^2-2x-dfrac{15}{100}
$$

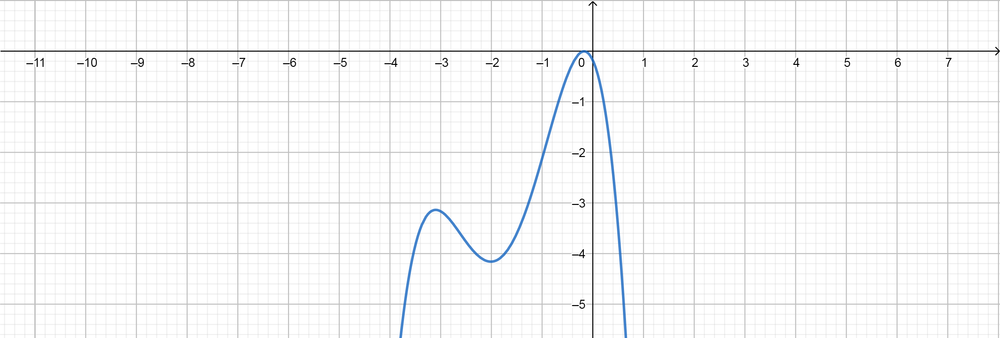
$$
text{color{#4257b2}[d] $(3)$ Degree, negative leading coefficient, $(1)$ zeros, no turning points.}
$$

$$
f(x)=-(x-2)^3
$$

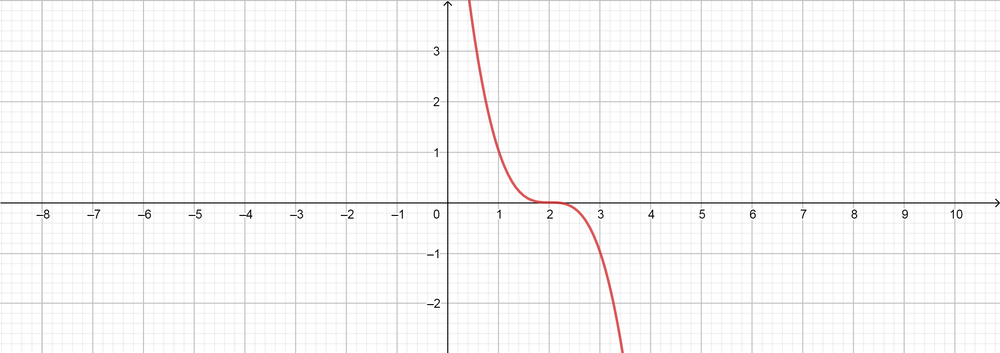
$$
text{color{#4257b2}[e] $(3)$ Degree, positive leading coefficient, $(2)$ zeros, $(2)$ turning points.}
$$

$$
f(x)=x(x-2)^2
$$

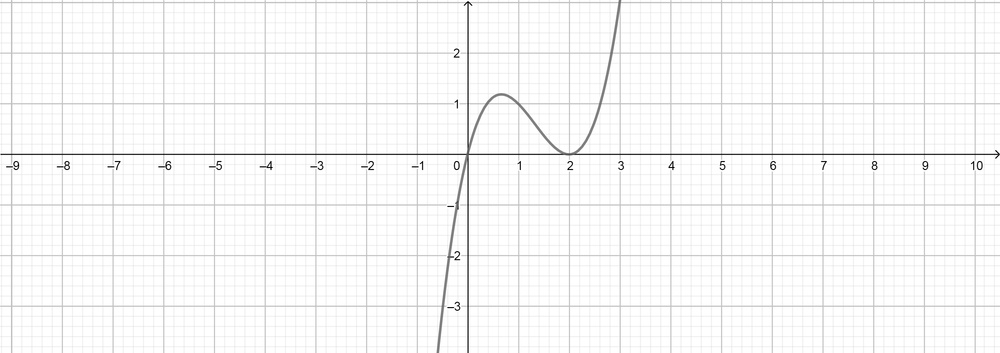
$$
text{color{#4257b2}[f] $(4)$ Degree, positive leading coefficient, $(2)$ zeros, $(3)$ turning points.}
$$

$$
f(x)=(x-1)^2(x+1)^2
$$

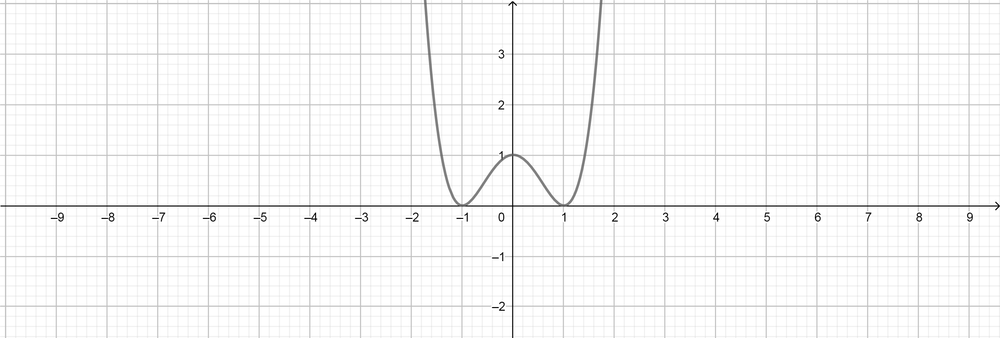
$$
text{color{Brown}See graphs}
$$

Explain why odd functional can have only local minimums and maximums but the even functional can have only absolute minimums and maximums.

$lozenge$ For even functional:

This is confirmed by the end behaviors because they are the same.

$lozenge$ For odd functional:

The end behaviors are opposite, so they have local minimums and maximums.

$$
text{color{Brown}For even functional: This is confirmed by the end behaviors because they are the same.
\ \ \
For odd functional: The end behaviors are opposite, so they have a local minimums and maximums}
$$

$$
text{color{#4257b2}The graph of the function of $f(x)=ax^b-cx$ is symmetrical with respect to the origin and that it has some turning points. That the graph has an odd or even turning points}
$$

$because$ The graph is symmetric with origin $therefore f(-x)=-f(x)$

$$
f(-x)=-ax^b+cx -f(x)=-ax^b+cx
$$

The function of the graph is an odd function, so the turning points for odd function should be an even number.

The graph of function of $f(x)=ax^b-cx$ has an even turning points.

$$
text{color{Brown}The graph of function of $f(x)=ax^b-cx$ has an even turning points}
$$

Sketch a graph for a cubic function with following terms.

{$text{color{#4257b2}(a) Only one point intersect with $x$ axis
\
$$x^3+8$$}$

{$text{color{#4257b2}(a) Two points intersect with $x$ axis
\
$$x^3-4x^2$$}$

{$text{color{#4257b2}(a) Three points intersect with $x$ axis
\
$$x^3+2x^2-5x-6$$}$

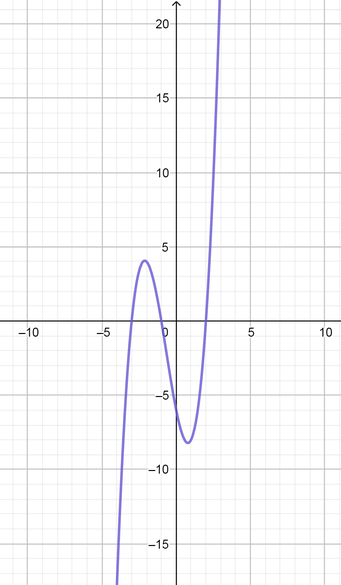
$$
text{color{Brown}See sketches}
$$

Sketch a graph for a quartic function with following terms.

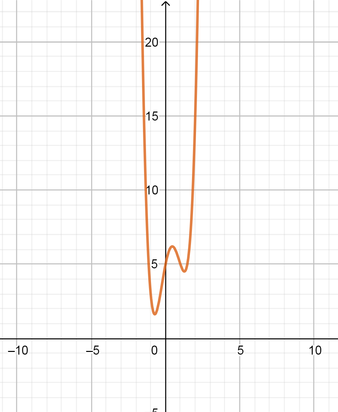
{$text{color{#4257b2}(a) No point intersect with $x$ axis
\
$$3x^4-4x^3-4x^2+5x+5$$}$

Sketch a graph for a cubic function with following terms.

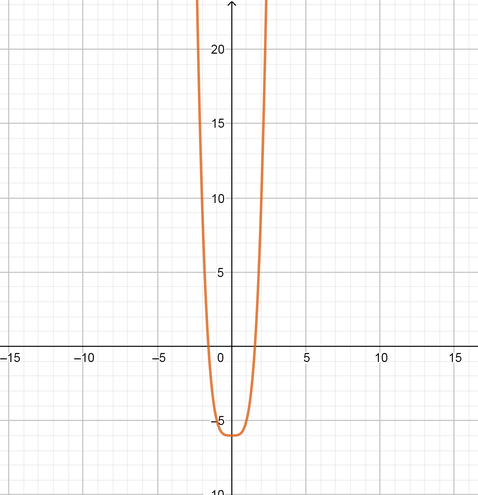
{$text{color{#4257b2}(b) Tow points intersect with $x$ axis
\
$$x^4-5$$}$

Sketch a graph for a cubic function with following terms.

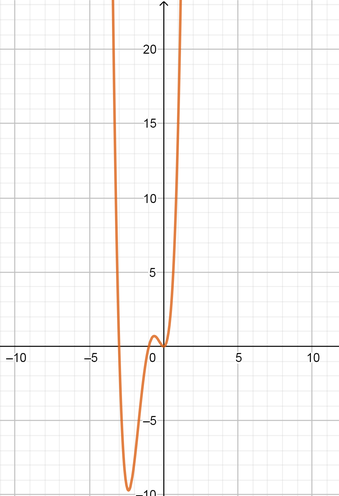
{$text{color{#4257b2}(c) Three points intersect with $x$ axis
\
$$2x^4+8x^3+6x^2$$}$

Sketch a graph for a cubic function with following terms.

{$text{color{#4257b2}(d) Four points intersect with $x$ axis
\
$$-x^4-2x^3+x^2+2x$$}$

{$text{color{#4257b2}(e) One point intersect with $x$ axis
\
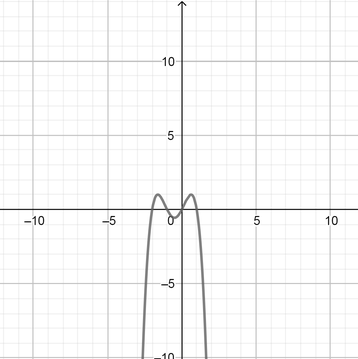
$$x^4$$}$

$$
text{color{Brown}See sketches}
$$

The degree of a polynomial function has to be at least one more than the number of turning points. Since we are given a total of three turning points, our polynomial will be at least fourth degree, hence in some form of
$$
f(x)=ax^4+bx^3+cx^2+dc+e$$

Note that the given turning points are $x=-2$, $x=0$ and $x=3$. These are the points at which the graph of a function changes the behavior from decreasing to increasing and vice versa. These numbers for any $x$ satisfy the condition
$$
begin{align*}
(x-(-2))(x-0)(x-3)&=0&&text{[Simplify]}\
(x+2)x(x-3)&=0&&text{[Multiply]}\
x^3-x^2-6x&=0
end{align*}$$

Now raising the power of each term by $1$ and dividing the each termby the power of $x$, we obtain
$$
dfrac{x^4}{4}-dfrac{x^3}{3}-6dfrac{x^2}{2}=f(x).
$$
Hence,
$$
f(x)=dfrac{1}{4}x^4-dfrac{1}{3}x^3-3x^2.tag{1}
$$
and this function has the turning points $x=-2$, $x=0$, $x=3$.

We can alter the function $(1)$ by adding the constant term, or multiplying or dividing each term by the same number, and the turning points will remain the same.

The same turning points will have a function with any added constant term to $(1)$, such as
$$
begin{align*}
f(x)&=dfrac{1}{4}x^4-dfrac{1}{3}x^3-3x^2+5\
f(x)&=dfrac{1}{4}x^4-dfrac{1}{3}x^3-3x^2-2.
end{align*}$$

The same turning points will have a function if we multiply each term of function $(1)$ by the same number and add any constant term, such as
$$
begin{align*}
f(x)&=x^4-dfrac{4}{3}x^3-12x^2+1&&text{[Multiplied by $4$]}\
f(x)&=dfrac{3}{4}x^4-x^3-9x^2-2.&&text{[Multiplied by $3$]}\
end{align*}$$

The same turning points will have a function if we divide each term of function $(1)$ by the same number and add any constant term, such as
$$
begin{align*}
f(x)&=dfrac{1}{8}x^4-dfrac{1}{6}x^3-dfrac{3}{2}x^2+2&&text{[Divided by $2$]}\
f(x)&=dfrac{1}{12}x^4-dfrac{1}{9}x^3-x^2-1.&&text{[Divided by $3$]}
end{align*}$$

*(a)* We can choose any two functions from the previous step or any other function obtained by adding the constant term, or multiplying or dividing each term of the function $(1)$ by the same number.
We will choose
$$
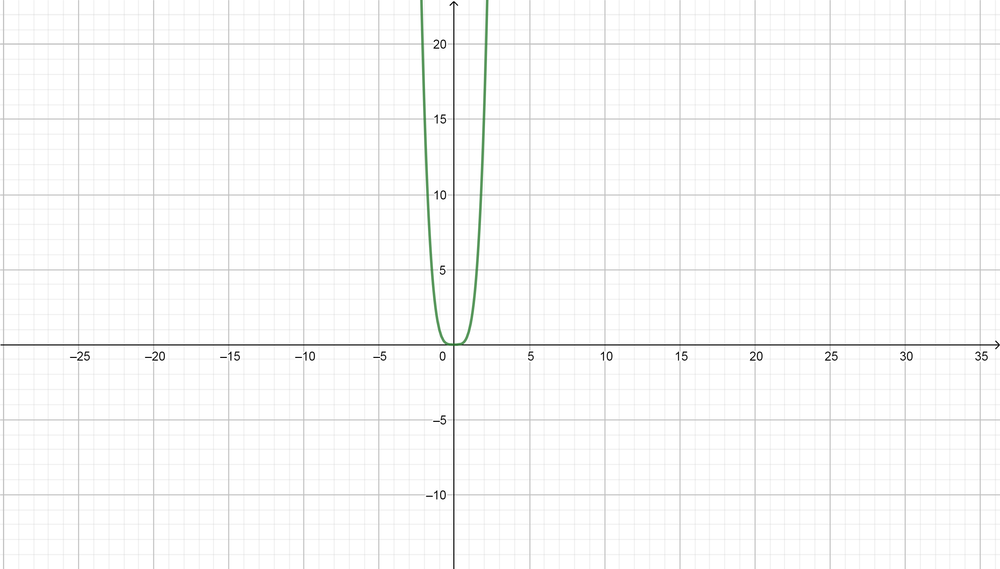
y=x^4-dfrac{4}{3}x^3-12x^2+1 text{and} y=dfrac{1}{12}x^4-dfrac{1}{9}x^3-x^2-1
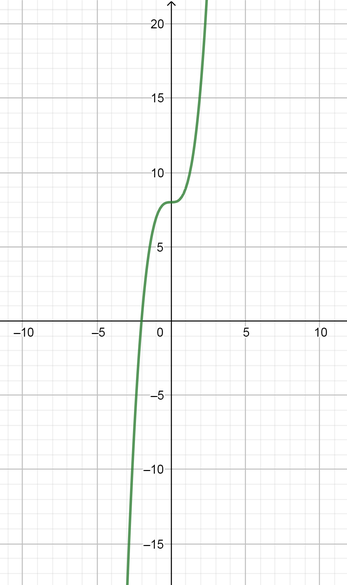
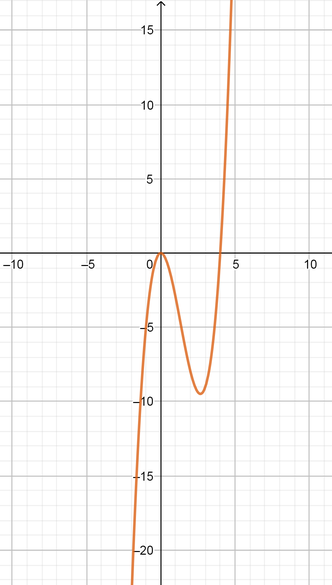
$$
Graph the two functions in *Figure 1*.

*Figure 1.* The graph of the two functions

*(b)* Note that these functions have different $y$ intercepts as well different zero values ( $x$ intercepts). Hence, if we need to sketch the graph of only one such function, an additional condition could be the $y$ intercepts by adding a specific constant term. For the first function the $y$ intercept is $1$, and for the second one $-1$.

(a) What was the population of the town in $1900$?

Note that the population expressed by $y=-0.1x^4+0.5x^3+0.4x^2+10x+7$

Population since $1900$, that mean $x=0$

$$
y=-0.1(0)^4+0.5(0)^3+0.4(0)^2+10(0)+7
$$

$$
y=0+7 y=7
$$

The population is $y=7$ in hundred

(b) Describe what happen of the population over time.

Note that, if the number of year since $1900$ is increase, the population in hundred is increase too.

$$
text{color{Brown}(a) $y=7$ in hundred.
\ \
(b) The population in hundred is increase.}
$$

Decide whether each of the following terms is true or false.

(a) $f$ Is an even function $text{color{#4257b2}True}$

(b) $f$ Can not be an odd function $text{color{#4257b2}True}$

(c) $f$ Will have at least one zero $text{color{#4257b2}False}$

(d) $f$ As $xrightarrowpminfty$ and $yrightarrowinfty$ $text{color{#4257b2}True}$

$$
text{color{Brown}(a) True (b) True (c) False (d) True}
$$

$$
text{color{Brown}(I) What is the degree of the equation?
\ \
(II) What is the sign of the leading coefficient?
\ \
(III) What is the end behavior of the equation?}
$$

(a) What must be true about the function if an even function?

$$
color{#4257b2}y=ax^2+bx+c
$$

This function may have no zeros

This function may have a turning point $n-1$

This function have the same end behavior

(b) What must be true about the function if an odd function?

$$
color{#4257b2}y=ax^3+bx^2+cx+d
$$

This function must have at least one zeros

This function may have a turning point $n-1$

This function have the opposite end behavior

$$
text{color{Brown}(a) This function may have no zeros
\ \
This function may have a turning point $n-1$
\ \
This function has the same end behavior.
\ \
(b) This function must have at least one zeros
\ \
This function may have a turning point $n-1$
\ \
This function has the opposite end behavior.}
$$