#### (b)

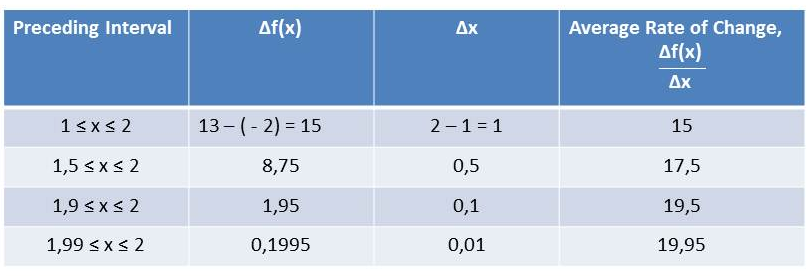
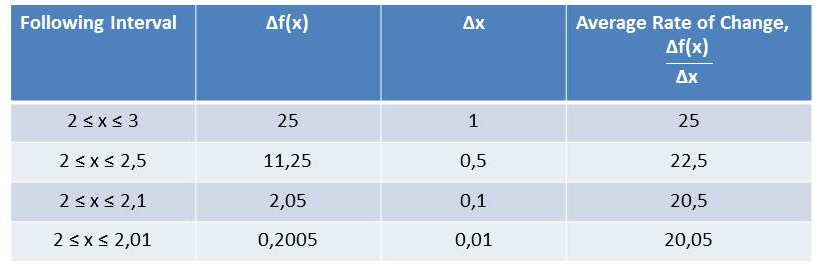
Here, we will use intervals $1.99leq{x}leq2$ and $2leq{x}leq2.01$ because, they are the smallest intervals on either side of $x=2$ so, according to previous explanation on pages $80$ and $81$, we have $textbf{the instantaneous rate of change when}$ $x=2$ is:

$dfrac{19.95+20.05}{2}=dfrac{40}{2}=20$

#### (a)

Here, using the preceding and following interval method, according to earlier explanations, we have next:

First, let’s find average rate of change on interval $1.5leq{t}leq2$:

$dfrac{Delta{f(t)}}{Delta{t}}=dfrac{30.9-26.98}{2-1.5}=dfrac{3.92}{0.5}=7.84$

Now, let’s find average rate of change on interval $2leq{t}leq2.5$:

$dfrac{Delta{f(t)}}{Delta{t}}=dfrac{32.3830.9}{2.5-2}=dfrac{1.48}{0.5}=2.96$

And finally, $textbf{the instantaneous rate of change in the height of the ball at exactly }$ $t=2$ is:

$$
dfrac{7.84+2.96}{2}=5.4
$$

#### (b)

Here, using the centred interval method, we will use interval $1.5leq{t}leq2.5$, because it is the smallest of given intervals which contains $t=2$, and we have that $textbf{ the instantaneous rate of change in the height of the ball at exactly }$ $t=2$ is:

$dfrac{32.38-26.98}{2.5-1.5}=5.4$

#### (c)

I prefer $textbf{the centred interval method}$ because it easier and simplier to calculate $textbf{the instantaneous rate of change}$.

#### (a)

$textbf{The population of raccoons at $2.5$ months will be:}$

$P(2.5)=100+30cdot2.5+4cdot2.5^2=200$

#### (b)

$textbf{The average rate of change in the raccoon population
over the interval}$ $0leq{t}leq2.5$ will be:

$textbf{average rate of change}$ = $dfrac{P(2.5)-P(0)}{2.5-0}=dfrac{200-100}{2.5}=40$

#### (c)

$textbf{The rate of change in the raccoon population at exactly
$2.5$ months is}$:

$dfrac{P(2.51)-P(2.49)}{2.51-2.49}=dfrac{100.5004-99.9004}{0.02}=30$

#### (d)

Answers for parts (a), (b), and (c) are different because at each part we calculated different things.At part (a) it was total population at $t=2.5$, at part (b) it was the average number by which the population has changed from moment $t=0$ to moment $t=2.5$, and at pasrt (c) we calculated change in the number at exactly $t=2.5$.

#### (a)

Here, we will use interval $-2.01leq{x}leq-1.99$ to estimate the $textbf{instantaneous rate of change}$ at $x=-2$:

$$
begin{align*}
textbf{instantaneous rate of change} &= dfrac{6cdot(-1.99)^2-4-(6cdot(-2.01)^2-4)}{-1.99+2.01}\
&=dfrac{23.7606-24.2406}{0.02}\
&=-24\
end{align*}
$$

#### (b)

Here, we will use interval $-0.01leq{x}leq0.01$ to estimate the $textbf{instantaneous rate of change}$ at $x=0$:

$$
begin{align*}
textbf{instantaneous rate of change} &= dfrac{6cdot(-0.01)^2-4-(6cdot(0.01)^2-4)}{0.01+0.01}\
&=dfrac{0}{0.02}\
&=0\
end{align*}
$$

#### (c)

Here, we will use interval $3.99leq{x}leq4.01$ to estimate the $textbf{instantaneous rate of change}$ at $x=4$:

$$
begin{align*}
textbf{instantaneous rate of change} &= dfrac{6cdot4.01^2-4-(6cdot3.99^2-4)}{4.01-3.99}\
&=dfrac{96.4806-95.5206}{0.02}\
&=48\
end{align*}
$$

#### (d)

Here, we will use interval $7.99leq{x}leq8.01$ to estimate the $textbf{instantaneous rate of change}$ at $x=8$:

$$
begin{align*}
textbf{instantaneous rate of change} &= dfrac{6cdot8.01^2-4-(6cdot7.99^2-4)}{8.01-7.99}\
&=dfrac{384.9606-383.0406}{0.02}\
&=96\
end{align*}
$$

We will use interval $2.99leq{x}leq3.01$, and we will have that $textbf{the
instantaneous rate of change in the object’s height at}$ $x=3 s$ is:

$$
begin{align*}
textbf{the instantaneous rate of change}&=dfrac{-5cdot3.01^2+3cdot3.01+65-(-5cdot2.99^2+3cdot2.99+65)}{3.01-2.99}=\
&=dfrac{-36.2705+35.7305}{0.02}\
&=-27\
end{align*}
$$

Here, we will use interval $7.99leq{x}leq8.01$ to estimate the
instantaneous rate of change in the home’s value at the start of the
eighth year of owning the home, and we have next:

$textbf{instantaneous rate of change}$=$$dfrac{125000(1.06)^{8.01}-125000(1.06)^{7.99}}{8.01-7.99}$=11608.974
$$
\
$$

11608.974$

#### (a)

Here our interval is $2000leq{t}leq2024$, and the average rate of change in the population is:

$textbf{average rate of change}$ = $dfrac{P(2024)-P(2000)}{2024-2000}=-6000$

#### (b)

It means that number of people is getting smaller, in average, for $6000$ ther ewill be less people from $2000$ to $2024$.

#### (c)

First, we have $textbf{average rate of change}$ from $2000$ to $2012$:

$textbf{average rate of change}$ = $dfrac{P(2012)-P(2000)}{2012-2000}=-5982$

Now, we have $textbf{average rate of change}$ from $2012$ to $2012$:

$textbf{average rate of change}$ = $dfrac{P(2024)-P(2012)}{2024-2012}=-6018$

To prove part (b), we have that average rate of change in the population from $2000$ to $2024$, including results from this part is really $6000$:

$textbf{average rate of change}$ = $dfrac{-5982-6018}{2}=-6000$

#### (d)

$textbf{The instantaneous rate of change in the population }$ will be $0$ for $t=2000$.

Let’s take interval $4.99leq{x}leq5.01$ to estimate $textbf{the instantaneous
rate of change}$ in the value of the car when the car is $5$ years old:

$textbf{the instantaneous rate of change}$ = $dfrac{V(5.01)-V(4.99)}{5.01-4.99}=-959.5$

It means that the price of the car at the moment $t=5$ years is for $959.5
$$
lower.\
$$

-959.5$

#### (a)

The time when the diver will enter the water, $t$, we will find $textbf{solving following quadriatic equation}$:

$0=10+2t-4.9t^2$

Here, the height above the water, function $h(t)$, is $0$ at the moment when the diver enters the water. And, solving this quadriatic equation, we get that $textbf{diver will enter the water for}$ $t=1.65 s$.

#### (b)

Here, we will estimate the rate at which the diver’s height above the water is changing as the diver enters the waterm using following formula for speed, $v$.

$v=dfrac{s}{t}=dfrac{10}{1.65}=6.06$ m/s

Here, $s$ is $10m$, that is height of the diver above the water, and $t$ is the time we found in part (a), $textbf{so the solution is}$ $6.06$ m/s.

First, we will use $textbf{preceding and following interval method.}$We will calculate average rate of change on interval $4.99leq{r}leq5$:

$textbf{average rate of change}$=$dfrac{V(5)-V(4.99)}{5-4.99}=100$

Now, we will calculate it on interval $5leq{r}leq5.01$:

$textbf{average rate of change}$=$dfrac{V(5.01)-V(5)}{5.01-5}=100$

Now, we will estimate $textbf{the instantaneous rate of change}$ in the volume of the snowbal for $r=5$:

$textbf{the instantaneous rate of change}$=$dfrac{100+100}{2}=100$

The second method will be $textbf{the centered interval method}$, we will use interval $4.99leq{r}leq5.01$:

$textbf{the instantaneous rate of change}$=$dfrac{V(5.01)-V(4.99)}{5.01-4.99}=100$

The actual movement of the body along some of the paths with which the speed changes can be divided into a number of stages. At each stage, the body passes a certain path for a certain time interval. The total passage is obtained by gathering the crossed roads at all stages. The total travel time is obtained by collecting all time intervals. $textbf{The average speed is the ratio of the total traveled path and the total time interval. The informations he must know are: current traffic situation, meteorological conditions, current state of the road}$.

#### (a)

Here, we will use $textbf{centred interval method}$, we will take interval $3leq{t}leq5$, for $t=4$ min, so we have that $textbf{the instantaneous rate of change in the temperature of the oven at exactly}$ $t=4$ is:

$$
dfrac{Delta{T}}{Delta{t}}=dfrac{305-350}{5-3}=-22.5^circ F/min
$$

#### (b)

Using quadratic regression, $textbf{an equation which represent the data}$,
rounding to two decimal places, is the model:

$f(t)=-1.96t^2-9.82t+400.71$,

where $f(t)$ is oven temperature and $t$ is time.

Now, we will calculate the average rate of change in oven temperature using a very small centred interval near $t=4$, let’s take interval $3.99leq{t}leq4.01$. The instaneous rate of change in temperature at $5$ min is:

$dfrac{Delta{f(t)}}{Delta{t}}=dfrac{f(4.01)-f(3.99)}{4.01-3.99}=-104^circ F/min$

#### (c)

$textbf{Our answers are different because we used different intervals}$.

#### (d)

$textbf{The better estimate is at part (b)}$ because we used much smaller interval, so, and estimate is much better.

#### (a)

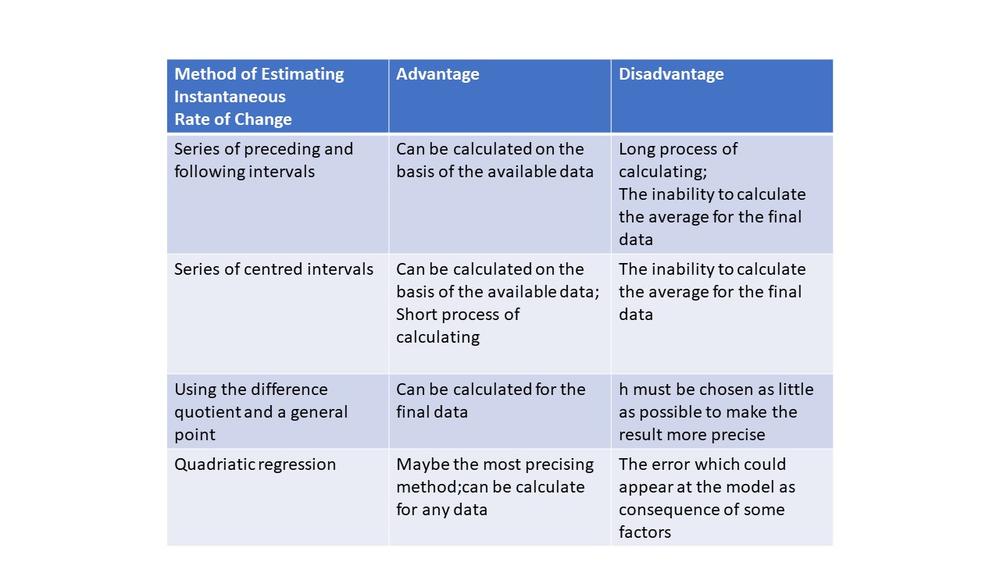
Let’s first calculate area of the circle for $r_1=0$ cm:

$P_1=r_1^2pi=0^2pi=0 cm^2$

Now, we will find area of the circle for $r_2=100$ cm:

$P_2=r_2^2pi=100^2pi=10000pi cm^2$

Next, we will find $textbf{average rate of change in the area for one circle}$:

$textbf{average rate of change}$ = $dfrac{P_2-P_1}{r_2-r_1}=dfrac{10000pi-0}{100-0}=100pi$

#### (b)

Let’s first calculate area of the circle for $r_1=119.99$ cm:

$P_1=r_1^2pi=119.99^2pi=14376.01 cm^2$

Now, we will find area of the circle for $r_2=120.01$ cm:

$P_2=r_2^2pi=120.01^2pi=14402.4001pi cm^2$

Now, we will find $textbf{instaneous rate of change in the area}$, in order to find how fast is the area changing when the radius is $r=120$ cm:

$dfrac{Delta{P}}{Delta{r}}=dfrac{P_2-P_1}{r_2-r_1}=1319.505pi$

(a) $100pi$; (b) $1319.505pi$

First, we will find area of a crystal in the shape of a cube for the side length of the crystal is $a_1=2.99$ cm:

$P_1=6a_1^2=6cdot{2.99^2}=53.6406cm^2$

Now, we will find area of a crystal in the shape of a cube for the side length of the crystal is $a_2=3.01$ cm:

$P_2=6a_2^2=6cdot{3.01^2}=54.3606cm^2$

Finally, we will $textbf{estimate instaneous rate of change}$ at which the surface area is changing when the side length of the crystal is $r=3$ cm:

$dfrac{Delta{P}}{Delta{a}}=dfrac{54.3606-53.6406}{3.01-2.99}=36$

Fist, we will find area of a spherical balloon when its radius is $r_1=19.99$ cm:

$P_1=4r_1^2pi=4cdot{19.99^2}pi=1598.4004 cm^2$

Now, we will find area of a spherical balloon when its radius is $r_2=20.01$ cm:

$P_2=4r_2^2pi=4cdot{20.01^2}pi=1601.6004 cm^2$

And finally, we will $textbf{estimate the instaneous rate at which its surface area is changing}$ when the radius is $r=20$ cm:

$dfrac{Delta{P}}{Delta{r}}=dfrac{P_2-P_1}{r_2-r_1}=160$