Solution of this task is based on graphs of functions in previous task.

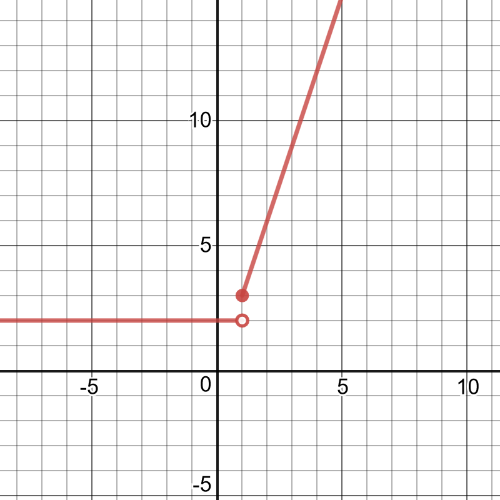
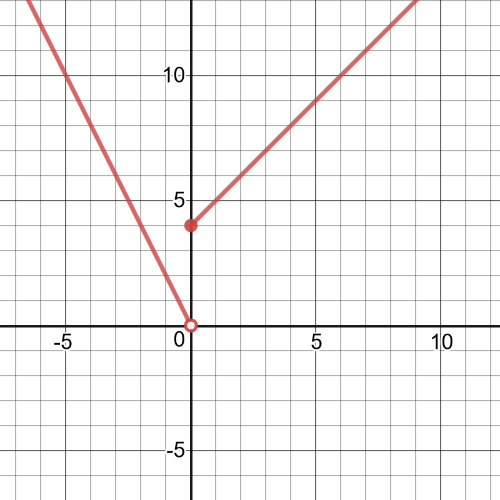
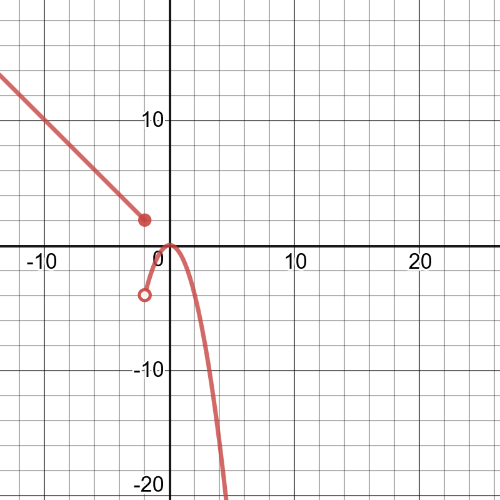
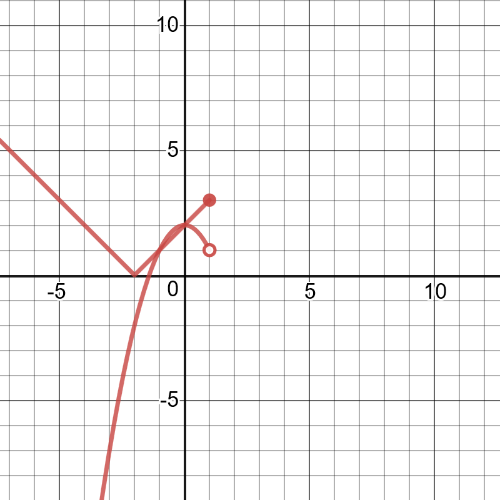
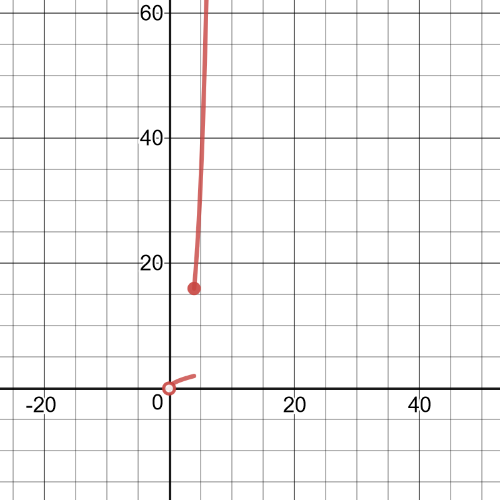
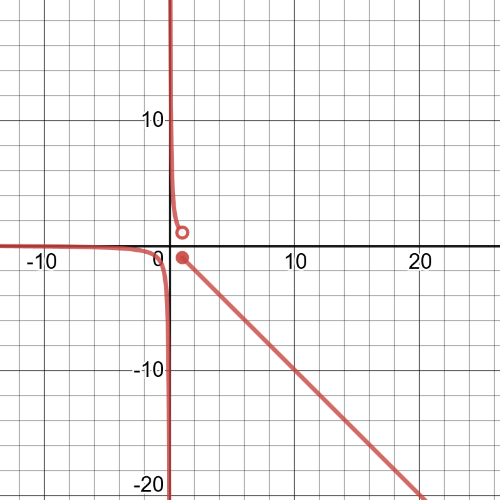
#### (a)

$f(x)$ $textbf{is discontinuous at}$ $x=1$

#### (b)

$f(x)$ $textbf{is discontinuous at}$ $x=0$

#### (c)

$f(x)$ $textbf{is discontinuous at}$ $x=-2$

#### (d)

$f(x)$ $textbf{is discontinuous at}$ $x=1$

#### (e)

$f(x)$ $textbf{is discontinuous at}$ $x=0$

#### (f)

$f(x)$ $textbf{is discontinuous at}$ $x=1$

The solution of this task are following functions:

#### (a)

$$
f(x)=begin{cases}
x^2-2 &, xleq1\
x+1 &, x>1\
end{cases}
$$

#### (b)

$$
f(x)=begin{cases}
left|x+1 right| &, x<1\
sqrt{x}+1 &, xgeq1\
end{cases}
$$

#### (a)

$$
f(x)=begin{cases}
x^2-2 &, xleq1\
x+1 &, x>1\
end{cases}
$$

#### (b)

$$
f(x)=begin{cases}
left|x+1 right| &, x<1\
sqrt{x}+1 &, xgeq1\
end{cases}
$$

#### (a)

$textbf{The domain}$ of this function is $D=Bbb{R}$.

This function is $textbf{discontinuous}$ because all the pieces of
the function not join together at the endpoints of the given intervals.

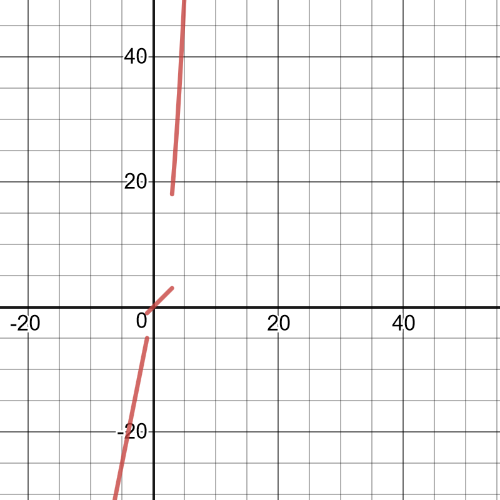
#### (b)

$textbf{The domain}$ of this function is $D=Bbb{R}$.

This function is $textbf{continuous}$ because all the pieces of
the function join together at the endpoints of the given intervals.

#### (a)

This function is $textbf{discontionuous}$ because all the pieces of
the function not join together at the endpoints of the given intervals.

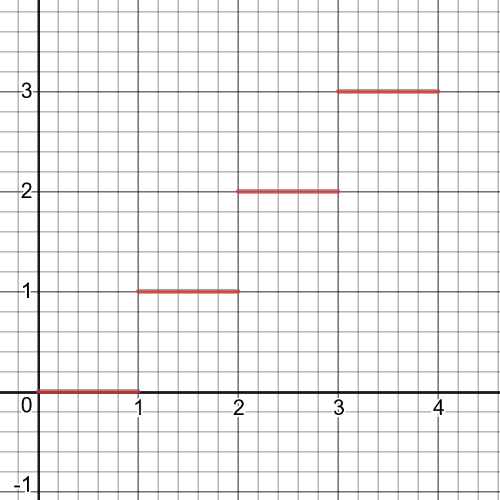
$textbf{The domain}$ of this function is $D=Bbb{R}$ and $textbf{the range}$ is $R=left{2,3 right}$.

$textbf{The graph}$ of this function is on the following picture:

#### (b)

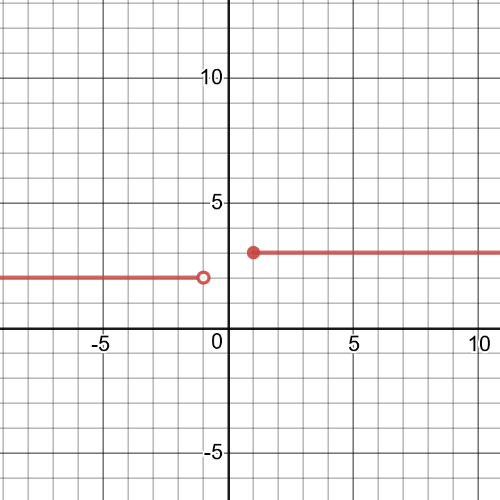
This function is $textbf{contionuous}$ because all the pieces of
the function join together at the endpoints of the given intervals.

$textbf{The domain}$ of this function is $D=Bbb{R}$ and $textbf{the range}$ is $R=left[0,infty right)$.

$textbf{The graph}$ of this function is on the following picture:

#### (c)

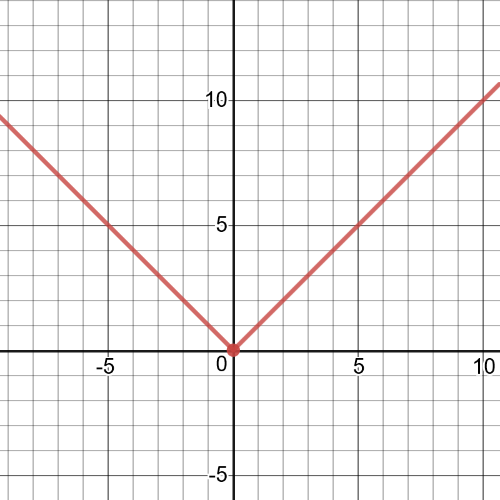
This function is $textbf{contionuous}$ because all the pieces of
the function join together at the endpoints of the given intervals.

$textbf{The domain}$ of this function is $D=Bbb{R}$ and $textbf{the range}$ is $R=left[1,infty right)$.

$textbf{The graph}$ of this function is on the following picture:

#### (b)

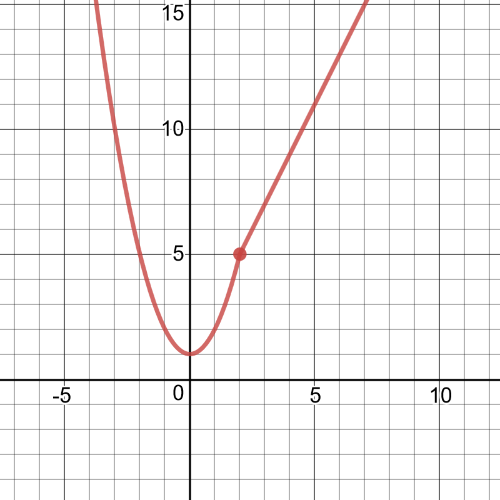
This function is $textbf{contionuous}$ because all the pieces of
the function join together at the endpoints of the given intervals.

$textbf{The domain}$ of this function is $D=Bbb{R}$ and $textbf{the range}$ is $R=left[1,5 right]$.

$textbf{The graph}$ of this function is on the following picture:

A function that describes
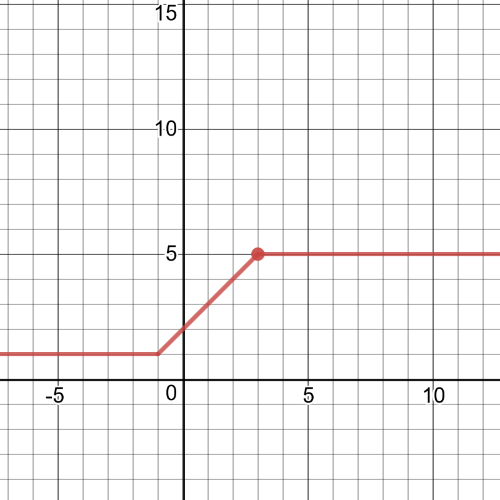
Graham’s total long-distance charge in terms of the number of long
distance minutes he uses in a month is:

$$
f(x)=begin{cases}
15 &, xleq500\
0.02&, x>500\
end{cases}
$$

A piecewise function that models this situation is:

$$
f(x)=begin{cases}
0.35x &, 0leq{x}leq100000\
0.45x-10000 &, 100000500000\
end{cases}
$$

$$
f(x)=begin{cases}
0.35x &, 0leq{x}leq100000\
0.45x-10000 &, 100000500000\
end{cases}
$$

$textbf{The value of $k$}$ for which is the following function continuous is for $k=4$.

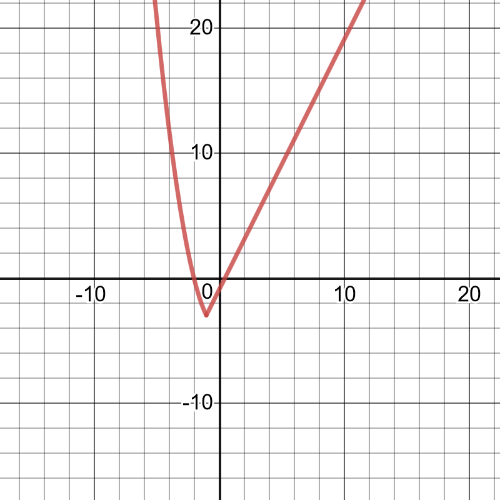
Here we have $textbf{the graph}$ of this function, for $k=4$:

#### (a)

Here we have $textbf{the graph}$ of this function:

#### (b)

This function is $textbf{discontinuous}$ at $x=6$.

#### (c)

We will calculate $2^x-(4x+8)$ at $x=6$.

$2^6-(4cdot6+8)=64-32=32$ fishes.
#### (d)

Using the function that represents the time after the spill

$4x+8=64$

$4x=56$

$x=14$

#### (e)

For example: $3$ possible events are environmental chages, introduction of a new predator and increased fishing.

$$
f(x)=begin{cases}
x+3 &, xgeq-3\
-(x+3) &, x<-3\
end{cases}
$$

And,here is the graph which follows this function:

This function is $textbf{continuous}$,because all the pieces of
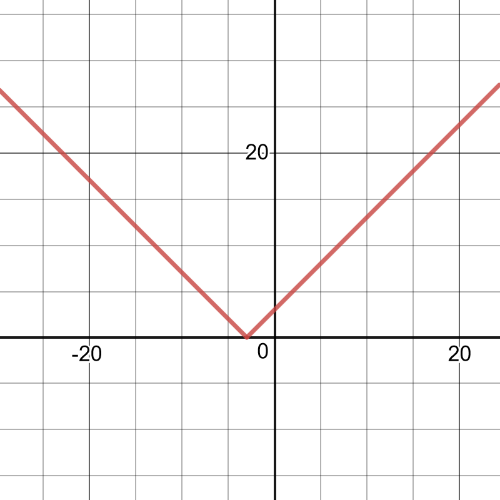
the function join together at the endpoints of the given intervals.We can see that from the following graph of this function:

$textbf{This piecewise function}$ is actually the following function:

$$
f(x)=begin{cases}
0 &, 0leq{x}<10\
10 &, 10leq{x}<20\
20 &, 20leq{x}<30\
30 &, 30leq{x}<40\
40 &, 40leq{x}<50\
end{cases}
$$

And, $textbf{the graph}$ of this function is on the following picture:

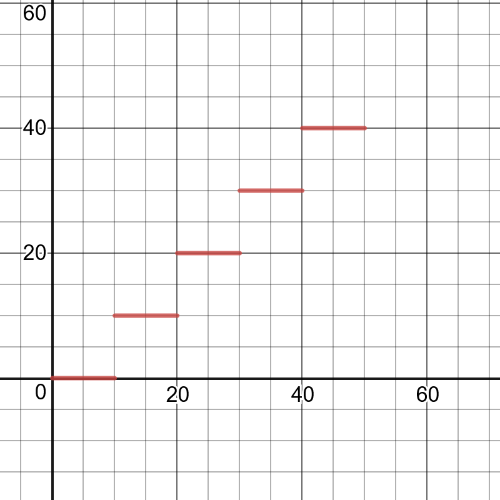
$$
f(x)=begin{cases}
0 &, 0leq{x}<10\
10 &, 10leq{x}<20\
20 &, 20leq{x}<30\
30 &, 30leq{x}<40\
40 &, 40leq{x}<50\
end{cases}
$$

Adding or subtracting factors to the function $y = x$ makes this function for the value of $k$ move up or down by $y$-axis. The graph shows that even for one function $y = x$ can not be simultaneously connected to the functions $y=5x$ and $y=2x^2$ , so it can not be continuous for one $k$.

$textbf{The graph}$ of this function is on the following picture:

#### (a)

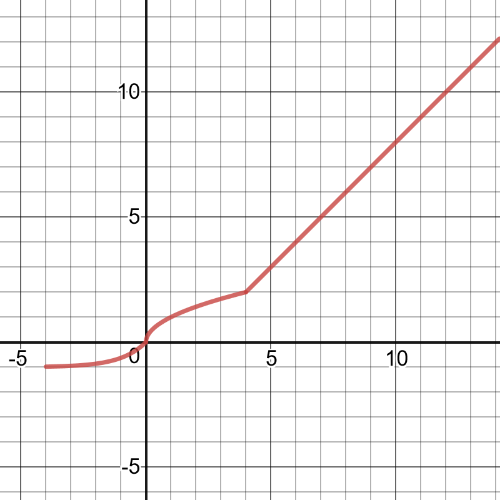
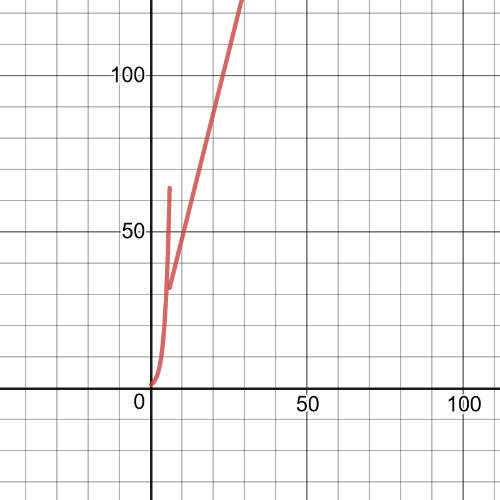
For example, for this task we can use $textbf{following function}$ which is made of three parent functions, $y=e^x$, $y=sqrt{x}$ and $y=x$.

$$
f(x)=begin{cases}
e^x &, -4leq{x}<0\
sqrt{x} &, 0leq{x}<4\
x &, {x}geq4\
end{cases}
$$

#### (b)

Here we have $textbf{the graph}$ of the function we created at $(a)$:

#### (c)

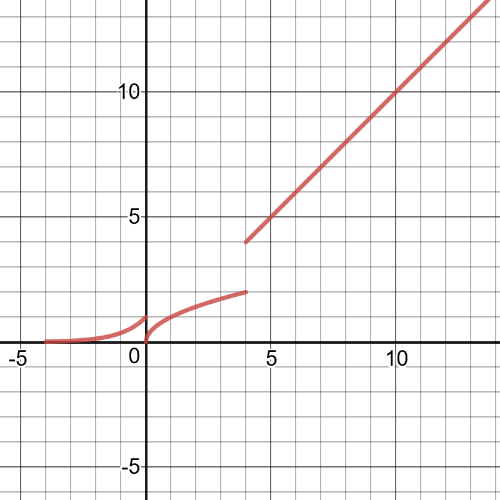
This function is $textbf{discontinuous}$ because all the pieces of
the function not join together at the endpoints of the given intervals.We can see that from previous graph of this function.

#### (d)

We can transform function we made at $(a)$ in the following function and by this transformation we will make continious function:

$$
f(x)=begin{cases}
e^x-1 &, -4leq{x}<0\
sqrt{x} &, 0leq{x}<4\
x-2 &, {x}geq4\
end{cases}
$$

We can see and from the following graph of this transformed function that it is $textbf{continuous}$: