#### (a)

Domain is $textbf{R}$ and the range is

$$
begin{equation*}
left[-2,-4 right]
end{equation*}
$$

This relation is a function according to vertical line test.
#### (b)

The domain is

$$
begin{equation*}
left[-1,+infty right]
end{equation*}
$$

and the range is

$$
begin{equation*}
left[1,+infty right]
end{equation*}
$$

This is a function according to vertical line test
#### (c)

The domain is

$$
begin{equation*}
left{1,2,3,4 right}
end{equation*}
$$

the range is

$$
begin{equation*}
left{-5,4,7,9,11 right}
end{equation*}
$$

This is not a function according to diagram.Actually,1 is mapped into more than one element, in 4 and 9.
#### (d)

The domain and the range is $textbf{R}$ and this is the function because from creating the table of values we can see that each point is mapped to exactly one point.
#### (e)

The domain is

$$
begin{equation*}
left{-4,-3,1,2 right}
end{equation*}
$$

the range is

$$
begin{equation*}
left{-0,1,2,3 right}
end{equation*}
$$

And this is function, we can see that from diagram.

#### (f)

The domain is $textbf{R}$ and the range is

$$
begin{equation*}
left(-infty,0 right]
end{equation*}
$$

and this is the function, we can conclude that making a table of value.

#### (a)

Domain: $textbf{R}$,
Range:

$$
begin{equation*}
left[-2,-4 right]
end{equation*}
$$

It is the function
#### (b)

Domain:

$$
begin{equation*}
left[-1,+infty right]
end{equation*}
$$

Range:

$$
begin{equation*}
left[1,+infty right]
end{equation*}
$$

#### (c)

Domain:

$$
begin{equation*}
left{1,2,3,4 right}
end{equation*}
$$

Range:

$$
begin{equation*}
left{-5,4,7,9,11 right}
end{equation*}
$$

It is not function.
#### (d)

Domain and range are $textbf{R}$ and it is the function.
#### (e)

Domain:

$$
begin{equation*}
left{-4,-3,1,2 right}
end{equation*}
$$

Range:

$$
begin{equation*}
left{0,1,2,3 right}
end{equation*}
$$

It is the function
#### (f)

Domain is $textbf{R}$, range is

$$
begin{equation*}
left(-infty,0 right]
end{equation*}
$$

It is the function

#### (a)

Domain and the range is $textbf{R}$
This relation is a function, we can see that by creating the table of values.
#### (b)

The domain is $textbf{R}$ without -3 and the range is $textbf{R}$
This is a function according to table of values.
#### (c)

The domain is $textbf{R}$, the range is

$$
begin{equation*}
left(0,1 right]
end{equation*}
$$

We can check that this is the function by vertical line test.
#### (d)

The domain is $textbf{R}$ and the range is

$$
begin{equation*}
left[0,2 right]
end{equation*}
$$

Again, this is the function according to vertical line test.
#### (e)

The domain is

$$
begin{equation*}
left[-3,3 right]
end{equation*}
$$

the range is

$$
begin{equation*}
left[-3,3 right]
end{equation*}
$$

And this is function, we can see that apply vertical line test.
#### (f)

The domain is $textbf{R}$ and the range is

$$
begin{equation*}
left[-2,2 right]
end{equation*}
$$

and this is the function, we can check that by creating a table of values.

#### (a)

Domain and the range is $textbf{R}$
This relation is a function.
#### (b)

The domain is $textbf{R}$ without -3 and the range is $textbf{R}$
This is a function.
#### (c)

The domain is $textbf{R}$, the range is

$$
begin{equation*}
left(0,1 right]
end{equation*}
$$

|This is the function.
#### (d)

The domain is $textbf{R}$ and the range is

$$
begin{equation*}
left[0,2 right]
end{equation*}
$$

This is the function.
#### (e)

The domain is

$$
begin{equation*}
left[-3,3 right]
end{equation*}
$$

the range is

$$
begin{equation*}
left[-3,3 right]
end{equation*}
$$

This is function.
#### (f)

The domain is $textbf{R}$ and the range is

$$
begin{equation*}
left[-2,2 right]
end{equation*}
$$

This is the function

#### (a)

Domain is

$$
begin{equation*}
left{1,3,5,7 right}
end{equation*}
$$

The range is

$$
begin{equation*}
left{2,4,6 right}
end{equation*}
$$

This is the function.
#### (b)

The domain is

$$
begin{equation*}
left{0,1,2,5right}
end{equation*}
$$

The range is

$$
begin{equation*}
left{-1,3,6right}
end{equation*}
$$

This is a function.
#### (c)

The domain is

$$
begin{equation*}
left{0,1,2,3 right}
end{equation*}
$$

The range is

$$
begin{equation*}
left{2,4 right}
end{equation*}
$$

This is the function.
#### (d)

The domain is

$$
begin{equation*}
left{2,6,8 right}
end{equation*}
$$

The range is

$$
begin{equation*}
left{1,3,5,7 right}
end{equation*}
$$

This is not the function.
#### (e)

The domain is

$$
begin{equation*}
left{1,10,100 right}
end{equation*}
$$

the range is

$$
begin{equation*}
left{0,1,2,3 right}
end{equation*}
$$

This is not function.

#### (a)

Domain is

$$
begin{equation*}
left{1,3,5,7 right}
end{equation*}
$$

The range is

$$
begin{equation*}
left{2,4,6 right}
end{equation*}
$$

This is the function.
#### (b)

The domain is

$$
begin{equation*}
left{0,1,2,5right}
end{equation*}
$$

The range is

$$
begin{equation*}
left{-1,3,6right}
end{equation*}
$$

This is a function.
#### (c)

The domain is

$$
begin{equation*}
left{0,1,2,3 right}
end{equation*}
$$

The range is

$$
begin{equation*}
left{2,4 right}
end{equation*}
$$

This is the function.
#### (d)

The domain is

$$
begin{equation*}
left{2,6,8 right}
end{equation*}
$$

The range is

$$
begin{equation*}
left{1,3,5,7 right}
end{equation*}
$$

This is not the function.
#### (e)

The domain is

$$
begin{equation*}
left{1,10,100 right}
end{equation*}
$$

the range is

$$
begin{equation*}
left{0,1,2,3 right}
end{equation*}
$$

This is not function.

#### (a)

$$
f colon left{1,3,5,7 right} to left{2,4,6 right}
$$

This is the function.
#### (b)

$$
f colon left{0,1,2,5 right} to left{-1,3,6 right}
$$

This is a function.
#### (c)

$$
f colon left{0,1,2,3 right} to left{2,4right}
$$

This is the function.
#### (d)

$$
f colon left{2,6,8 right} to left{1,3,5,7 right}
$$

This is not the function.
#### (e)

$$
f colon left{1,10,100 right} to left{0,1,2,3 right}
$$

This is not function.
#### (f)

$$
f colon left{1,2,3,4right} to left{1,2,3,4right}
$$

This is the function

#### (a)

Domain and range is $textbf{R}$ and it is the function.
#### (b)

It is not the function
#### (c)

We have that

$$
begin{equation*}
y=dfrac{x^2}{2}-1
end{equation*}
$$

And this is the function, where $x$ is dependent variable.
#### (d)

Here we have that

$$
begin{equation*}
y=pmsqrt{x}
end{equation*}
$$

and this is not the function.
#### (e)

The domain is $textbf{R}$ without 0, the range is $textbf{R}$ and it is the function.
#### (f)

The domain and the range is $textbf{R}$ and this is the function.

#### (a)

Domain and range is $textbf{R}$ and it is the function.
#### (b)

It is not the function
#### (c)

This is the function,.
#### (d)

This is not the function.
#### (e)

The domain is $textbf{R}$ without 0, the range is $textbf{R}$ and it is the function.
#### (f)

The domain and the range is $textbf{R}$ and this is the function.

#### (a)

Here we have that $x$=3-$y$, or $y$=3+$x$.
#### (b)

Here is $y$=5-2$x$
#### (c)

(2+$x$)3=$y$, or $y$=3$x$+6
#### (d)

$x$+$y$=5, or $y$=5-$x$

#### (a)

$y$=3+$x$.
#### (b)

$y$=5-2$x$
#### (c)

$y$=3$x$+6
#### (d)

$y$=5-$x$

#### (a)

From the text of the task we have information that the length of the closet, $l$, is twice the size of its width, which is $w$, and we conclude that it is

$$
l=2w
$$

#### (b)

We have that $f(l)=w+l$ and from the task $l=2w$, so we have that $w=dfrac{l}{2}$, and finally, the equation for $f(l)$ is:

$$
begin{equation*}
f(l)=w+l=dfrac{l}{2}+l=dfrac{3}{2}l
end{equation*}
$$

#### (d)

We have, all from task that the $w+l=12$ and $l=2w$, so, when we replace $l$ in the first equation, we get:

$w+2w=12$

$3w=12$

$w=4$ and we get $l=12-4=8$
#### (c)

Here we have graph of $f(l)=dfrac{3}{2}l$

#### (a)

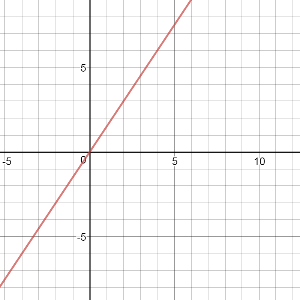
From the text of the task $l=2w$
#### (b)

$$
begin{equation*}
f(l)=w+l=dfrac{l}{2}+l=dfrac{3}{2}l
end{equation*}
$$

#### (c)

$w=4$, $l=8$

#### (b)

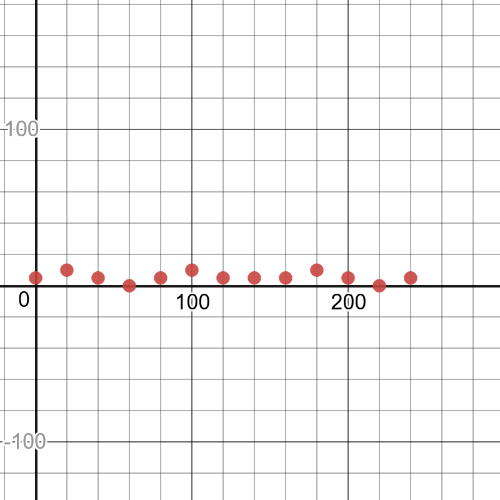
$$
D=left{0,20,40,60,80,100,120,140,160,180,200,220,240 right}
$$

#### (c)

$$
R=left{0,5,10 right}
$$

#### (d)

$textbf{It is a function}$ because it passes the vertical line test.
#### (e)

#### (f)

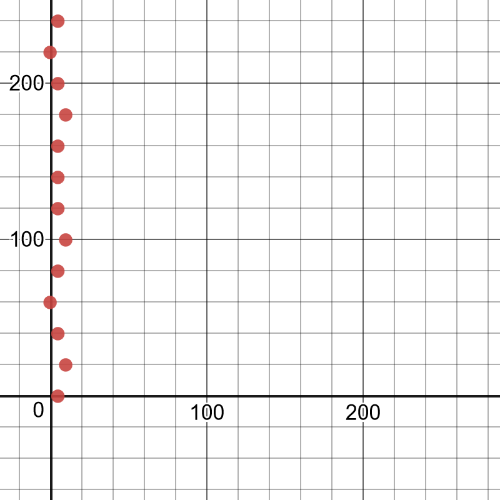
$textbf{It is not a function}$ because for example $(5,0)$ and $(5,40)$ are both in relation.

(b) $D=left{0,20,40,60,80,100,120,140,160,180,200,220,240 right}$;

(c) $R=left{0,5,10 right}$;

(d) $textbf{It is a function}$;

(f) $textbf{It is not a function}$

#### (a)

The next mapping is a function:

$$
begin{equation*}
left{left(1,3 right),left(2,2 right),left(3,1 right) right}
end{equation*}
$$

When we replace the coordinates we get a mapping which is still a function:

$$
begin{equation*}
left{left(3,1 right),left(2,2 right),left(1,3 right) right}
end{equation*}
$$

#### (b)

The next mapping is a function:

$$
begin{equation*}
left{left(1,1 right),left(2,1 right),left(3,2 right) right}
end{equation*}
$$

But when we replace the coordinates, we get a mapping that is no longer a function:

$$
begin{equation*}
left{left(1,1 right),left(1,2 right),left(2,3 right) right}
end{equation*}
$$

#### (c)

The next mapping is not a function:

$$
begin{equation*}
left{left(1,1 right),left(1,2 right) right}
end{equation*}
$$

When we replace the coordinates we get a mapping which is a function:

$$
begin{equation*}
left{left(1,1 right),left(2,1 right) right}
end{equation*}
$$

The relation that $textbf{fails the vertical test line}$ is not a function because it means there would be at least one point from the domain that would correspond at least two or more points from the codomains, depending on how many crosspoints there are with the graphics of the function and the vertical line that passes through that point from the domain .

#### (a)

$d=sqrt{(4-0)^2+(3-0)^2}=sqrt{4^2+3^2}=sqrt{25}=5$

$textbf{Yes}$, because the distance from $(4,3)$ to $(0,0)$ is $5$.
#### (b)

$d=sqrt{(1-0)^2+(5-0)^2}=sqrt{1^2+5^2}=sqrt{26}ne5$

$textbf{No}$, because the distance from $(1,5)$ to $(0,0)$ is not $5$.
#### (c)

$textbf{No}$, because $(4,3)$ and $(4,-3)$ are both in the relation.

#### (a)

Based on the values ​​for x and y from the table, we create the equation of the right through two points, that is, the required function.Let’s take $x_1=0, x_2=1, y_1=3, y_2=4$, so we have:

$y-y_1=dfrac{y_2-y_1}{x_2-x_1}(x-x_1)$

$y-4=dfrac{4-3}{1-0}(x-0)$

$$
y=x+4
$$

#### (b)

From the table, we have:

$g(3)-g(2)=12-7=5$

$g(3-2)=g(1)=4$

We get
$$
begin{equation*} 5ne4 end{equation*}
$$
so we conclude that

$$
begin{equation*} g(3)-g(2)ne{g(3-2)} end{equation*}
$$

#### (a)

$$
y=x+4
$$

#### (b)

$$
begin{equation*} g(3)-g(2)ne{g(3-2)}
end{equation*}
$$

#### (a)

The factors of 6 are 1, 2, 3 and 6.

$f(6)=1+2+3+6=12$

The factors of 7 are 1 and 7.

$f(7)=1+7=8$

The factors of 8 are 1, 2,4 and 8.

$f(8)=1+2+4+8=15$

#### (b)

The factors of 3 are 1 and 3.

$f(3)=1+3=4$

The factors of 5 are 1 and 5.

$f(5)=1+5=6$

The factors of 3 are 1 and 3.

$f(3)=1+3=4$

The factors of 15 are 1, 3, 5 and 15.

$f(15)=1+3+5+15=24$

And we have that:

$$
begin{equation*}
f(3)times{f(5)}=4times6=24
end{equation*}
$$

So, the coclusion is:

$$
begin{equation*}
f(3)times{f(5)}=f(15)
end{equation*}
$$

#### (c)

.The factors of 4 are 1, 2 and 4.

$f(4)=1+2+4=7$

The factors of 12 are 1, 2, 3 ,4, 6 and 12.

$f(12)=1+2+3+4+6+12=28$

And we have that:

$$
begin{equation*}
f(3)times{f(4)}=4times7=28
end{equation*}
$$

So, the coclusion is:

$$
begin{equation*}
f(3)times{f(4)}=f(12)
end{equation*}
$$

#### (c)

Yes, the sigma function of a number is a product of the sigma function of any two numbers contained in it, and which in the product give this number. In the general case, it is valid:

$$
begin{equation*}
{atimes{b}=c}Rightarrow{f(a)times{f(b)}=f(c)}
end{equation*}
$$

$color{#c34632}{x^2+y^2=25}$, this is not the function, we can see that from the graph of this function, applying test of vertical lines.The domain and the range of this relation is

$$
begin{equation*}
left[-5,5 right]
end{equation*}
$$

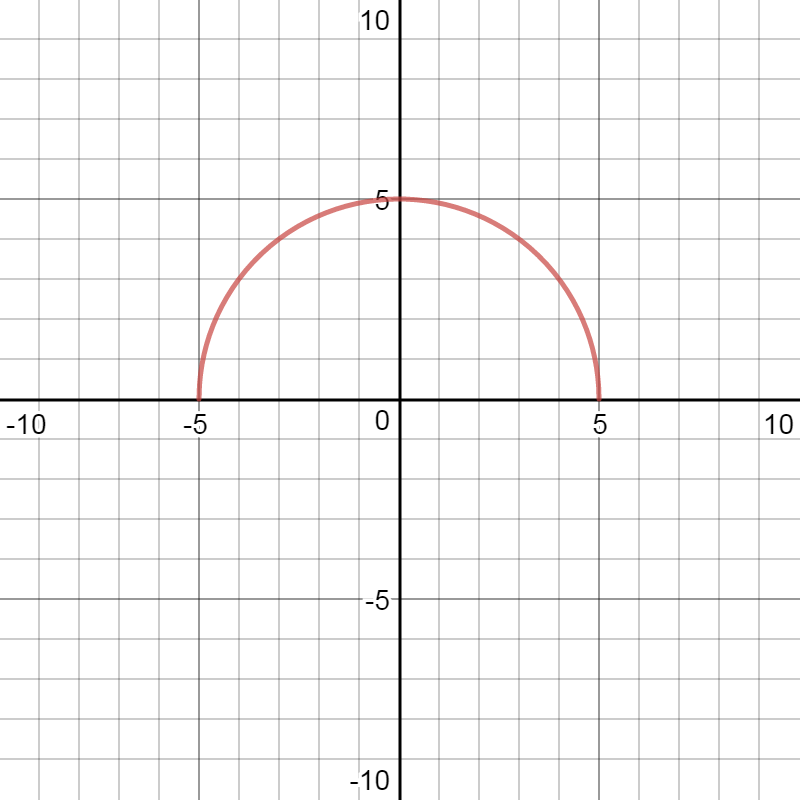
Here we have graph of this function:

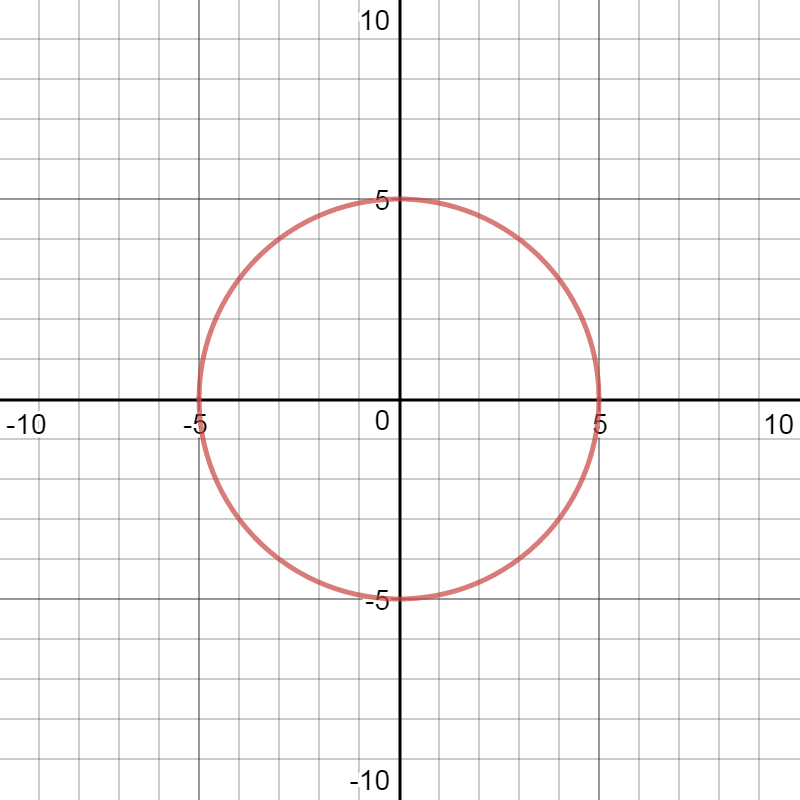
$$
begin{equation*}
textcolor{#c34632}{y=sqrt{25-x^2}}
end{equation*}
$$

This is the function, we can see that from the graph of this function, applying test of vertical lines.The domain of this function is

$$
begin{equation*}
left[-5,5 right]
end{equation*}
$$

and the range is

$$
begin{equation*}
left[0,5 right]
end{equation*}
$$

Here we have graph of this function:

Let $y$ be a function of $x$, that is, it involves the test of vertical lines.$x$ will be a function of $y$, if its domain is a codomain of $y$, and the codomain is the domain of the $y$ function, and of course, if the graph of $x$ passes the vertical line test.