If we have two points, for example, $A=left(x_1,y_1 right)$ and $B=left(x_2,y_2 right)$, $textbf{the slope of the line through those two points}$ would be:

$dfrac{y_2-y_1}{x_2-x_1}$

According to this, the solutions of our task are:

#### (a)

$textbf{The slope}$ through those two points, $A=left(2,3 right)=left(x_1.y_1 right)$ and $B=left(5,7 right)=left(x_2,y_2 right)$ is:

$dfrac{y_2-y_1}{x_2-x_1}=dfrac{7-3}{5-2}=dfrac{4}{3}$

#### (b)

$textbf{The slope}$ through those two points, $C=left(3,-1 right)=left(x_1.y_1 right)$ and $D=left(-4,5 right)=left(x_2,y_2 right)$ is:

$dfrac{y_2-y_1}{x_2-x_1}=dfrac{5+1}{-4-3}=dfrac{6}{-7}=-dfrac{6}{7}$

(a) $dfrac{4}{3}$; (b) $-dfrac{6}{7}$

We can pick any two points from the table and form function, for any two points,we will get the same function:

#### (a)

For example, we can pick points $left(1,1 right)=left(x_1,y_1 right)$ and $left(3,-5 right)=left(x_2,y_2 right)$ and of those function $textbf{we can form function}$ on the following way:

$y-y_1=dfrac{y_2-y_1}{x_2-x_1}left(x-x_1 right)$

$y-1=dfrac{-5-1}{3-1}left(x-1 right)$

$y=-dfrac{6}{2}left(x-1 right)+1$

$y=-3left(x-1 right)+1=-3x+3+1=-3x+4$

#### (b)

For example, we can pick points $left(1,0 right)=left(x_1,y_1 right)$ and $left(4,51 right)=left(x_2,y_2 right)$ and of those function $textbf{we can form function}$ on the following way:

$y-y_1=dfrac{y_2-y_1}{x_2-x_1}left(x-x_1 right)$

$y-0=dfrac{51-0}{4-1}left(x-1 right)$

$y=dfrac{50}{3}left(x-1 right)$

(a) $y=-3x+4$; (b) $y=dfrac{50}{3}left(x-1 right)$

#### (a)

$0=2x^2-x-6$

$0=(2x+3)(x-2)$

$0=2x+3$ and $0=x-2$

$0-3=2x+3-3$

$-3=2x$

$-dfrac{3}{2}=x$

$0+2=x-2+2$

$2=x$

$$
textbf{The zeros are $-dfrac{3}{2}$ and $2$.}
$$

#### (b)

$0=2^x-1$

$0+1=2^x-1+1$

$1=2^x$

$textbf{Any non-zero number raised to the exponent of $0$ is $1$,so $x=0$}$.

#### (c)

$0=sin(x-45^0), 0^0 leq x leq 360^0$

$sin(0^0), sin(180^0)$, and $sin(360^0)=0.$

$0^0=x-45^0, 180^0=x-45^0$, and $360^0=x-45^0$

$0^0+45^0=x-45^0+45^0$

$45^0=x$

$180^0+45^0=x-45^0+45^0$

$225^0=x$

$360^0+45^0=x-45^0+45^0$

$405^0=x$

$textbf{Because $0^0 leq x leq 360^0$,$ 405^0$ cannot be a zero.The zeros are $45^0$ and $225^0$}$

#### (d)

$0=2cos(x)$

$0=cos(x)$

For $-360^0 leq x leq 0^0, cos(-90^0)=0$ and $cos(-270^0)=0$

$textbf{The zeros are $-90^0$ and $-270^0$}$.

(a) $-dfrac{3}{2}$ and $2$ ; (b) $0$ is $1$,so $x=0$; (c) $45^0$ and $225^0$; (d) $-90^0$ and $-270^0$

#### (a)

Here we have $textbf{vertically stretch}$ by a factor of $dfrac{1}{2}$.

#### (b)

Here we have $textbf{vertically stretch}$ by a factor of $2$ and $textbf{translation}$ $4$ units right.

#### (c)

Here we have $textbf{vertically stretch}$ by a factor of $-3$ and $textbf{translation}$ $7$ units up.

#### d)

Here we have $textbf{vertically stretch}$ by a factor of $5$ and $textbf{translation}$ $3$ units right and $2$ units down.

Mark with $B_0=1000$$,$r=0.08$,$B_t$amount of money after$t$years.\
subsection*{(a)}
The equation for the amount of money after$t$years is:\$B_t=B_0(1+r)^t$\
subsection*{(b)}
After$3$years, we will have:\$B_3=B_0(1+r)^3=1000(1+0.08)^3=1000cdot1.26=1259.712
$$
subsection*{(c)}
The amount of money doesn’t increase constantly because we calculate $8%$ of money per year on different amounts each year. That amount is bigger and bigger every year,but not for the same amount of money.
$$

#### (a)

We can see from the following graph of this function which is the maximum and minimum height, and $textbf{the minimum height}$ is $1m$ and $textbf{the maximum height}$ is $15m$.

#### (b)

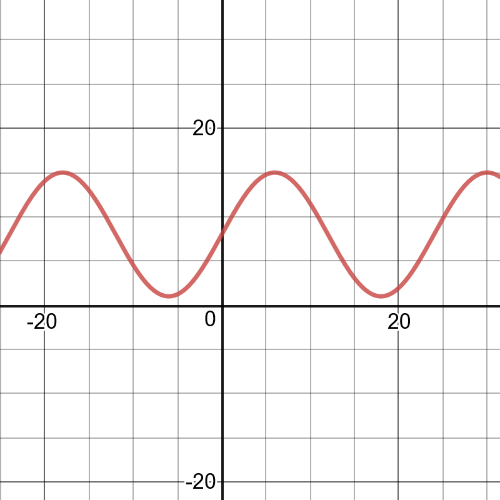
Let’s calculate for what time the seat will reach the highest point on Ferris wheel, that is $15m$:

$15=8+7sin{(15°t)}$

$7sin{(15°t)}=7$

$sin{(15°t)}=1$

$15°t=arcsin1$

$t=dfrac{1}{15°}arcsin1$

$t=343,95s$

Here, we used that $15°=dfrac{pi}{12}$.

We get that time for which the seat reach the highest point from the start is $t=343,95s$, and from that heighest point to the start point is needed the same time, because it is a wheel, $textbf{so we conclude that the time needed for seat to get to the start point again for one ride is}$:

$t=2cdot343,95=687,9s$

#### (c)

Here we have:

$$
h(x)=8+7sin(dfrac{pi}{12}30)=8+7sin(dfrac{15}{6}pi)=8.95m
$$

(b) $687,9s$; (c) $8.95m$