#### (a)

$textbf{This relation is a function}$, because its graph passes vertical line test.

#### (b)

$textbf{Its domain and range}$ is following set:

$D=R=Bbb{R}$

(a)$textbf{It is a function}$; (b) $D=R=Bbb{R}$

#### (a)

$textbf{Possible parent function}$ could be a function $y=x^2$.

#### (b)

Here we have graph of $textbf{possible function $y=x^2-2$}$:

#### (c)

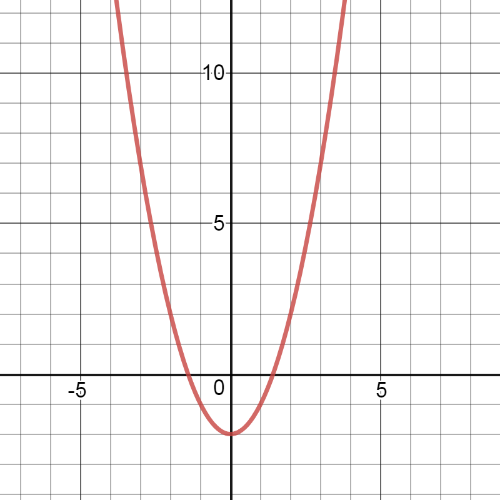
$textbf{The transformation}$ which is made here is $textbf{translation 2 units down}$.

$textbf{Even function}$ is that function for which $f(-x)=f(x)$, so, now we will prove that for given function in this task:

$$
f(-x)=left|3(-x) right|+(-x)^2=left|-3x right|+x^2=left|3x right|+x^2=f(x)
$$

$$
f(-x)=left|3(-x) right|+(-x)^2=left|-3x right|+x^2=left|3x right|+x^2=f(x)
$$

Here we have $textbf{different characteristics}$ of those two functions:

Function $y=x^2$:

This function is $textbf{decreasing}$ on $left(-infty,0 right)$ and $textbf{increasing}$ on $left[0,infty right)$, it has $textbf{one zero}$ in $x=0$ and it is $textbf{even}$ function.

Function $y=2^x$:

This function is $textbf{increasing}$ on its domain, $textbf{it has no zeros}$ and this fuction is $textbf{neither function}$.

This transformations are: $textbf{vertical stretch}$ by a factor of $-1$, $textbf{translation}$ $3$ units left and $5$ units down.

On the following picture is $textbf{graph}$ of this transfpremd function:

Here we have $textbf{horizontal compression}$ by a factor of $2$ and $textbf{translation}$ $1$ unit up. $textbf{The algebraic representation is}$:

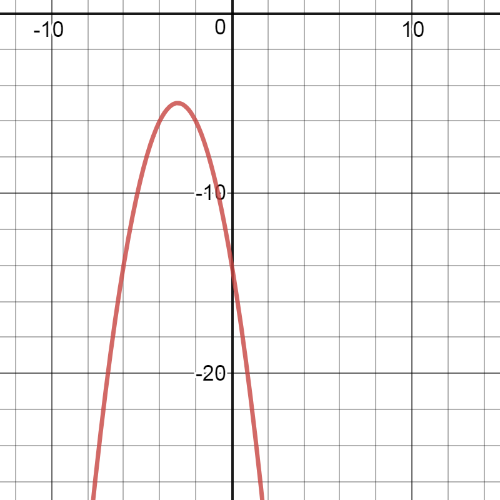
$$
y=left|dfrac{1}{2}x right|+1
$$

$$
y=left|dfrac{1}{2}x right|+1
$$

#### (a)

First, we will transform a little given function:

$3f(-x+1)+2=3f(-(x-1))+2$,
so we have following transformation of coordinates of given point:

$left(3,5 right)rightarrowleft(-1cdot3,3cdot5 right)=left(-3,15 right)$

$left(-3,15 right)rightarrowleft(-3+1,15+2 right)=left(-2,17 right)$

So, $textbf{corresponding point}$ is $left(-2,17 right)$.

#### (b)

Here we have actually $textbf{inverse function}$, so transformation is:

$$
left(3,5 right)rightarrowleft(5,3 right)
$$

(a) $left(-2,17 right)$; (b) $left(5,3 right)$

Here we have next:

$y=-2(x+1)=-2x-2$

$x=-2y-2$

$-2y=x+2$

$y=-dfrac{1}{2}(x+2)$

So, $textbf{inverse function}$ is $y=dfrac{1}{2}(x+2)$

$y=dfrac{1}{2}(x+2)$

#### (a)

How we have in this task that $125000$>50000$$, we have tax,$x$, of$12%$, so, the solution is next:\$x=$dfrac{12cdot125000}{100}$=15000
$$
\

textbf{So, the tax is} $15000
$$

#### (b)

$textbf{Function which describes this model os tax policy}$ would be following:

$$
f(x)=begin{cases}
dfrac{5}{100}x & xleq50000\\

dfrac{12}{100}x & x>50000\
end{cases}
$$

(a) $15000$$;\

(b)$f(x)=
$$
begin{cases}
dfrac{5}{100}x & xleq50000\\

dfrac{12}{100}x & x>50000\
end{cases}
$$
$

#### (a)

Here we have $textbf{graph}$ of this function:

#### (b)

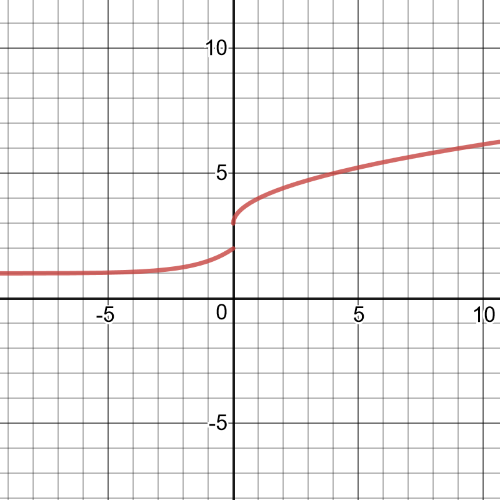
This function is $textbf{discontinuous}$ on its entire domain because all the pieces of the function not join together at the endpoints of the given intervals.

#### (c)

This function is $textbf{increasing}$ on its entire domain.We can see that from the graph of this function from part $(a)$.

#### (d)

$textbf{The domain}$ of this function is set $D=Bbb{R}$ and $textbf{range}$ is set $R=left(0,infty right)$.

(b) $textbf{discontinuous}$; (c) $textbf{increasing on its entire domain}$;

(d)$D=Bbb{R}$, $R=left(0,infty right)$