#### (a)

$textbf{This is a function}$ because it passes the vertical line test, that we can see from the graph of this function.

Its domain is set $D=Bbb{R}$ and its range is set $R=Bbb{R}$.

#### (b)

$textbf{This is a function}$ because it passes the vertical line test, that we can see from the graph of this function.

Its domain is set $D=Bbb{R}$ and its range is set $R=left(-infty,3 right]$.

#### (c)

$textbf{This is not a function}$ because it doesn’t pass the vertical line test, that we can see from the graph of this function.

Its domain is set $D=Bbb{R}$ and its range is set $R=Bbb{R}$.

#### (d)

$textbf{This is a function}$ because it passes the vertical line test, that we can see from the graph of this function.

Its domain is set $D=left[0,infty right)$ and its range is set $R=Bbb{R}$.

#### (a)

That would be a function $y=30+0.02x$

#### (b)

$textbf{The domain}$ of this function is $D=Bbb{R}$ and the range is $R=Bbb{R}$

(a)$y=30+0.02x$; (b)$D=R=Bbb{R}$

$textbf{The domain}$ of this function is set $D=Bbb{R}$ and $textbf{the range is}$ the set $R=left[-1,infty right)$

On the following picture is $textbf{graph}$ of this function:

$D=Bbb{R}$; $R=left[-1,infty right)$

We had explanation of this function and its definition in $textbf{chapter }1.2$, and according to it, we have that solution of this task is following interval:

$left|x right|leq2$

$$
left|x right|leq2
$$

#### (a)

For those two functions we have that the things they have $textbf{in common}$ are:

Their $textbf{domain}$ is set $D=Bbb{R}$ and both are $textbf{continious}$ functions.

Things that $textbf{distinguishes}$ between them are:

$textbf{The range}$ of function $f(x)$ is set $R=left[0,infty right)$, it has $textbf{one zero}$ and it is $textbf{even}$ function. $textbf{The range}$ of function $g(x)$ is $R=left[-1,1 right]$, it has $textbf{infinite number of zeros}$ and it is $textbf{odd function}$.

#### (b)

For those two functions we have that the things they have $textbf{in common}$ are:

Both are $textbf{odd}$ functions.

Things that $textbf{distinguishes}$ between them are:

$textbf{The domain}$ of function $g(x)$ is set $D=Bbb{R}$ and $textbf{the range}$ is set $R=Bbb{R}$, it has $textbf{one zero}$ and it is $textbf{continuous}$ function. $textbf{The domain}$ and $textbf{the range}$ of function $f(x)$ is $R=Bbb{R}/left{0 right}$, it has $textbf{no zeros}$ and it is $textbf{discontinuous}$ function.

#### (c)

For those two functions we have that the things they have $textbf{in common}$ are:

Their $textbf{domain}$ is set $D=Bbb{R}$ and $textbf{the range}$ is set $R=left[0,infty right)$, both are $textbf{continious, odd}$ functions, and both have $textbf{one zero}$, they are $textbf{decreasing}$ on $left(-infty,0 right]$ and $textbf{increasing}$ on $left(0,infty right)$

There is no things that $textbf{distinguishes}$ between them.

#### (d)

For those two functions we have that the things they have $textbf{in common}$ are:

Their $textbf{domain}$ is set $D=Bbb{R}$ and both are $textbf{continious}$ functions, both are $textbf{increasing}$ on $left[1,infty right)$.and they are $textbf{positive}$ functions.

Things that $textbf{distinguishes}$ between them are:

Function $f(x)$ is $textbf{odd}$ function. Function $g(x)$ is $textbf{even}$ function.

#### (a)

$textbf{The domain}$ of this fuction is set $D=Bbb{R}$ and $textbf{the range}$ is also set $R=Bbb{R}$.

On the interval $left(-infty,infty right)$, or on its whole domain, this function is $textbf{increasing}$.

Graph of this function is $textbf{symmetric with respect to the coordinate start}$.

#### (b)

$textbf{The domain}$ of this fuction is set $D=Bbb{R}$ and $textbf{the range}$ is set $R=left[2,infty right)$.

On the interval $left(-infty,2 right)$ this function is $textbf{decreasing}$, and on the interval $left[2,infty right)$ this function is $textbf{increasing}$.

Graph of this function is $textbf{symmetric with respect to the $y$-axis}$.

#### (c)

$textbf{The domain}$ of this fuction is set $D=Bbb{R}$ and $textbf{the range}$ is set $R=left[1,infty right)$.

On the interval $left(-infty,infty right)$, or on the whole its domain, this function is $textbf{increasing}$.

Graph of this function is $textbf{not symmetric}$.

(a) $D=R=Bbb{R}$, $left(-infty,infty right) uparrow$, symmetric with respect to the coordinate start; (b) $D=Bbb{R}$, $R=left[2,infty right]$, $left(-infty,2 right) downarrow$, $left[2,infty right) uparrow$,symmetric with respect to the $y$-axis; (c) $D=Bbb{R}$, $R=left[1,infty right)$, $left(-infty,infty right) uparrow$, it is not
symmetric

#### (a)

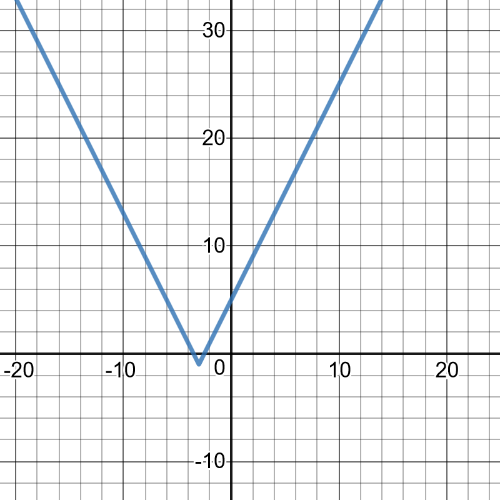
$textbf{The parent function}$ is $y=left|x right|$.

$textbf{The transformations}$ which we have here are only $textbf{translation}$ 1 unit to the right.

On the following picrure is $textbf{graph}$ of this transformed function:

#### (b)

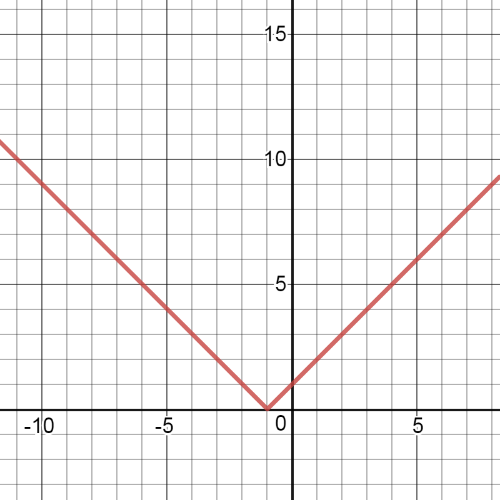
$textbf{The parent function}$ is $y=sqrt{x}$.

$textbf{The transformations}$ which we have here are $textbf{horizontal compression}$ by a factor of $dfrac{1}{3}$, $textbf{vertical stretch}$ by a factor of $-0.25$, $textbf{translation}$ 7 units to the left.

On the following picrure is $textbf{graph}$ of this transformed function:

#### (c)

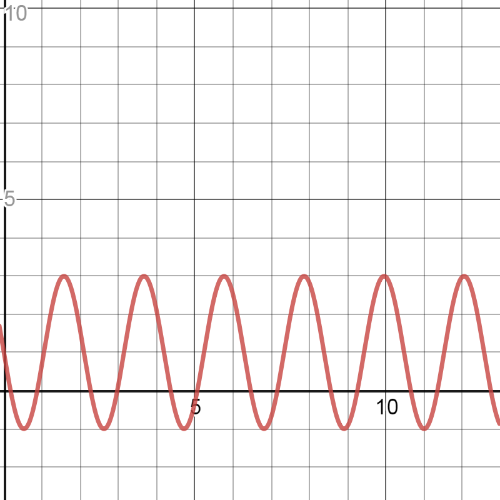
$textbf{The parent function}$ is $y=sin{x}$.

$textbf{The transformations}$ which we have here are $textbf{horizontal compression}$ by a factor of $dfrac{1}{3}$, $textbf{vertical stretch}$ by a factor of $-2$, $textbf{translation}$ 1 unit down.

On the following picrure is $textbf{graph}$ of this transformed function:

#### (d)

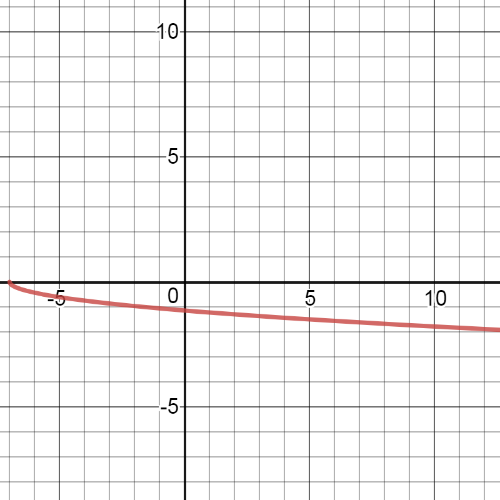
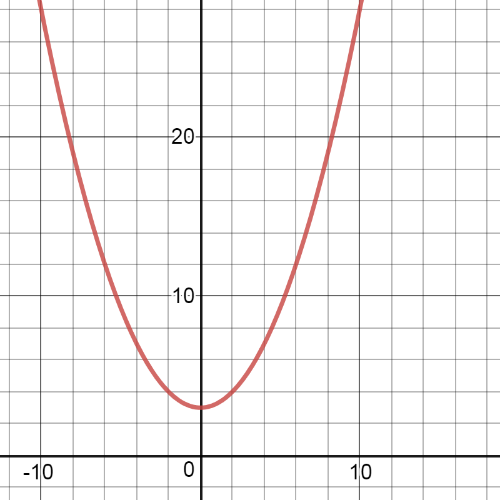
$textbf{The parent function}$ is $y=2^x$.

$textbf{The transformations}$ which we have here are $textbf{horizontal compression}$ by a factor of $-dfrac{1}{2}$, $textbf{translation}$ 3 units up.

On the following picrure is $textbf{graph}$ of this transformed function:

According to transformations given in this task, we have that $textbf{transformed function is}$:

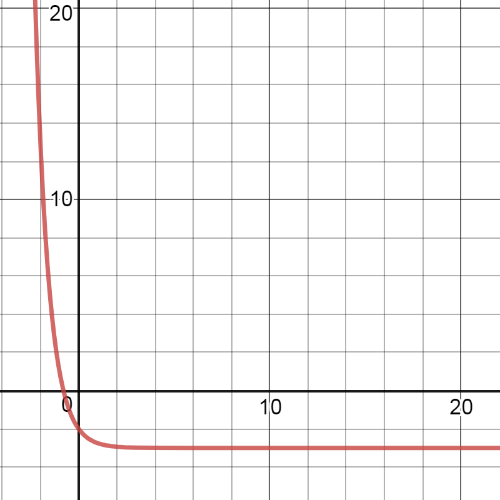
$y=(dfrac{1}{2}x)^2+3=dfrac{1}{4}x^2+3$

On the following picture is $textbf{the graph}$ of this transformed function:

$y=(dfrac{1}{2}x)^2+3=dfrac{1}{4}x^2+3$

#### (a)

According to explanation of transformation step by step of coordinates on page $34$, we have next:

$left(2,1 right)=left({-1}cdot{2},{-1}cdot{1} right)=left(-2,-1 right)$

$left(-2,-1 right)=left(-2,-1+2 right)=left(-2,1 right)$

So, $textbf{the corresponding point}$ on the graph of thi transformed function is $left(-2,1 right)$.

#### (b)

According to explanation of transformation step by step of coordinates on page $34$, we have next:

$left(2,1 right)=left({-dfrac{1}{2}}cdot{2},1 right)=left(-1,-1 right)$

$left(-1,-1 right)=left(-1-9,1-7 right)=left(-10,-6right)$

So, $textbf{the corresponding point}$ on the graph of thi transformed function is $left(-10,-6 right)$.

#### (c)

According to explanation of transformation step by step of coordinates on page $34$, we have next:

$left(2,-1 right)=left(2+2,1+2 right)=left(4,3right)$

So, $textbf{the corresponding point}$ on the graph of thi transformed function is $left(4,3right)$.

#### (d)

According to explanation of transformation step by step of coordinates on page $34$, we have next:

$left(2,1 right)=left({dfrac{1}{5}}cdot{2},1cdot0.3 right)=left(dfrac{2}{5},0.3 right)$

$left(dfrac{2}{5}-3,0.3right)=left(-dfrac{13}{5},0.3 right)$

So, $textbf{the corresponding point}$ on the graph of thi transformed function is $left(-dfrac{13}{5},0.3 right)$.

#### (e)

First, we will transform a little this function in order to be easier to notice which transformation are made:

$y=1-f(1-x)=-f(-(x-1))+1$

According to explanation of transformation step by step of coordinates on page $34$, we have next:

$left(2,1 right)=left({-1}cdot{2},{-1}cdot{1} right)=left(-2,-1 right)$

$left(-2,-1 right)=left(-2+1,-1+1 right)=left(-1,0 right)$

So, $textbf{the corresponding point}$ on the graph of thi transformed function is $left(-1,0 right)$.

#### (f)

According to explanation of transformation step by step of coordinates on page $34$, we have next:

$left(2,1 right)=left({dfrac{1}{2}}cdot{2},-1cdot1 right)=left(1,-1 right)$

$left(1,-1 right)=left(1+8,-1 right)=left(9,-1right)$

So, $textbf{the corresponding point}$ on the graph of thi transformed function is $left(9,-1 right)$.

(a) $left(-2,1 right)$; (b) $left(-10,-6 right)$; (c) $left(4,3 right)$; (d) $left(-dfrac{13}{5},0.3 right)$; (e) $left(-1,0 right)$; (f) $left(9,-1 right)$

We have that $textbf{if point $left(x,y right)$
represents a point on the graph of fuction $f$,
then $left(y,x right)$
represents a point on the graph of the inverse function}$, $f^{-1}$. According to this, we have that solutions of this task are:

#### (a)

$textbf{The point which corresponds the graph of inverse function is}$ $left(2,1 right)$.

#### (b)

$textbf{The point which corresponds the graph of inverse function is}$ $left(-9,-1 right)$.

#### (c)

$textbf{The point which corresponds the graph of inverse function is}$ $left(7,0 right)$.

#### (d)

Here have actually point $left(5,7 right)$.

$textbf{The point which corresponds the graph of inverse function is}$ $left(7,5 right)$.

#### (e)

Here have actually point $left(0,-3 right)$.

$textbf{The point which corresponds the graph of inverse function is}$ $left(-3,0 right)$.

#### (f)

Here have actually point $left(1,10right)$.

$textbf{The point which corresponds the graph of inverse function is}$ $left(10,1 right)$.

(a) $left(2,1 right)$; (b) $left(-9,-1 right)$; (c) $left(7,0 right)$; (d) $left(7,5 right)$; (e) $left(-3,0 right)$; (f) $left(10,1 right)$;

$textbf{
The range of the original function becomes the domain of the inverse function, and the domain of the original function becomes the range of the inverse function}$, and we have the following:

#### (a)

$textbf{The domain}$ of the inverse function is:

$D=left{xinBbb{R}|-2<{x}<2 right}$

And $textbf{the range}$ is:

$R=left{xinBbb{R} right}$

#### (b)

$textbf{The domain}$ of the inverse function is:

$D=left{xinBbb{R}||{x}<12 right}$

And $textbf{the range}$ is:

$R=left{xinBbb{R}|{x}geq7 right}$

(a)$D=left{xinBbb{R}|-2<{x}<2 right}$, $R=left{xinBbb{R} right}$;

(b)$D=left{xinBbb{R}||{x}<12 right}$, $R=left{xinBbb{R}|{x}geq7 right}$

Here we find an inverse relation $textbf{by replacing the places}$ $x$ and $y$, as explained on page $41$, so we have next:

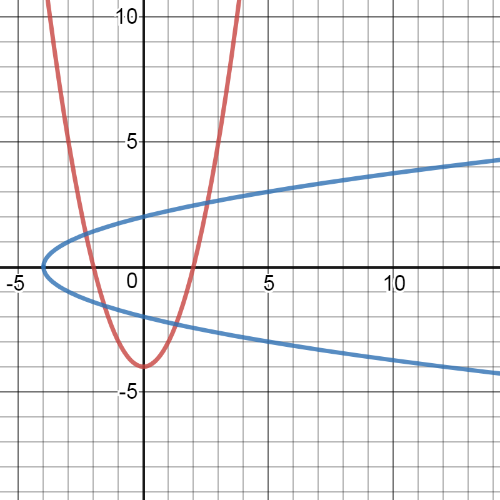
#### (a)

$y=x^2-4$

$x=y^2-4$

$y^2=x+4$

$y=-sqrt{x+4}$ $vee$ $y=sqrt{x+4}$

Here we have that $textbf{inverse relation is not a function}$ because it can be split into the two functions.

On the following picture, red graph is the graph of origin function and the blue graph is graph of inverse relation:

#### (b)

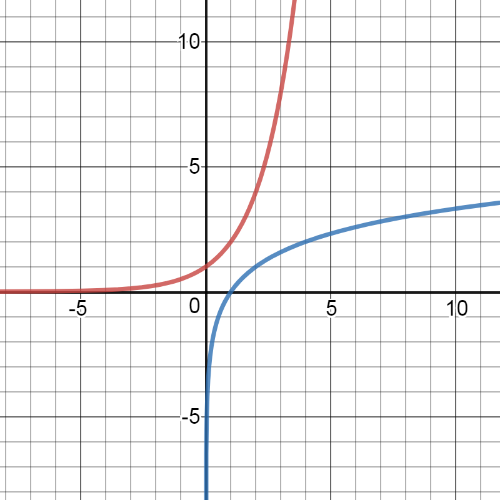
$y=2^x$

$x=2^y$

$y=log_2 x$

Here, $textbf{the inverse relation is a function}$, and on the following picture its graph is blue, while the graph of the origin function is blue:

Here we find an inverse function $textbf{by replacing the places}$ $x$ and $y$, as explained on page $41$.

#### (a)

$y=2x+1$

$x=2y+1$

$2y=x-1$

$y=dfrac{1}{2}(x-1)$

#### (b)

$y=x^3$

$x=y^3$

$y=sqrt[3]{x}$

(a) $y=dfrac{1}{2}(x-1$; (b) $y=sqrt[3]{x}$

On the following picture is $textbf{the graph}$ of this function, we can see that this is $textbf{continuous}$ function and its $textbf{domain and range}$ is set $D=R=Bbb{R}$:

We can find algebraic representation of this function using its graph given in task and creating table of values, and on that way we have that the solution of this task is $textbf{following function:}$

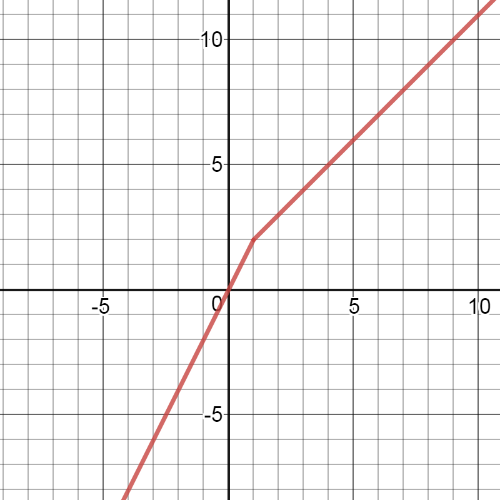
$$
f(x)begin{cases}
3x-1 & {x}leq2\
-x & x>2\
end{cases}
$$

$$
f(x)begin{cases}
3x-1 & {x}leq2\
-x & x>2\
end{cases}
$$

This $textbf{is not continuous function}$ in $x=1$ because its pieces not join together at the endpoints of the given intervals, which we can see from following graph:

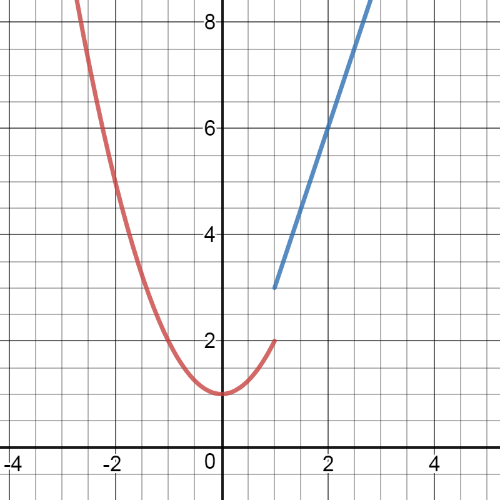
$$
textbf{Not continuous}
$$

#### (a)

According to the text of the task, we have $textbf{following function:}$

$$
f(x)=begin{cases}
30 & {x}leq200\
30+0.03(x-200) & x>200\
end{cases}
$$

#### (b)

How we have that $350>200$, we will use second function to calculate this price, $y$:

$y=30+0.03(350-200)=30+0.03cdot150=30+4.5=34.5$

#### (c)

How we have that $180leq200$, we will use first function to calculate this price, $y$:

$y=30$

(a)
$$
f(x)=begin{cases}
30 & {x}leq200\
30+0.03(x-200) & x>200\
end{cases}
$$

(b) 34.5; (c) 30

Here, we have that domain of $f$ is set $left{0,1,4,5 right}$ and the domain of $g$ is set $left{-1,1,2,4,8 right}$, so, for operations with those functions we have that $textbf{shared domain}$ is set $left{1,4 right}$.

#### (a)

Here, on shared domain $left{1,4 right}$ we have next:

$f(1)+g(1)=3+4=7$

$f(4)+g(4)=7+8=15$

#### (b)

On share domain, $left{1,4 right}$ is:

$f(1)-g(1)=3-4=-1$

$f(4)-g(4)=7-8=-1$

#### (c)

Here we have next:

$f(1)g(1)=3cdot4=12$

$f(4)g(4)=7cdot8=56$

#### (a)

Here we have $textbf{the graph}$ of the function $f$:

#### (b)

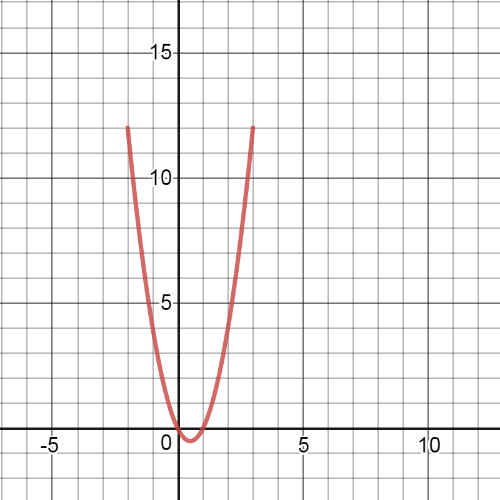
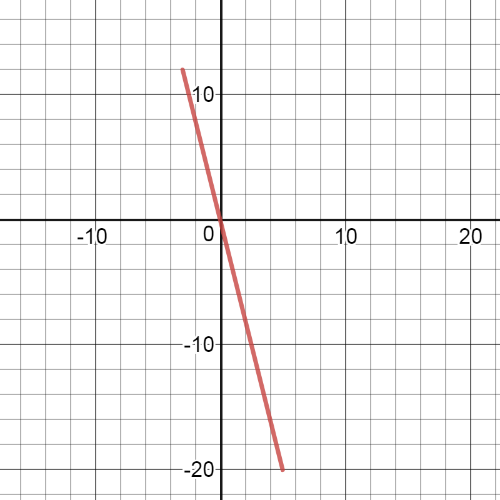
Here we have $textbf{the graph}$ of the function $g$:

#### (c)

Here we have $textbf{the graph of the function $f+g$ on shared domain}$ $left{-2leq{x}leq3 right}$:

#### (d)

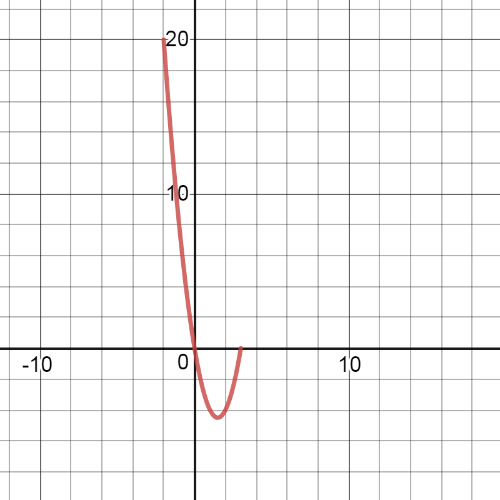
Here we have $textbf{the graph pf the function$f-g$ on shared domain}$ $left{-2leq{x}leq3 right}$:

#### (e)

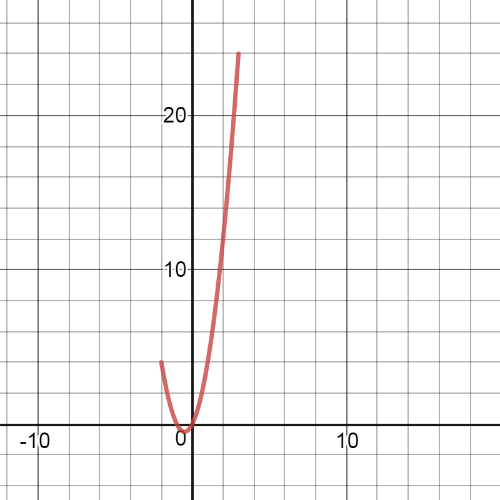
Here we have $textbf{the graph of the function $fg$ on shared domain}$ $left{-2leq{x}leq3 right}$:

Find first which are the functions $f+g$, $f-g$, $g-f$, $fg$, and then we will match answer with the operation.

$f(x)+g(x)=x^2+2x+x+1=x^2+3x+1$

$f(x)-g(x)=x^2-+2x-(x+1)=x^2+2x-x-1=x^2+x-1$

$g(x)-f(x)=x+1-(x^2+2x)=x+1-x^2-2x=-x^2-x+1$

$f(x)g(x)=(x^2+2x)(x+1)=x^3+x^2+2x^2+2x=x^3+3x^2+2x$

So, $textbf{the answers are}$:

(a)$rightarrow$D

(b)$rightarrow$C

(c)$rightarrow$A

(d)$rightarrow$B

(a)$rightarrow$D;(b)$rightarrow$C;(c)$rightarrow$A;(d)$rightarrow$B

#### (b)

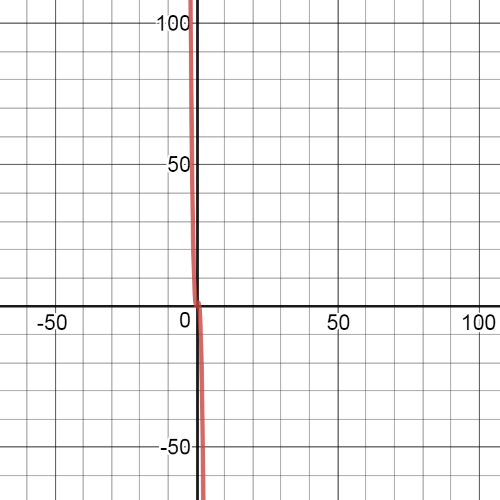
On the following picture are $textbf{graphs}$ of functions $f$ and $g$.Red one is graph of the function $f$ and blue one is the graph of $g$:

#### (c)

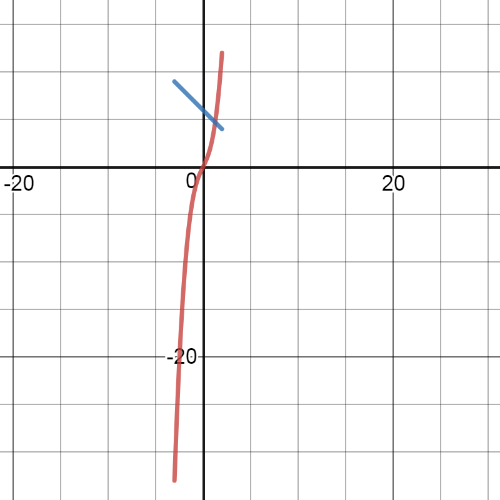
First, let find the equation of $f+g$:

$f(x)+g(x)=x^3+2x^2-x+6$

On the following picture from part $(b)$, green one is $textbf{graph of the function}$ $f+g$:

#### (d)

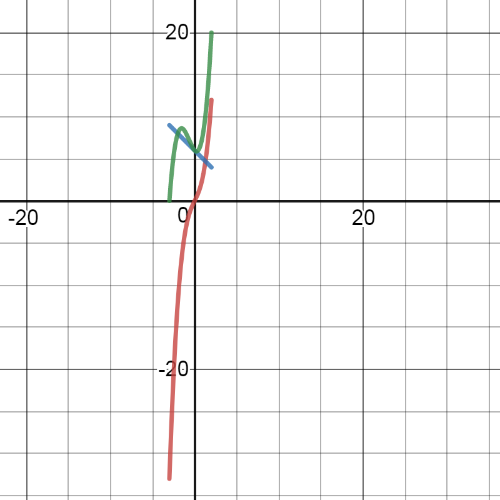
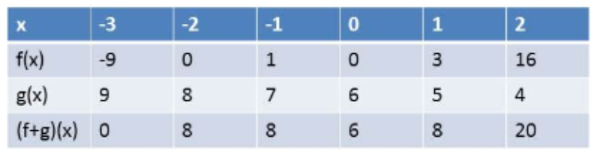
For examlple, we will use $x=0$ and $x=1$, according to the equation from part $(c)$, we have:

$f(0)+g(0)=0^3+2cdot0-0+6=6$

$f(1)+g(1)=1^3+2cdot1-1+6=8$

And from the table we can see that $textbf{those values are matching}$, so, the equation from part $(c)$ is correct.