$A(r)=4 pi r ^2$

#### (b)

$V=dfrac{4}{3}pi r^3$

$dfrac{3V}{4pi}=r^3$

$sqrt[3]{dfrac{3V}{4pi}}=r$

So, $r(V)=sqrt[3]{dfrac{3V}{4pi}}$

#### (c)

$A(r(V))=Aleft(sqrt[3]{dfrac{3V}{4pi}} right)$

$=4pileft(sqrt[3]{dfrac{3V}{4pi}} right)^2$

$=4pileft(dfrac{3V}{4pi} right)^{dfrac{2}{3}}$

#### (d)

$$
4pileft( dfrac{3(0.75)}{4pi}right)^{dfrac{2}{3}}=4m^2
$$

Fromt he following graph we can see that $textbf{solution}$ is $-1.62 leq x leq 1.62$.

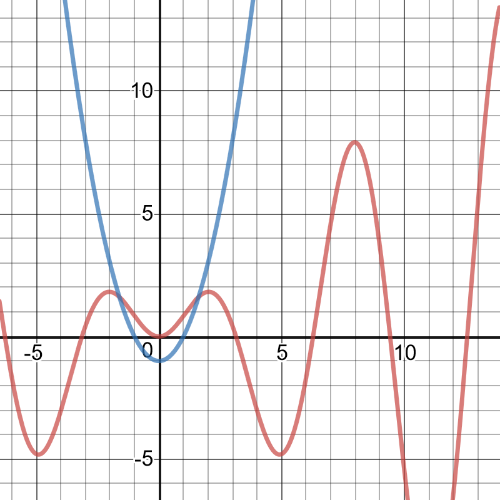
$g(x)=(x+3)^7$ and $h(x)=2x$

Use a graphing calculator to detrmine the regression equation.

$N(n)=1n^3+8n^2+40n+400$

#### (b)

$N(3)=1(3)^3+8(3)^2+40(3)+400=27+72+120+400=619$

$-3=6(2)+b$

$-3=12+b$

$-15=b$

So,$f(x)=6x-15$

$g(x)=5(x+8)^2-1$

$(ftimes g)(x)=(6x-15)(5(x+8)^2-1)$

$=(6x-15)(5(x^2+16x+64)-1)$

$=(6x-15)(5x^2+80x+320-1)$

$=(6x-15)(5x^2+80x+319)$

$=30x^3+405x^2+714x-4785$

There is a horizontal asymptote of $y=275cm$. This is the maximum height this species will reach.

#### (b)

$150=dfrac{275}{1+26(0.85)^t}$

$150(1+26(0.85)^t)=275$

$26(0.85)^t=(275div 150)-1$

$26(0.85)^t=0.8333$

$(0.85)^t=0.03205$

$tlog0.85=log 0.03205$

$t=21.2$ months

$5x+18=2x^2$

$2x^2-5x-18=0$

$(2x-9)(x+2)=0$

$x=4.5$ or $x=-2$

Negative answers do not make sense in this context, so, $textbf{the answer is}$ $x=4.5$ or $4500$ items.

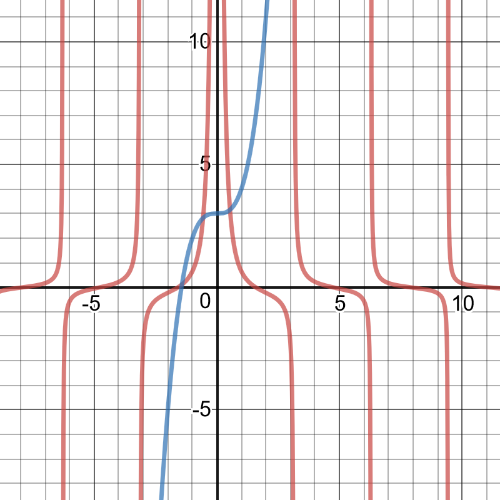
From the following graph, we can see that $textbf{the solutions}$ are:

$x=-3.1, x=-1.4, x=-0.6, x=0.5, x=3.2$.