
All Solutions
Page 576: Practice Questions
Since shop $1$ contains $-1.4t^2$, it sales are decreasing after $2000$.Since shop $2$ contains all addition, its sales are increasing after $2000$.
#### (b)
$S_{1+2}=700-1.4t^2+t^3+3t^2+500=t^3+1.6t^2+1200$
#### (c)
$t=6:t^3+1.6t^2+1200=(6)^3+1.6(6)^2+1200=216+1.6(36)+1200$
$=216+57.6+1200=1473.6$ thousand or $1 473 600$
#### (d)
The owner should close the first shop, because the sales are decreasing and will eventually reach zero.
$C(x)=9.45x+52000$
#### (b)
$I(x)=15.8x$
#### (c)
$P(x)=I-C=15.8x-(9.45x+52000)=15.8x-9.45x-52000=6.35x-52000$
$(ftimes g)(x)=3tan(7x)times 4cos(7x)=12sin(7x)$
#### (b)
$(ftimes g)(x)=sqrt{3x^2}times 3sqrt{3x^2}=3(3x^2)=9x^2$
#### (c)
$(ftimes g)(x)=(11x-7)(11x+7)=121x^2-49$
#### (d)
$(ftimes g)(x)=ab^x times 2ab^{2x}=2a^2b^{3x}$
$Ctimes A=(15000 000(1.01)^t)(2850+200t)$
$=42 750 000 000(1.01)^t + 3 000 000 000t(1.01)^t$
#### (b)
$$
42750000000(1.01)^{26}+3000000000cdot26(1.01)^{26}=156402200032.31$
$$
$Ctimes A = 42 750 000 000(1.01)^t + 3 000 000 000t(1.01)^t$; (c) $156402200032.31$$
$(f div g)(x)=105x^3 div 5x^4=dfrac{21}{x}$
#### (b)
$(f div g)(x)=(x-4)div(2x^2+x-36)=(x-4)div(x-4)(2x+9)=dfrac{1}{2x+9}$
#### (c)
$(fdiv g)(x)=sqrt{x+15}div (x+15)=dfrac{sqrt{x+15}}{x+15}$
#### (d)
$$
(fdiv g)(x)=11x^5 div 22x^2 log x=dfrac{x^3}{2log x}
$$
$left{xinBbb{R}|x ne 0right}$
#### (b)
$left{xinBbb{R}|xne 4, xne -dfrac{9}{2} right}$
#### (c)
$left{xinBbb{R}|x > -15 right}$
#### (d)
$left{xinBbb{R}| x>0 right}$
Domain of $f(x): left{xinBbb{R}|x >-1 right}$
Range of $f(x): left{yinBbb{R}|y>0 right}$
Domain of $g(x): left{xinBbb{R} right}$
Range of $g(x): left{yinBbb{R}|ygeq 3 right}$
#### (b)
$f(g(x))=f(x^2+3)=dfrac{1}{sqrt{x^2+3+1}}=dfrac{1}{sqrt{x^2+4}}$
#### (c)
$g(f(x))=gleft(dfrac{1}{sqrt{x+1}} right)$
$=left(dfrac{1}{sqrt{x+1}} right)^2+3$
$=dfrac{1}{x+1}+3$
$=dfrac{1}{x+1}+dfrac{3x+3}{x+1}=dfrac{3x+4}{x+1}$
$f(g(0))=dfrac{1}{sqrt{0^2+4}}=dfrac{1}{sqrt{4}}=dfrac{1}{2}$
#### (e)
$g(f(0))=dfrac{3(0)+4}{0+1}=dfrac{4}{1}=4$
#### (f)
For $f(g(x)): left{xinBbb{R} right}$
For $g(f(x)): left{xinBbb{R}|x>-1 right}$
$(f circ f)(x)=f(x-3)=x-3-3=x-6$
#### (b)
$(f circ f circ f)(x)=f(x-6)=x-6-3=x-9$
#### (c)
$(f circ f circ f circ f)(x)=f(x-9)=x-9-3=x-12$
#### (d)
$f$ composed with itself $n$ times $=x-3(1+n)$
$A(r)=pi r^2$
#### (b)
$r(C)=dfrac{C}{2 pi}$
#### (c)
$A(r(C))=Aleft(dfrac{C}{2 pi} right)=pi left(dfrac{C}{2 pi} right)^2$
$=pileft(dfrac{C^2}{4 pi ^2} right)=dfrac{C^2}{4 pi}$
#### (d)
$$
dfrac{C^2}{4 pi}=dfrac{(3.6)^2}{4 pi}=1.03m
$$
$f(x)<g(x): -1.2<x1.2$
$f(x)=g(x): x=-1.2, 0$ or $1.2$
$f(x)>g(x): x<-1.2$ or $0<x<1.2$
$-3csc x=x$
Try $x=3$:$-3csc 3=3$
$-21.3=3$
Try $x=4: -3csc4=4$
$3.9=4$
So, $x=4.0$
#### (b)
$cos^2x=3-2sqrt{x}$
Try $x=1: cos^2 1=3-2sqrt{1}$
$0.29=3-2(1)$
$0.29=1$
Try $x=2: cos^2 2=3-2sqrt{2}$
$0.17=0.17$
So, $x=2.0$
$8^x=x^8$
Try $x=-0.7: 8^{-0.7}=(-0.7)^8$
$0.23=0.06$
Try $x=-0.8:8^{- 0.8}=(-0.8)^8$
$0.19=0.17$
So, $x=-0.8$
#### (d)
$7sin x=dfrac{3}{x}$
Try $x=0.6: 7sin(0.6)=dfrac{3}{0.6}$
$3.95=5$
Try $x=0.7: 7sin(0.7)=dfrac{3}{0.7}$
$4.5=4.3$
So, $x=0.7$.
The rate of change is $(3200-2000)div(7-5)$ or $600$ frogs per year. So, the equation is :
$P(t)=600t-1000$
The slope is the rate at which the population is changinng.
#### (b)
$P(t)=617.6(1.26)^t$
$617.6$ is the initial population and $1.26$ represents the growth.
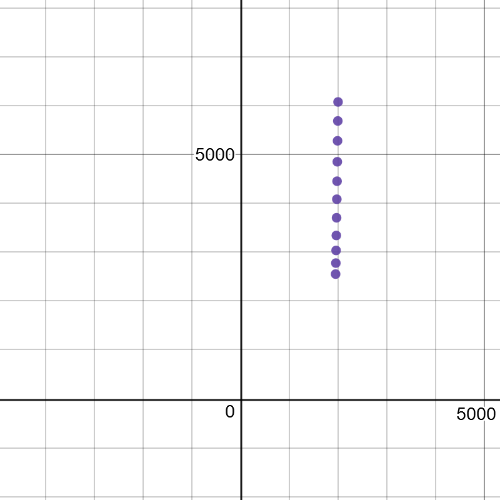
$t=13 Rightarrow P(t)=3242$
$t=23 Rightarrow P(t)=3875$
$t=90 Rightarrow P(t)=12806$

