
All Solutions
Page 56: Check Your Understanding
#### (a)
$textbf{The domain}$ of $f+g$ is actually set made of shared domain of those two functions,it is set $D=left{-4,-2,1,4 right}$.
So,we have next:
$(f+g)(-4)=f(-4)+g(-4)=4+2=6$
$(f+g)(-2)=f(-2)+g(-2)=4+1=5$
$(f+g)(1)=f(1)+g(1)=3+2=5$
$(f+g)(4)=f(4)+g(4)=6+4=10$
So, $f+g=left{left(-4,6 right),left(-2,5 right),left(1,5 right),left(4,10 right) right}$.
#### (b)
$textbf{The domain}$ of $f-g$ is actually set made of shared domain of those two functions,it is set $D=left{-4,-2,1,4 right}$.
So,we have next:
$(f-g)(-4)=f(-4)-g(-4)=4-2=2$
$(f-g)(-2)=f(-2)-g(-2)=4-1=3$
$(f-g)(1)=f(1)-g(1)=3-2=1$
$(f-g)(4)=f(4)-g(4)=6-4=2$
So, $f+g=left{left(-4,2 right),left(-2,3 right),left(1,1 right),left(4,2 right) right}$.
$textbf{The domain}$ of $g-f$ is actually set made of shared domain of those two functions,it is set $D=left{-4,-2,1,4 right}$.
So,we have next:
$(g-f)(-4)=g(-4)-f(-4)=2-4=-2$
$(g-f)(-2)=g(-2)-f(-2)=1-4=-3$
$(g-f)(1)=g(1)-f(1)=2-3=-1$
$(g-f)(4)=g(4)-f(4)=4-6=-2$
So, $f+g=left{left(-4,-2 right),left(-2,-3 right),left(1,-1 right),left(4,-2 right) right}$.
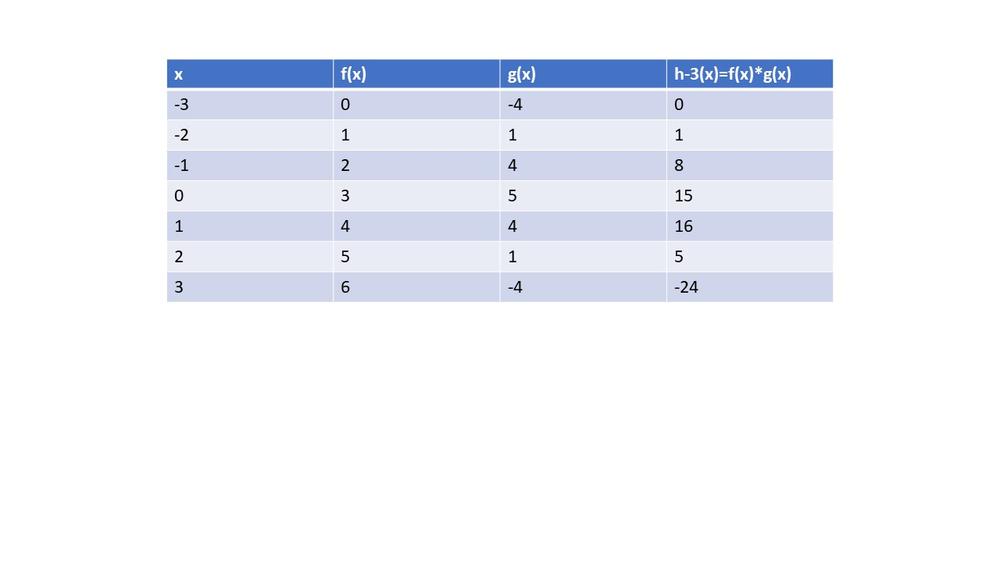
#### (d)
$textbf{The domain}$ of $fg$ is actually set made of shared domain of those two functions,it is set $D=left{-4,-2,1,4 right}$.
So,we have next:
$(fg)(-4)=f(-4)g(-4)=2cdot4=8$
$(fg)(-2)=f(-2)g(-2)=1cdot4=4$
$(fg)(1)=f(1)g(1)=2cdot3=6$
$(fg)(4)=f(4)g(4)=4cdot6=24$
So, $fg=left{left(-4,8 right),left(-2,4 right),left(1,6 right),left(4,24 right) right}$.
Here, $textbf{we add the values of the dependent variable for identical
values of the independent variable}$ of functions $f$ and $g$, and on the following picture is graph of function $f+g$:
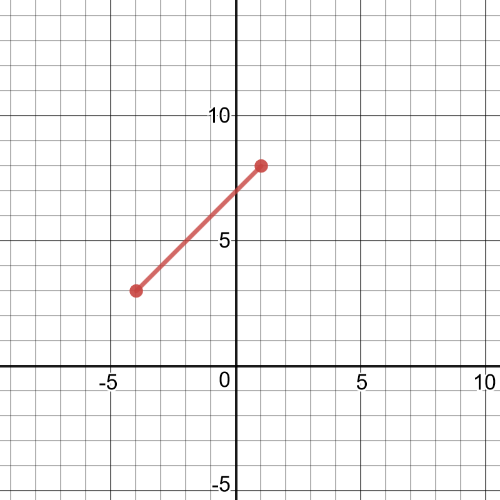
Here, $textbf{we add the values of the dependent variable for identical
values of the independent variable}$ of functions $f$ and $g$, and on the following picture is graph of function $f+g$:
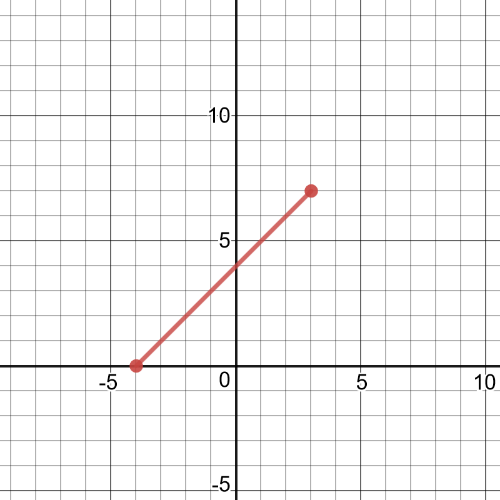
Here, $textbf{we subtract the values of the dependent variable for identical
values of the independent variable}$ of functions $f$ and $g$ and on following picture we have graph of function $f-g$:
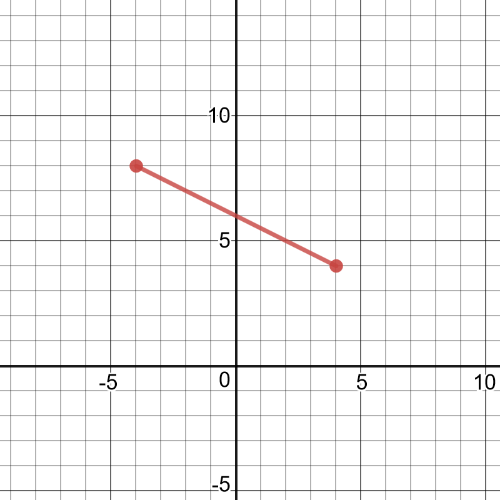
Here, $textbf{we subtract the values of the dependent variable for identical
values of the independent variable}$ of functions $f$ and $g$, but on shared domain which is $left[-4,3 right]$ and on following picture we have graph of function $f-g$:
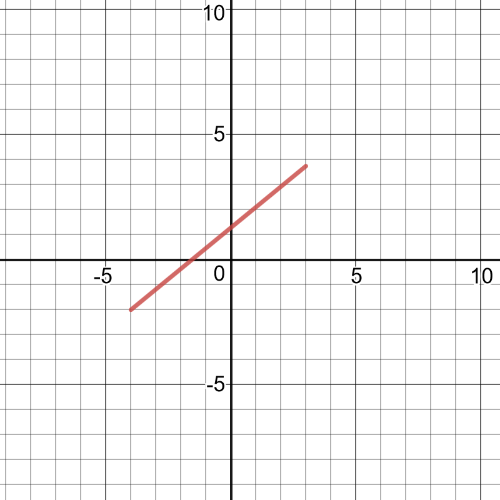
Here, $textbf{we multiply the values of the dependent variable for identical
values of the independent variable}$ of functions $f$ and $g$, and on the following picture is graph of function $fg$:
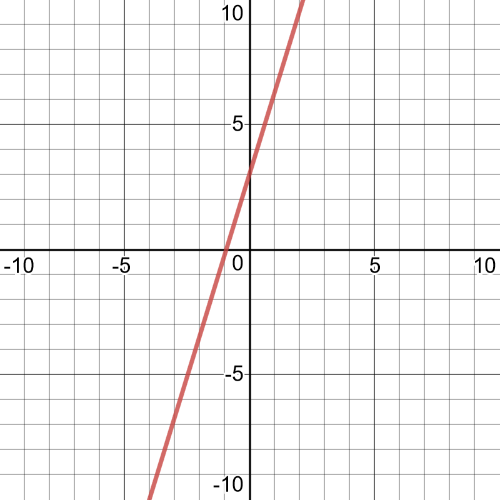
Here, $textbf{we multiply the values of the dependent variable for identical
values of the independent variable}$ of functions $f$ and $g$, and on the following picture is graph of function $fg$:
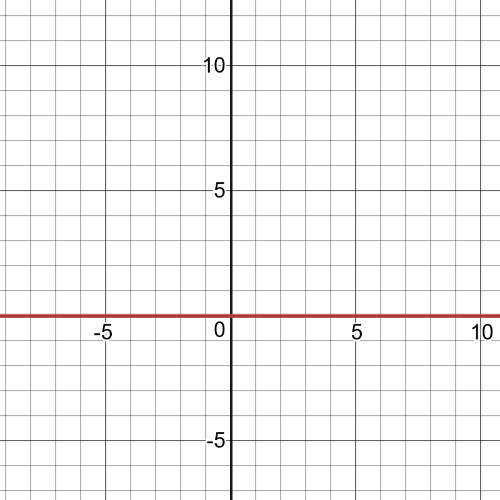
Here we have that our function is:
$h(x)=f(x)+g(x)=x^2+(-x^2)=x^2-x^2=0$
$textbf{And its graph is on the following picture:}$
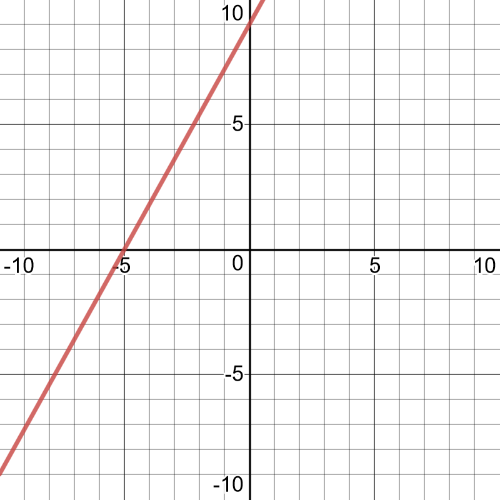
Here we have that our function is:
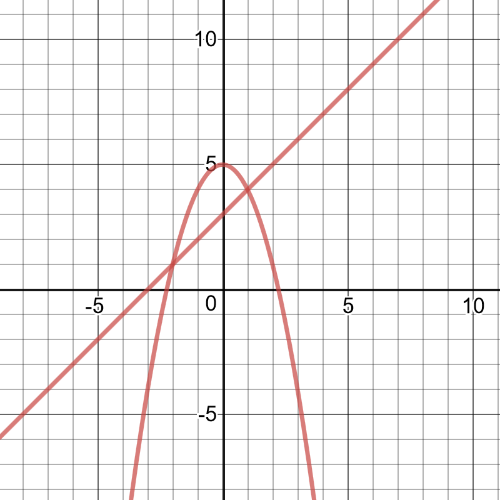
$p(x)=m(x)-n(x)=x^2-(-7x+12)=x^2+7x-12$
$textbf{And its graph is on the following picture:}$
Here we have that our function is:
$r(x)=s(x)+t(x)=left|x right|+2^x$
$textbf{And its graph is on the following picture:}$
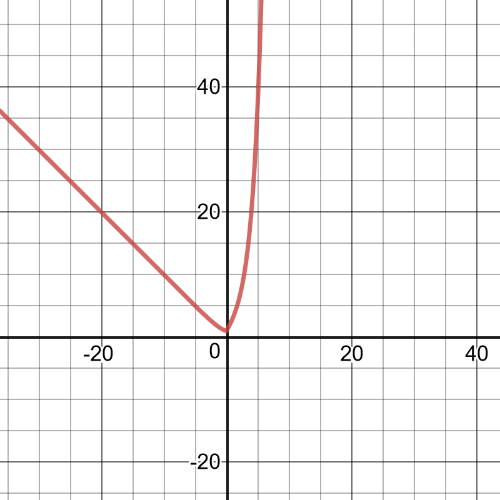
Here we have that our function is:
$a(x)=b(x)cdot{c(x)}=xcdot{x^2}=x^3$
$textbf{And its graph is on the following picture:}$
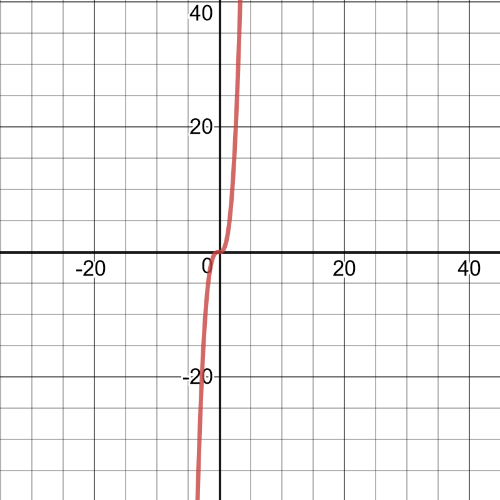
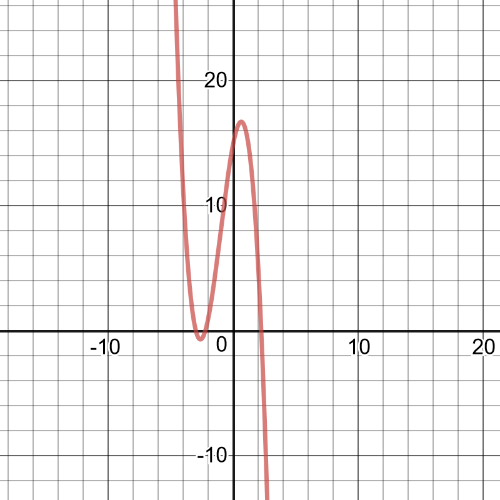
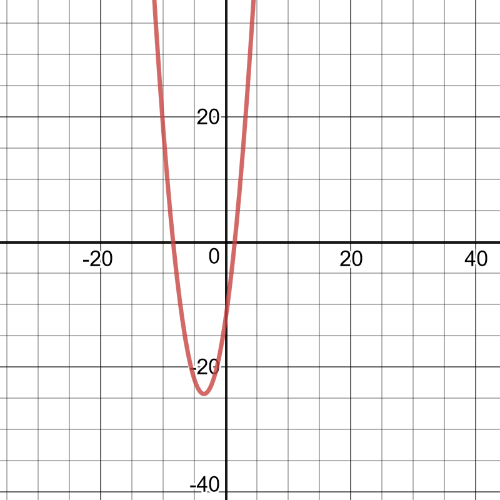
$h(x)=(x+5)(-x^2+5)=-x^3-3x^2+5x+15$
We can conclude that $textbf{degree}$ is $3$.
#### (e)
$D=Bbb{R}$, $textbf{it is the same as the domain of }f$ and $g$.
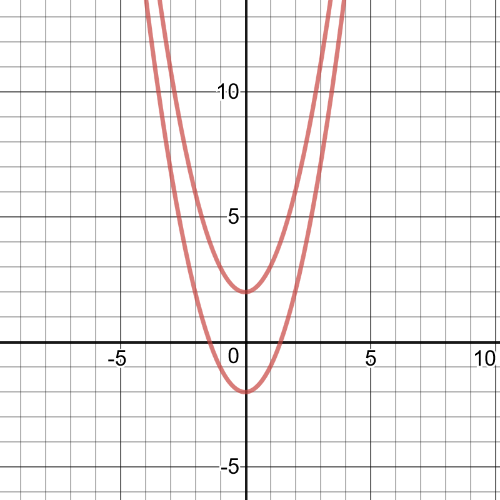
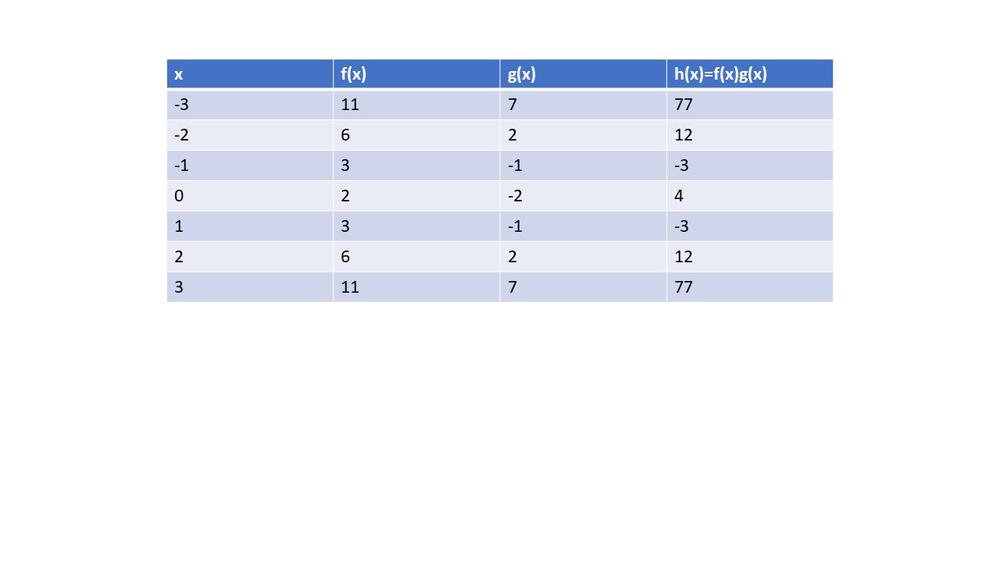
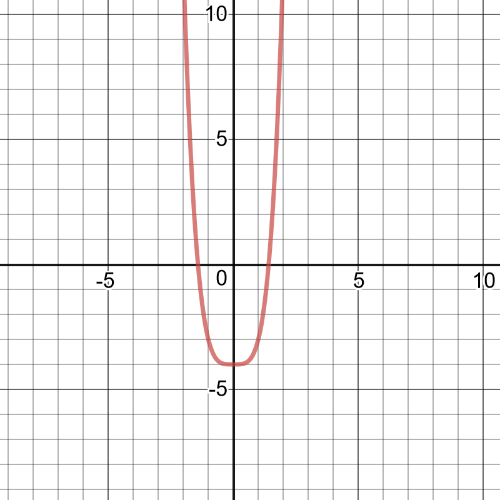
$h(x)=(x^2+2)(x^2-2)=x^2-4$
So, we can conclude that $textbf{degree}$ is $4$.
#### (e)
$D=Bbb{R}$.

