
All Solutions
Page 544: Practice Questions
$(f+g)(x)=left{(-9, -2+4), (-6, -3+ – 6), (0,2+12) right}$
$=left{(-9, 2), (-6, -9), (0,14) right}$
#### (b)
$(g+f)(x)=left{-9,4+ -2), (-6, -6+-3), (0,12+2) right}$
$=left{(-9,2), (-6, -9), (0, 14) right}$
#### (c)
$(f-g)(x)=left{(-9, -2-4), (-6, -3- -6), (0,2-12) right}$
$=left{(-9, -6), (-6,3), (0, -10) right}$
#### (d)
$(g-f)(x)=left{(-9,4- -2), (-6, -6- -3), (0,12-2) right}$
$=left{(-9,6), (-6, -3), (0, 10) right}$
$$
P(x)=R(x)-C(x)=-5x^2+150x-(10x+30)=-5x^2+140x-30
$$
#### (b)
On the following picture there is a graph of $textbf{revenue, cost and profit}$, where revenue is red, cost is purple and profit is green.
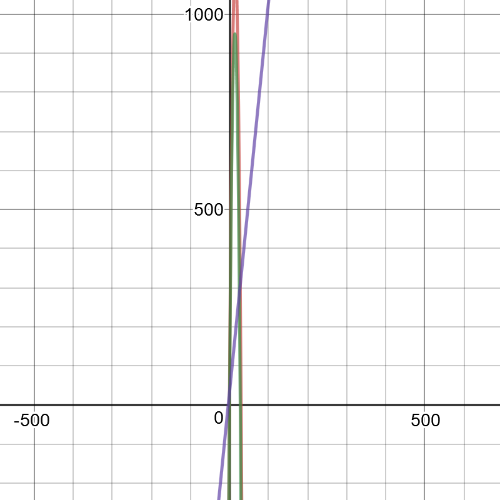
$textbf{Profit}$ = $-5(7.5)^2+140(7.5)-30=738.75$
$$
$ thousand $=738750 $
$$
$.
$R(h)=24.39 h$
#### (b)
$N(h)=24.97h$
#### (c)
$W(h)=24.78h$
#### (d)
$S(h)=24.39h+0.58h+0.39h=25.36h$
#### (e)
$25.36(8)+1.5(25.36)(3)=$317$
$(ftimes g)(x)=left(x+dfrac{1}{2} right)left(x+dfrac{1}{2} right)=x^2+x+dfrac{1}{4}$
$D=left{xinBbb{R} right}$
#### (b)
$(ftimes g)(x)=sin(3x)(sqrt{x-10})$
$D=left{xinBbb{R}|xgeq 10 right}$
#### (c)
$(ftimes g)(x)=11x^3 times dfrac{2}{x+5}=dfrac{22x^3}{x+5}$
$D=left{xinBbb{R}|xne -5 right}$
#### (d)
$(ftimes g)(x)=(90x-1)(90x+1)=8100x^2-1$
$D=left{xinBbb{R} right}$
$$begin{aligned}
R(h)&=C(h) times D(h)\
&=90cosleft(dfrac{pi}{6}cdot hright)sinleft(dfrac{pi}{6} cdot hright)-102sinleft(dfrac{pi}{6}cdot hright)\
&phantom{=}-210cosleft(dfrac{pi}{6}cdot hright)+238\
end{aligned}$$
Here we have **graph** of function from part (a):
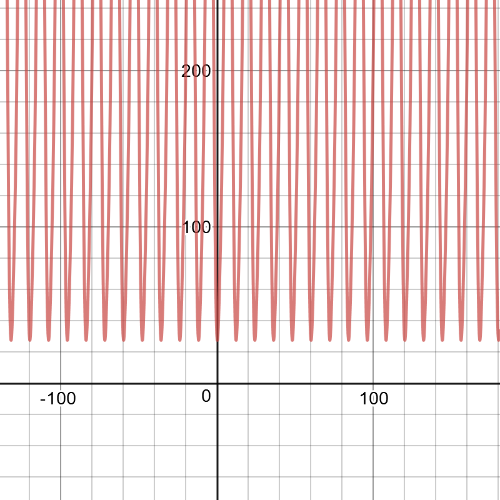
$$begin{aligned}
R(2)&=90cosleft(dfrac{pi}{6}cdot 2right)sinleft(dfrac{pi}{6} cdot 2right)-102sinleft(dfrac{pi}{6}cdot 2right)\
&phantom{=}-210cosleft(dfrac{pi}{6}cdot2right)+238\
&=470.30
end{aligned}$$
$(f div g)(x)=240div3x=dfrac{80}{x}$
$D=left{xinBbb{R}|xne 0 right}$
#### (b)
$(fdiv g)(x)=dfrac{10x^2}{x^3-3x}=dfrac{10x^2}{x(x^2-3)}=dfrac{10x^2}{x^2-3}$
$D=left{xinBbb{R}|xne pm sqrt{3} right}$
#### (c)
$(fdiv g)(x)=dfrac{x+8}{sqrt{x-8}}$
$D=left{xinBbb{R}|x > 8 right}$
#### (d)
$(fdiv g)(x)=dfrac{7x^2}{log x}$
$D=left{xinBbb{R}|x>0 right}$
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

