$(f div g)(x)=dfrac{5}{x}, xne0$

#### (b)

$(f div g)(x)=dfrac{4x}{2x-1}, xnedfrac{1}{2}$

#### (c)

$(fdiv g)(x)=dfrac{4x}{x^2+4}$

#### (d)

$(fdiv g)(x)=dfrac{(x+2)(sqrt{x-2})}{x-2}, x>2$

#### (e)

$(fdiv g)(x)=dfrac{8}{1+left(dfrac{1}{2} right)^x}$

#### (f)

$(fdiv g)(x)=dfrac{x^2}{log(x)}, x>0$

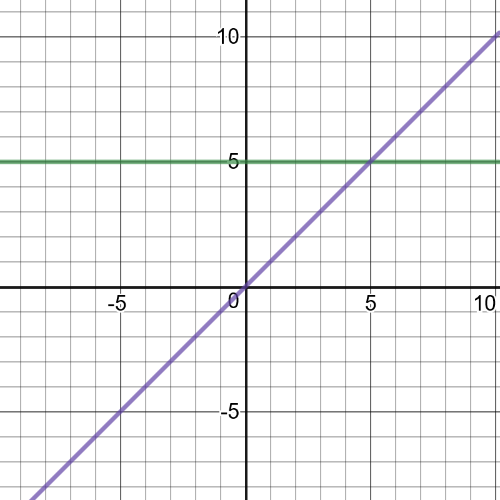
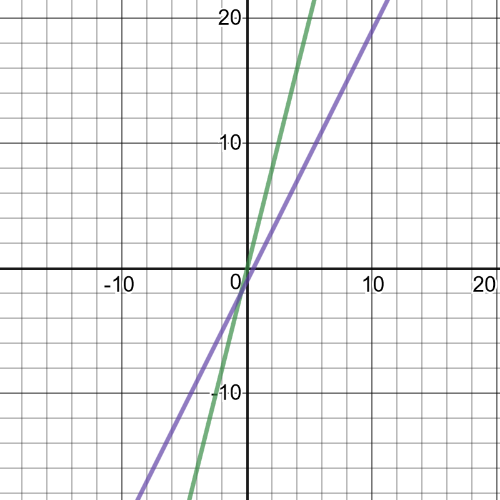
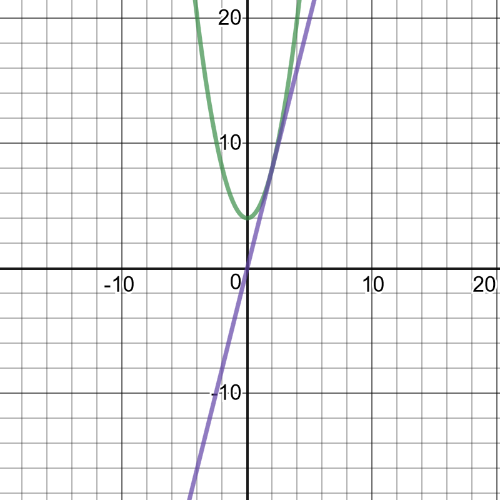
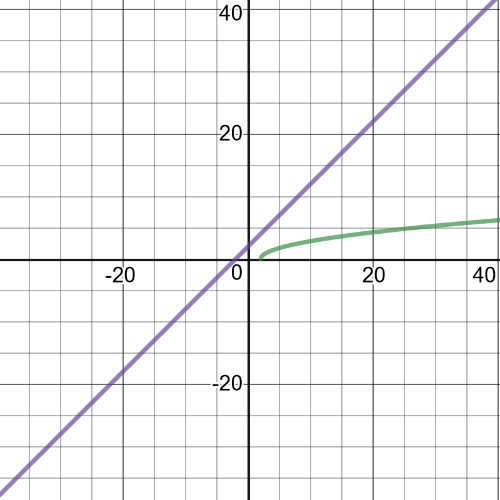
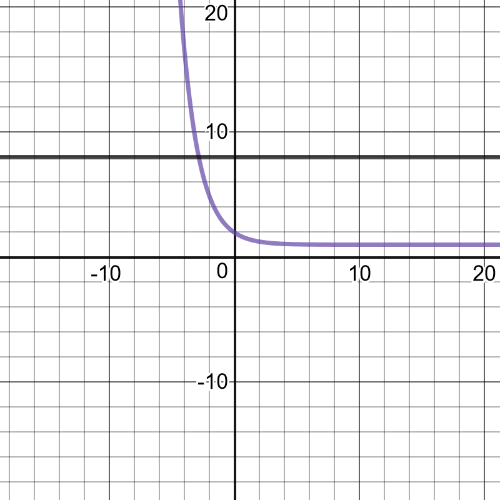
1(a): domain of $f: left{xinBbb{R} right}$; domain of $g: left{xinBbb{R} right}$

1(b): domain of $f: left{xinBbb{R} right}$; domain of $g: left{xinBbb{R} right}$

1(c): domain of $f: left{xinBbb{R} right}$; domain of $g: left{xinBbb{R} right}$

1(d): domain of $f: left{xinBbb{R} right}$; domain of $g:left{ xinBbb{R}|xgeq 2right}$

1(e): domain of $f: left{xinBbb{R} right}$; domain of $g: left{xinBbb{R} right}$

1(f): domain of $f: left{xinBbb{R} right}$; domain of $g:left{xinBbb{R}|x > 0 right}$

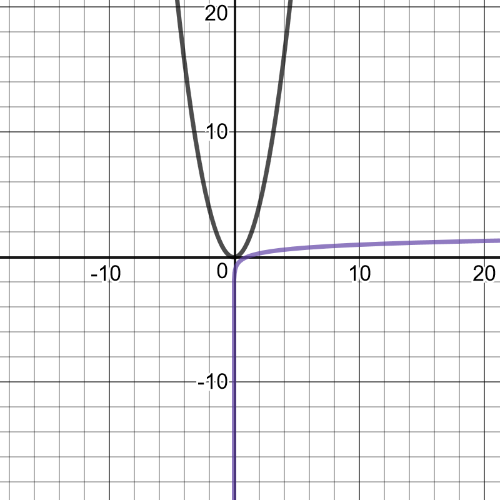
1(a): domain of $(fdiv g): left{xinBbb{R}|xne 0 right}$

1(b): domain of $(fdiv g): left{ xinBbb{R}|xne dfrac{1}{2}right}$

1(c): domain of $(fdiv g): left{xinBbb{R} right}$

1(d): domain of $(fdiv g): left{xinBbb{R}|x > 2 right}$

1(e): domain of $(fdiv g): left{xinBbb{R} right}$

1(f): domain of $(fdiv g): left{xin Bbb{R}|x > 0 right}$

$dfrac{260}{1+24(0.9)^t}=dfrac{260}{1+24(0.9)^{20}}=66$cm

textbf{The rate of change is $left[66-(260 div 25) right] div 20$ or $2.798$ cm/day.
}

#### (b)

The maximum height is $260$, so half of $260$ is $130$ cm.

$130=dfrac{260}{1+24(0.9)^t}$

$130+3120(0.9)^t=260$

$3120(0.9)^t=130$

$(0.9)^t=130 div 3120$

$tlog0.9=log(130 div 3120)$

$t=30$ days

#### (c)

$left(dfrac{260}{1+24(0.9)^{30.1}}-dfrac{260}{1+24 (0.9)^{30}} right)div 0.1= 6.848$ cm/day

#### (d)

It slows down and eventually comes to zero.This is seen on the graph as it becomes horizontal at the top.