Express in logarithmic form for the following expression.

$$
color{#4257b2}(a) y=5^x
$$

According the following form:

$$
because y=a^x therefore y=log_a(x) text{So}
$$

$$
y=5^x y=log_5(x)
$$

$$
color{#4257b2}(b) y=left(dfrac{1}{3}right)^x
$$

According the following form:

$$
because y=a^x therefore y=log_a(x) text{So}
$$

$$
y=left(dfrac{1}{3}right)^x y=log_{tfrac{1}{3}}(x)
$$

$$
color{#4257b2}(c) x=10^y
$$

According the following form:

$$
because y=a^x therefore y=log_a(x) text{So}
$$

$$
x=10^y x=log_{10}(y)
$$

$$
color{#4257b2}(d) m=p^q
$$

According the following form:

$$
because y=a^x therefore y=log_a(x) text{So}
$$

$$
m=p^q m=log_p(q)
$$

$text{$text{color{#c34632}(a) $y=log_5(x)$ (b) $y=log_{tfrac{1}{3}}(x)$
\ \
(c) $ x=log_{10}(y)$ (d) $ m=log_p(q)$
\}$}$

Express in exponential form for the following expression.

$$
color{#4257b2}text{(a)} y=log_3(x)
$$

According the following form:

$$
because y=log_a(x) therefore y=a^x text{So}
$$

$$
y=log_3(x) y=3^x
$$

$$
color{#4257b2}text{(b)} y=log(x)
$$

According the following form:

$$
log(x)=log_{10}(x)
$$

$$
because y=log_a(x) therefore y=a^x text{So}
$$

$$
y=log(x) y=log_{10}(x) y=10^x
$$

$$
color{#4257b2}text{(c)} k=log(m)
$$

According the following form:

$$
log(x)=log_{10}(x)
$$

$$
because y=log_a(x) therefore y=a^x text{So}
$$

$$
k=log(m) k=log_{10}(m) y=10^m
$$

$$
color{#4257b2}text{(d)} t=log_5(r)
$$

According the following form:

$$
because y=log_a(x) therefore y=a^x text{So}
$$

$$
t=log_5(r) t=5^r
$$

$text{$text{color{#c34632}(a) $y=3^x$ (b) $y=10^x$
\ \
(c) $y=10^m$ (d) $t=5^r$
\}$}$

Describe the transformation for the following function.

$$
color{#4257b2}text{(a)} f(x)=2log(x)-4
$$

$$
a=2 k=1 c=-4
$$

$$
color{#4257b2}text{(b)} f(x)=-log(3x)
$$

$$
a=-1 k=3
$$

$$
color{#4257b2}text{(c)} f(x)=dfrac{1}{4}logleft(dfrac{1}{4}xright)
$$

$$
a=dfrac{1}{4} k=dfrac{1}{4}
$$

$$
color{#4257b2}text{(d)} f(x)=log[2(x-2)]
$$

$$
k=2 d=2
$$

$$
color{#4257b2}text{(e)} f(x)=log(x+5)+1
$$

$$
d=-5 c=1
$$

$$
color{#4257b2}text{(f)} f(x)=5log(-x)-3
$$

$$
a=2 k=-1 c=-3
$$

$$
text{color{#c34632}(a) $a=2 k=1 c=-4$
\ \
(b) $a=-1 k=3$
\ \
(c) $a=dfrac{1}{4} k=dfrac{1}{4}$
\ \
(d) $k=2 d=2$
\ \
(e) $d=-5 c=1$
\ \
(f) $a=2 k=-1 c=-3$}
$$

Write the equation of the function that resulted from the each of the following transformation.

$$
color{Brown}text{Note that: parent function is} y=log_3(x)
$$

$$
color{#4257b2}text{(a)} a=4 k=-1
$$

$$
y=4log_3(-x)
$$

$$
color{#4257b2}text{(b)} d=-3 c=1
$$

$$
y=log_3(x+3)+1
$$

$$
color{#4257b2}text{(c)} a=dfrac{2}{3} k=dfrac{1}{2}
$$

$$
y=dfrac{2}{3}log_3left(dfrac{1}{2}xright)
$$

$$
color{#4257b2}text{(d)} a=3 k=-1 d=1
$$

$$
y=3log_3(-x-1)
$$

$$
text{color{#c34632}(a) $y=4log_3(-x)$ (b) $y=log_3(x+3)+1$
\ \
(c) $y=dfrac{2}{3}log_3left(dfrac{1}{2}xright)$ (d) $y=3log_3(-x-1)$}
$$

State the coordinate of the point $(9, 2)$ for each of the transformed function in question $4$.

$$
color{#4257b2}text{(a)} y=4log_3(-x)
$$

Multiply the coordinate of $x$ points by $(-1)$ and $y$ points by $(4)$ as follows

$(x, y)rightarrow(-x, 4y)$:

$$
(9, 2)rightarrow(-9, 8)
$$

$$
color{#4257b2}text{(b)} y=log_3(x+3)+1
$$

Adding to the coordinate of $x$ points by $(-3)$ and $y$ points by $(1)$ as follows

$(x, y)rightarrow(x-3, y+1)$:

$$
(9, 2)rightarrow(6, 3)
$$

$$
color{#4257b2}text{(c)} y=dfrac{2}{3}log_3left(dfrac{1}{2}xright)
$$

Multiply the coordinate of $x$ points by $left(dfrac{1}{2}right)$ and $y$ points by $left(dfrac{2}{3}right)$ as follows

$(x, y)rightarrowleft(dfrac{1}{2}x, dfrac{2}{3}yright)$:

$$
(9, 2)rightarrowleft(dfrac{9}{2}, dfrac{4}{3}right)
$$

$$
color{#4257b2}text{(d)} y=3log_3(-x-1)
$$

Multiply the coordinate of $x$ points by $(-1)$ and $y$ points by $(3)$ as follows

$(x, y)rightarrow(-x, 3y)$:

$$
(9, 2)rightarrow(-9, 6)
$$

Adding to the coordinate of $x$ points by $(1)$ as follows

$(-x, 3y)rightarrow(-x+1, 3y)$:

$$
(-9, 6)rightarrow(-8, 6)
$$

$$
text{color{#c34632}(a) $(-9, 8)$ (b) $(6, 3)$
\ \
(c) $left(dfrac{9}{2}, dfrac{4}{3}right)$ (d) $(-8, 6)$}
$$

How does the graph of $f(x)=2log_2(x)+2$ with graph of $g(x)=log_2(x)$

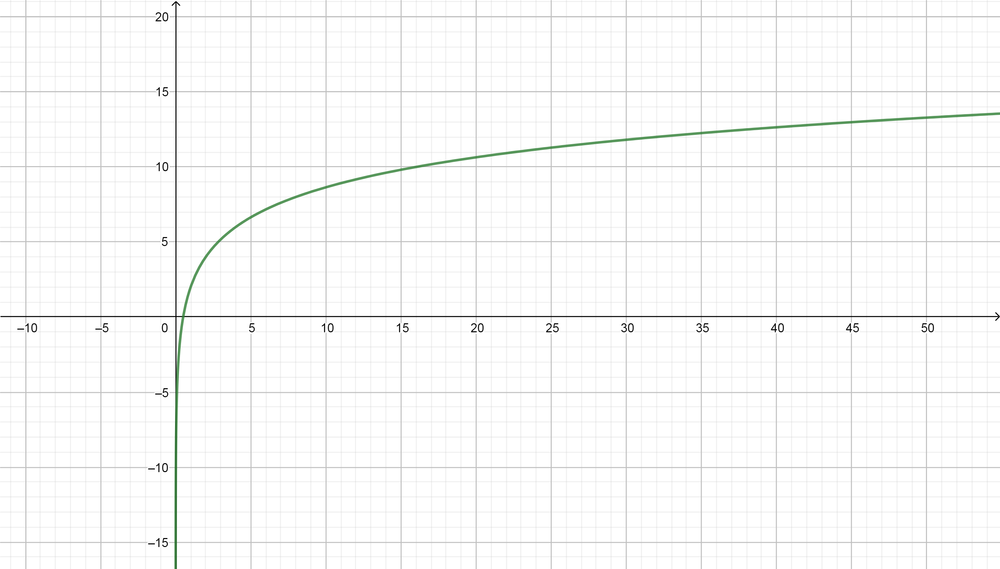
$$
text{color{#4257b2}For the graph of $f(x)=2log_2(x)+2$}
$$

Domain$=(0, infty)$, Range$=(-infty, infty)$, Symptote equation$ (x=0)$

$$
text{color{#4257b2}For the graph of $g(x)=log_2(x)$}
$$

Domain$=(0, infty)$, Range$=(-infty, infty)$, Symptote equation$ (x=0)$

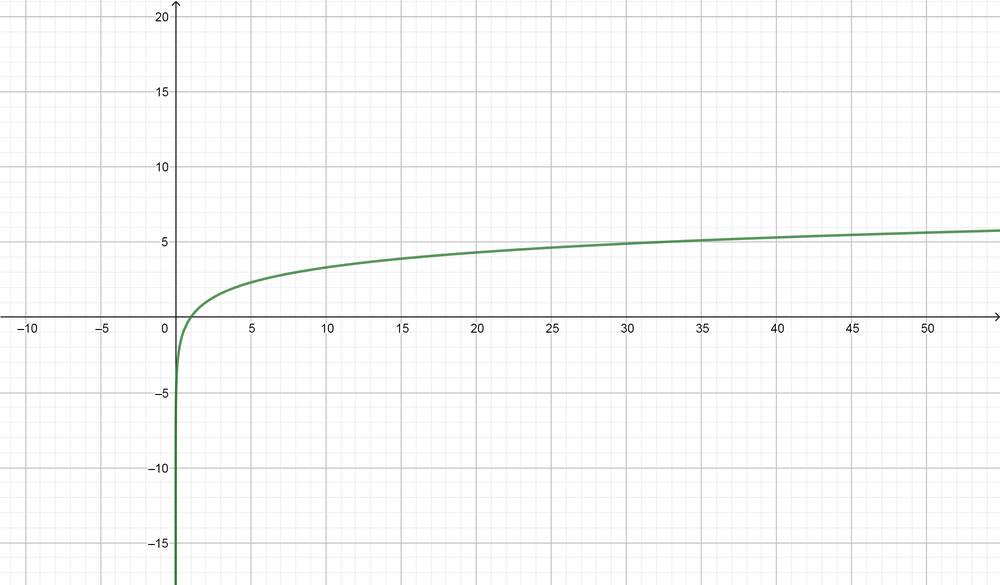
$$
text{color{#c34632}Domain$=(0, infty)$, Range$=(-infty, infty)$, Symptote equation$ (x=0)$}
$$

Evaluate the following expression.

$$
color{#4257b2}text{(a)} log_3(81)
$$

To evaluate the expression, write it in the exponential form to which $(3)$ must be raised to get $(81)$ as follows:

$$
3^x=81
$$

Rewrite $(81)$ as a power of $(3)$ as follows:

$$
3^x=3^4 x=4
$$

$$
log_3(81)=4
$$

$$
color{#4257b2}text{(b)} log_4left(dfrac{1}{16}right)
$$

To evaluate the expression, write it in the exponential form to which $(4)$ must be raised to get $left(tfrac{1}{16}right)$ as follows:

$$
4^x=dfrac{1}{16}
$$

Rewrite $left(tfrac{1}{16}right)$ as a power of $(4)$ as follows:

$$
4^x=left(dfrac{1}{4}right)^2 4^x=4^{-2} x=-2
$$

$$
log_4left(dfrac{1}{16}right)=-2
$$

$$
color{#4257b2}text{(c)} log_5(1)
$$

To evaluate the expression, write it in the exponential form to which $(5)$ must be raised to get $(1)$ as follows:

$$
5^x=1
$$

Rewrite $(1)$ as a power of $(5)$ as follows:

$$
5^x=5^0 x=0
$$

$$
log_5(1)=0
$$

$$
color{#4257b2}text{(d)} log_{tfrac{2}{3}}left(dfrac{27}{8}right)
$$

To evaluate the expression, write it in the exponential form to which $left(frac{2}{3}right)$ must be raised to get $left(frac{27}{8}right)$ as follows:

$$
left(dfrac{2}{3}right)^x=dfrac{27}{8}
$$

Rewrite $left(frac{27}{8}right)$ as a power of $left(frac{2}{3}right)$ as follows:

$$
left(dfrac{2}{3}right)^x=left(dfrac{3}{2}right)^3
$$

$$
left(dfrac{2}{3}right)^x=left(dfrac{2}{3}right)^{-3} x=-3
$$

$$
log_{tfrac{2}{3}}left(dfrac{27}{8}right)=-3
$$

$$
text{color{#c34632}(a) $log_3(81)=4$ (b) $log_4left(dfrac{1}{16}right)=-2$
\ \ \
(c) $log_5(1)=0$ (d) $log_{tfrac{2}{3}}left(dfrac{27}{8}right)=-3$}
$$

We would like to evaluate the following expressions.

$$
color{#4257b2}text{(a)} log(4)
$$

According to the following forms.

$$
log(x)=log_{10}(x) log_a(b)=dfrac{log(b)}{log(a)}
$$

$$
therefore log(4)=log_{10}(4)=dfrac{log(4)}{log(10)}
$$

$$
therefore log(4)=dfrac{0.602}{1}=0.602
$$

$$
color{#4257b2}text{(b)} log(45)
$$

According to the following forms.

$$
log(x)=log_{10}(x) log_a(b)=dfrac{log(b)}{log(a)}
$$

$$
therefore log(45)=log_{10}(45)=dfrac{log(45)}{log(10)}
$$

$$
therefore log(45)=dfrac{1.653}{1}=1.653
$$

$$
color{#4257b2}text{(c)} log(135)
$$

According to the following forms.

$$
log(x)=log_{10}(x) log_a(b)=dfrac{log(b)}{log(a)}
$$

$$
therefore log(135)=log_{10}(135)=dfrac{log(135)}{log(10)}
$$

$$
therefore log(135)=dfrac{2.130}{1}=2.130
$$

$$
color{#4257b2}text{(d)} log(300)
$$

According to the following forms.

$$
log(x)=log_{10}(x) log_a(b)=dfrac{log(b)}{log(a)}
$$

$$
therefore log(300)=log_{10}(300)=dfrac{log(300)}{log(10)}
$$

$$
therefore log(300)=dfrac{2.477}{1}=2.477
$$

$$
text{color{#c34632}(a) $log(4)=0.602$ (b) $log(45)=1.653$
\ \
(c) $log(135)=2.130$ (d) $log(300)=2.477$}
$$

We would like to evaluate the following expressions.

$$
color{#4257b2}text{(a)} log_2(21)
$$

According to the following form $left[log_a(b)=dfrac{log(b)}{log(a)}right].$

$$
therefore log_2(21)=dfrac{log(21)}{log(2)}
$$

$$
therefore log_2(21)=dfrac{1.322}{0.301}=4.392
$$

$$
color{#4257b2}text{(b)} log_5(117)
$$

According to the following form $left[log_a(b)=dfrac{log(b)}{log(a)}right].$

$$
therefore log_5(117)=dfrac{log(117)}{log(5)}
$$

$$
therefore log_5(117)=dfrac{2.068}{0.698}=2.963
$$

$$
color{#4257b2}text{(c)} log_7(141)
$$

According to the following form$left[log_a(b)=dfrac{log(b)}{log(a)}right].$

$$
therefore log_7(141)=dfrac{log(141)}{log(7)}
$$

$$
therefore log_7(141)=dfrac{2.149}{0.845}=2.543
$$

$$
color{#4257b2}text{(d)} log_{11}(356)
$$

According to the following form$left[log_a(b)=dfrac{log(b)}{log(a)}right].$

$$
therefore log_{11}(356)=dfrac{log(356)}{log(11)}
$$

$$
therefore log_{11}(356)=dfrac{2.551}{1.041}=2.451
$$

$$
text{color{#c34632}(a) $log_2(21)=4.392$ (b) $log_5(117)=2.963$
\ \
(c) $log_7(141)=2.543$ (d) $log_{11}(356)=2.451$}
$$

(a) We would like to write the expression $color{#4257b2}log 7+log 4$ as a single logarithm. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log 7+log 4&=log left[left(7right)cdot left(4right)right]
\ \
&=log 28
end{align*}
$$

So the expression $color{#4257b2}log 7+log 4$ can be simplified to the single logarithm $boxed{ log 28 }$

(b) We would like to write the expression $color{#4257b2}log 5-log 2$ as a single logarithm. First, we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log 5-log 2&=log left(dfrac{5}{2}right)
\ \
&=log 2.5
end{align*}
$$

So the expression $color{#4257b2}log 5-log 2$ can be simplified to the single logarithm $boxed{ log 2.5 }$

(c) We would like to write the expression $color{#4257b2}log_{3} 11+log_{3} 4 – log_{3} 6$ as a single logarithm. First, we note that the first two terms in our expression is a sum of logarithms, so we can use the product law of logarithms where
$color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{3} 11+log_{3} 4 – log_{3} 6&=left(log_{3} 11+log_{3} 4right) – log_{3} 6
\ \
&=log_{3}left[(11)cdot (4)right]-log_{3} 6
\ \
&=log_{3} 44-log_{3} 6
end{align*}
$$

Now we note that our expression is simplified to a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{3} 11+log_{3} 4 – log_{3} 6&=log_{3} 44-log_{3} 6
\ \
&=log_{3}left(dfrac{44}{6}right)
\ \
&=log_{3} left(dfrac{22}{3}right)
end{align*}
$$

So the expression $color{#4257b2}log_{3} 11+log_{3} 4 – log_{3} 6$ can be simplified to the single logarithm $boxed{ log_{3} left(dfrac{22}{3}right) }$

(d) We would like to write the expression $color{#4257b2}log_{p} q+log_{p} q$ as a single logarithm. First, we note that our expression is a sum between two logarithms have the same base and the same number inside the logarithm, so we can sum them directly.

$$
log_{p} q+log_{p} q=2log_{p} q
$$

So the expression $color{#4257b2}log_{p} q+log_{p} q$ can be simplified to the single logarithm $boxed{ 2log_{p} q }$

Large{$text{$text{color{#c34632}(a) $log 28$ (c) $log_{3} left(dfrac{22}{3}right)$
\
\
Large{color{#c34632}(b) $ log 2.5$ (d) $2log_{p} q$}$}$

(a) We would like to evaluate $color{#4257b2}log_{11} 33-log_{11} 3$. First, we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{11} 33-log_{11} 3&=log_{11} left(dfrac{33}{3}right)
\ \
&=log_{11} 11
end{align*}
$$

But we know from the property of logarithm that $color{#4257b2}log_{a} a=1$, so we can replace $color{#4257b2}log_{11} 11$ by $color{#4257b2}1$.

$$
begin{align*}
log_{11} 33-log_{11} 3&=log_{11} 11
\ \
&=1
end{align*}
$$

So the expression $color{#4257b2}log_{11} 33-log_{11} 3$ equals $boxed{ 1 }$

(b) We would like to evaluate $color{#4257b2}log_{7} 14+log_{7} 3.5$. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{7} 14+log_{7} 3.5&=log_{7} left[left(14right)cdot left(3.5right)right]
\ \
&=log_{7} 49
end{align*}
$$

But we know that $color{#4257b2}49=7^{2}$, so we can replace $color{#4257b2}49$ from our expression by $color{#4257b2}7^{2}$.

$$
begin{align*}
log_{7} 14+log_{7} 3.5&=log_{7} 49
\ \
&=log_{7} 7^{2}
end{align*}
$$

Now we note that our expression is simplified to $color{#4257b2}log_{7} 7^{2}$ which is on the form of the power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
begin{align*}
log_{7} 14+log_{7} 3.5&=log_{7} 7^{2}
\ \
&=2 log_{7} 7
\ \
&=(2)cdot (1)=2
end{align*}
$$

Note that in the final step we used the property of logarithm that $color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{7} 14+log_{7} 3.5$ equals $boxed{ 2 }$

(c) We would like to evaluate $color{#4257b2}log_{5} 100+log_{5} dfrac{1}{4}$. First, we note that our expression is a sum of logarithms, so we can use the product law of logarithms where $color{#4257b2}log_{a} x+log_{a} y=log_{a} xy$.

$$
begin{align*}
log_{5} 100+log_{5} dfrac{1}{4}&=log_{5} left[left(100right)cdot left(dfrac{1}{4}right)right]
\ \
&=log_{5} 25
end{align*}
$$

But we know that $color{#4257b2}25=5^{2}$, so we can replace $color{#4257b2}25$ from our expression by $color{#4257b2}5^{2}$.

$$
begin{align*}
log_{5} 100+log_{5} dfrac{1}{4}&=log_{5} 25
\ \
&=log_{5} 5^{2}
end{align*}
$$

Now we note that our expression is simplified to $color{#4257b2}log_{5} 5^{2}$ which is on the form of the power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
begin{align*}
log_{5} 100+log_{5} dfrac{1}{4}&=log_{5} 5^{2}
\ \
&=2 log_{5} 5
\ \
&=(2)cdot (1)=2
end{align*}
$$

Note that in the final step we used the property of logarithm that $color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{5} 100+log_{5} dfrac{1}{4}$ equals $boxed{ 2 }$

(d) We would like to evaluate $color{#4257b2}log_{frac{1}{2}} 72-log_{frac{1}{2}} 9$. First, we note that our expression is a difference of logarithms, so we can use the quotient law of logarithms where $color{#4257b2}log_{a} x-log_{a} y=log_{a} left(dfrac{x}{y}right)$.

$$
begin{align*}
log_{frac{1}{2}} 72-log_{frac{1}{2}} 9&=log_{frac{1}{2}} left(dfrac{72}{9}right)
\ \
&=log_{frac{1}{2}} 8
end{align*}
$$

But we know that $color{#4257b2}8=2^{3}$, so we can replace $color{#4257b2}8$ from our expression by $color{#4257b2}2^{3}$.

$$
begin{align*}
log_{frac{1}{2}} 72-log_{frac{1}{2}} 9&=log_{frac{1}{2}} 8
\ \
&=log_{frac{1}{2}} 2^{3}
end{align*}
$$

Now we can use the exponent property $color{#4257b2}x^{a}=dfrac{1}{(x)^{-a}}$ to replace $color{#4257b2}2^{3}$ by $color{#4257b2}dfrac{1}{(2)^{-3}}$.

$$
begin{align*}
log_{frac{1}{2}} 72-log_{frac{1}{2}} 9&=log_{frac{1}{2}} 2^{3}
\ \
&=log_{frac{1}{2}} dfrac{1}{(2)^{-3}}
\ \
&=log_{frac{1}{2}} dfrac{(1)^{-3}}{(2)^{-3}}
\ \
&=log_{frac{1}{2}} left(dfrac{1}{2}right)^{-3}
end{align*}
$$

Note that we used the fact $color{#4257b2}(1)^{x}=1$ to replace $color{#4257b2}1$ by $color{#4257b2}1^{-3}$ to make the numerator and denominator have the same exponent. Now we note that our expression is simplified to $color{#4257b2}log_{frac{1}{2}}left(dfrac{1}{2}right)^{-3}$ which is on the form of the power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
begin{align*}
log_{frac{1}{2}} 72-log_{frac{1}{2}} 9&=log_{frac{1}{2}} left(dfrac{1}{2}right)^{-3}
\ \
&=(-3)cdot log_{frac{1}{2}} left(dfrac{1}{2}right)
\ \
&=(-3)cdot (1)=-3
end{align*}
$$

Note that in the final step we used the property of logarithm that $color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{frac{1}{2}} 72-log_{frac{1}{2}} 9$ equals $boxed{ -3 }$

(e) We would like to evaluate $color{#4257b2}log_{4} sqrt[3]{16}$. First, we know that $color{#4257b2}16=4^{2}$, so we can replace $color{#4257b2}16$ from our expression by $color{#4257b2}4^{2}$

$$
log_{4} sqrt[3]{16}=log_{4} sqrt[3]{4^{2}}
$$

But we know that $color{#4257b2}sqrt[a]{x^{b}}=x^{frac{b}{a}}$, so we can replace $color{#4257b2}sqrt[3]{4^{2}}$ from our expression by $color{#4257b2}(4)^{frac{2}{3}}$.

$$
begin{align*}
log_{4} sqrt[3]{16}&=log_{4} sqrt[3]{4^{2}}
\ \
&=log_{4} (4)^{frac{2}{3}}
end{align*}
$$

Now we note that our expression is simplified to $color{#4257b2}log_{4} (4)^{frac{2}{3}}$ which is on the form of the power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
begin{align*}
log_{4} sqrt[3]{16}&=log_{4} (4)^{frac{2}{3}}
\ \
&=dfrac{2}{3} log_{4} 4
\ \
&=left(dfrac{2}{3}right)cdot (1)
\ \
&=dfrac{2}{3}
end{align*}
$$

Note that in the final step we used the property of logarithm that $color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{4} sqrt[3]{16}$ equals $boxed{ dfrac{2}{3} }$

(f) We would like to evaluate $color{#4257b2}log_{3} 9 sqrt{27}$. First, we know that $color{#4257b2}9=3^{2}$ and $color{#4257b2}27=3^{3}$, so we can replace $color{#4257b2}9$ and $color{#4257b2}27$ from our expression by $color{#4257b2}3^{2}$ and $color{#4257b2}3^{3}$ respectively.

$$
log_{3} 9 sqrt{27}=log_{3} left(3^{2} sqrt{3^{3}}right)
$$

But we know that $color{#4257b2}sqrt{x^{a}}=x^{frac{a}{2}}$, so we can replace $color{#4257b2}sqrt{3^{3}}$ from our expression by $color{#4257b2}(3)^{frac{3}{2}}$.

$$
begin{align*}
log_{3} 9 sqrt{27}&=log_{3} left(3^{2} sqrt{3^{3}}right)
\ \
&=log_{3} left[(3)^{2}cdot (3)^{frac{3}{2}}right]
end{align*}
$$

Now we can use the property of exponents where $color{#4257b2}x^{a}cdot x^{b}=x^{a+b}$.

$$
begin{align*}
log_{3} 9 sqrt{27}&=log_{3} left[(3)^{2}cdot (3)^{frac{3}{2}}right]
\ \
&=log_{3} (3)^{2+frac{3}{2}}
\ \
&=log_{3} (3)^{frac{7}{2}}
end{align*}
$$

Now we note that our expression is simplified to $color{#4257b2}log_{3} (3)^{frac{7}{2}}$ which is on the form of the power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{m} x^{r}=r log_{m} x$.

$$
begin{align*}
log_{3} 9 sqrt{27}&=log_{3} (3)^{frac{7}{2}}
\ \
&=dfrac{7}{2} log_{3} 3
\ \
&=left(dfrac{7}{2}right)cdot (1)=dfrac{7}{2}
end{align*}
$$

Note that in the final step we used the property of logarithm that $color{#4257b2}log_{a} a=1$.

So the expression $color{#4257b2}log_{3} 9 sqrt{27}$ equals $boxed{ dfrac{7}{2} }$

Large{$text{$text{color{#c34632}(a) $1$ (c) $2$ (e) $dfrac{2}{3}$
\
\
Large{color{#c34632}(b) $2$ (d) $-3$ (f) $dfrac{7}{2}$}$}$

We would like to describe how the graph $color{#4257b2}f(x)=log x^{3}$ is related to the graph $color{#4257b2}g(x)=log x$. First, we note that the graph $color{#4257b2}f(x)=log x^{3}$ is on the form of the power of logarithms, so we can use the property of power law of logarithms where $color{#4257b2}log_{a} m^{r}=r log_{a} m$

$$
f(x)=log x^{3}
$$

$$
f(x)=3 log x
$$

But we know that $color{#4257b2}g(x)=log x$, so we can replace $color{#4257b2}log x$ by $color{#4257b2}g(x)$ in the last equation.

$$
f(x)=3 log x
$$

$$
f(x)=3 g(x)
$$

So the relation between the two functions is $boxed{ f(x)=3 g(x)}$

$$
color{#c34632} f(x)=3g(x)
$$

(a) We would like to evaluate $color{#4257b2}log 4^{8}$. First, we note that our expression is a power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{x} m^{r}=r log_{x} m$.

$$
log 4^{8}=8 log 4
$$

Now we can use the calculator to determine $color{#4257b2}log 4$ and then multiply by $color{#4257b2}8$ to find the value of $color{#4257b2}log 4^{8}$.

$$
begin{align*}
log 4^{8}&=8 log 4
\ \
&=(8)cdot (0.6025)
\ \
&=4.82
end{align*}
$$

So the expression $color{#4257b2}log 4^{8}$ equals $boxed{ 4.82 }$

(b) We would like to evaluate $color{#4257b2}log sqrt{40}$. First, we know that $color{#4257b2}sqrt{x}=x^{frac{1}{2}}$, so we can replace $color{#4257b2}sqrt{40}$ by $color{#4257b2}(40)^{frac{1}{2}}$.

$$
log sqrt{40}=log (40)^{frac{1}{2}}
$$

Now we note that our expression is a power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{x} m^{r}=r log_{x} m$.

$$
log sqrt{40}=log (40)^{frac{1}{2}}=dfrac{1}{2} log 40
$$

Now we can use the calculator to determine $color{#4257b2}log 40$ and then multiply by $color{#4257b2}dfrac{1}{2}$ to find the value of $color{#4257b2}log sqrt{40}$.

$$
begin{align*}
log sqrt{40}&=log (40)^{frac{1}{2}}
\ \
&=dfrac{1}{2} log 40
\ \
&=left(dfrac{1}{2}right)cdot (1.602)
\ \
&=0.8
end{align*}
$$

So the expression $color{#4257b2}log sqrt{40}$ equals $boxed{ 0.8 }$

(c) We would like to evaluate $color{#4257b2}log 9^{4}$. First, we note that our expression is a power of logarithms, so we can use the power law of logarithms where $color{#4257b2}log_{x} m^{r}=r log_{x} m$.

$$
log 9^{4}=4 log 9
$$

Now we can use the calculator to determine $color{#4257b2}log 9$ and then multiply by $color{#4257b2}4$ to find the value of $color{#4257b2}log 9^{4}$.

$$
begin{align*}
log 9^{4}&=4 log 9
\ \
&=(4)cdot (0.955)
\ \
&=3.82
end{align*}
$$

So the expression $color{#4257b2}log 9^{4}$ equals $boxed{ 3.82 }$

(d) We would like to evaluate $color{#4257b2}log 200 div log 50$. First, we can use the calculator to determine $color{#4257b2}log 200$ and $color{#4257b2}log 50$ and then divide them the first result by the second result.

$$
begin{align*}
log 200 div log 50&=2.3010 div 1.69897
\ \
&=1.35
end{align*}
$$

So the expression $color{#4257b2}log 200 div log 50$ equals $boxed{ 1.35 }$

(e) We would like to evaluate $color{#4257b2}left(log 20right)^{2}$. First, we can use the calculator to determine $color{#4257b2}log 20$ and then square the result to find the value $color{#4257b2}left(log 20right)^{2}$.

$$
begin{align*}
left(log 20right)^{2}&=left(1.3010right)^{2}
\ \
&=1.69
end{align*}
$$

So the expression $color{#4257b2}left(log 20right)^{2}$ equals $boxed{ 1.69 }$

(f) We would like to evaluate $color{#4257b2}5 log 5$. First, we can use the calculator to determine $color{#4257b2}log 5$ and then multiply by $color{#4257b2}5$ to find the value of $color{#4257b2}5 log 5$.

$$
begin{align*}
5 log 5&=(5)cdot (0.69897)
\ \
&=3.49
end{align*}
$$

So the expression $color{#4257b2}5 log 5$ equals $boxed{ 3.49 }$

Large{$text{$text{color{#c34632}(a) $4.82$ (c) $3.82$ (e) $1.69$
\
\
Large{color{#c34632}(b) $0.8$ (d) $1.35$ (f) $3.49$}$}$