a.)

$$
dfrac{1}{5^2}=dfrac{1}{5cdot 5}=dfrac{1}{25}
$$

Property of exponents:

$a^2 = acdot a$

$$
a^3=acdot acdot a
$$

b.)

$$
11^0=1
$$

For any real number $a$,

$$
a^0 =1
$$

c.)

$$
sqrt{36}=sqrt{6^2}=6
$$

Rule of radicals and exponents:

$sqrt{a^2}=(a^2)^{1/2}=a$

$$
sqrt[n]{a^m}=(a^m)^{1/n}
$$

d.)

$$
sqrt[3]{125}=125^{1/3}=(5^3)^{1/3}=5
$$

e.) $-sqrt{121}=-121^{1/2}=-(11^2)^{1/2}=-11$

f.) $left( sqrt[3]{dfrac{27}{8}}right)^2=left(dfrac{27}{8}right)^{2/3}=left( dfrac{3^3}{2^3}right)^{2/3}=dfrac{3^2}{2^2}$

$$
=dfrac{9}{4}
$$

$$
left(sqrt[n]{dfrac{a}{b}}right)^k=left(dfrac{a}{b}right)^{k/n}=dfrac{a^{k/n}}{b^{k/n}}
$$

a.) $frac{1}{25}$

b.) 1

c.) 6

d.) 5

e.) -11

f.) $frac{9}{4}$

a.) $3^{2+5}=3^7=2187$

Property of exponents:

$a^2 = acdot a$

$$
a^3=acdot acdot a
$$

b.) $(-2)^{12+(-10)}=(-2)^2=4$

c.) $(10)^{9-6}=10^3=1000$

d.) $7^{6+(-3)-(-1)}=7^{6-3+1}=7^4=2401$

Be careful when subtracting integers.

$$
a-(-b)=a+b
$$

e.) $8^{2cdot (1/3)}=8^{frac{2}{3}}=(2^{3})^{2/3}=2^2=4$

$$
(a^b)^{1/c}=a^{b/c}
$$

f.) $4^{left(3/4+1/4-1/2 right)}=4^{3/4+1/4-2/4}$

$$
=4^{1/2}=(2^2)^{1/2}=2
$$

We would like to simplify the following expressions:

(a) $(2m)^{3}$

To simplify this expression we have to use the exponent property which state that:

$$
color{#4257b2}boxed{ (ab)^{c}=a^{c} cdot b^{c} }
$$

Now we can simplify this expression as follows:

$$
color{#4257b2}(2m)^{3}= 2^{3} cdot m^{3}= 8m^{3}
$$

(b) $left(a^{4} b^{5}right)^{-2}$

To simplify this expression we have to use the exponent properties which state that:

$$
color{#4257b2}boxed{ (ab)^{c}=a^{c} cdot b^{c} text{and} a^{-b}=dfrac{1}{a^{b}} }
$$

Now we can simplify this expression as follows:

$$
color{#4257b2} left(a^{4} b^{5}right)^{-2} = dfrac{1}{left(a^{4} b^{5}right)^{2}}= dfrac{1}{left(a^{4}right)^{2} left(b^{5}right)^{2}}= dfrac{1}{a^{8} b^{10}}
$$

(c) $left(16 x^{6}right)^{tfrac{1}{2}}$

To simplify this expression we have to use the exponent property which state that:

$$
color{#4257b2}boxed{ left(a^{b}right)^{c}=(a)^{bc} }
$$

Now we can simplify this expression as follows:

$$
color{#4257b2} left(16 x^{6}right)^{tfrac{1}{2}}= left(4^{2} x^{3 cdot 2}right)^{tfrac{1}{2}} = left(4 x^{3}right)^{2 cdot tfrac{1}{2}} = 4x^{3}
$$

(d) $dfrac{x^{5} y^{2}}{x^{2} y}$

To simplify this expression we have to use the exponent properties which state that:

$$
color{#4257b2}boxed{ dfrac{a^{b}}{a^{c}}=a^{b-c} }
$$

Now we can simplify this expression as follows:

$$
color{#4257b2} dfrac{x^{5} y^{2}}{x^{2} y} = left(x^{5-2}right) left(y^{2-1}right)= x^{3} y
$$

(e) $left(-d^{4}right) left(dfrac{c}{d}right)^{2}$

To simplify this expression we have to use the exponent property which state that:

$$
color{#4257b2}boxed{ left(dfrac{a}{b}right)^{c}=dfrac{a^{c}}{b^{c}} }
$$

Now we can simplify this expression as follows:

$$
color{#4257b2} left(-d^{4}right) left(dfrac{c}{d}right)^{2} = -d^{4} cdot dfrac{c^{2}}{d^{2}} = -dfrac{d^{4} cdot c^{2}}{d^{2}}= -dfrac{cancel{d^{2}} cdot d^{2} cdot c^{2}}{cancel{d^{2}}}=-d^{2} c^{2}
$$

(f) $left(left(x^{3}right)^{-tfrac{1}{3}}right)^{-1}$

To simplify this expression we have to use the exponent properties which state that:

$$
color{#4257b2}boxed{ left(a^{b}right)^{c}=a^{bc} text{and} a^{-1}=dfrac{1}{a} }
$$

Now we can simplify this expression as follows:

$$
color{#4257b2} left(left(x^{3}right)^{-tfrac{1}{3}}right)^{-1} = left(left(xright)^{3 cdot -tfrac{1}{3}}right)^{-1}=left(left(xright)^{ -1}right)^{-1}= left(xright)^{ -1 cdot -1} = x
$$

$$
text{color{#c34632} a) $ 8m^{3}$ b) $ dfrac{1}{a^{8} b^{10}}$ c) $4x^{3}$ \ \

d) $x^{3} y$ e) $-d^{2} c^{2}$ f) $x$}
$$

State the graph for the following expression, then state the domain, range, $y$ intercept and equation of horizontal asymptote.

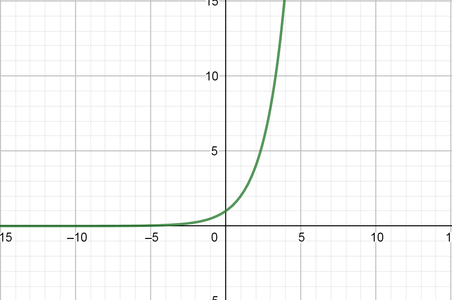
$$
color{#4257b2}text{(a)} y=2^x
$$

From the graph we can state that:

Domain $=(-infty, infty)$ Range$=(0, infty)$

$y$ intercept $y=1$

Equation of the horizontal asymptote is $x$ axis $y=0$

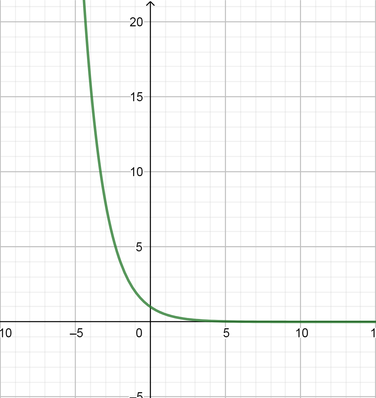
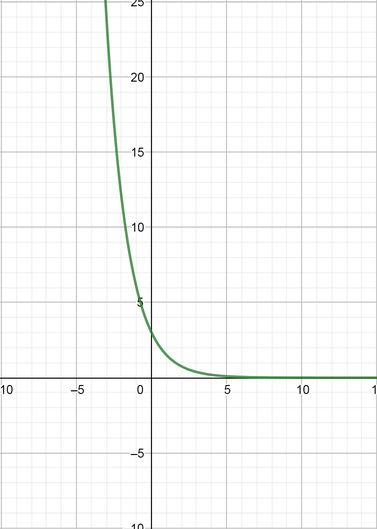
$$
color{#4257b2}text{(b)} y=left(dfrac{1}{2}right)^x
$$

From the graph we can state that:

Domain $=(-infty, infty)$ Range$=(0, infty)$

$y$ intercept $y=1$

Equation of the horizontal asymptote is $x$ axis $y=0$

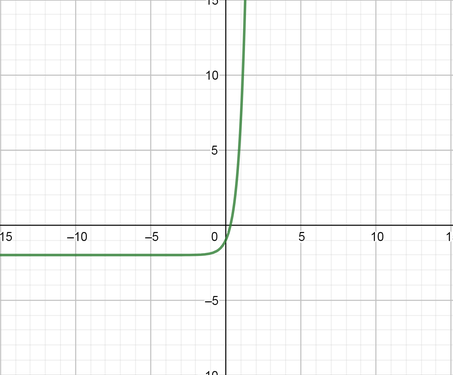
$$
color{#4257b2}text{(c)} y=3^2x-2
$$

From the graph we can state that:

Domain $=(-infty, infty)$ Range$=(-2, infty)$

$y$ intercept $y=-2$

Equation of the horizontal asymptote is $y=-2$

$text{$text{color{#c34632}(a) Domain $=(-infty, infty)$ Range$=(0, infty)$
\ \
$y$ intercept $y=1$ Asymptote equation is $x$ axis $y=0$
\ \
(b) Domain $=(-infty, infty)$ Range$=(0, infty)$
\ \
$y$ intercept $y=1$ Asymptote equation is $x$ axis $y=0$
\ \
(c) Domain $=(-infty, infty)$ Range$=(-2, infty)$
\ \
$y$ intercept $y=-2$ Asymptote equation is $y=-2$
\ \}$}$

Determine the inverse equation for the following expressions.

$$
color{#4257b2}text{(a)} f(x)=3x-6
$$

Substitute the value of $x=y$ as follows:

$$
y=3x-6 x=3y-6
$$

Isolate the $y$ variable on the keft side as follows:

$$
3y=x+6 y=dfrac{x+6}{3}
$$

Substitute the value of $x=y$ as follows:

$$
x=dfrac{y+6}{3} f^{-1}(x)=dfrac{x+6}{3}
$$

$$
color{#4257b2}text{(b)} f(x)=x^2-5
$$

Substitute the value of $x=y$ as follows:

$$
y=x^2-5 x=y^2-5
$$

Isolate the $y$ variable on the keft side as follows:

$$
y^2=x+5
$$

Use square root property as follows:

$$
sqrt{y^2}=sqrt{x+5} y=sqrt{x+5}
$$

Substitute the value of $x=y$ as follows:

$$
x=sqrt{y+5} f^{-1}(x)=sqrt{x+5}
$$

$$
color{#4257b2}text{(c)} f(x)=6x^3
$$

Substitute the value of $x=y$ as follows:

$$
y=6x^3 x=6y^3
$$

Isolate the $y$ variable on the keft side as follows:

$$
y^3=dfrac{x}{6}
$$

Use cubic root property as follows:

$$
sqrt[3]{y^3}=sqrt[3]{dfrac{x}{6}} y=sqrt[3]{dfrac{x}{6}}
$$

Substitute the value of $x=y$ as follows:

$$
x=sqrt[3]{dfrac{y}{6}} f^{-1}(x)=sqrt[3]{dfrac{x}{6}}
$$

$$
color{#4257b2}text{(d)} f(x)=(x-4)^2+3
$$

Substitute the value of $x=y$ as follows:

$$
y=(x-4)^2+3 x=(y-4)^2+3
$$

Isolate the $y$ variable on the left side as follows:

$$
(y-4)^2=x+3
$$

Use square root property as follows:

$$
sqrt{(y-4)^2}=sqrt{x+3} y-4=sqrt{x+3}
$$

$$
y=sqrt{x+3}+4
$$

Substitute the value of $x=y$ as follows:

$$
x=sqrt{y+3}+4 f^{-1}(x)=sqrt{x+3}+4
$$

$$
text{color{#c34632}(a) $f^{-1}(x)=dfrac{x+6}{3}$ (b) $f^{-1}(x)=sqrt{x+5}$
\ \
(c) $f^{-1}(x)=sqrt[3]{dfrac{x}{6}}$ (d) $f^{-1}(x)=y=sqrt{x+3}+4$}
$$

A bacteria culture doubles every $4$ hours. If the rate $100$ in the culture initially. How many bacterial after the following time.

$$
color{#4257b2}text{(a)} 12 text{hours}
$$

We make a general expression represent the bacterial where any time as follows.

$$
a_{4n}=100 (2)^n text{Where:}
$$

$4n=$ total time needed $n=$ number divided by $4$

For $text{color{#4257b2} $12$ hours}$

$$
4n=12 n=dfrac{12}{4} n=3
$$

$$
a_{12}=100(2)^3 a_{12}=100cdot8
$$

$$
a_{12}=800 text{Bacterial}
$$

$$
color{#4257b2}text{(b)} 1 text{day}
$$

$$
a_{4n}=100 (2)^n text{Where:}
$$

$4n=$ total time needed $n=$ number divided by $4$

$$
1text{ day}=24 text{hours}
$$

$$
4n=24 n=dfrac{24}{4} n=6
$$

$$
a_{24}=100(2)^6 a_{12}=100cdot64
$$

$$
a_{24}=6400 text{Bacterial}
$$

$$
color{#4257b2}text{(c)} 3.5 text{days}
$$

$$
a_{4n}=100 (2)^n text{Where:}
$$

$4n=$ total time needed $n=$ number divided by $4$

$$
3.5cdot24=84text{ hours}
$$

$$
4n=84 n=dfrac{84}{4} n=21
$$

$$
a_{84}=100(2)^{21} a_{12}=100cdot2097152
$$

$$
a_{84}=209715200 text{Bacterial}
$$

$$
color{#4257b2}text{(d)} 1 text{week}
$$

$$
a_{4n}=100 (2)^n text{Where:}
$$

$4n=$ total time needed $n=$ number divided by $4$

$$
1text{ week}=7cdot24=168 text{hours}
$$

$$
4n=168 n=dfrac{168}{4} n=42
$$

$$
a_{168}=100(2)^{42} a_{12}=100cdot4398046511104
$$

$$
a_{168}=439804651110400 text{Bacterial}
$$

$color{#c34632}(a) a_{12}=800 text{Bacterial}$ $color{#c34632}(b) a_{24}=6400 text{Bacterial}$

$color{#c34632}(c) a_{84}=209715200 text{Bacterial}$ $color{#c34632}(d) a_{168}=439804651110400 text{Bacterial}$

What will the population be in $2020$. If the population in $2005$ was $15000$ with decline rate of $1.2$ per year.

We make a general expression represent the decline rate after years as follows:

$$
a_n=dfrac{15000}{1.2^n} text{Where} n=text{number of year}
$$

The number of years from $2005$ to $2020$ is $15$ years.

$$
a_{15}=dfrac{15000}{1.2^{15}} a_{15}=dfrac{15000}{15.4070215}
$$

$$
a_{15}=973.582
$$

The population in $2020$ will be $973.582$

$$
text{color{#c34632}The population in $2020$ will be $973.582$}
$$

Compare the graphs of the following expression.

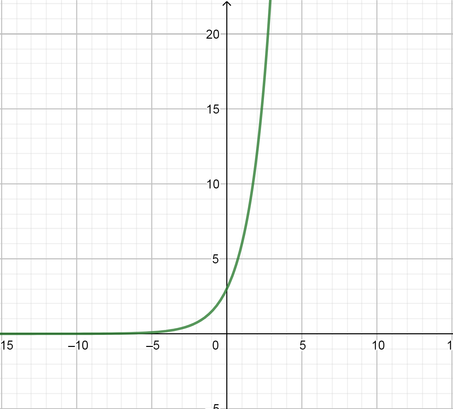
$$
y=3(2^x) y=3left(dfrac{1}{2}right)^x
$$

Fore the first equation:

Domain $=(-infty, infty)$ Range$=(0, infty)$

Equation horizontal asymptote is $x$ axis $y=0$

Fore the second equation:

Domain $=(-infty, infty)$ Range$=(0, infty)$

Equation horizontal asymptote is $x$ axis $y=0$

$$
text{color{#c34632}Domain $=(-infty, infty)$ Range$=(0, infty)$
\ \
Equation horizontal asymptote is $x$ axis $y=0$}
$$