(a) We would like to express the expression $color{#4257b2}2sin 5xcos 5x$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$ where $color{#4257b2}theta$ is considered to be $color{#4257b2}5x$ in our expression, so we can use the double angle formula for the sine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
2sin 5xcos 5x&=sin (2cdot 5x)
\ \
&=boxed{ sin 10x }
end{align*}
$$

(b) We would like to express the expression $color{#4257b2}cos^{2}theta-sin^{2}theta$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the cosine function $color{#4257b2}cos 2theta=cos^{2}theta-sin^{2}theta$, so we can use the double angle formula for the cosine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
cos^{2}theta-sin^{2}theta&=cos (2cdot theta)
\ \
&=boxed{ cos 2theta }
end{align*}
$$

(c) We would like to express the expression $color{#4257b2}1-2sin^{2}3x$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the cosine function $color{#4257b2}cos 2theta=1-2sin^{2}theta$ where $color{#4257b2}theta$ is considered to be $color{#4257b2}3x$ in our expression, so we can use the double angle formula for the cosine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
1-2sin^{2}3x&=cos (2cdot 3x)
\ \
&=boxed{ cos 6x }
end{align*}
$$

(d) We would like to express the expression $color{#4257b2}dfrac{2tan 4x}{1-tan^{2}4x}$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the tangent function $color{#4257b2}tan 2theta=dfrac{2tan theta}{1-tan^{2}theta}$ where $color{#4257b2}theta$ is considered to be $color{#4257b2}4x$ in our expression, so we can use the double angle formula for the tangent function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
dfrac{2tan 4x}{1-tan^{2}4x}&=tan (2cdot 4x)
\ \
&=boxed{ tan 8x }
end{align*}
$$

(e) We would like to express the expression $color{#4257b2}4sin thetacos theta$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$, so we can use the double angle formula for the sine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
4sin thetacos theta&=2cdot 2sin thetacos theta
\ \
&=2sin (2cdot theta)
\ \
&=boxed{ 2sin 2theta }
end{align*}
$$

(f) We would like to express the expression $color{#4257b2}2cos^{2}dfrac{theta}{2}-1$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the cosine function $color{#4257b2}cos 2theta=2cos^{2}theta-1$ where $color{#4257b2}theta$ is considered to be $color{#4257b2}dfrac{theta}{2}$ in our expression, so we can use the double angle formula for the cosine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
2cos^{2}dfrac{theta}{2}-1&=cos left(2cdot dfrac{theta}{2}right)
\ \
&=boxed{ cos theta }
end{align*}
$$

$$
text{color{#c34632}$(a) sin 10x$ $(b) cos 2theta$ $(c) cos 6x$ $(d) tan 8x$ $(e) 2sin 2theta$ $(f) cos theta$}
$$

(a) We would like to express the expression $color{#4257b2}2sin 45text{textdegree}cos 45text{textdegree}$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$ where $color{#4257b2}theta$ is considered to be $color{#4257b2}45text{textdegree}$ in our expression, so we can use the double angle formula for the sine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
2sin 45text{textdegree}cos 45text{textdegree}&=sin (2cdot 45text{textdegree})
\ \
&=sin 90text{textdegree}
\ \
&=boxed{ 1 }
end{align*}
$$

Note that $color{#4257b2}90text{textdegree}$ is a special angle which we know the value of the sine function of it $color{#4257b2}sin 90text{textdegree}=1$

(b) We would like to express the expression $color{#4257b2}cos^{2}30text{textdegree}-sin^{2}30text{textdegree}$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the cosine function $color{#4257b2}cos 2theta=cos^{2}theta-sin^{2}theta$ where $color{#4257b2}theta$ is considered to be $color{#4257b2}30text{textdegree}$ in our expression, so we can use the double angle formula for the cosine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
cos^{2}30text{textdegree}-sin^{2}30text{textdegree}&=cos (2cdot 30text{textdegree})
\ \
&=cos 60text{textdegree}
\ \
&=boxed{ dfrac{1}{2} }
end{align*}
$$

Note that $color{#4257b2}60text{textdegree}$ is a special angle which we know the value of the cosine function of it $color{#4257b2}cos 60text{textdegree}=dfrac{1}{2}$

(c) We would like to express the expression $color{#4257b2}2sin dfrac{pi}{12}cos dfrac{pi}{12}$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$ where $color{#4257b2}theta$ is considered to be $color{#4257b2}dfrac{pi}{12}$ in our expression, so we can use the double angle formula for the sine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
2sin dfrac{pi}{12}cos dfrac{pi}{12}&=sin left(2cdot dfrac{pi}{12}right)
\ \
&=sin dfrac{pi}{6}=boxed{ dfrac{1}{2} }
end{align*}
$$

Note that $color{#4257b2}dfrac{pi}{6}$ is a special angle which we know the value of the sine function of it $color{#4257b2}sin dfrac{pi}{6}=dfrac{1}{2}$

(d) We would like to express the expression $color{#4257b2}cos^{2}dfrac{pi}{12}-sin^{2}dfrac{pi}{12}$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the cosine function $color{#4257b2}cos 2theta=cos^{2}theta-sin^{2}theta$ where $color{#4257b2}theta$ is considered to be $color{#4257b2}dfrac{pi}{12}$ in our expression, so we can use the double angle formula for the cosine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
cos^{2}dfrac{pi}{12}-sin^{2}dfrac{pi}{12}&=cos left(2cdot dfrac{pi}{12}right)
\ \
&=cos dfrac{pi}{6}=boxed{ dfrac{sqrt{3}}{2} }
end{align*}
$$

Note that $color{#4257b2}dfrac{pi}{6}$ is a special angle which we know the value of the cosine function of it $color{#4257b2}cos dfrac{pi}{6}=dfrac{sqrt{3}}{2}$

(e) We would like to express the expression $color{#4257b2}1-2sin^{2}dfrac{3pi}{8}$ as a single trigonometric ratio.

First, we note that our expression is on the form of the double angle formula of the cosine function $color{#4257b2}cos 2theta=1-2sin^{2}theta$ where $color{#4257b2}theta$ is considered to be $color{#4257b2}dfrac{3pi}{8}$ in our expression, so we can use the double angle formula for the cosine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
1-2sin^{2}dfrac{3pi}{8}&=cos left(2cdot dfrac{3pi}{8}right)
\ \
&=cos dfrac{3pi}{4}
\ \
&=boxed{ -dfrac{sqrt{2}}{2} }
end{align*}
$$

Note that $color{#4257b2}dfrac{3pi}{4}$ is a special angle which we know the value of the cosine function of it $color{#4257b2}cos dfrac{3pi}{4}=-dfrac{sqrt{2}}{2}$

(f) We would like to express the expression $color{#4257b2}2tan 60text{textdegree}cos^{2}60text{textdegree}$ as a single trigonometric ratio.

First, we know that $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$, so we can replace $color{#4257b2}tan 60text{textdegree}$ in our expression by $color{#4257b2}dfrac{sin 60text{textdegree}}{cos 60text{textdegree}}$.

$$
2tan 60text{textdegree}cos^{2}60text{textdegree}=2cdot dfrac{sin 60text{textdegree}}{cos 60text{textdegree}}cdot cos^{2}60text{textdegree}=2sin 60text{textdegree}cos 60text{textdegree}
$$

Now we note that our expression is on the form of the double angle formula of the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$ where $color{#4257b2}theta$ is considered to be $color{#4257b2}60text{textdegree}$ in our expression, so we can use the double angle formula for the sine function to rewrite our expression as a single trigonometric ratio.

$$
begin{align*}
2sin 60text{textdegree}cos 60text{textdegree}&=sin (2cdot 60text{textdegree})
\ \
&=sin 120text{textdegree}
\ \
&=boxed{ dfrac{sqrt{3}}{2} }
end{align*}
$$

Note that $color{#4257b2}120text{textdegree}$ is a special angle which we know the value of the sine function of it $color{#4257b2}sin 120text{textdegree}=dfrac{sqrt{3}}{2}$.

$$
text{color{#c34632}$(a) 1$ $(b) dfrac{1}{2}$ $(c) dfrac{1}{2}$ $(d) dfrac{sqrt{3}}{2}$ $(e) -dfrac{sqrt{2}}{2}$ $(f) dfrac{sqrt{3}}{2}$}
$$

(a) We would like to use a double angle formula to rewrite the trigonometric ratio $color{#4257b2}sin 4theta$.

First, we note that our expression is a sine function with angle $color{#4257b2}4 theta$, so we can use the double angle formula for the sine function $color{#4257b2}sin 2x=2sin xcos x$ to rewrite our trigonometric ratio where $color{#4257b2}2x$ is considered to be $color{#4257b2}4theta$ in our trigonometric ratio.

$$
boxed{ sin 4theta=2sin 2thetacos 2theta }
$$

(b) We would like to use a double angle formula to rewrite the trigonometric ratio $color{#4257b2}cos 3x$.

First, we note that our expression is a cosine function with angle $color{#4257b2}3x$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2theta=2cos^{2}theta-1$ to rewrite our trigonometric ratio where $color{#4257b2}2theta$ is considered to be $color{#4257b2}3x$ in our trigonometric ratio.

$$
boxed{ cos 3x=2cos^{2}dfrac{3x}{2}-1 }
$$

(c) We would like to use a double angle formula to rewrite the trigonometric ratio $color{#4257b2}tan x$.

First, we note that our expression is a tangent function with angle $color{#4257b2}x$, so we can use the double angle formula for the tangent function
$color{#4257b2}tan 2theta=dfrac{2tan theta}{1-tan^{2}theta}$ to rewrite our trigonometric ratio where $color{#4257b2}2theta$ is considered to be $color{#4257b2}x$ in our trigonometric ratio.

$$
boxed{ tan x=dfrac{2tan dfrac{x}{2}}{1-tan^{2}dfrac{x}{2}} }
$$

(d) We would like to use a double angle formula to rewrite the trigonometric ratio $color{#4257b2}cos 6theta$.

First, we note that our expression is a cosine function with angle $color{#4257b2}6theta$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2x=2cos^{2}x-1$ to rewrite our trigonometric ratio where $color{#4257b2}2x$ is considered to be $color{#4257b2}6theta$ in our trigonometric ratio.

$$
boxed{ cos 6theta=2cos^{2}3theta-1 }
$$

(e) We would like to use a double angle formula to rewrite the trigonometric ratio $color{#4257b2}sin x$.

First, we note that our expression is a sine function with angle $color{#4257b2}x$, so we can use the double angle formula for the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$ to rewrite our trigonometric ratio where $color{#4257b2}2theta$ is considered to be $color{#4257b2}x$ in our trigonometric ratio.

$$
boxed{ sin x=2sin dfrac{x}{2}cos dfrac{x}{2} }
$$

(f) We would like to use a double angle formula to rewrite the trigonometric ratio $color{#4257b2}tan 5theta$.

First, we note that our expression is a tangent function with angle $color{#4257b2}5theta$, so we can use the double angle formula for the tangent function
$color{#4257b2}tan 2x=dfrac{2tan x}{1-tan^{2}x}$ to rewrite our trigonometric ratio where $color{#4257b2}2x$ is considered to be $color{#4257b2}5theta$ in our trigonometric ratio.

$$
boxed{ tan 5theta=dfrac{2tan dfrac{5theta}{2}}{1-tan^{2}dfrac{5theta}{2}} }
$$

$$
text{color{#c34632}$(a) 2sin 2thetacos 2theta$ $(b) 2cos^{2}dfrac{3x}{2}-1$ $(c) dfrac{2tan dfrac{x}{2}}{1-tan^{2}dfrac{x}{2}}$
\
\
\
Large{color{#c34632}$(d) 2cos^{2}3theta-1$ $(e) 2sin dfrac{x}{2}cos dfrac{x}{2}$ $(f) dfrac{2tan dfrac{5theta}{2}}{1-tan^{2}dfrac{5theta}{2}}$}}
$$

In this problem we would like to evaluate the values of some trigonometric functions $color{#4257b2}sin 2theta, cos 2theta$ and $color{#4257b2}tan 2theta$, so the first step is to find all trigonometric function for the angle $color{#4257b2}theta$ and then substitute in the double angle formulas for these functions.

First, we note that $color{#4257b2}cos theta=dfrac{3}{5}$ where $color{#4257b2}0 < theta < dfrac{pi}{2}$, so we can use the Pythagorean identity $color{#4257b2}sin^{2}theta+cos^{2}theta=1$ to find the value of $color{#4257b2}sin theta$.

$$
sin^{2}theta+cos^{2}theta=1
$$

$$
sin^{2}theta+left(dfrac{3}{5}right)^{2}=1
$$

$$
sin^{2}theta+dfrac{9}{25}=1
$$

$$
sin^{2}theta=1-dfrac{9}{25}=dfrac{16}{25}
$$

Now we can take the square root for each side to find the value of $color{#4257b2}sin theta$

$$
sin theta=pm sqrt{dfrac{16}{25}}=pm dfrac{4}{5}
$$

But we know that $color{#4257b2}0 < theta < dfrac{pi}{2}$ which means that $color{#4257b2}theta$ is in quadrant $1$, so the value of $color{#4257b2}sin theta$ is positive and the negative solution is refused.

$$
boxed{ sin theta=dfrac{4}{5} }
$$

Now we have the values of $color{#4257b2}sin theta$ and $color{#4257b2}cos theta$, so we can use the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$ to find $color{#4257b2}tan theta$

$$
tan theta=dfrac{sin theta}{cos theta}
$$

$$
tan theta=dfrac{dfrac{4}{cancel{5}}}{dfrac{3}{cancel{5}}}
$$

$$
boxed{ tan theta=dfrac{4}{3} }
$$

Now we have the values of all trigonometric functions of the angle $color{#4257b2}theta$, so we can evaluate each requirement as follows:

(a) We would like to evaluate the value of $color{#4257b2}sin 2theta$, so we can use the double angle formula for the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$.

$$
begin{align*}
sin 2theta&=2sin thetacos theta
\ \
&=2cdot dfrac{4}{5}cdot dfrac{3}{5}
\ \
&=boxed{ dfrac{24}{25} }
end{align*}
$$

(b) We would like to evaluate the value of $color{#4257b2}cos 2theta$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2theta=cos^{2}theta-sin^{2}theta$.

$$
begin{align*}
cos 2theta&=cos^{2}theta-sin^{2}theta
\ \
&=left(dfrac{3}{5}right)^{2}-left(dfrac{4}{5}right)^{2}
\ \
&=dfrac{9}{25}-dfrac{16}{25}=boxed{ -dfrac{7}{25} }
end{align*}
$$

(c) We would like to evaluate the value of $color{#4257b2}tan 2theta$, so we can use the double angle formula for the tangent function $color{#4257b2}tan 2theta=dfrac{2tan theta}{1-tan^{2}theta}$.

$$
begin{align*}
tan 2theta&=dfrac{2tan theta}{1-tan^{2}theta}
\ \
&=dfrac{2cdot dfrac{4}{3}}{1-left(dfrac{4}{3}right)^{2}}
\ \
&=boxed{ -dfrac{24}{7} }
end{align*}
$$

$$
text{color{#c34632}$(a) sin 2theta=dfrac{24}{25}$ $(b) cos 2theta=-dfrac{7}{25}$ $(c) tan 2theta=-dfrac{24}{7}$}
$$

In this problem we would like to evaluate the values of some trigonometric functions $color{#4257b2}sin 2theta, cos 2theta$ and $color{#4257b2}tan 2theta$, so the first step is to find all trigonometric function for the angle $color{#4257b2}theta$ and then substitute in the double angle formulas for these functions.

First, we note that $color{#4257b2}tan theta=-dfrac{7}{24}$ where $color{#4257b2}dfrac{pi}{2} < theta < pi$, so we can use the Pythagorean identity $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ to find the value of $color{#4257b2}sec theta$ and then find $color{#4257b2}cos theta$.

$$
1+tan^{2}theta=sec^{2}theta
$$

$$
1+left(-dfrac{7}{24}right)^{2}=sec^{2}theta
$$

$$
1+dfrac{49}{576}=sec^{2}theta
$$

$$
sec^{2}theta=1+dfrac{49}{576}=dfrac{625}{576}
$$

Now we can take the square root for each side to find the value of $color{#4257b2}sec theta$

$$
sec theta=pm sqrt{dfrac{625}{576}}=pm dfrac{25}{24}
$$

But we know that $color{#4257b2}dfrac{pi}{2} < theta < pi$ which means that $color{#4257b2}theta$ is in quadrant $2$, so the value of $color{#4257b2}sec theta$ is negative and the positive solution is refused.

$$
sec theta=-dfrac{25}{24}
$$

Now we can use the identity $color{#4257b2}cos theta=dfrac{1}{sec theta}$ to find $color{#4257b2}cos theta$

$$
cos theta=dfrac{1}{sec theta}=dfrac{1}{-dfrac{25}{24}}
$$

$$
boxed{ cos theta=-dfrac{24}{25} }
$$

Now we have the values of $color{#4257b2}cos theta$ and $color{#4257b2}tan theta$, so we can use the identity $color{#4257b2}sin theta=tan thetacos theta$ to find $color{#4257b2}sin theta$

$$
sin theta=tan thetacos theta
$$

$$
sin theta=left(-dfrac{7}{24}right)left(-dfrac{24}{25}right)
$$

$$
boxed{ sin theta=dfrac{7}{25} }
$$

Now we have the values of all trigonometric functions of the angle $color{#4257b2}theta$, so we can evaluate each requirement as follows:

(a) We would like to evaluate the value of $color{#4257b2}sin 2theta$, so we can use the double angle formula for the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$.

$$
begin{align*}
sin 2theta&=2sin thetacos theta
\ \
&=2cdot dfrac{7}{25}cdot dfrac{-24}{25}
\ \
&=boxed{ -dfrac{336}{625} }
end{align*}
$$

(b) We would like to evaluate the value of $color{#4257b2}cos 2theta$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2theta=cos^{2}theta-sin^{2}theta$.

$$
begin{align*}
cos 2theta&=cos^{2}theta-sin^{2}theta
\ \
&=left(-dfrac{24}{25}right)^{2}-left(dfrac{7}{25}right)^{2}
\ \
&=dfrac{576}{625}-dfrac{49}{625}=boxed{ dfrac{527}{625} }
end{align*}
$$

(c) We would like to evaluate the value of $color{#4257b2}tan 2theta$, so we can use the double angle formula for the tangent function $color{#4257b2}tan 2theta=dfrac{2tan theta}{1-tan^{2}theta}$.

$$
begin{align*}
tan 2theta&=dfrac{2tan theta}{1-tan^{2}theta}
\ \
&=dfrac{2cdot dfrac{-7}{24}}{1-left(dfrac{-7}{24}right)^{2}}
\ \
&=boxed{ -dfrac{336}{527} }
end{align*}
$$

$$
text{color{#c34632}$(a) sin 2theta=-dfrac{336}{625}$ $(b) cos 2theta=dfrac{527}{625}$ $(c) tan 2theta=-dfrac{336}{527}$}
$$

In this problem we would like to evaluate the values of some trigonometric functions $color{#4257b2}sin 2theta, cos 2theta$ and $color{#4257b2}tan 2theta$, so the first step is to find all trigonometric function for the angle $color{#4257b2}theta$ and then substitute in the double angle formulas for these functions.

First, we note that $color{#4257b2}sin theta=-dfrac{12}{13}$ where $color{#4257b2}dfrac{3pi}{2} < theta < 2pi$, so we can use the Pythagorean identity $color{#4257b2}sin^{2}theta+cos^{2}theta=1$ to find the value of $color{#4257b2}cos theta$.

$$
sin^{2}theta+cos^{2}theta=1
$$

$$
left(-dfrac{12}{13}right)^{2}+cos^{2}theta=1
$$

$$
dfrac{144}{169}+cos^{2}theta=1
$$

$$
cos^{2}theta=1-dfrac{144}{169}=dfrac{25}{169}
$$

Now we can take the square root for each side to find the value of $color{#4257b2}cos theta$

$$
cos theta=pm sqrt{dfrac{25}{169}}=pm dfrac{5}{13}
$$

But we know that $color{#4257b2}dfrac{3pi}{2} < theta < 2pi$ which means that $color{#4257b2}theta$ is in quadrant $4$, so the value of $color{#4257b2}cos theta$ is positive and the negative solution is refused.

$$
boxed{ cos theta=dfrac{5}{13} }
$$

Now we have the values of $color{#4257b2}sin theta$ and $color{#4257b2}cos theta$, so we can use the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$ to find $color{#4257b2}tan theta$

$$
tan theta=dfrac{sin theta}{cos theta}
$$

$$
tan theta=dfrac{-dfrac{12}{cancel{13}}}{dfrac{5}{cancel{13}}}
$$

$$
boxed{ tan theta=-dfrac{12}{5} }
$$

Now we have the values of all trigonometric functions of the angle $color{#4257b2}theta$, so we can evaluate each requirement as follows:

(a) We would like to evaluate the value of $color{#4257b2}sin 2theta$, so we can use the double angle formula for the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$.

$$
begin{align*}
sin 2theta&=2sin thetacos theta
\ \
&=2cdot dfrac{-12}{13}cdot dfrac{5}{13}
\ \
&=boxed{ -dfrac{120}{169} }
end{align*}
$$

(b) We would like to evaluate the value of $color{#4257b2}cos 2theta$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2theta=cos^{2}theta-sin^{2}theta$.

$$
begin{align*}
cos 2theta&=cos^{2}theta-sin^{2}theta
\ \
&=left(dfrac{5}{13}right)^{2}-left(-dfrac{12}{13}right)^{2}
\ \
&=dfrac{25}{169}-dfrac{144}{169}=boxed{ -dfrac{119}{169} }
end{align*}
$$

(c) We would like to evaluate the value of $color{#4257b2}tan 2theta$, so we can use the double angle formula for the tangent function $color{#4257b2}tan 2theta=dfrac{2tan theta}{1-tan^{2}theta}$.

$$
begin{align*}
tan 2theta&=dfrac{2tan theta}{1-tan^{2}theta}
\ \
&=dfrac{2cdot dfrac{-12}{5}}{1-left(-dfrac{12}{5}right)^{2}}
\ \
&=boxed{ dfrac{120}{119} }
end{align*}
$$

$$
text{color{#c34632}$(a) sin 2theta=-dfrac{120}{169}$ $(b) cos 2theta=-dfrac{119}{169}$ $(c) tan 2theta=dfrac{120}{119}$}
$$

In this problem we would like to evaluate the values of some trigonometric functions $color{#4257b2}sin 2theta, cos 2theta$ and $color{#4257b2}tan 2theta$, so the first step is to find all trigonometric function for the angle $color{#4257b2}theta$ and then substitute in the double angle formulas for these functions.

First, we note that $color{#4257b2}cos theta=-dfrac{4}{5}$ where $color{#4257b2}dfrac{pi}{2} < theta < pi$, so we can use the Pythagorean identity $color{#4257b2}sin^{2}theta+cos^{2}theta=1$ to find the value of $color{#4257b2}sin theta$.

$$
sin^{2}theta+cos^{2}theta=1
$$

$$
sin^{2}theta+left(-dfrac{4}{5}right)^{2}=1
$$

$$
sin^{2}theta+dfrac{16}{25}=1
$$

$$
sin^{2}theta=1-dfrac{16}{25}=dfrac{9}{25}
$$

Now we can take the square root for each side to find the value of $color{#4257b2}sin theta$

$$
sin theta=pm sqrt{dfrac{9}{25}}=pm dfrac{3}{5}
$$

But we know that $color{#4257b2}dfrac{pi}{2} < theta < pi$ which means that $color{#4257b2}theta$ is in quadrant $2$, so the value of $color{#4257b2}sin theta$ is positive and the negative solution is refused.

$$
boxed{ sin theta=dfrac{3}{5} }
$$

Now we have the values of $color{#4257b2}sin theta$ and $color{#4257b2}cos theta$, so we can use the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$ to find $color{#4257b2}tan theta$

$$
tan theta=dfrac{sin theta}{cos theta}
$$

$$
tan theta=dfrac{dfrac{3}{cancel{5}}}{-dfrac{4}{cancel{5}}}
$$

$$
boxed{ tan theta=-dfrac{3}{4} }
$$

Now we have the values of all trigonometric functions of the angle $color{#4257b2}theta$, so we can evaluate each requirement as follows:

(a) We would like to evaluate the value of $color{#4257b2}sin 2theta$, so we can use the double angle formula for the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$.

$$
begin{align*}
sin 2theta&=2sin thetacos theta
\ \
&=2cdot dfrac{3}{5}cdot dfrac{-4}{5}
\ \
&=boxed{ -dfrac{24}{25} }
end{align*}
$$

(b) We would like to evaluate the value of $color{#4257b2}cos 2theta$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2theta=cos^{2}theta-sin^{2}theta$.

$$
begin{align*}
cos 2theta&=cos^{2}theta-sin^{2}theta
\ \
&=left(-dfrac{4}{5}right)^{2}-left(dfrac{3}{5}right)^{2}
\ \
&=dfrac{16}{25}-dfrac{9}{25}=boxed{ dfrac{7}{25} }
end{align*}
$$

(c) We would like to evaluate the value of $color{#4257b2}tan 2theta$, so we can use the double angle formula for the tangent function $color{#4257b2}tan 2theta=dfrac{2tan theta}{1-tan^{2}theta}$.

$$
begin{align*}
tan 2theta&=dfrac{2tan theta}{1-tan^{2}theta}
\ \
&=dfrac{2cdot dfrac{-3}{4}}{1-left(dfrac{-3}{4}right)^{2}}
\ \
&=boxed{ -dfrac{24}{7} }
end{align*}
$$

$$
text{color{#c34632}$(a) sin 2theta=-dfrac{24}{25}$ $(b) cos 2theta=dfrac{7}{25}$ $(c) tan 2theta=-dfrac{24}{7}$}
$$

We would like to determine the value of $color{#4257b2}a$ in the equation
$$
color{#4257b2}2tan x-tan 2x+2a=1-tan 2xtan^{2}x
$$

First, to find the value of $color{#4257b2}a$ we need to make it alone in the left side, so we can add $color{#4257b2}tan 2x-2tan x$ to each side.

$$
2tan x-tan 2x+2a=1-tan 2xtan^{2}x
$$

$$
2tan x-tan 2x+2a+tan 2x-2tan x=1-tan 2xtan^{2}x+tan 2x-2tan x
$$

$$
2a=left(tan 2x-tan 2xtan^{2}xright)+1-2tan x
$$

Now we can take $color{#4257b2}tan 2x$ as a common factor from the first two terms in the right side

$$
2a=tan 2xleft(1-tan^{2}xright)+1-2tan x
$$

Now we can use the double angle formula for the tangent function where $color{#4257b2}tan 2x=dfrac{2tan x}{1-tan^{2}x}$

$$
2a=left(dfrac{2tan x}{1-tan^{2}x}right)left(1-tan^{2}xright)+1-2tan x
$$

Now we can cancel the term $color{#4257b2}1-tan^{2}x$ from the numerator and denominator to simplify

$$
2a=left(dfrac{2tan x}{cancel{1-tan^{2}x}}right)left(cancel{1-tan^{2}x}right)+1-2tan x
$$

$$
2a=2tan x+1-2tan x
$$

$$
2a=cancel{2tan x}+1cancel{-2tan x}
$$

$$
2a=1
$$

Now the final step is to divide the two sides by $2$ to find the value of $color{#4257b2}a$.

$$
boxed{ a=dfrac{1}{2} }
$$

$$
color{#c34632}a=dfrac{1}{2}
$$

We would like to find the sine of $color{#4257b2}dfrac{pi}{8}$ if we know that $color{#4257b2}cos dfrac{pi}{4}=dfrac{1}{sqrt{2}}$. First, we note that the angle $color{#4257b2}dfrac{pi}{4}$ is a double from the angle $color{#4257b2}dfrac{pi}{8}$, so if we supposed that $color{#4257b2}2theta=dfrac{pi}{4}$, then $color{#4257b2}theta=dfrac{pi}{8}$. As a result to find the sine of the angle $color{#4257b2}dfrac{pi}{8}$ which supposed to be $color{#4257b2}theta$ from the fact $color{#4257b2}cos dfrac{pi}{4}=dfrac{1}{sqrt{2}}$ which supposed to be $color{#4257b2}cos 2theta$ we need to know a relation between $color{#4257b2}cos 2theta$ and $color{#4257b2}sin theta$ and this relation is the double angle formula for the cosine function where $color{#4257b2}cos 2theta=1-2sin^{2}theta$.

$$
cos 2theta=1-2sin^{2}theta
$$

$$
cos dfrac{pi}{4}=1-2sin^{2}dfrac{pi}{8}
$$

$$
dfrac{1}{sqrt{2}}=1-2sin^{2}dfrac{pi}{8}
$$

$$
2sin^{2}dfrac{pi}{8}=1-dfrac{1}{sqrt{2}}=dfrac{sqrt{2}-1}{sqrt{2}}
$$

$$
sin^{2}dfrac{pi}{8}=dfrac{sqrt{2}-1}{2sqrt{2}}
$$

Note that we substituted $color{#4257b2}2theta=dfrac{pi}{4}$ and $color{#4257b2}theta=dfrac{pi}{8}$ in the double angle formula.

Now we can take the square root for each side to find $color{#4257b2}sin dfrac{pi}{8}$.

$$
sin dfrac{pi}{8}=pm sqrt{dfrac{sqrt{2}-1}{2sqrt{2}}}
$$

But we know that the angle $color{#4257b2}dfrac{pi}{8}$ is in quadrant $1$, so the value of the sine function for this angle is positive.

$$
boxed{ sin dfrac{pi}{8}=sqrt{dfrac{sqrt{2}-1}{2sqrt{2}}} }
$$

$$
color{#c34632}sin dfrac{pi}{8}=sqrt{dfrac{sqrt{2}-1}{2sqrt{2}}}
$$

We would like to find the cosine of $color{#4257b2}dfrac{pi}{12}$ if we know that $color{#4257b2}cos dfrac{pi}{6}=dfrac{sqrt{3}}{2}$. First, we note that the angle $color{#4257b2}dfrac{pi}{6}$ is a double from the angle $color{#4257b2}dfrac{pi}{12}$, so if we supposed that $color{#4257b2}2theta=dfrac{pi}{6}$, then $color{#4257b2}theta=dfrac{pi}{12}$. As a result to find the cosine of the angle $color{#4257b2}dfrac{pi}{12}$ which supposed to be $color{#4257b2}theta$ from the fact $color{#4257b2}cos dfrac{pi}{6}=dfrac{sqrt{3}}{2}$ which supposed to be $color{#4257b2}cos 2theta$ we need to know a relation between $color{#4257b2}cos 2theta$ and $color{#4257b2}cos theta$ and this relation is the double angle formula for the cosine function where $color{#4257b2}cos 2theta=2cos^{2}theta-1$.

$$
cos 2theta=2cos^{2}theta-1
$$

$$
cos dfrac{pi}{6}=2cos^{2}dfrac{pi}{12}-1
$$

$$
dfrac{sqrt{3}}{2}=2cos^{2}dfrac{pi}{12}-1
$$

$$
2cos^{2}dfrac{pi}{12}=dfrac{sqrt{3}}{2}+1=dfrac{sqrt{3}+2}{2}
$$

$$
cos^{2}dfrac{pi}{12}=dfrac{sqrt{3}+2}{4}
$$

Note that we substituted $color{#4257b2}2theta=dfrac{pi}{6}$ and $color{#4257b2}theta=dfrac{pi}{12}$ in the double angle formula.

Now we can take the square root for each side to find $color{#4257b2}cos dfrac{pi}{12}$.

$$
cos dfrac{pi}{12}=pm sqrt{dfrac{sqrt{3}+2}{4}}=pm dfrac{sqrt{sqrt{3}+2}}{2}
$$

But we know that the angle $color{#4257b2}dfrac{pi}{12}$ is in quadrant $1$, so the value of the cosine function for this angle is positive.

$$
boxed{ cos dfrac{pi}{12}=dfrac{sqrt{sqrt{3}+2}}{2} }
$$

$$
color{#c34632}cos dfrac{pi}{12}=dfrac{sqrt{sqrt{3}+2}}{2}
$$

*(a)* The double angle identity for the sine and cosine function yields
$$
begin{align*}
sin 2x&=2sin xcos x\
cos 2x&=cos^2x-sin^2x=1-2sin^2 x.end{align*}tag{1}$$
Using these identities we can transform and evaluate the sine function of the given angle.

Rewriting $4x=2cdot2x$ we can apply the double angle identity for the sine function of an angle $2x$, and then apply the regular double angle identities to simplify the expression, as follows:
$$
begin{align*}
sin 4x&=sin2(2x)\&=2sin 2xcos 2x\
&=2(2sin xcos x)(1-2sin^2x)\
&=4sin xcos x-8sin^3 xcos x.quadquad (2)end{align*}$$

*(b)* We know that $sin frac{pi}{3}=frac{sqrt{3}}{2}$ and $cos frac{pi}{3}=frac{1}{2}$. Applying the double angle identities we can obtain the values of sine and cosine function of an angle $ frac{2pi}{3}$. Those yields:
$$
begin{align*}
sin 2 dfrac{pi}{3}&=2sin dfrac{pi}{3}cos dfrac{pi}{3}=2cdot dfrac{sqrt{3}}{2}cdot dfrac{1}{2}= dfrac{sqrt{3}}{2}quad(3)\
cos 2 dfrac{pi}{3}&=1-2sin^2 dfrac{pi}{3}=1-2cdotleft( dfrac{sqrt{3}}{2} right)^2=1-2cdot dfrac{3}{4}=- dfrac{1}{2}.end{align*}$$

The angle $frac{8pi}{3}$ we can rewrite as $4cdot frac{2pi}{3}$ and apply the Eq.$(2)$. It yields:
$$
begin{align*}
sin left(4cdot dfrac{2pi}{3}right)&=4sin dfrac{2pi}{3}cos dfrac{2pi}{3}-8sin^3 dfrac{2pi}{3}cos dfrac{2pi}{3}\
&=4cdotdfrac{sqrt{3}}{2}cdot left(-dfrac{1}{2} right)-8cdot left(dfrac{sqrt{3}}{2} right)^3cdot left(-dfrac{1}{2} right)\
&=-sqrt{3}+4cdotdfrac{3sqrt{3}}{8}\
&=-sqrt{3}+dfrac{3sqrt{3}}{2}\
&=-dfrac{2sqrt{3}}{2}+dfrac{3sqrt{3}}{2}\
&=dfrac{sqrt{3}}{2}.
end{align*}$$

Comparing this result to the result we’ve obtained in Eq. $(3)$, we can conclude that
$$
sin dfrac{2pi}{3}=sin dfrac{8pi}{3}.$$

We would like to use the appropriate compound angle formula and double angle formula to develop a formula for $color{#4257b2}sin 3theta$ in terms of $color{#4257b2}cos theta$ and $color{#4257b2}sin theta$.

First, we know that $color{#4257b2}3theta=2theta+theta$, so we can rewrite $color{#4257b2}sin 3theta$ as $color{#4257b2}sin left(2theta+thetaright)$. Now we have a sine function which consists of two sum angles, so we can use the addition formula for the sine function where $color{#4257b2}sin (a+b)=sin acos b+cos asin b$

$$
begin{align*}
sin 3theta&=sin left(2theta+thetaright)
\ \
&=sin 2thetacos theta+cos 2thetasin theta
end{align*}
$$

Now we have two terms each one of them contains a trigonometric function with a double angle, so we can use the double angle formulas for the sine and cosine functions $color{#4257b2}sin 2theta=2sin thetacos theta$ and $color{#4257b2}cos 2theta=cos^{2}theta-sin^{2}theta$ to rewrite our expression in terms of $color{#4257b2}cos theta$ and $color{#4257b2}sin theta$ only.

$$
begin{align*}
sin 2thetacos theta+cos 2thetasin theta&=left(2sin thetacos thetaright)cos theta+left(cos^{2}theta-sin^{2}thetaright)sin theta
\ \
&=2sin thetacos^{2}theta+sin thetacos^{2}theta-sin^{3}theta
\ \
&=3sin thetacos^{2}theta-sin^{3}theta
end{align*}
$$

So the function $color{#4257b2}sin 3theta$ can be written as $boxed{ 3sin thetacos^{2}theta-sin^{3}theta }$

We would like to use the appropriate compound angle formula and double angle formula to develop a formula for $color{#4257b2}cos 3theta$ in terms of $color{#4257b2}cos theta$ and $color{#4257b2}sin theta$.

First, we know that $color{#4257b2}3theta=2theta+theta$, so we can rewrite $color{#4257b2}cos 3theta$ as $color{#4257b2}cos left(2theta+thetaright)$. Now we have a cosine function which consists of two sum angles, so we can use the addition formula for the cosine function where $color{#4257b2}cos (a+b)=cos acos b-sin asin b$

$$
begin{align*}
cos 3theta&=cos left(2theta+thetaright)
\ \
&=cos 2thetacos theta-sin 2thetasin theta
end{align*}
$$

Now we have two terms each one of them contains a trigonometric function with a double angle, so we can use the double angle formulas for the sine and cosine functions $color{#4257b2}sin 2theta=2sin thetacos theta$ and $color{#4257b2}cos 2theta=cos^{2}theta-sin^{2}theta$ to rewrite our expression in terms of $color{#4257b2}cos theta$ and $color{#4257b2}sin theta$ only.

$$
begin{align*}
cos 2thetacos theta-sin 2thetasin theta&=left(cos^{2}theta-sin^{2}thetaright)cos theta-left(2sin thetacos thetaright)sin theta
\ \
&=cos^{3}theta-sin^{2}thetacos theta-2sin^{2}thetacos theta
\ \
&=cos^{3}theta-3sin^{2}thetacos theta
end{align*}
$$

So the function $color{#4257b2}cos 3theta$ can be written as $boxed{ cos^{3}theta-3sin^{2}thetacos theta }$

We would like to use the appropriate compound angle formula and double angle formula to develop a formula for $color{#4257b2}tan 3theta$ in terms of $color{#4257b2}tan theta$.

First, we know that $color{#4257b2}3theta=2theta+theta$, so we can rewrite $color{#4257b2}tan 3theta$ as $color{#4257b2}tan left(2theta+thetaright)$. Now we have a tangent function which consists of two sum angles, so we can use the addition formula for the tangent function where
$color{#4257b2}tan (a+b)=dfrac{tan a+tan b}{1-tan atan b}$

$$
begin{align*}
tan 3theta&=tan left(2theta+thetaright)
\ \
&=dfrac{tan 2theta+tan theta}{1-tan 2thetatan theta}
end{align*}
$$

Now we have fraction the numerator and denominator of it contain a tangent function with a double angle, so we can use the double angle formula for the tangent function $color{#4257b2}tan 2theta=dfrac{2tan theta}{1-tan^{2}theta}$ to rewrite our expression in terms of $color{#4257b2}tan theta$ only.

$$
begin{align*}
dfrac{tan 2theta+tan theta}{1-tan 2thetatan theta}&=dfrac{dfrac{2tan theta}{1-tan^{2}theta}+tan theta}{1-dfrac{2tan theta}{1-tan^{2}theta}cdot tan theta}
\ \
&=dfrac{dfrac{2tan theta+tan thetaleft(1-tan^{2}thetaright)}{1-tan^{2}theta}}{1-dfrac{2tan^{2}theta}{1-tan^{2}theta}}
\ \
&=dfrac{dfrac{2tan theta+tan theta-tan^{3}theta}{1-tan^{2}theta}}{dfrac{1-tan^{2}theta-2tan^{2}theta}{1-tan^{2}theta}}
\ \
&=dfrac{dfrac{3tan theta-tan^{3}theta}{cancel{1-tan^{2}theta}}}{dfrac{1-3tan^{2}theta}{cancel{1-tan^{2}theta}}}
\ \
&=dfrac{3tan theta-tan^{3}theta}{1-3tan^{2}theta}
end{align*}
$$

So the function $color{#4257b2}tan 3theta$ can be written as $boxed{ dfrac{3tan theta-tan^{3}theta}{1-3tan^{2}theta} }$

$$
text{color{#c34632}$(a) 3sin thetacos^{2}theta-3sin^{3}theta$ $(b) cos^{3}theta-3sin^{2}thetacos theta$ $(c) dfrac{3tan theta-tan^{3}theta}{1-3tan^{2}theta}$}
$$

In this problem we would like to determine the values of some trigonometric functions $color{#4257b2}sin 2x, cos 2x, cos dfrac{x}{2}$ and $color{#4257b2}sin 3x$, so the first step is to find the sine and cosine functions for the angle $color{#4257b2}x$ and then substitute in the double angle formulas for these functions.

First, we note that $color{#4257b2}sin^{2}x=dfrac{8}{9}$ where $color{#4257b2}dfrac{pi}{2} < x < pi$, so we can take the square root for each side to find the value of $color{#4257b2}sin x$

$$
sin^{2}x=dfrac{8}{9}
$$

$$
sin x=pm sqrt{dfrac{8}{9}}=pm dfrac{2sqrt{2}}{3}
$$

But we know that $color{#4257b2}dfrac{pi}{2} < x < pi$ which means that $color{#4257b2}x$ is in quadrant $2$, so the value of $color{#4257b2}sin x$ is positive and the negative solution is refused.

$$
boxed{ sin x=dfrac{2sqrt{2}}{3} }
$$

Also since we have the value of $color{#4257b2}sin^{2}x=dfrac{8}{9}$, so we can use the Pythagorean identity $color{#4257b2}sin^{2}theta+cos^{2}theta=1$ to find $color{#4257b2}cos x$.

$$
sin^{2}x+cos^{2}x=1
$$

$$
dfrac{8}{9}+cos^{2}x=1
$$

$$
cos^{2}x=1-dfrac{8}{9}=dfrac{1}{9}
$$

Now we can take the square root for each side to find the value of $color{#4257b2}cos x$

$$
cos x=pm sqrt{dfrac{1}{9}}=pm dfrac{1}{3}
$$

But we know that $color{#4257b2}dfrac{pi}{2} < x < pi$ which means that $color{#4257b2}x$ is in quadrant $2$, so the value of $color{#4257b2}cos x$ is negative and the positive solution is refused.

$$
boxed{ cos x=-dfrac{1}{3} }
$$

Now we have the values of the sine and cosine functions of the angle $color{#4257b2}x$, so we can evaluate each requirement as follows:

(a) We would like to evaluate the value of $color{#4257b2}sin 2x$, so we can use the double angle formula for the sine function $color{#4257b2}sin 2x=2sin xcos x$.

$$
begin{align*}
sin 2x&=2sin xcos x
\ \
&=2cdot dfrac{2sqrt{2}}{3}cdot dfrac{-1}{3}
\ \
&=boxed{ -dfrac{4sqrt{2}}{9} }
end{align*}
$$

(b) We would like to evaluate the value of $color{#4257b2}cos 2x$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2x=cos^{2}x-sin^{2}x$.

$$
begin{align*}
cos 2x&=cos^{2}x-sin^{2}x
\ \
&=left(-dfrac{1}{3}right)^{2}-left(dfrac{2sqrt{2}}{3}right)^{2}
\ \
&=dfrac{1}{9}-dfrac{8}{9}=boxed{ -dfrac{7}{9} }
end{align*}
$$

(c) We would like to evaluate the value of $color{#4257b2}cos dfrac{x}{2}$, so we can develop a formula for it using the double angle formula for the cosine function $color{#4257b2}cos x=2cos^{2}dfrac{x}{2}-1$.

$$
cos x=2cos^{2}dfrac{x}{2}-1
$$

$$
2cos^{2}dfrac{x}{2}=1+cos x
$$

$$
cos^{2}dfrac{x}{2}=dfrac{1+cos x}{2}
$$

Now we can take the square root for each side to find $color{#4257b2}cos dfrac{x}{2}$

$$
cos dfrac{x}{2}=pm sqrt{dfrac{1+cos x}{2}}
$$

Now we we can use this formula to find the value of $color{#4257b2}cos dfrac{x}{2}$ since we know the value of $color{#4257b2}cos x=-dfrac{1}{3}$.

$$
cos dfrac{x}{2}=pm sqrt{dfrac{1+cos x}{2}}
$$

$$
cos dfrac{x}{2}=pm sqrt{dfrac{1-dfrac{1}{3}}{2}}
$$

$$
cos dfrac{x}{2}=pm sqrt{dfrac{dfrac{2}{3}}{2}}
$$

$$
cos dfrac{x}{2}=pm sqrt{dfrac{1}{3}}=pm dfrac{1}{sqrt{3}}
$$

But we know that $color{#4257b2}dfrac{pi}{2} < x < pi$, so to know in which quadrant $color{#4257b2}dfrac{x}{2}$ terminates we can divide each side by $2$

$$
dfrac{pi}{2} < x < pi
$$

$$
dfrac{pi}{4} < dfrac{x}{2} < dfrac{pi}{2}
$$

So the angle $color{#4257b2}dfrac{x}{2}$ is in quadrant $1$ where the cosine function is positive in that quadrant.

$$
boxed{ cos dfrac{x}{2}=dfrac{1}{sqrt{3}} }
$$

(d) We would like to evaluate the value of $color{#4257b2}sin 3x$. First, we know that $color{#4257b2}3x=2x+x$, so we can rewrite $color{#4257b2}sin 3x$ as $color{#4257b2}sin left(2x+xright)$. Now we can use the adiition formula for the sine function $color{#4257b2}sin (a+b)=sin acos b+cos asin b$.

$$
begin{align*}
sin 3x&=sin left(2x+xright)
\ \
&=sin 2xcos x+cos 2xsin x
\ \
&=dfrac{-4sqrt{2}}{9}cdot dfrac{-1}{3}+dfrac{-7}{9}cdot dfrac{2sqrt{2}}{3}
\
&=dfrac{4sqrt{2}}{27}-dfrac{14sqrt{2}}{27}
\
&=boxed{ -dfrac{10sqrt{2}}{27} }
end{align*}
$$

Note that we substituted the values of $color{#4257b2}sin 2x$ and $color{#4257b2}cos 2x$ from the first two requirements (a) and (b).

$$
text{color{#c34632}$(a) sin 2x=-dfrac{4sqrt{2}}{9}$ $(b) cos 2x=-dfrac{7}{9}$
\
\
$(c) cos dfrac{x}{2}=dfrac{1}{sqrt{3}}$ $(d) sin 3x=-dfrac{10sqrt{2}}{27}$}
$$

(a) We would like to sketch the function $color{#4257b2}f(x)=sin xcos x$ using the double angle formulas. First, we note that the function is on the form of the double angle formula for the sine function $color{#4257b2}sin 2x=2sin xcos x$ but the difference is that our function is not multiplied by $2$, so we can multiply and divide our function by $2$.

$$
f(x)=sin xcos x
$$

$$
f(x)=dfrac{1}{2}left(2sin xcos xright)
$$

Now our function became on the form of the double angle formula of the sine function, so we can simplify it as follows:

$$
f(x)=dfrac{1}{2}left(2sin xcos xright)
$$

$$
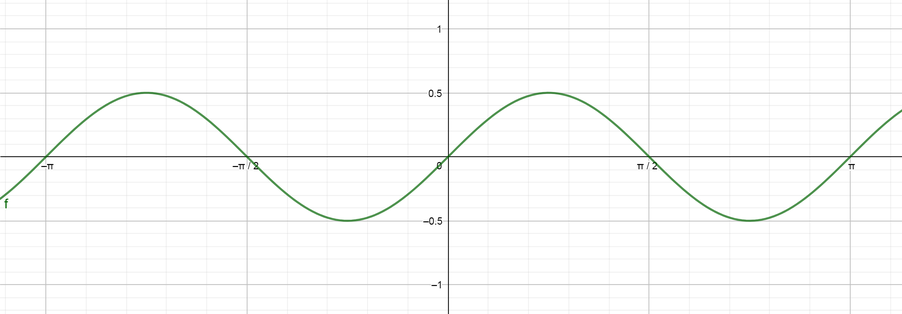
f(x)=dfrac{1}{2} sin 2x
$$

Now our function is a sine function multiplied by $dfrac{1}{2}$ and the period of it is $color{#4257b2}dfrac{2pi}{2}=pi$, so we can graph it using these information.

(b) We would like to sketch the function $color{#4257b2}f(x)=2cos^{2} x$ using the double angle formulas. First, we note that the function is on the form of the double angle formula for the cosine function $color{#4257b2}cos 2x=2cos^{2}x-1$ but the difference is that our function doesn’t include $-1$, so we can add and subtract $1$ from our function.

$$
f(x)=2cos^{2}x
$$

$$
f(x)=2cos^{2}x+1-1
$$

$$
f(x)=left(2cos^{2}x-1right)+1
$$

Now our function became on the form of the double angle formula of the cosine function, so we can simplify it as follows:

$$
f(x)=left(2cos^{2}x-1right)+1
$$

$$
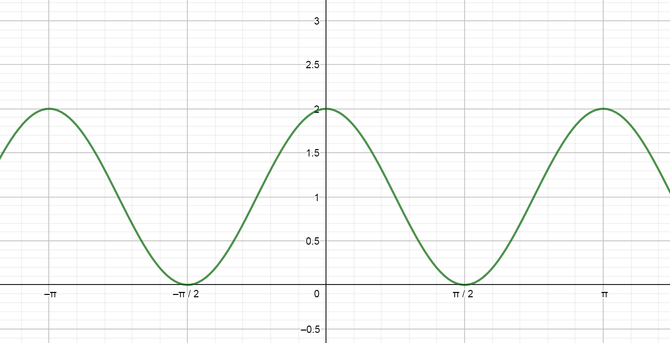
f(x)=cos 2x+1
$$

Now our function is a cosine function shifted by $1$ and the period of it is $color{#4257b2}dfrac{2pi}{2}=pi$, so we can graph it using these information.

(a) We would like to sketch the function $color{#4257b2}f(x)=dfrac{tan x}{1-tan^{2}x}$ using the double angle formulas. First, we note that the function is on the form of the double angle formula for the tangent function $color{#4257b2}tan 2x=dfrac{2tan x}{1-tan^{2}x}$ but the difference is that our function is not multiplied by $2$, so we can multiply and divide our function by $2$.

$$
f(x)=dfrac{tan x}{1-tan^{2}x}
$$

$$
f(x)=dfrac{1}{2}left(dfrac{2tan x}{1-tan^{2}x}right)
$$

Now our function became on the form of the double angle formula of the tangent function, so we can simplify it as follows:

$$
f(x)=dfrac{1}{2}left(dfrac{2tan x}{1-tan^{2}x}right)
$$

$$
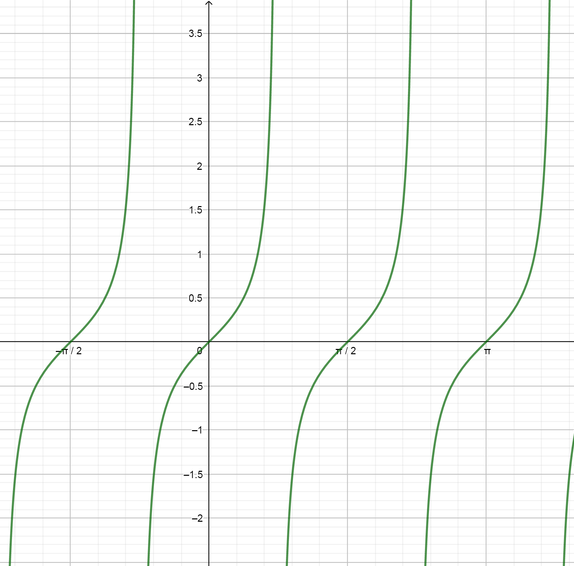
f(x)=dfrac{1}{2} tan 2x
$$

Now our function is a tangent function multiplied by $dfrac{1}{2}$ and the period of it is $color{#4257b2}dfrac{2pi}{4}=dfrac{pi}{2}$, so we can graph it using these information.

$$
text{color{#c34632}$(a) dfrac{1}{2} sin 2x$ $(b) cos 2x+1$ $(c) dfrac{1}{2} tan 2x$}
$$

(a) We would like to eliminate $A$ from each pair of equations
$color{#4257b2}x=tan 2A, y=tan A$ to find an equation that relates $x$ to $y$. First, we note that $color{#4257b2}x=tan 2A$, so we can use the double angle formula for the tangent function $color{#4257b2}tan 2A=dfrac{2tan A}{1-tan^{2}A}$.

$$
x=tan 2A
$$

$$
x=dfrac{2tan A}{1-tan^{2}A} (1)
$$

Now we note that $color{#4257b2}x$ is a function of $color{#4257b2}tan A$ and we know that $color{#4257b2}y=tan A$, so we can replace each $color{#4257b2}tan A$ from equation $(1)$ by $color{#4257b2}y$.

$$
x=dfrac{2tan A}{1-tan^{2}A}
$$

$$
x=dfrac{2y}{1-y^{2}}
$$

So the relation between $color{#4257b2}x$ and $color{#4257b2}y$ is $boxed{ x=dfrac{2y}{1-y^{2}} }$

(b) We would like to eliminate $A$ from each pair of equations
$color{#4257b2}x=cos 2A, y=cos A$ to find an equation that relates $x$ to $y$. First, we note that $color{#4257b2}x=cos 2A$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2A=2cos^{2}A-1$.

$$
x=cos 2A
$$

$$
x=2cos^{2}A-1 (2)
$$

Now we note that $color{#4257b2}x$ is a function of $color{#4257b2}cos A$ and we know that $color{#4257b2}y=cos A$, so we can replace each $color{#4257b2}cos A$ from equation $(2)$ by $color{#4257b2}y$.

$$
x=2cos^{2}A-1
$$

$$
x=2y^{2}-1
$$

So the relation between $color{#4257b2}x$ and $color{#4257b2}y$ is $boxed{ x=2y^{2}-1 }$

(c) We would like to eliminate $A$ from each pair of equations
$color{#4257b2}x=cos 2A, y=csc A$ to find an equation that relates $x$ to $y$. First, we note that $color{#4257b2}x=cos 2A$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2A=1-2sin^{2}A$.

$$
x=cos 2A
$$

$$
x=1-2sin^{2}A (3)
$$

But we know that $color{#4257b2}sin A=dfrac{1}{csc A}$, so we can replace $color{#4257b2}sin^{2}A$ from equation $(3)$ by $color{#4257b2}dfrac{1}{csc^{2}A}$.

$$
x=1-2sin^{2}A
$$

$$
x=1-dfrac{2}{csc^{2}A} (4)
$$

Now we note that $color{#4257b2}x$ is a function of $color{#4257b2}csc A$ and we know that $color{#4257b2}y=csc A$, so we can replace each $color{#4257b2}csc A$ from equation $(4)$ by $color{#4257b2}y$.

$$
x=1-dfrac{2}{csc^{2}A}
$$

$$
x=1-dfrac{2}{y^{2}}
$$

So the relation between $color{#4257b2}x$ and $color{#4257b2}y$ is $boxed{ x=1-dfrac{2}{y^{2}} }$

(d) We would like to eliminate $A$ from each pair of equations
$color{#4257b2}x=sin 2A, y=sec 4A$ to find an equation that relates $x$ to $y$. First, we note that $color{#4257b2}y=sec 4A$ but we know that $color{#4257b2}sec theta=dfrac{1}{cos theta}$, so we can replace $color{#4257b2}sec 4A$ form $y$ by $color{#4257b2}dfrac{1}{cos 4A}$.

$$
y=sec 4A
$$

$$
y=dfrac{1}{cos 4A}
$$

Now we note that $color{#4257b2}y$ contains $color{#4257b2}cos 4A$, so so we can use the double angle formula for the cosine function $color{#4257b2}cos 4A=1-2sin^{2}2A$.

$$
y=dfrac{1}{cos 4A}
$$

$$
y=dfrac{1}{1-2sin^{2}2A} (5)
$$

Now we note that $color{#4257b2}y$ is a function of $color{#4257b2}sin 2A$ and we know that $color{#4257b2}x=sin 2A$, so we can replace each $color{#4257b2}sin 2A$ from equation $(5)$ by $color{#4257b2}x$.

$$
y=dfrac{1}{1-2sin^{2}2A}
$$

$$
y=dfrac{1}{1-2x^{2}}
$$

So the relation between $color{#4257b2}x$ and $color{#4257b2}y$ is $boxed{ y=dfrac{1}{1-2x^{2}} }$

$$
text{color{#c34632}$(a) x=dfrac{2y}{1-y^{2}}$ $(b) x=2y^{2}-1$
\
\
$(c) x=1-dfrac{2}{y^{2}}$ $(d) y=dfrac{1}{1-2x^{2}}$}
$$

(a) We would like to solve the equation $color{#4257b2}cos 2x=sin x$ in the interval $color{#4257b2}0 leq x leq 2pi$. First, we note that the left side is $color{#4257b2}cos 2x$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2x=1-2sin^{2}x$.

$$
cos 2x=sin x
$$

$$
1-2sin^{2}x=sin x
$$

Now we can add $color{#4257b2}2sin^{2}-1$ to each side to make one side equals zero.

$$
1-2sin^{2}x+2sin^{2}x-1=sin x+2sin^{2}x-1
$$

$$
cancel{1}cancel{-2sin^{2}x}+cancel{2sin^{2}x}cancel{-1}=sin x+2sin^{2}x-1
$$

$$
2sin^{2}x+sin x-1=0
$$

Now we have quadratic equation, so we can factor to find the value of $color{#4257b2}sin x$.

$$
2sin^{2}x+sin x-1=0
$$

$$
left(sin x+1right)left(2sin x-1right)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}sin x$.

$$
sin x+1=0 text{or} 2sin x-1=0
$$

$$
sin x=-1 text{or} sin x=dfrac{1}{2}
$$

Now we have two cases for $color{#4257b2}sin x$, so we can solve each case to find the values of $color{#4257b2}x$.

For
$$
color{#4257b2}sin x=-1
$$

We can take $color{#4257b2}sin^{-1}$ fro each side.

$$
sin^{-1}left(sin xright)=sin^{-1}(-1)
$$

$$
x=sin^{-1}(-1)
$$

Note that $color{#4257b2}sin^{-1}left(sin thetaright)=theta$

But we know that $color{#4257b2}sin dfrac{3pi}{2}=-1$, so $color{#4257b2}sin^{-1}(-1)=dfrac{3pi}{2}$ and we can find the value of $color{#4257b2}x$.

$$
x=sin^{-1}(-1)
$$

$$
boxed{ x=dfrac{3pi}{2} }
$$

For
$$
color{#4257b2}sin x=dfrac{1}{2}
$$

We can take $color{#4257b2}sin^{-1}$ fro each side.

$$
sin^{-1}left(sin xright)=sin^{-1}left(dfrac{1}{2}right)
$$

$$
x=sin^{-1}left(dfrac{1}{2}right)
$$

But we know that $color{#4257b2}sin x$ is positive in quadrant $1$ and quadrant $2$, so we can find the values of $color{#4257b2}x$ where the reference angle $color{#4257b2}dfrac{pi}{6}$.

$$
x=dfrac{pi}{6} text{or} x=pi-dfrac{pi}{6}
$$

$$
boxed{ x=dfrac{pi}{6} } text{or} boxed{ x=dfrac{5pi}{6} }
$$

So the set solution for the equation is $color{#4257b2}left{dfrac{pi}{6}, dfrac{5pi}{6}, dfrac{3pi}{2}right}$

(b) We would like to solve the equation $color{#4257b2}sin 2x-1=cos 2x$ in the interval $color{#4257b2}0 leq x leq 2pi$. First, we note that our equation contains $color{#4257b2}sin 2x$ and $color{#4257b2}cos 2x$, so we can use the double angle formulas for the sine and cosine functions $color{#4257b2}2sin xcos x$ and $color{#4257b2}cos 2x=2cos^{2}x-1$.

$$
sin 2x-1=cos 2x
$$

$$
2sin xcos x-1=2cos^{2}x-1
$$

Now we can add $color{#4257b2}1-2cos^{2}x$ to each side.

$$
2sin xcos x-1+1-2cos^{2}x=2cos^{2}x-1+1-2cos^{2}x
$$

$$
2sin xcos x-2cos^{2}x=0
$$

Now we have quadratic equation, so we can take $color{#4257b2}2cos x$ as a common factor.

$$
2sin xcos x-2cos^{2}x=0
$$

$$
2cos xleft(sin x-cos xright)=0
$$

Now we can use the zero-factor property to find the values of $color{#4257b2}x$ for each case.

$$
2cos x=0 text{or} sin x-cos x=0
$$

$$
cos x=0 text{or} sin x=cos x
$$

Now we have two cases, so we can solve each case to find the values of $color{#4257b2}x$.

For
$$
color{#4257b2}cos x=0
$$

We can take $color{#4257b2}cos^{-1}$ fro each side.

$$
cos^{-1}left(cos xright)=cos^{-1}(0)
$$

$$
x=cos^{-1}(0)
$$

Note that $color{#4257b2}cos^{-1}left(cos thetaright)=theta$

But we know that $color{#4257b2}cos dfrac{pi}{2}=cos dfrac{3pi}{2}=0$, so $color{#4257b2}cos^{-1}(0)$ has two solutions $color{#4257b2}dfrac{pi}{2}$ and $color{#4257b2}dfrac{3pi}{2}$ and we can find the value of $color{#4257b2}x$.

$$
x=cos^{-1}(0)
$$

$$
boxed{ x=dfrac{pi}{2} text{or} x=dfrac{3pi}{2} }
$$

For
$$
color{#4257b2}sin x=cos x
$$

We can divide the two sides by $color{#4257b2}cos x$.

$$
dfrac{sin x}{cos x}=dfrac{cos x}{cos x}
$$

$$
tan x=1
$$

Note that $color{#4257b2}tan x=dfrac{sin x}{cos x}$. Now we can take $color{#4257b2}tan^{-1}$ fro each side.

$$
tan^{-1}left(tan xright)=tan^{-1}left(1right)
$$

$$
x=tan^{-1}left(1right)
$$

But we know that $color{#4257b2}tan x$ is positive in quadrant $1$ and quadrant $3$, so we can find the values of $color{#4257b2}x$ where the reference angle $color{#4257b2}dfrac{pi}{4}$.

$$
x=dfrac{pi}{4} text{or} x=pi+dfrac{pi}{4}
$$

$$
boxed{ x=dfrac{pi}{4} } text{or} boxed{ x=dfrac{5pi}{4} }
$$

So the set solution for the equation is $color{#4257b2}left{dfrac{pi}{4}, dfrac{pi}{2}, dfrac{5pi}{4}, dfrac{3pi}{2}right}$

$$
text{color{#c34632}$(a) x=left{dfrac{pi}{6}, dfrac{5pi}{6}, dfrac{3pi}{2}right}$ $(b) x=left{dfrac{pi}{4}, dfrac{pi}{2}, dfrac{5pi}{4}, dfrac{3pi}{2}right}$}
$$

(a) We would like to express the function $color{#4257b2}sin 2theta$ in terms of $color{#4257b2}tan theta$. First, we note that our function is $color{#4257b2}sin 2theta$, so we can use the double angle formula for the sine function $color{#4257b2}sin 2theta=2sin thetacos theta$.

$$
sin 2theta=2sin thetacos theta (1)
$$

But we know that $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$, so we can result that $color{#4257b2}sin theta=tan thetacos theta$ and we can substitute this identity in equation $(1)$.

$$
sin 2theta=2sin thetacos theta
$$

$$
sin 2theta=2tan thetacos thetacos theta
$$

$$
sin 2theta=2tan thetacos^{2}theta
$$

But we know that $color{#4257b2}cos theta=dfrac{1}{sec theta}$, so we can replace $color{#4257b2}cos^{2}theta$ in our expression by $color{#4257b2}dfrac{1}{sec^{2}theta}$.

$$
sin 2theta=2tan thetacos^{2}theta
$$

$$
sin 2theta=dfrac{2tan theta}{sec^{2}theta}
$$

Now we can use the Pythagorean identity $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ to replace $color{#4257b2}sec^{2}theta$ from our expression by $color{#4257b2}1+tan^{2}theta$.

$$
sin 2theta=dfrac{2tan theta}{sec^{2}theta}
$$

$$
sin 2theta=dfrac{2tan theta}{1+tan^{2}theta}
$$

So we can express the function $color{#4257b2}sin 2theta$ as $boxed{ dfrac{2tan theta}{1+tan^{2}theta} }$

(b) We would like to express the function $color{#4257b2}cos 2theta$ in terms of $color{#4257b2}tan theta$. First, we note that our function is $color{#4257b2}cos 2theta$, so we can use the double angle formula for the cosine function $color{#4257b2}cos 2theta=2cos^{2}theta-1$.

$$
cos 2theta=2cos^{2}theta-1
$$

But we know that $color{#4257b2}cos theta=dfrac{1}{sec theta}$, so we can replace $color{#4257b2}cos^{2}theta$ in our expression by $color{#4257b2}dfrac{1}{sec^{2}theta}$.

$$
cos 2theta=2cos^{2}theta-1
$$

$$
cos 2theta=dfrac{2}{sec^{2}theta}-1
$$

Now we can use the Pythagorean identity $color{#4257b2}1+tan^{2}theta=sec^{2}theta$ to replace $color{#4257b2}sec^{2}theta$ from our expression by $color{#4257b2}1+tan^{2}theta$.

$$
cos 2theta=dfrac{2}{sec^{2}theta}-1
$$

$$
cos 2theta=dfrac{2}{1+tan^{2}theta}-1
$$

Now we can unify the denominators using the common denominator $color{#4257b2}1+tan^{2}theta$.

$$
cos 2theta=dfrac{2}{1+tan^{2}theta}-1
$$

$$
cos 2theta=dfrac{2-left(1+tan^{2}thetaright)}{1+tan^{2}theta}
$$

$$
cos 2theta=dfrac{2-1-tan^{2}theta}{1+tan^{2}theta}=dfrac{1-tan^{2}theta}{1+tan^{2}theta}
$$

So we can express the function $color{#4257b2}cos 2theta$ as $boxed{ dfrac{1-tan^{2}theta}{1+tan^{2}theta} }$

(c) We would like to express the function $color{#4257b2}dfrac{sin 2theta}{1+cos 2theta}$ in terms of $color{#4257b2}tan theta$. First, we note that our function is $color{#4257b2}dfrac{sin 2theta}{1+cos 2theta}$, so we can use the double angle formulas for the sine and cosine functions $color{#4257b2}sin 2theta=2sin thetacos theta$ and
$color{#4257b2}cos 2theta=2cos^{2}theta-1$.

$$
begin{align*}
dfrac{sin 2theta}{1+cos 2theta}&=dfrac{2sin thetacos theta}{1+2cos^{2}theta-1}
\ \
&=dfrac{2sin thetacos theta}{cancel{1}+2cos^{2}thetacancel{-1}} text{cancel $1$ with $-1$}
\ \
&=dfrac{2sin thetacos theta}{2cos^{2}theta}
\ \
&=dfrac{cancel{2}sin thetacancel{cos theta}}{cancel{2}cos^{cancel{2}}theta} text{cancel $color{#4257b2}2cos theta$}
\ \
&=dfrac{sin theta}{cos theta}
\ \
&=tan theta
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$

So we can express the function $color{#4257b2}dfrac{sin 2theta}{1+cos 2theta}$ as $boxed{ tan theta }$

(d) We would like to express the function $color{#4257b2}dfrac{1-cos 2theta}{sin 2theta}$ in terms of $color{#4257b2}tan theta$. First, we note that our function is $color{#4257b2}dfrac{1-cos 2theta}{sin 2theta}$, so we can use the double angle formulas for the sine and cosine functions $color{#4257b2}sin 2theta=2sin thetacos theta$ and $color{#4257b2}cos 2theta=1-2sin^{2}theta$.

$$
begin{align*}
dfrac{1-cos 2theta}{sin 2theta}&=dfrac{1-left(1-2sin^{2}thetaright)}{2sin thetacos theta}
\ \
&=dfrac{1-1+2sin^{2}theta}{2sin thetacos theta} text{distribute the negative sign}
\ \
&=dfrac{cancel{1}cancel{-1}+2sin^{2}theta}{2sin thetacos theta}
text{cancel $1$ with $-1$}
\ \
&=dfrac{2sin^{2}theta}{2sin thetacos theta}
\ \
&=dfrac{cancel{2}sin^{cancel{2}}theta}{cancel{2sin theta}cos theta} text{cancel $color{#4257b2}2sin theta$}
\ \
&=dfrac{sin theta}{cos theta}
\ \
&=tan theta
end{align*}
$$

Note that in the final step we used the identity $color{#4257b2}tan theta=dfrac{sin theta}{cos theta}$

So we can express the function $color{#4257b2}dfrac{1-cos 2theta}{sin 2theta}$ as $boxed{ tan theta }$

$$
text{color{#c34632}$(a) dfrac{2tan theta}{1+tan^{2}theta}$ $(b) dfrac{1-tan^{2}theta}{1+tan^{2}theta}$ $(c) tan theta$ $(d) tan theta$}
$$