All Solutions
Page 369: Check Your Understanding
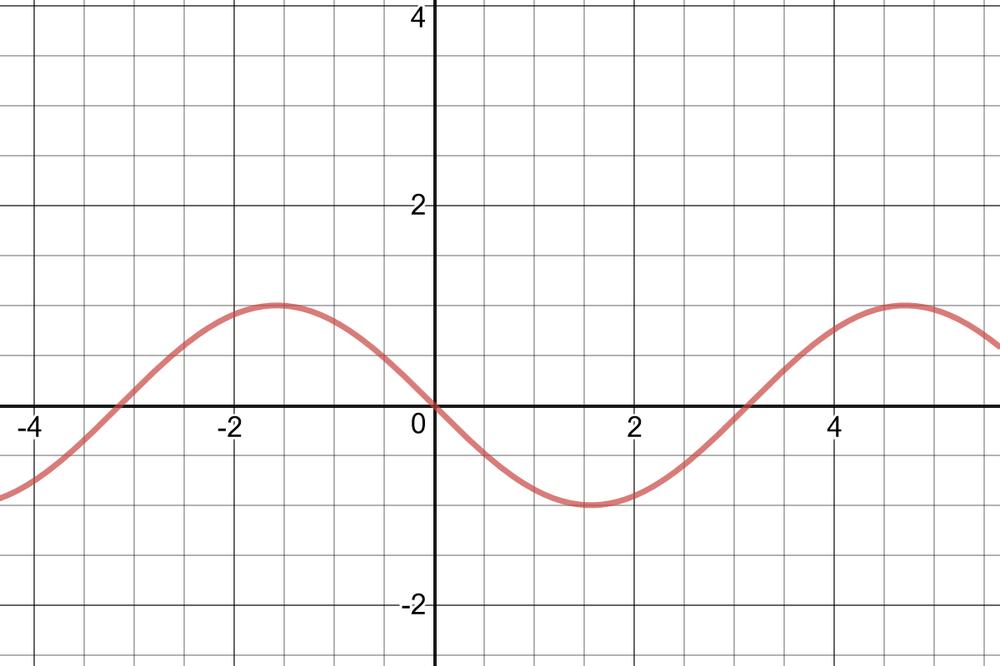
The average rate of change is zero in hte intervals of $0< x < pi, pi < x < 2pi$.
#### (b)
The average rate of change is negative in the intervals of $-dfrac{pi}{2} < x < dfrac{pi}{2}, dfrac{3pi}{2} < x <dfrac{5pi}{2}$.
#### (c)
The average rate of change is positive in the intervals of $dfrac{pi}{2} < x < dfrac{3pi}{2}, dfrac{5pi}{2} < x < 3pi$.
Two points where instantaneous rate of change is zero are $x=dfrac{pi}{4}, x=dfrac{5pi}{4}$.
#### (b)
Two points where the instantaneous rate of change is a negative value are $x=dfrac{pi}{2}, x=dfrac{5pi}{2}$.
#### (c)
Two points where the instantaneous rate of change is positive value are $x=0, x=2pi$
$left|dfrac{0-0}{5-2} right|=left|dfrac{0}{3} right|=0$
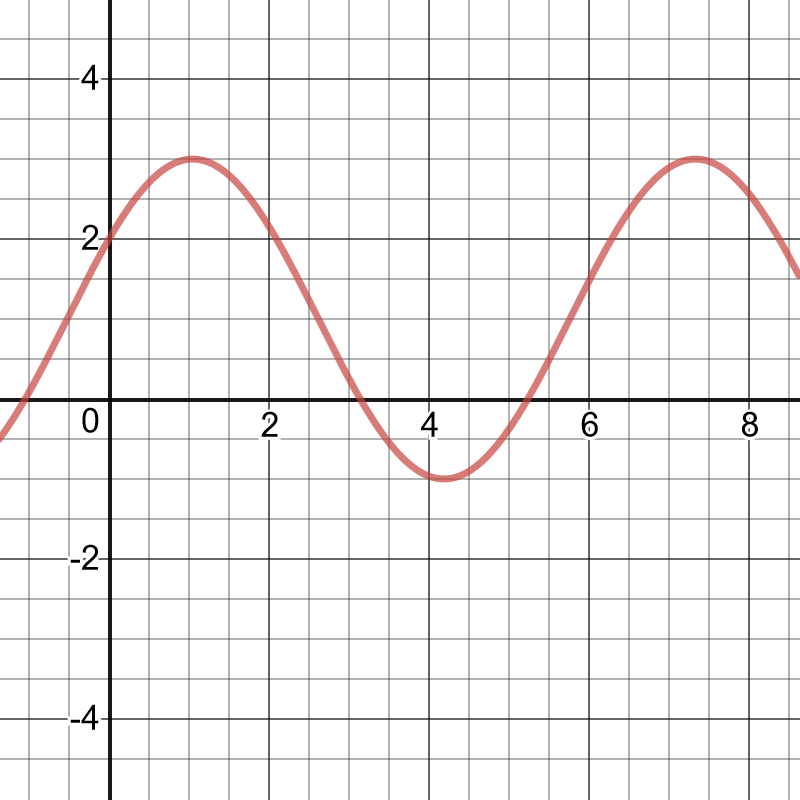
$0 leq x leq dfrac{pi}{2}$
Average rate of change$=dfrac{2.73-2}{dfrac{pi}{2}-0}=dfrac{0.73}{1.57}=0.465$
#### (b)
$dfrac{pi}{6}leq x leq dfrac{pi}{2}$
Average rate of chnage$=dfrac{2.73-2.73}{dfrac{pi}{2}-dfrac{pi}{6}}=dfrac{0}{1.047}=0$
#### (c)
$dfrac{pi}{3} leq x leq dfrac{pi}{2}$
Average rate of change$=dfrac{2.73-3}{dfrac{pi}{2}-dfrac{pi}{3}}=dfrac{-0.27}{0.5236}=-0.5157$
#### (d)
$dfrac{pi}{2} leq x leq dfrac{5pi}{4}$
Average rate of change$=dfrac{-0.932-2.73}{dfrac{5pi}{4}-dfrac{pi}{2}}=dfrac{-3.662}{2.356}=-1.554$
The average rate of change is zero in the intervals of $0 < x < dfrac{pi}{2}$, $pi < x < dfrac{3pi}{2}$.
#### (b)
The average rate of change is negative in the intervals of $0 < x < dfrac{pi}{4}, pi < x < dfrac{5pi}{4}$
#### (c)
The average rate of change is positive in the intervals of $dfrac{pi}{4} < x < dfrac{pi}{2}, dfrac{5pi}{4} < x <dfrac{3pi}{2}$.
Two points where the instantaneous rate of change is zero are $x=dfrac{1}{4}, x=dfrac{3}{4}$.
#### (b)
Two points where the instantaneous rate of change is a negative value are $x=0, x=1$.
#### (c)
Two points where the instantaneous rate of change is a positive value are $x=dfrac{1}{2}, x=dfrac{3}{2}$.
$y=6cos(3x)+2$ for $dfrac{pi}{4}leq x leq pi$
For $x=dfrac{pi}{4}$,
$y=6cos left( 3left(dfrac{pi}{4} right)right)+2$
$y=-2.2426$
For $x=pi$,
$y=6cos (3(pi))+2$
$y=-4$
Average rate of change$=dfrac{-2.2426-(-4)}{dfrac{pi}{4}-pi}=dfrac{1.7574}{-2.3562}=-0.7459$
#### (b)
$y=-5sinleft(dfrac{1}{2}x right)-9$ for $dfrac{pi}{4}leq x leq pi$
For $x=dfrac{pi}{4}$,
$y=-5sinleft(dfrac{1}{2}left( dfrac{pi}{4}right) right)-9$
$y=-10.9134$
For $x=pi$,
$y=-5sinleft(dfrac{1}{2}pi right)-9$
$y=-14$
Average rate of change$=dfrac{-10.9134-(-14)}{dfrac{pi}{4}-pi}=dfrac{3.0866}{-2.3562}=-1.310$
$y=dfrac{1}{4}cos(8x)+6$ for $dfrac{pi}{4} leq x leq pi$
For $x=dfrac{pi}{4}$,
$y=dfrac{1}{4}cosleft(8left( dfrac{pi}{4}right) right)+6$
$y=6.25$
For $x=pi$,
$y=dfrac{1}{4}cos (8pi)+6$
$6.25$
Average rate of change$=dfrac{6.25-6.25}{dfrac{0}{-2.3562}}=0$
Then the function that describes the height of the tip of the propeller is $h(t)=sin(400pi(t-dfrac{1}{800}))$.
The graph of this function is shown below.
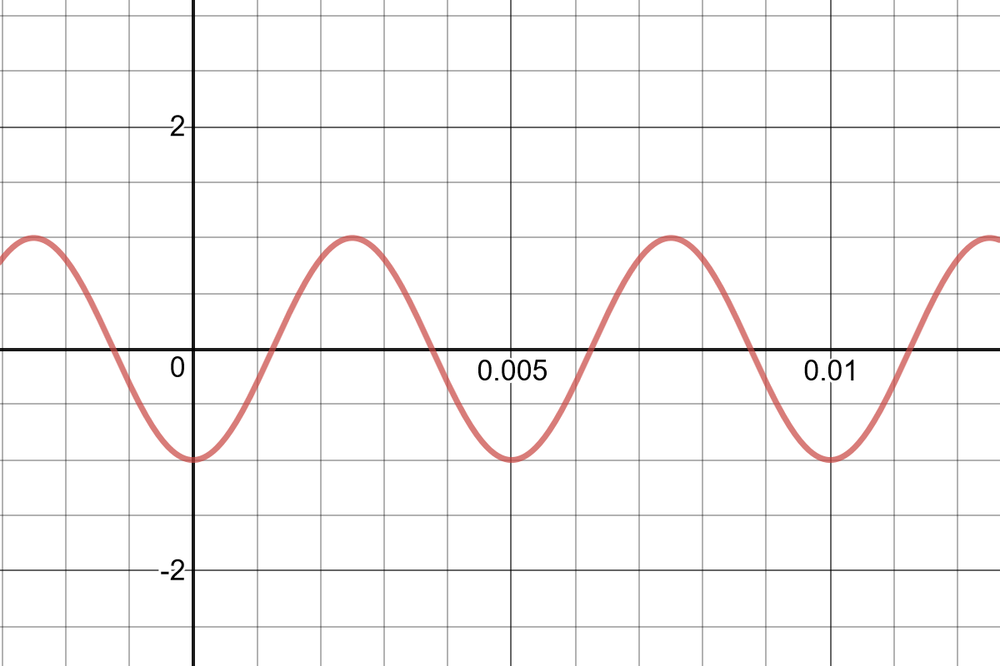
From the graph, it is clear that the instantaneous rate of change at $t=dfrac{1}{300}$ is negative.
The axis is at $20.2$.So, the equation of the axis is $y=20.2$ and the amplitude is $4.5$.
$k=dfrac{2pi}{24}=dfrac{pi}{12}$
$R(t)=4.5cosleft( dfrac{pi}{12}tright)+20.2$
#### (b)
fastest: $t=6 months, t=18 months, t=30 months, t=42 months$;
slowest: $t=0 months, t=12 months, t=24 months, t=36 months, t=48 months$
#### (c)
For $5leq tleq7$
$t=5$
$R(5)=4.5cosleft( dfrac{pi}{12}(5)right)+20.2$
$R(5)=21.364$
$t=7$
$R(7)=4.5cosleft(dfrac{pi}{12}(7) right)+20.2$
$R(7)=19.035$
Use the points $(5, 21.364)$ and $(7, 19.035)$.
$dfrac{19.035-21.364}{7-5}=dfrac{-2.329}{2}=-1.164$
$=1.164$ mice per owl/s
The instantaneous rate of change appears to be at its greatest at $12$ hours.
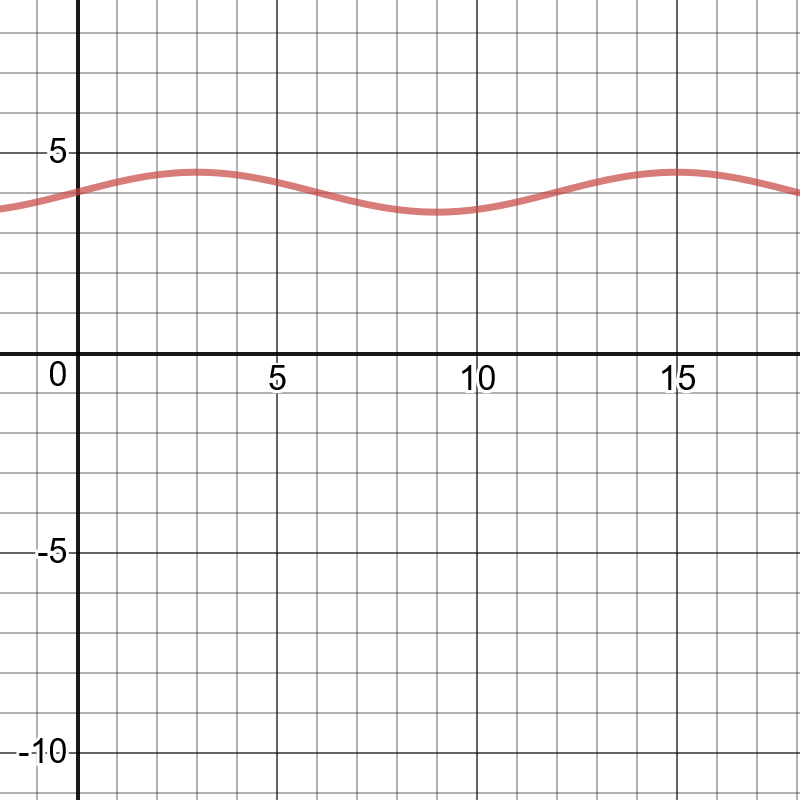
$t=11$
$y=0.5 sinleft(dfrac{pi}{6}(11) right)+4$
$y=3.75$
$t=13$
$y=0.5sinleft(dfrac{pi}{6}(13) right)+4$
$y=4.25$
Use the points $(11, 3.75)$ and $(13, 4.25)$.
$dfrac{4.25-3.75}{13-11}=dfrac{0.5}{2}=0.25 t/h$
ii) For $11.5leq t leq 12.5$
$t=11.5$
$y=0.5sinleft(dfrac{pi}{6}(11.5) right)+4$
$y=3.8706$
$t=12.5$
$y=0.5sinleft(dfrac{pi}{6}(12.5) right)+4$
$y=4.1294$
Use the points $(11.5, 3.8706)$ and $(12.5, 4.1294)$.
$dfrac{4.1294-3.8706}{12.5-11.5}=0.2588$ t/h
$t=11.75$
$y=0.5sinleft(dfrac{pi}{6} (11.75)right)+4$
$y=3.9347$
$t=12.25$
$y=0.5sinleft(dfrac{pi}{6}(12.25) right)+4$
$y=4.0653$
Use the points $(11.75, 3.9347)$ and $(12.25, 4.0653)$.
$dfrac{4.0653-3.9347}{12.25-11.75}=dfrac{0.1306}{0.5}=0.2612$ t/h
#### (b)
The estimate calculated in part iii) is most accurate. The smaller the interval, the more accurate the estimate.
Half od one cycle
#### (c)
$dfrac{-7.2-7.2}{1-0}=-14.4$ cm/s
#### (d)
The bob is moving the fastest when it passes throug its rest position. You can tell because the images of the balls are farthest apart at this point.
#### (e)
The pendulum’s rest poition is halfway between the maximum and minimum values on the graph.
Therefore, at this point, the pendulum’s instantaneous rate of change is at its maximum.
#### (a)
For $0leq t leq 5$,
$h(0)=sinleft(dfrac{pi}{5}(0) right)=0$
$h(5)=sinleft(dfrac{pi}{5}(5) right)=0$
$dfrac{0-0}{5-0}=0$
#### (b)
For $5.5 leq t leq 6.5$
$t=5.5$
$h(5.5)=sinleft(dfrac{pi}{5}(5.5) right)$
$h(5.5)=-0.309$
$h(6.5)=sinleft( dfrac{pi}{5}(6.5)right)$
$h(6.5)=-0.809$
Use the points $(5.5, -0.309)$ and $(6.5, -0.809)$.
$dfrac{-0.809-(-0.309)}{6.5-5.5}=dfrac{-0.5}{1}=-0.5$ m/s
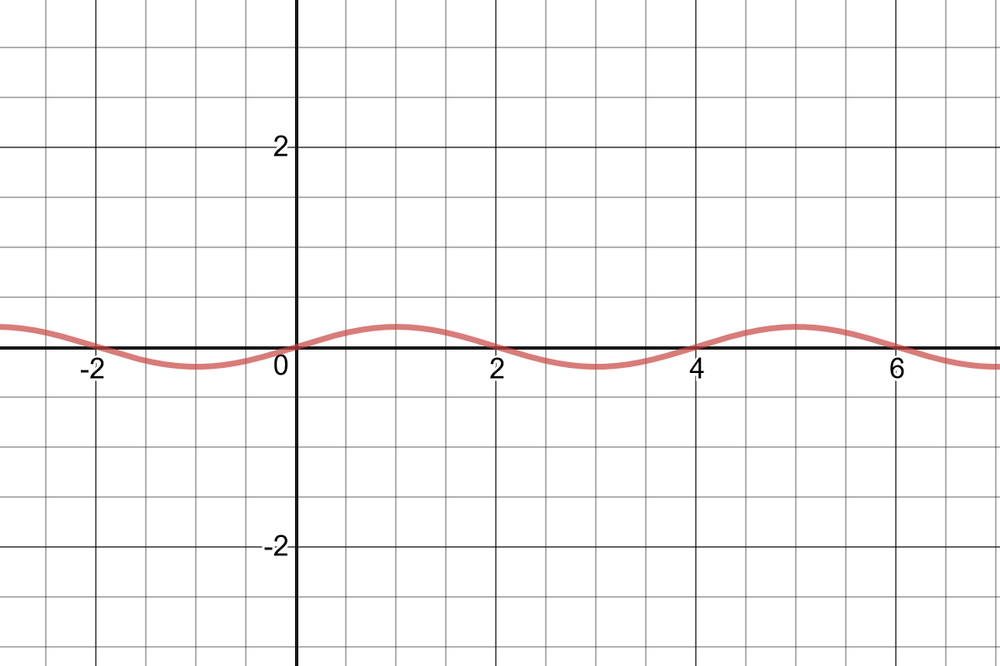
When $t=0, theta=0.$ When $t=1, theta=0.2$.The average rate of change is $0.2$ radians/s.
#### (c)
Answers may vary. For example, from the graph, it appears that the instantaneous rate of at $t=1.5$ is about $-dfrac{2}{3}$ radians/s.
#### (d)
The pendulum speed seems to be the greatest for $t=0, 2, 4, 6,$and $8$.
(The interval $-dfrac{pi}{4}< x <dfrac{pi}{4}$was used.)Therefore, the instantaneous rate of change of $f(x)=3sin x$is at its maximum tree times more than the instantaneous rate of change od $f(x)=sin x$.However, there are points where the instantaneous rate of change is the same for the two functions. For example, at $x=dfrac{pi}{2}$, it is $0$ for both functions.
By examining the graph of $f(x)=sin x$, it appears that the instantaneous rate of change at the given values of $x$ are $-1, 0, 1, 0,$ and $-1$.
The function is $f(x)=cos x$. Based on this information, the derivative of $f(x)=sin x$ is $cos x$.
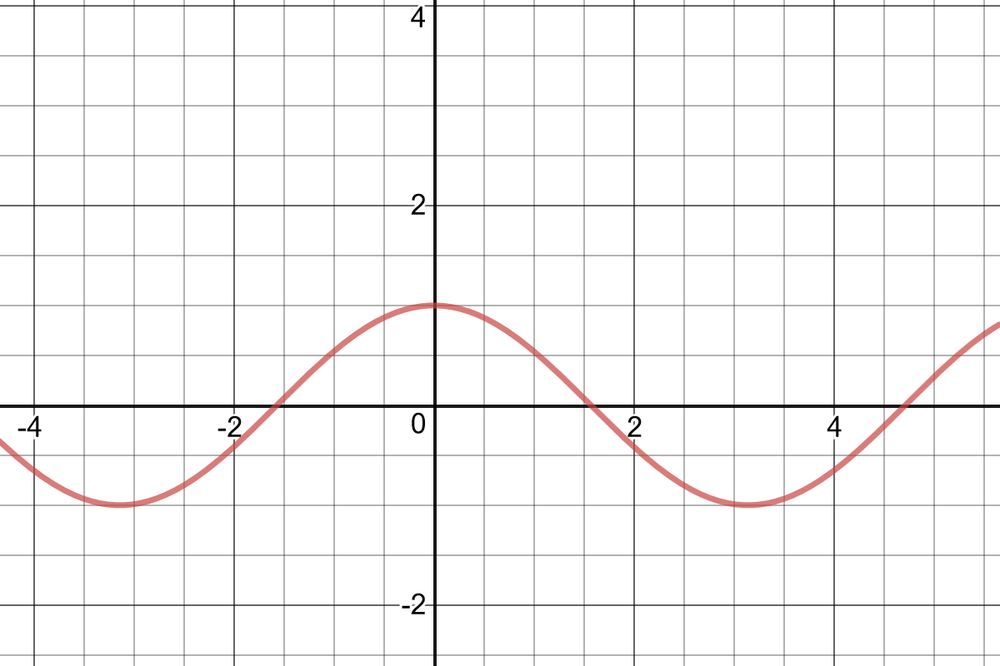
By examining the graph of $f(x)=cos x,$ it appears that the instantaneous rate of change at the given values of $x$ are $0, 1, 0, -1,$ and $0$.
#### (b)
The function is $f(x)=-sin x$. Based on this information, the derivative of $f(x)=cos x$ is $-sin x$.