$dfrac{cancel{pi}}{8}cancel{radians}timesleft(dfrac{180^{circ}}{cancel{pi radians}} right)=22.5^{circ}$

#### (b)

$4cancel{pi}cancel{radians}timesleft(dfrac{180^{circ}}{cancel{pi radians}} right)=720^{circ}$

#### (c)

$5cancel{radians}timesleft(dfrac{180^{circ}}{cancel{pi radians}} right)=286.5^{circ}$

#### (d)

$dfrac{11cancel{pi}}{12}cancel{radians}timesleft(dfrac{180^{circ}}{cancel{pi radians}} right)=165^{circ}$

$125^{circ}=125^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=2.2 radians$

#### (b)

$450^{circ}=450^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=7.9 radians$

#### (c)

$5^{circ}=5^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=0.1 radians$

#### (d)

$330^{circ}=330^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=5.8 radians$

#### (e)

$215^{circ}=215^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=3.8 radians$

#### (f)

$-140^{circ}=-140^{circ}timesleft(dfrac{pi radians}{180^{circ}} right)=-2.4 radians$

$10(2pi)=20pi$

#### (b)

$omega=dfrac{20pi}{5}=4pi radians/s$

#### (c)

Circumference$=2pi(19)=38pi$

$38pitimes10 revolutions=380pi$ cm

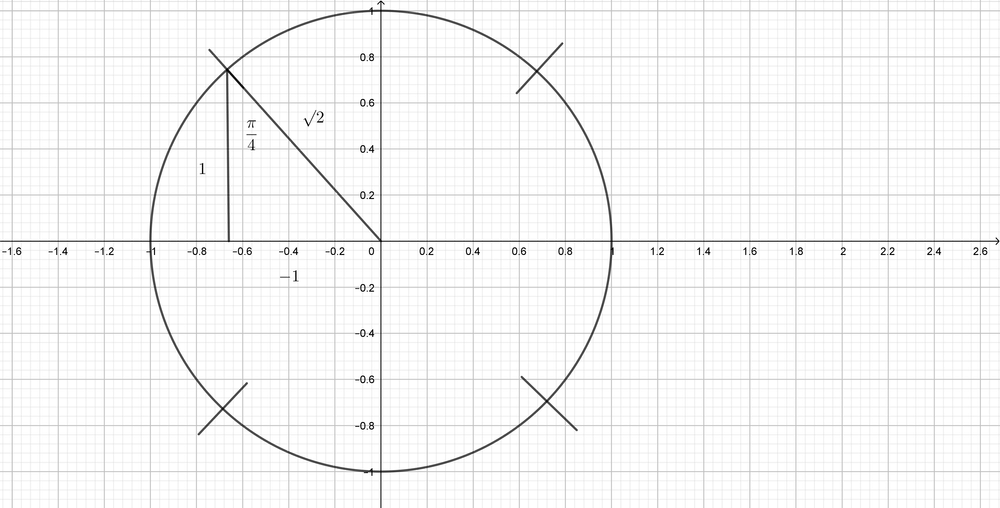
$$
sin dfrac{3pi}{4}=dfrac{1}{sqrt{2}}=dfrac{sqrt{2}}{2}
$$

$$
sin dfrac{11pi}{6}=-dfrac{1}{2}
$$

$$
tan dfrac{5pi}{3}=-sqrt{3}
$$

$$
tan dfrac{5pi}{6}=-dfrac{1}{sqrt{3}}=-dfrac{sqrt{3}}{3}
$$

$$
cos dfrac{3pi}{2}=dfrac{0}{1}=0
$$

$$
cos dfrac{4pi}{3}=-dfrac{1}{2}
$$

$(-3,14)=-1.360$

$tan^{-1}left(dfrac{14}{-3} right)=-1.360$

$theta=pi-1.360=1.78$

#### (b)

$(6,7)$ is in the first quadrant.

$tan^{-1}left( dfrac{7}{6}right)=0.86$

#### (c)

$(1,9)$ is in the first quadrant.

$tan^{-1}left(dfrac{9}{1} right)=1.46$

#### (d)

$(-5,-18)$ is in the third quadrant.

$tan^{-1}left(dfrac{-18}{-5} right)=1.30$

$theta=pi+1.30=4.44$

$(2,3)$ is in the first quadrant.

$tan^{-1}left(dfrac{3}{2} right)=0.98$

#### (f)

$(4,-20)$ is in the fourth quadrant.

$tan^{-1}left(dfrac{-20}{4} right)=-1.373$

$theta=2pi-1.360=4.91$

This is in the second quadrant where sine is positive.Sine is also positive in the first quadrant.
So, an equivalent expression would be $sindfrac{pi}{6}$.

#### (b)

This is in the fourth quadrant where cotangent is negative.Cotangent is also negative in the second quadrant.So, an equivalent expression would be $cotdfrac{3pi}{4}$.

#### (c)

Secant is undefined at $-dfrac{pi}{2}$. It is also undefined at $dfrac{pi}{2}$. So, an equivalent expression would be $sec dfrac{pi}{2}$.

#### (d)

This is in the third quadrant where cosine is negative. Cosine is also negative in the second quadrant.So, an equivalent expression would be $cosdfrac{5pi}{6}$
.

$x=0, pmpi, pm 2pi,…; y=0$

#### (b)

$x=pmdfrac{pi}{2}, pmdfrac{3pi}{2}, pmdfrac{5pi}{2},…; y=1$

#### (c)

$x=0, pmpi, pm 2pi,…; y=0$