#### (a)

period: $dfrac{2pi}{|k|}=dfrac{2pi}{|4|}=dfrac{pi}{2}$

amplitude: $|a|=|0.5|=0.5$

horizontal translation: $d=0$

equation of the axis: $y=0$

#### (b)

period: $dfrac{2pi}{|k|}=dfrac{2pi}{|1|}=2pi$

amplitude: $|a|=|1|=1$

horizontal tanslation: $d=dfrac{pi}{4}$

equation of the axis: $y=3$

#### (c)

period: $dfrac{2pi}{|k|}=dfrac{2pi}{3}$

amplitude: $|a|=|2|=2$

horizontal translation: $d=0$

equation of the axis: $y=-1$

#### (d)

period: $dfrac{2pi}{|k|}=dfrac{2pi}{|-2|}=pi$

amplitude: $|a|=|5|=5$

horizontal translation: $d=dfrac{pi}{6}$

equation of the axis: $y=-2$

For $y=0.5cos(4x)$

For $y=sinleft(x-dfrac{pi}{4} right)+3$

For $y=2sin(3x)-1$

For $y=5 cos left(-2x+dfrac{pi}{3} right)-2$

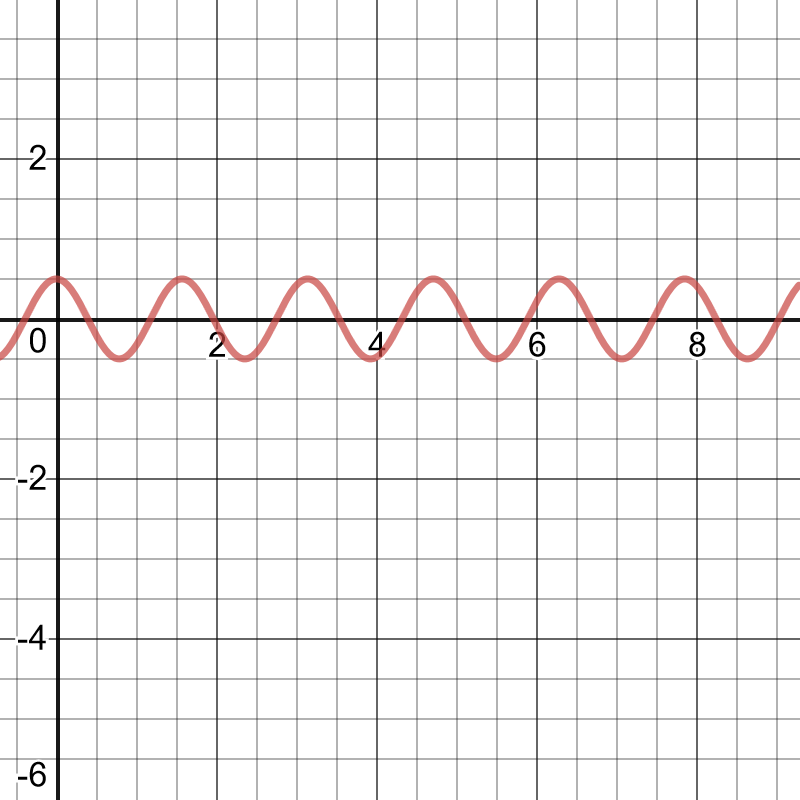
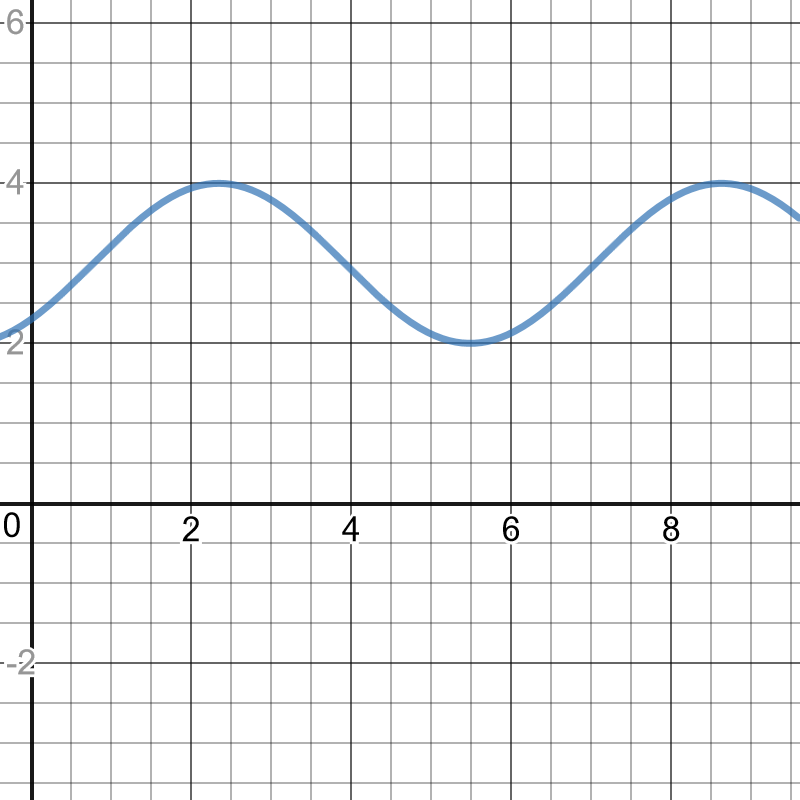
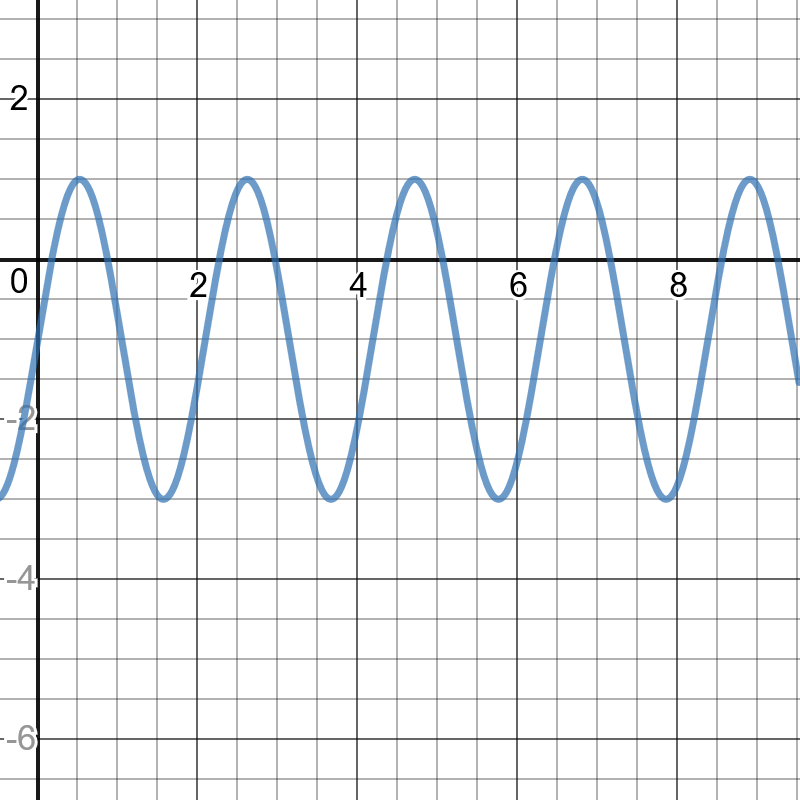
Only the last one is cut off.

$y=-2cosleft(4left(x+dfrac{pi}{4} right) right)+4$

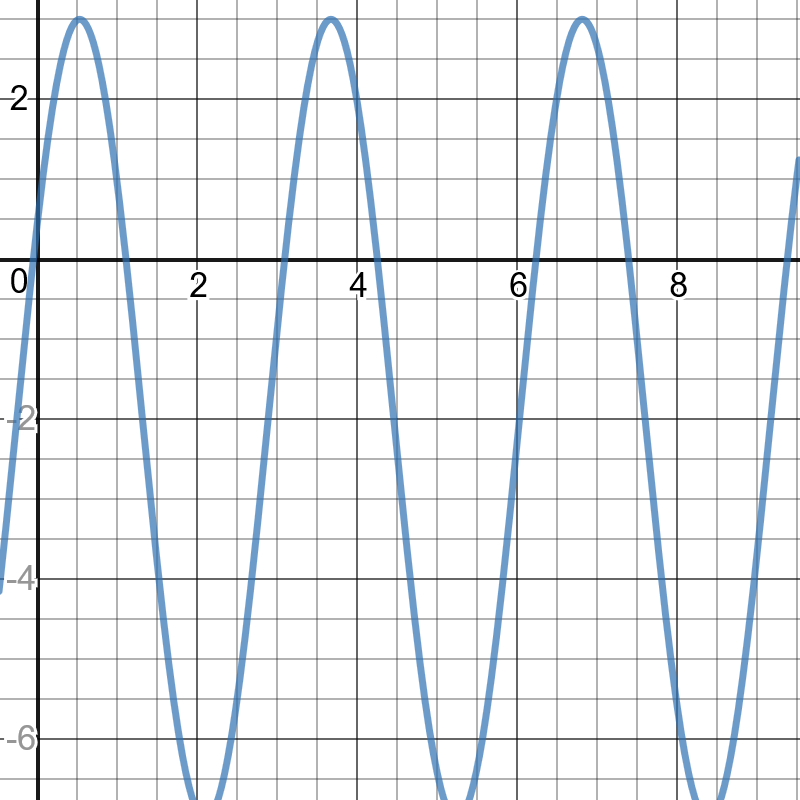
period: $dfrac{2pi}{|k|}=dfrac{2pi}{|4|}=dfrac{pi}{2}$

amplitude: $|a|=|-2|=2$

horizontal translation: $d=-dfrac{pi}{4}$ units to the left equation of the axis: $y=4$

$y=a sin (k(x-d))+c$

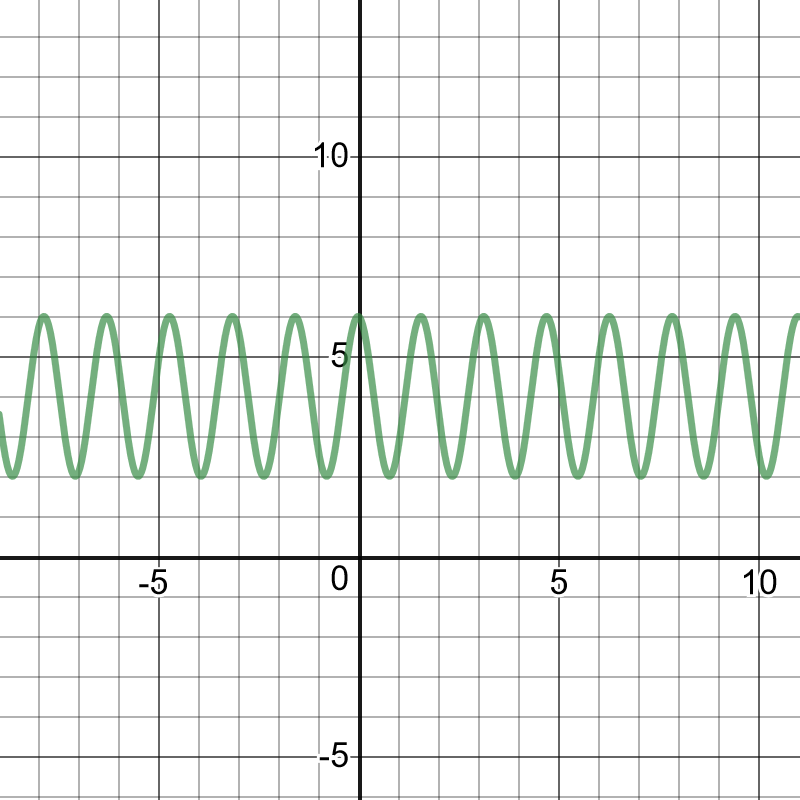
#### (a)

$a=25$

period: $dfrac{2pi}{|k|}=pi$

$k=2$

$f(x)=25 sin (2x)-4$

#### (b)

$a=dfrac{2}{5}$

period: $dfrac{2pi}{|k|}=10$

$k=dfrac{pi}{5}$

$f(x)=dfrac{2}{5}sinleft(dfrac{pi}{5}x right)+dfrac{1}{15}$

#### (c)

$$
a=80
$$

period: $dfrac{2pi}{|k|}=6pi$

$k=dfrac{1}{3}$

$f(x)=80 sinleft(dfrac{1}{3}x right)-dfrac{9}{10}$

#### (d)

$a=11$

period: $dfrac{2pi}{|k|}=dfrac{1}{2}$

$k=4pi$

$f(x)=11sin(4pi x)$

#### (a)

period$=2pi$, amplitude$=18$, equation of the axis is $y=0$; $y=18sin x$

#### (b)

period$=4pi$, amplitude$=6$, equation of the axis is $y=-2$; $y=-6sin(0.5x)-2$

#### (c)

period$=6pi$, amplitude$2.5$, equation of the axis is $y=6.5$;

$y=-2.5cosleft(dfrac{1}{3}x right)+6.5$

#### (d)

period$=4pi$, amplitude$=2$, equation of the axis is $y=-1$;

$y=-2cosleft(dfrac{1}{2}x right)-1$

#### (a)

$textbf{Vertical stretch}$ by a factor of $4$, $textbf{vertical translation}$ $3$ units up.

#### (b)

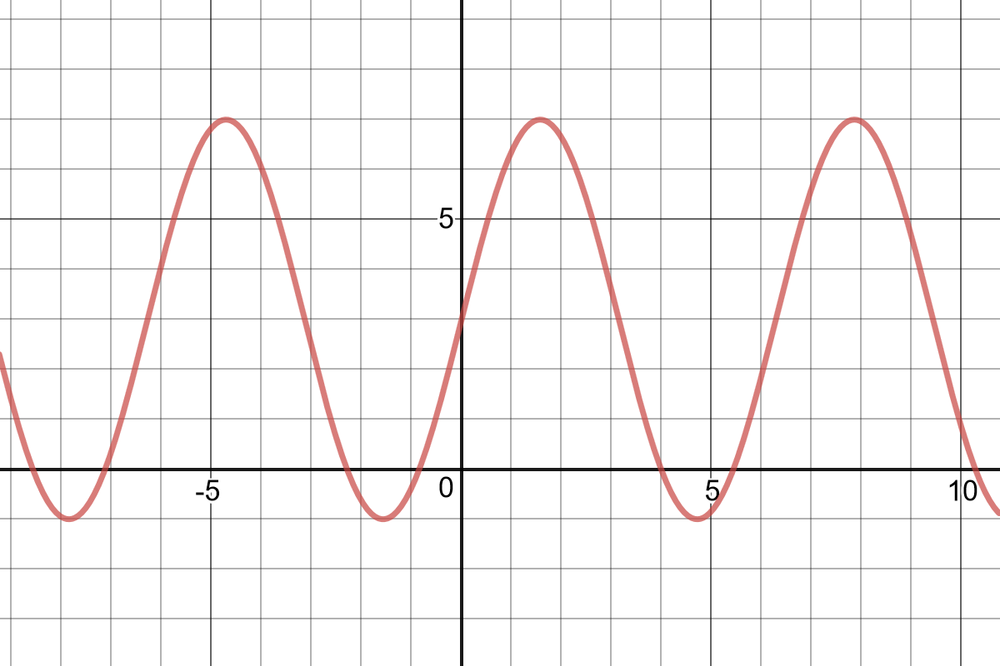
$textbf{Reflection}$ in the $x$-axis, $textbf{horizontal stretch}$ by a factor of $4$.

#### (c)

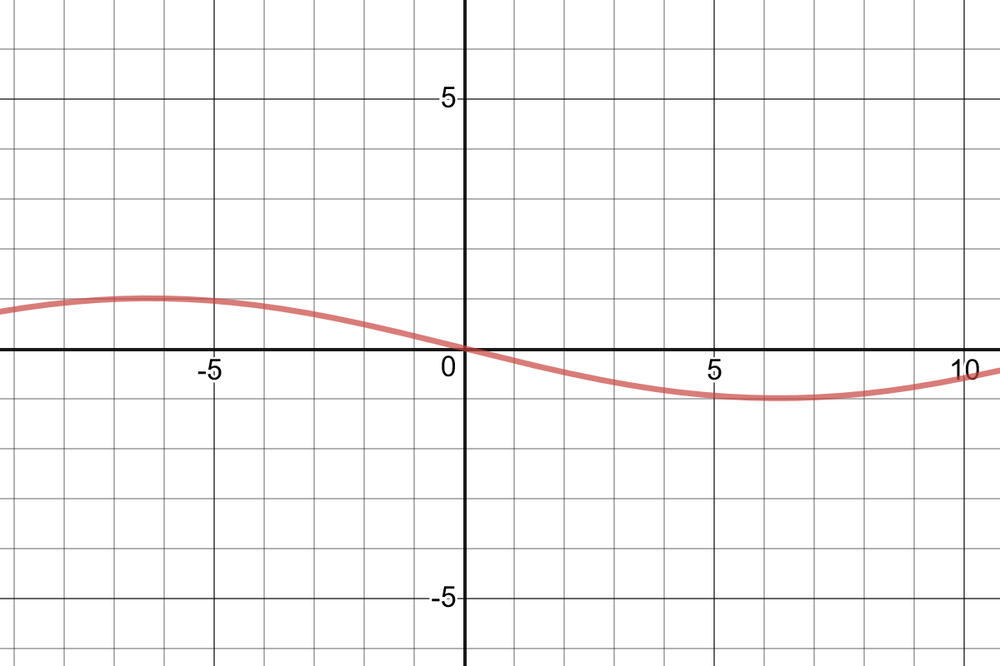
$textbf{Horizontal translation}$ $pi$ to the right, $textbf{vertical translation}$ $1$ unit down.

#### (d)

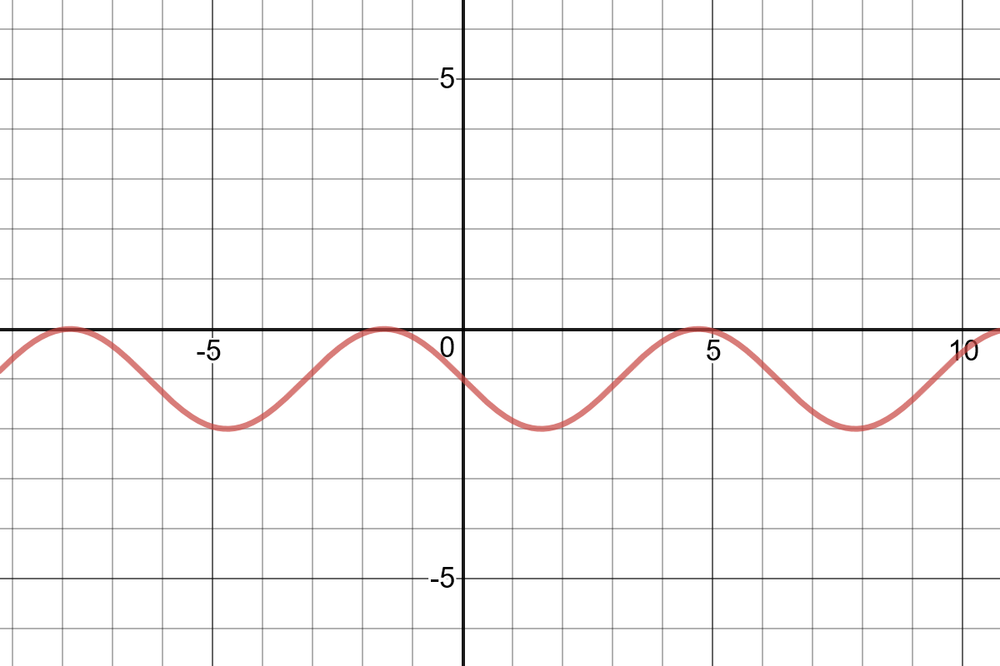
$textbf{Horizontal compression}$ by a factor of $dfrac{1}{4}$, $textbf{horizontal translation}$ $dfrac{pi}{6}$ to the left.

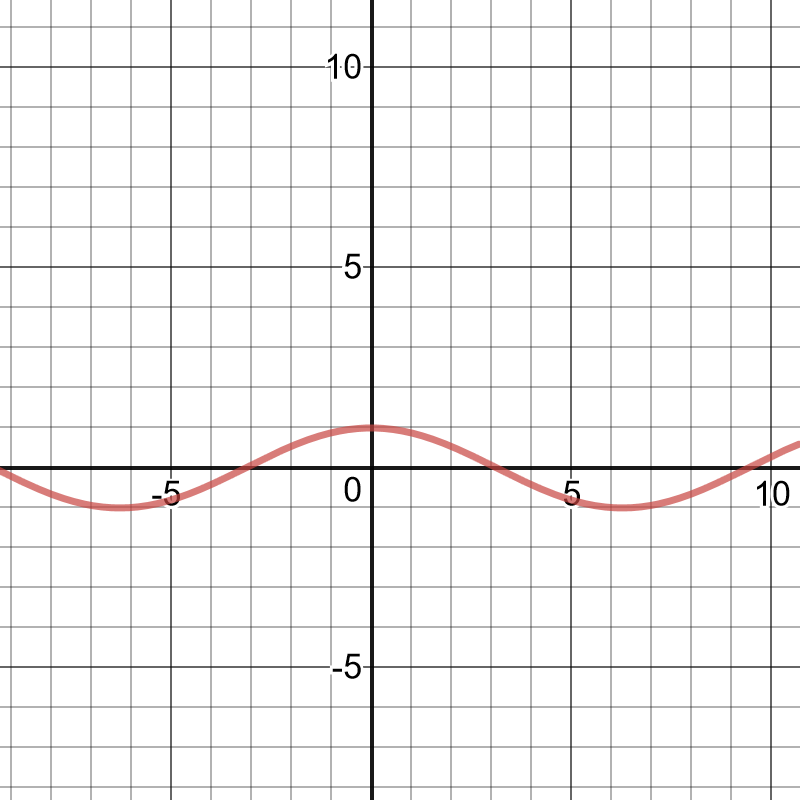
$$
f(x)=dfrac{1}{2}cos x+3
$$

$f(x)=cosleft(-dfrac{1}{2}x right)$

$f(x)=3cosleft(x-dfrac{pi}{2} right)$

$f(x)=cosleft(2left(x+dfrac{pi}{2} right) right)$

#### (a)

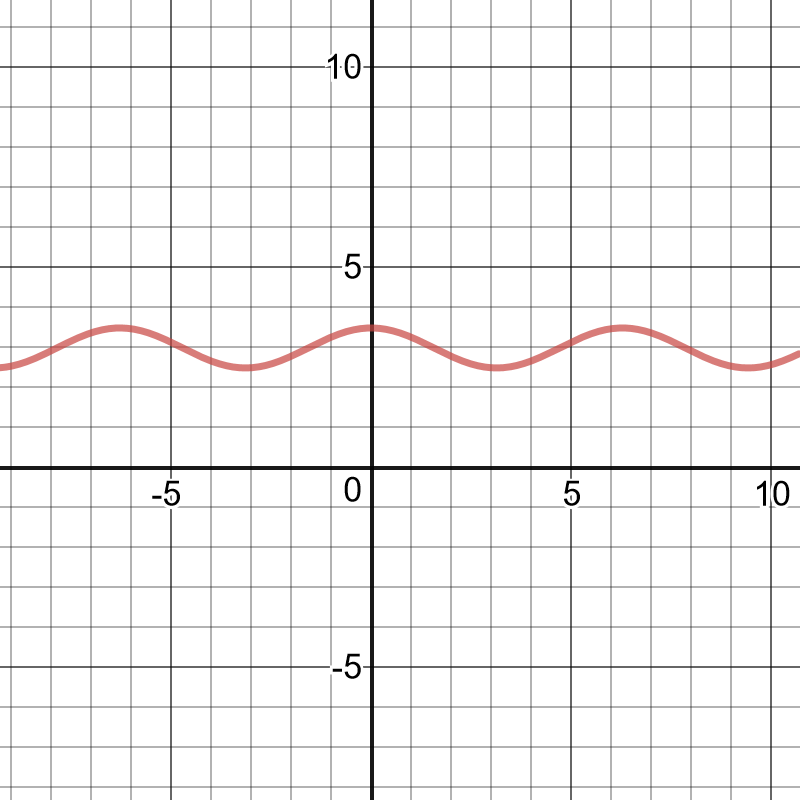
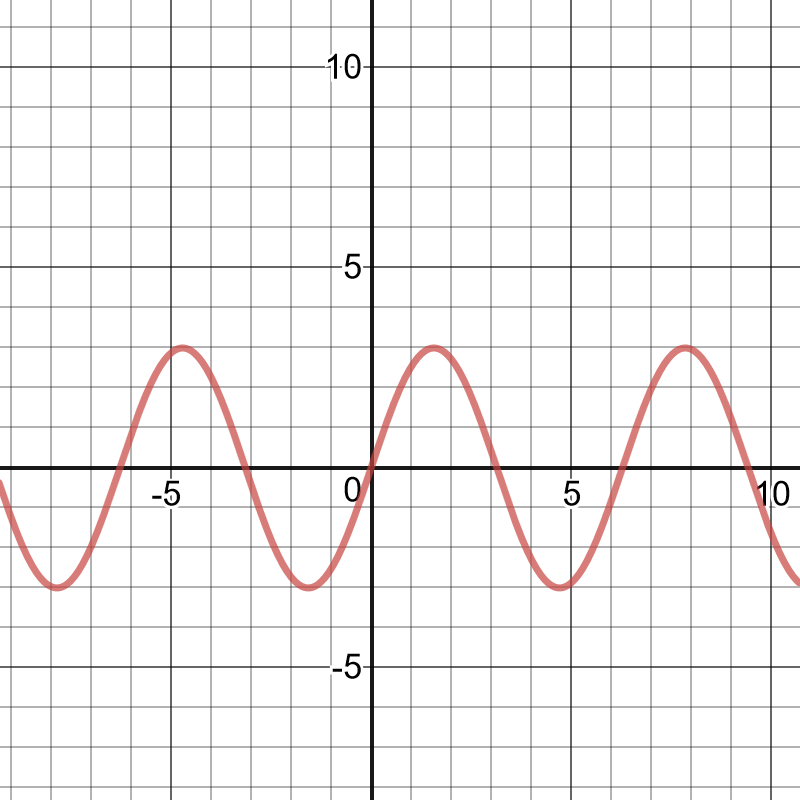
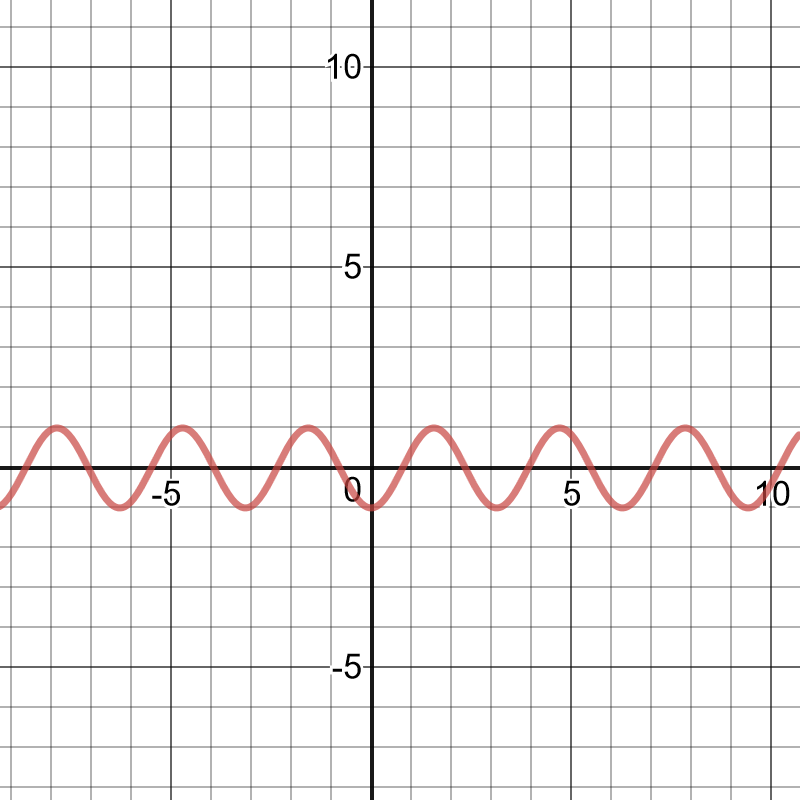
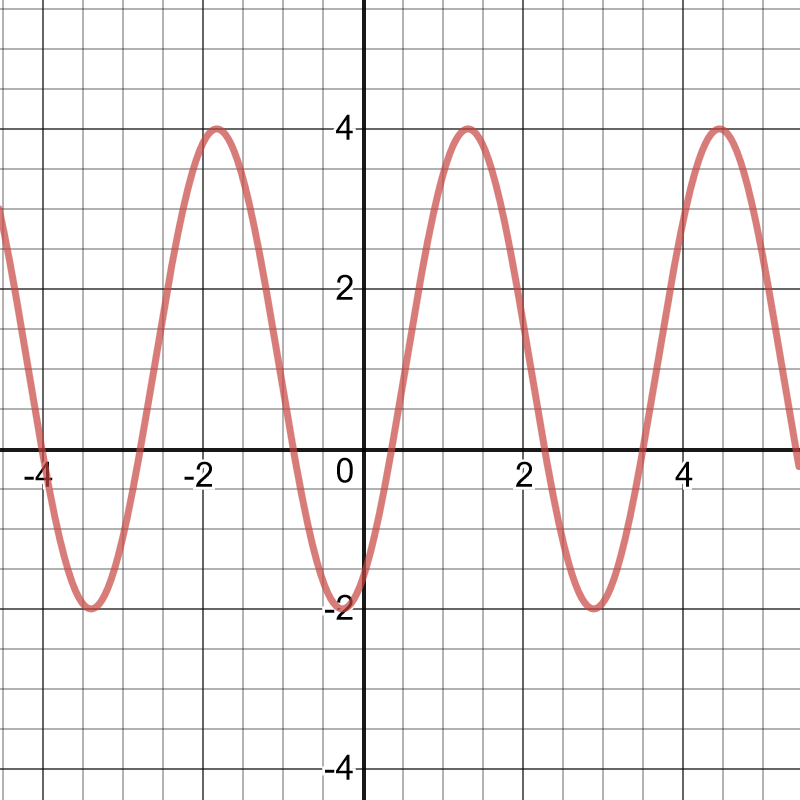
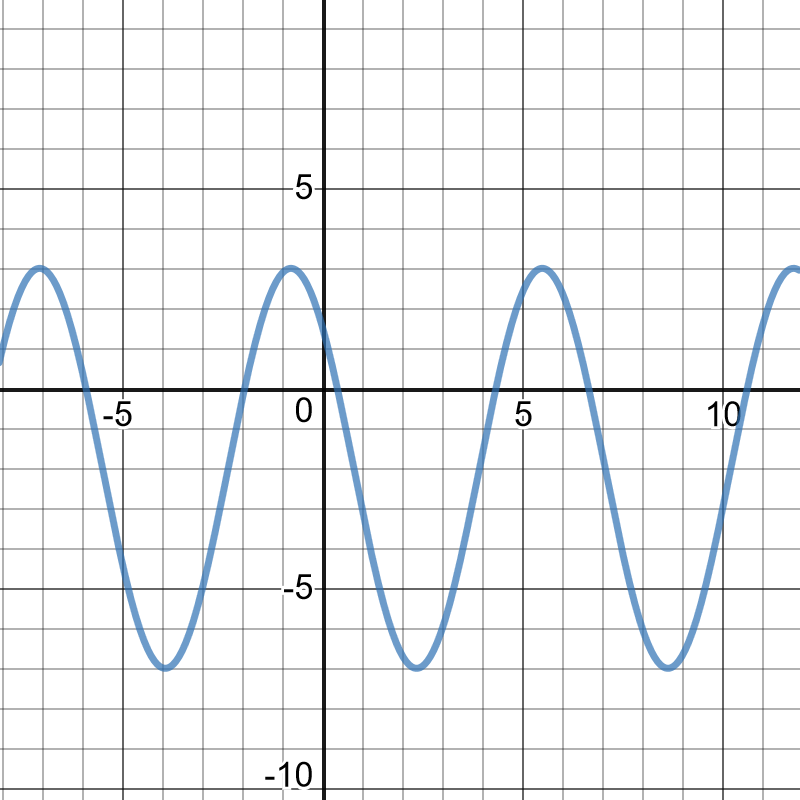
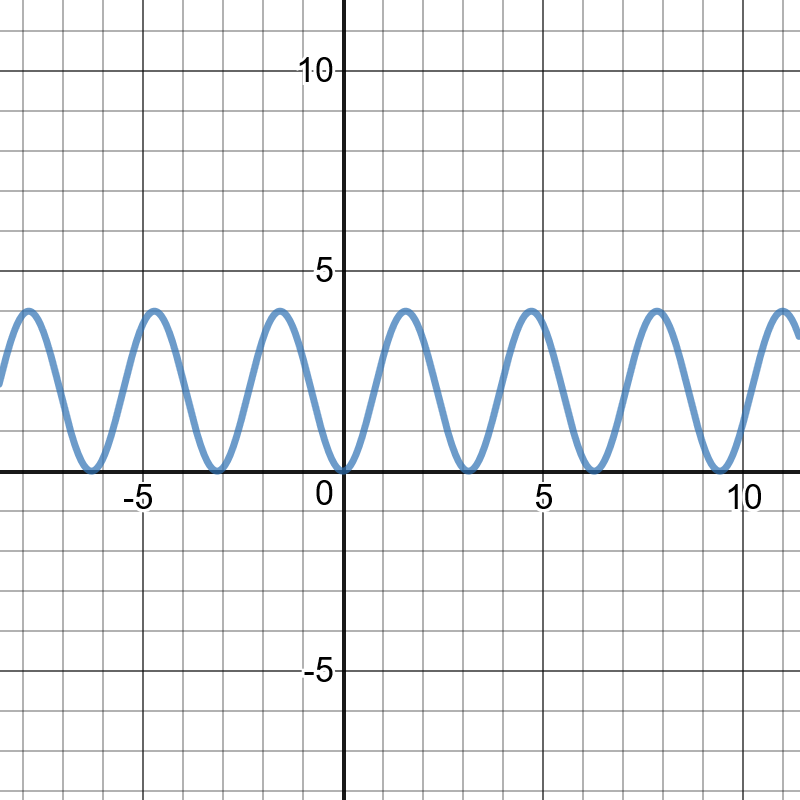
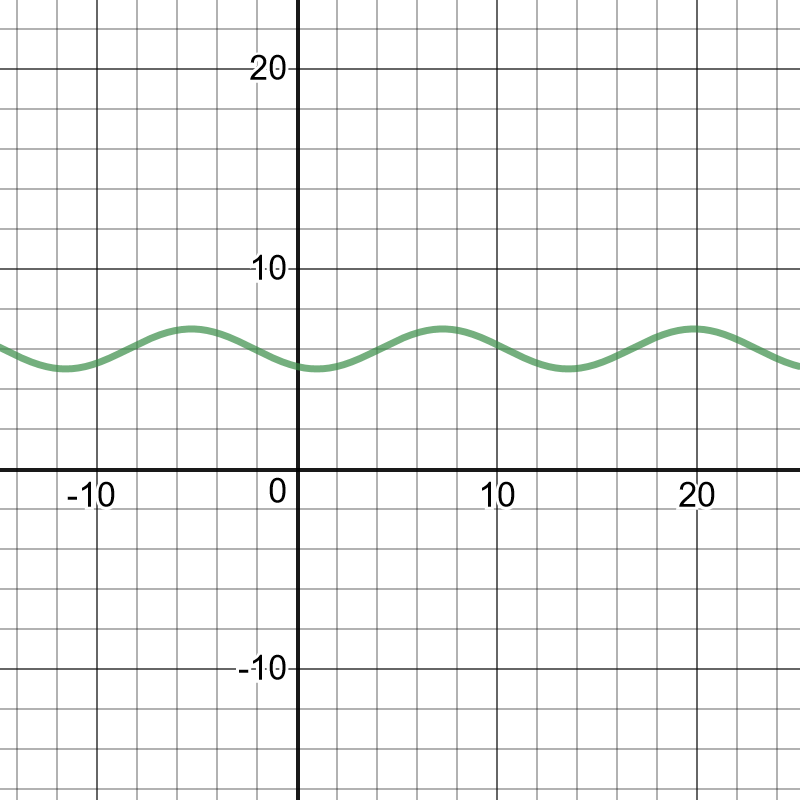
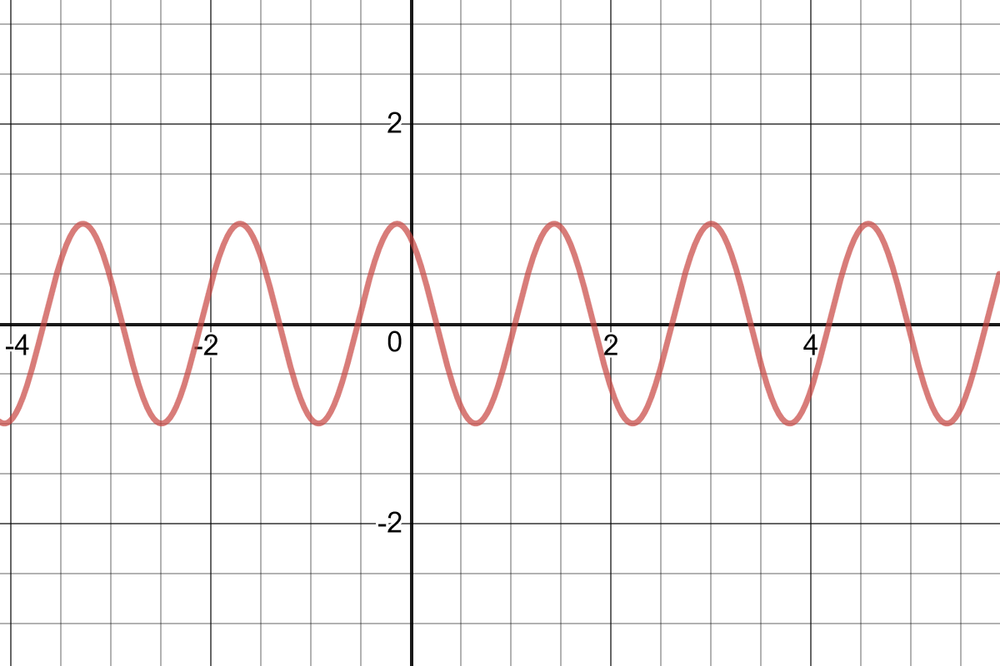
period:$dfrac{2pi}{|k|}=dfrac{5pi}{3}$

$k=dfrac{6}{5}$

The period of the function is $dfrac{6}{5}$.

This represents the time between one beat of a person’s heart and the next beat.

#### (b)

$P(60)=-20cosleft(dfrac{5pi}{3}(60) right)+100=80$

#### (d)

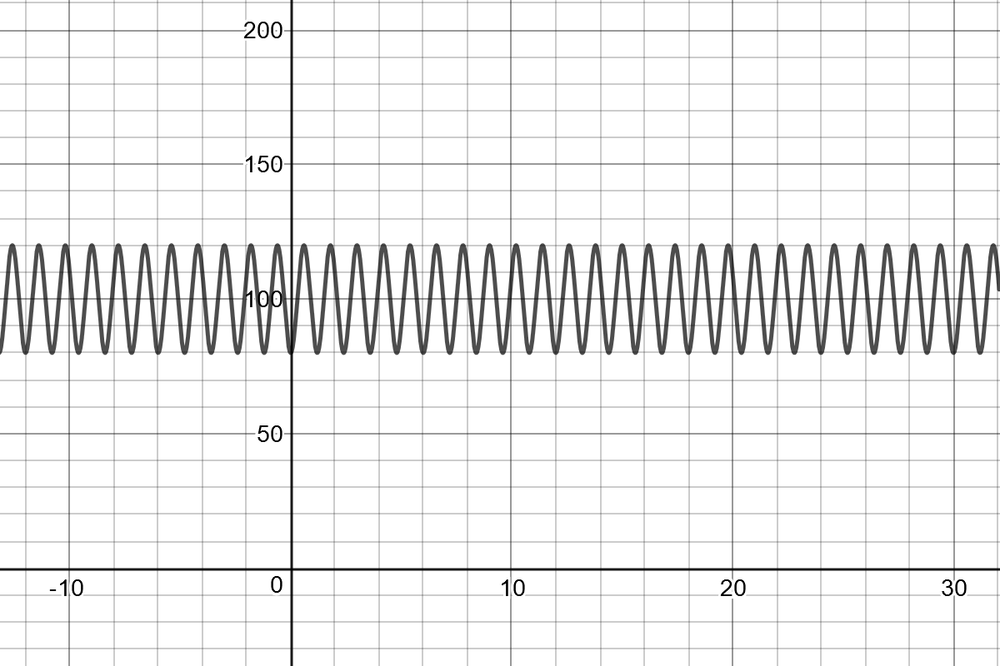
The range for the function is between $80$ and $120$. The range means the lowest blood pressure is $80$ and the highest blood pressure is $120$.

#### (b)

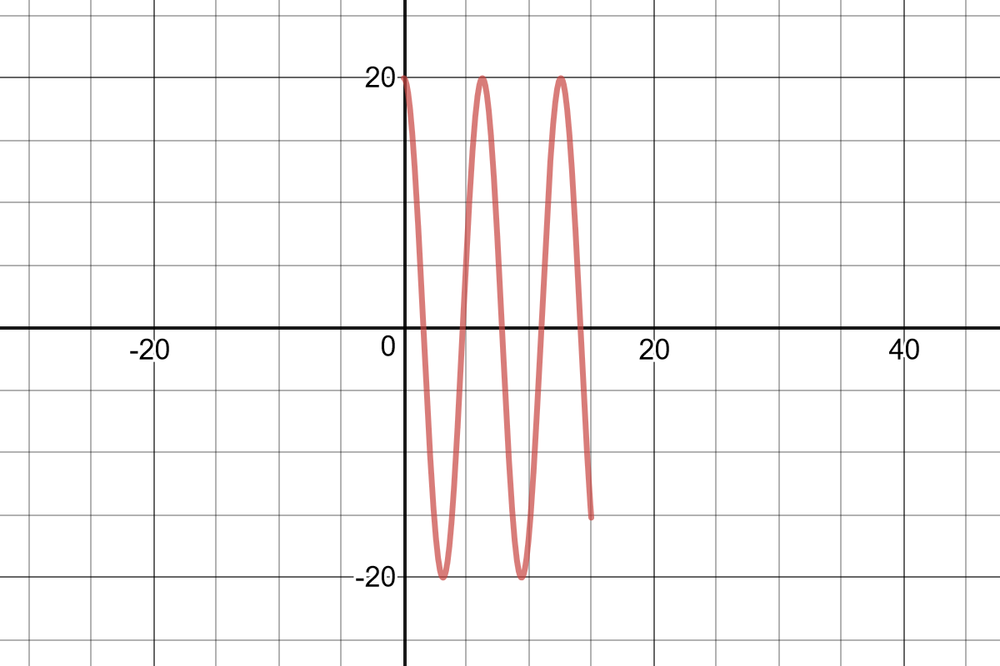
There is $textbf{a vertical stretch}$ by a factor of $20$. The period is $0.8$ s.

$dfrac{2pi}{k}=0.8$

$k=dfrac{5pi}{2}$

There is $textbf{a horizontal compression}$ by a factor of $dfrac{1}{|k|}=dfrac{2}{5pi}$.

There is $textbf{a horizontal translation}$ $0.2$ to the left.

#### (c)

$$
y=20sin(dfrac{5pi}{2}(x+0.2))
$$

#### (a)

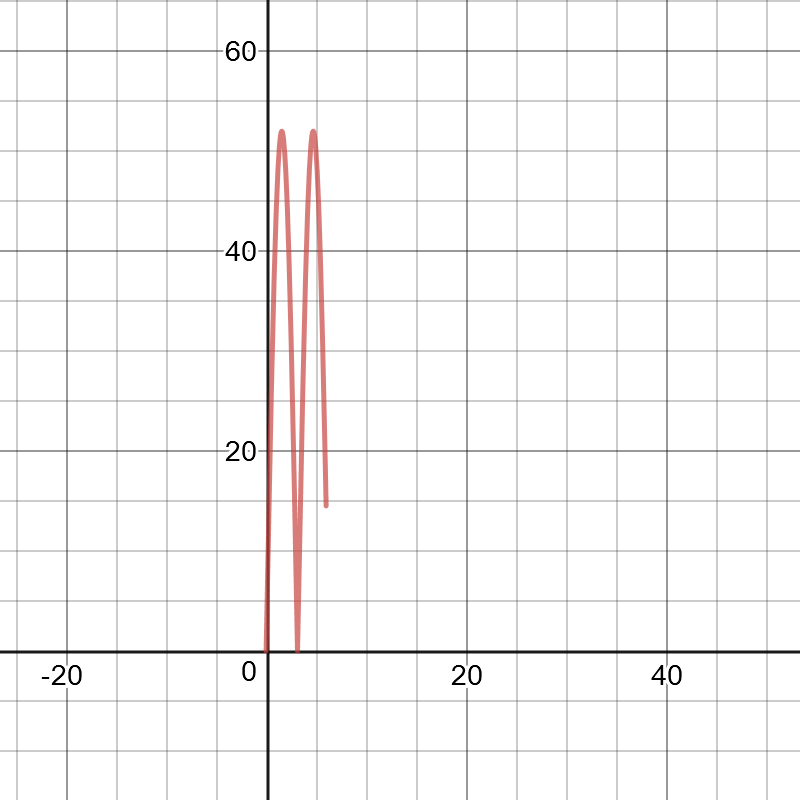
$textbf{Vertical stretch}$ by a factor of $25$, $textbf{reflection}$ in the $x$-axis, $textbf{vertical translation}$ $27$ units up, $textbf{the period}$ is $3$ s.

$dfrac{2pi}{k}=3$

$k=dfrac{2pi}{3}$

$textbf{horizontal compression}$ by a factor of $dfrac{1}{|k|}=dfrac{3}{2pi}$.
#### (c)

$y=-25cos(dfrac{2pi}{3}x)+27$

By looking at the difference in the $x$-values of the two maximums, $-dfrac{5pi}{7}$ and $-dfrac{3pi}{7}$, we see that the period is $dfrac{2pi}{7}$.

Answers may vary. For example, $left( dfrac{14pi}{13},5right)$.
Since the maximum is $4$ units above $y=9$, the minimum would be at $y=5$.If the period of the function is $2pi$, then the minimum would be at $dfrac{pi}{13}+pi$ of $dfrac{14pi}{13}$.

#### (a)

This isa cosine function with amplitude$=1$.

period$=dfrac{2pi}{0.5}=4pi$

$y=cos(4pi x)$

#### (b)

This issine function with a reflection in the $x$-axis and an amplitude$=2$.

period$=dfrac{2pi}{8}=dfrac{pi}{4}$

$$
y=-2sinleft( dfrac{pi}{4}xright)
$$

#### (c)

The $y$-axis is $y=-1$ and the amplitude is $4$.The function is shifted horizontally to the right by $10$.

period$=dfrac{2pi}{40}=dfrac{pi}{20}$

$y=4 sinleft(dfrac{pi}{20}(x-10) right)-1$

#### (a)

The car starts at the closest distance to the pole which is $100$ m.

#### (b)

The centre of the track is $400$ m from the pole because it is half the distance betwen the closest and furthest point.

#### (c)

The radius is $400-100=300$ m.

#### (d)

The period of the function is $80$ s.This is how long it takes to complete one lap.

#### (e)

$dfrac{2pi(300)}{80}m/s=23.56194$ m/s