
All Solutions
Page 314: Getting Started
$$
28^circ
$$
#### (b)
$3360^circ-28^circ=332^circ$
Side opposite: $-4$
Side adjacent: $3$
Hypotenuse: $h^2=3^2+4^2$
$h^2=25$
$h=5$
$sin theta=-dfrac{4}{5}$, $cos theta=dfrac{3}{5}$, $tan theta=-dfrac{4}{3}$,
$csctheta=-dfrac{5}{4}$, $sectheta=dfrac{5}{3}$, $cottheta=-dfrac{3}{4}$

$theta=sin^{-1}left(-dfrac{4}{5} right)$
$theta=307^{circ}$
The principal angle is $360^{circ}-53^{circ}=307^{circ}$
$sin60^{circ}=dfrac{sqrt{3}}{2}$
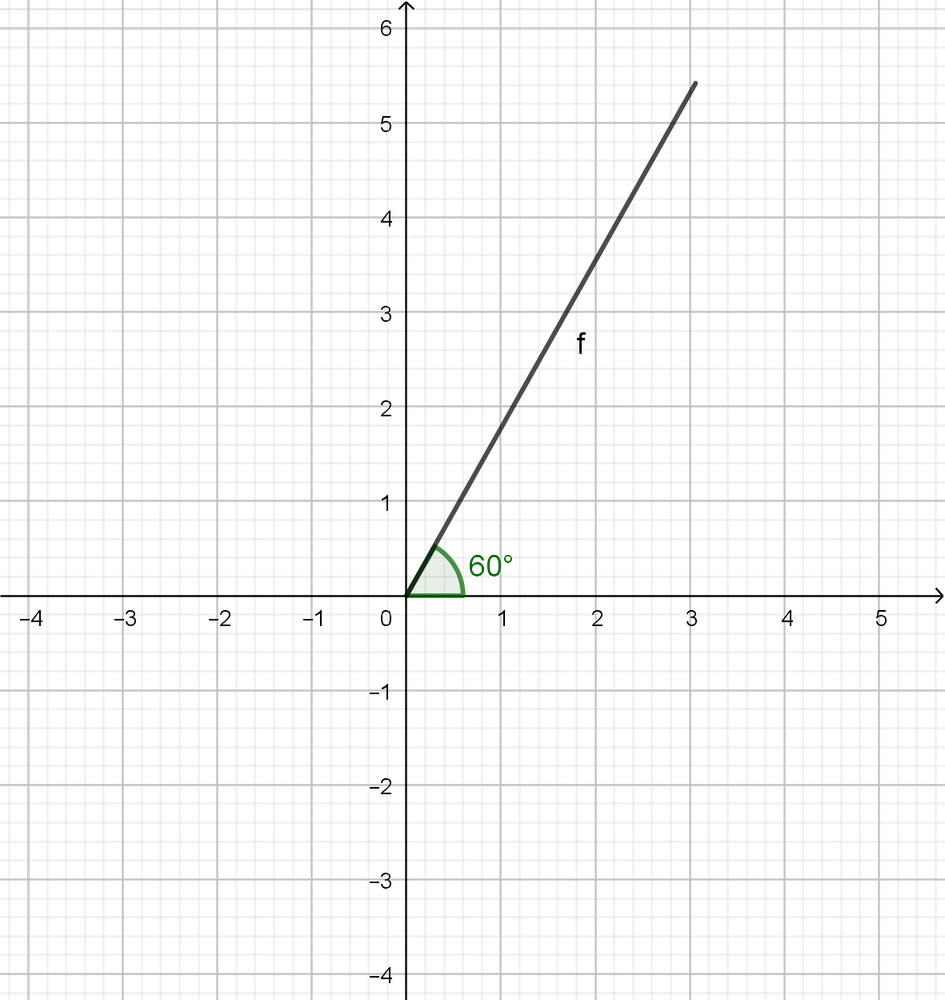
$tan 180^{circ}=dfrac{0}{1}=0$

$sin 120^{circ}=dfrac{sqrt{3}}{2}$

$cos 300^{circ}=dfrac{1}{2}$
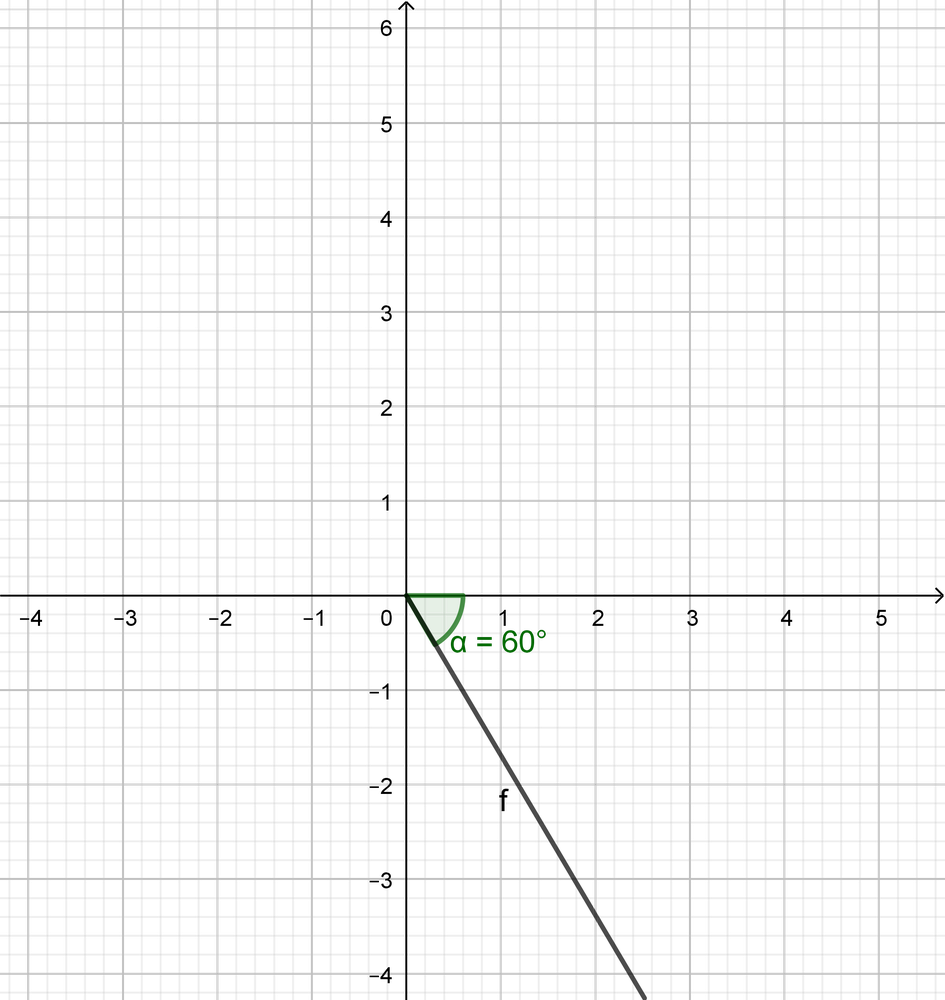
$sec 135^{circ}=-dfrac{sqrt{2}}{1}=-sqrt{2}$

$csc 270^{circ}=dfrac{1}{-1}=-1$

Since cosine is positive in the first and fourth quadrants, $theta=60^{circ}$,$300^{circ}$
#### (b)
Sincetangent is positive in the first and third quadrants, $theta=30^{circ}$,$210^{circ}$
#### (c)
Since tangent is positive in the first and third quadrants, $theta=45^{circ}$,$225^{circ}$
#### (d)
Cosine equals $-1$ at $theta=180^{circ}$
#### (e)
Contangent equals $-1$ at $theta=135^{circ}, 315^{circ}$
#### (f)
Sine equals $1$ at $theta=90^{circ}$
$$
textbf{Period=$360^circ$, amplitude=$1$, $y=0, R=left{yinBbb{R}|-1 leq y leq 1 right}$}
$$
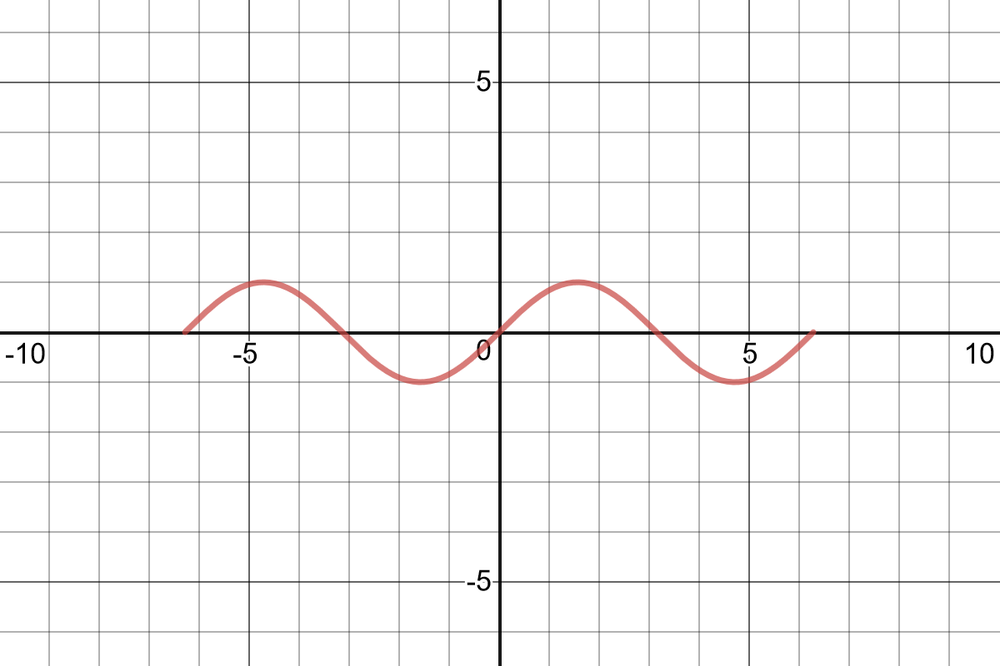
$$
textbf{Period=$360^circ$, amplitude=$1$, $y=0, R=left{yinBbb{R}| -1 leq y leq 1 right}$}
$$
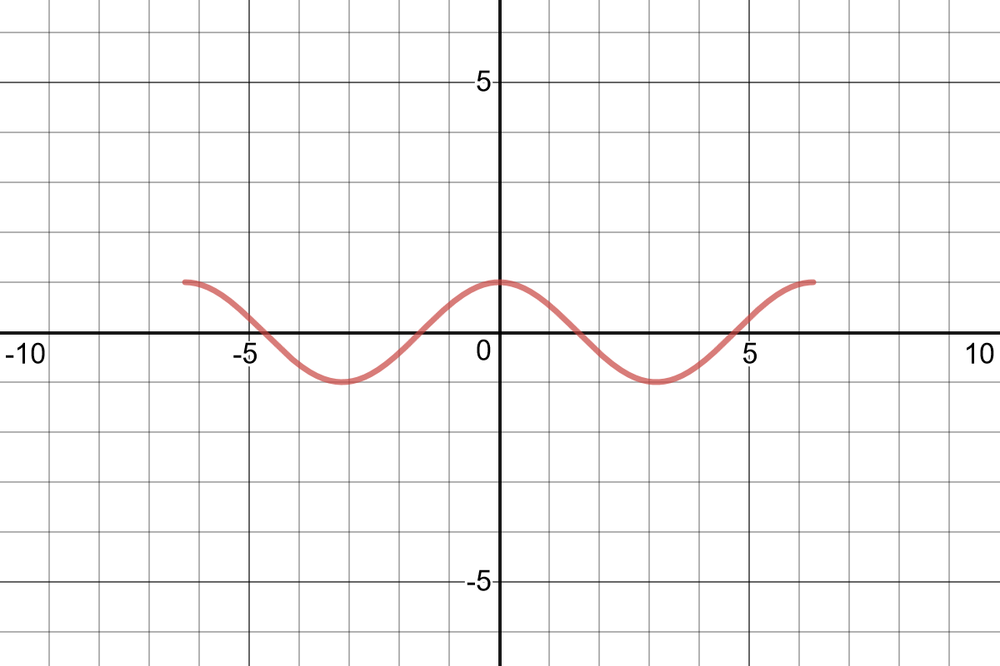
$textbf{period}$ = $dfrac{2cdot180}{3}=120$, $y=0$, $45^circ$ to the left, $textbf{amplitude}$=$2$.
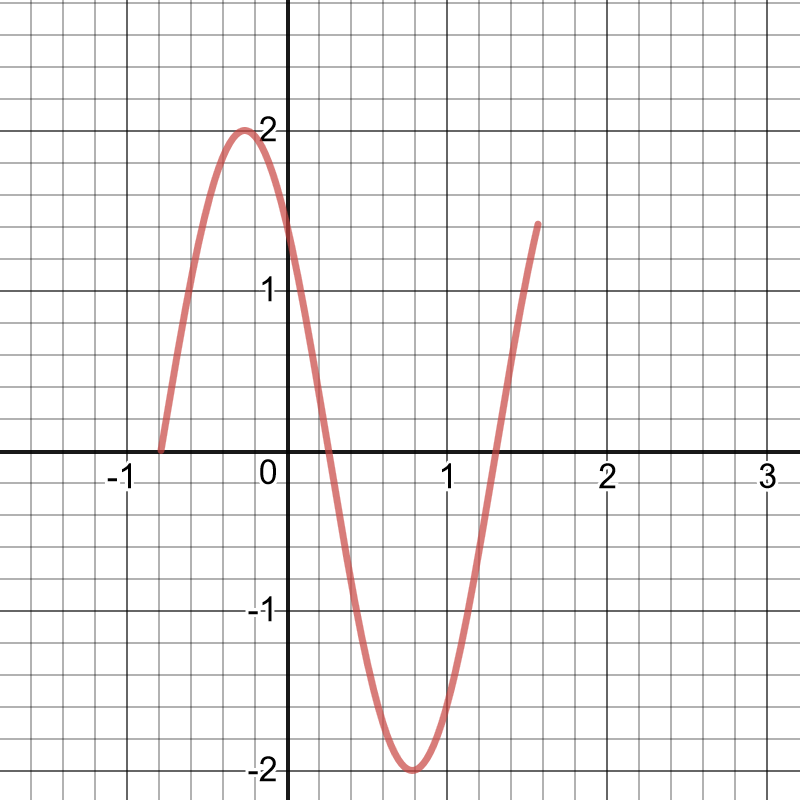
$textbf{period}$ = $dfrac{2cdot180}{dfrac{1}{2}}=720$, $y=-1$, $60^circ$ to the right, $textbf{amplitude}$=$1$.
Haven't found what you were looking for?
Search for samples, answers to your questions and flashcards

