The graph indicates that there is a vertical asymptote at $x=0.5$ and a horizontal asymptote at $y=0$. This matches equation B.

#### (b)

The graph indicates that there is a vertical asymptote at $x=1$ and a horizontal asymptote at $y=5$. This matches equation A.

(b) $x=1$; $y=5$

If $f(n)$ is very small (less than 1), then that would make $dfrac{1}{f(n)}$ a very small fraction.

#### (b)

If $f(n)$ is very small (less than 1), then that would make $dfrac{1}{f(n)}$ very large.

#### (c)

If $f(n)=0$, then that would make $dfrac{1}{f(n)}$ undefined at that point because you cannot divide by $0$.

#### (d)

If $f(n)$ is a positive, than that would make $dfrac{1}{f(n)}$ also positive because you are dividing two positive numbers.

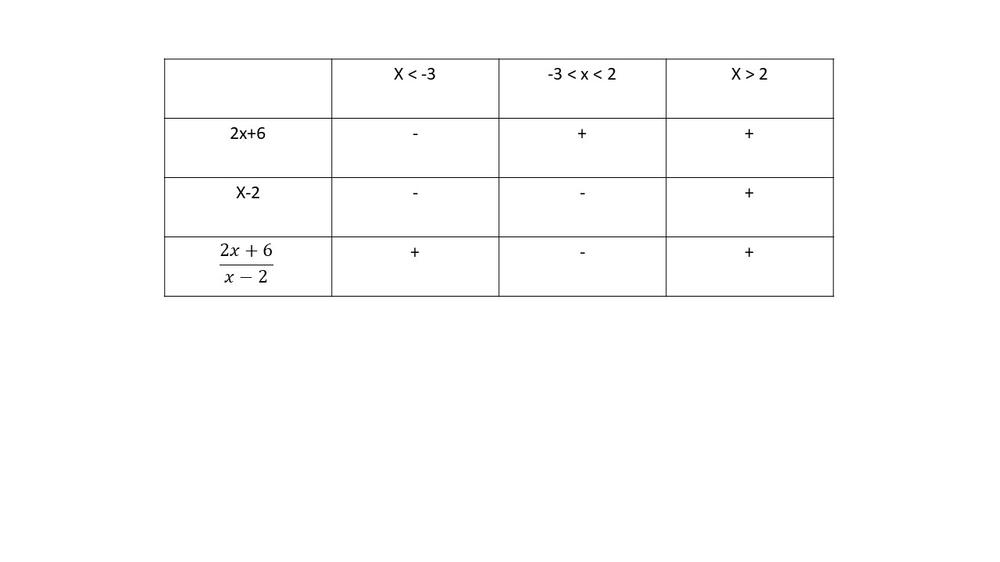
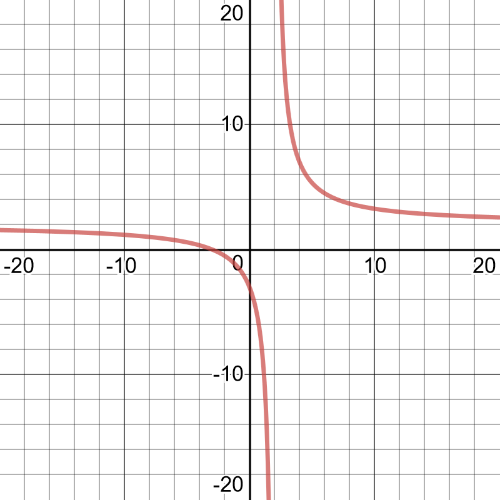
$0=x-2$

$2=x$

The horizontal asymptotes of the function can be found by dividing the first two terms of the expressions in the numerator and denominator.
$x$-intercept:

$0=dfrac{2x+6}{x-2}$

$0=2x+6$

$-6=2x$

$-3=x$

$y$-intercept:

$y=dfrac{2(0)+6}{0-2}=-3$

Use a table to determine when the graph is positive and negative.

$$
textbf{Because the expressin in the denominator is always increasing, this function will always be decreasing.}
$$

Use all of this information to sketch the graph.

be $dfrac{2249.52}{x}$.The company has made $2$$ profit on each pound of steel.So, the price of steel after it has been prpcessed would be$$dfrac{2249.52}{x}$+2$.The mass of the steel has lost$25$kilograms.The value of the steel would be the amount multiplied by the current price.$($dfrac{2249.52}{x}$+2)(x-25)=10838.52$\$(2249.52-2x)(x-25)=10838.52$\$2249.52x-56238+2x^2-50x=10838.52$\$2x^2-8639x-56238=0$\$x=4326$\

textbf{The original weight was}$4326$kg.\
textbf{The original cost would be $0.52$}$
$$
/kg.
$$

$textbf{The original cost would be $0.52$}$ $
$$
/kg.\
$$

We will use $textbf{algebraic}$ method.

$dfrac{-x}{x-1}=dfrac{-3}{x+7} / (x-1)(x+7)$

$-x(x+7)=-3(x-1)$

$-x^2-7x=-3x+3$

$x^2+4x+3=0$

$(x+1)(x+3)=0$

We can conclude that $textbf{solutions}$ are $x=-1$ and $x=-3$.

$dfrac{2}{x+5}>dfrac{3x}{x+10}$

$dfrac{2}{x+5}-dfrac{3x}{x+10}>0$

$(dfrac{x+10}{x+10})dfrac{2}{x+5}-(dfrac{x+5}{x+5})dfrac{3x}{x+10}>0$

$dfrac{2x+20}{(x+10)(x+5)}-dfrac{3x^2+15x}{(x+10)(x+5)}>0$

$dfrac{-3x^2-13x+20}{(x+10)(x+5)}>0$

$dfrac{(x+5.5)(x-1.2)}{(x+10)(x+5)}>0$

Frpm following table we can conclude that $textbf{this inequality is true on}$ $x<-10$, $-5.5<{x}1.2$.

(b) $x<-10$, $-5.5<{x}1.2$

To find $textbf{the vertical asymptotes}$ of the function, find the zeros of the expression in the denominator.

To find the equation of $textbf{the horizontal asymptotes}$ divide the first two terms of the expression in the numerator and denominator.
#### (b)

This type of function will have $textbf{a hole}$ when both the numerator and denominator share the same factor $(x+a)$.