#### (a)

This function will be a straight line and so, $textbf{the domain and range }$will be real numbers, $D=R=Bbb{R}$.

$textbf{$x$-intercept:}$

$0=3x+2$

$3x=-2$

$x=-dfrac{2}{3}$

$textbf{$y$-intercept:}$

$y=3cdot0+2$

$y=2$

The slope of the equation is positive abd so the function will always be $textbf{increasing}$.This means that the function will be $textbf{negative }$ on $(-infty,-dfrac{2}{3})$ and $textbf{positive}$ on $(-dfrac{2}{3},infty)$.
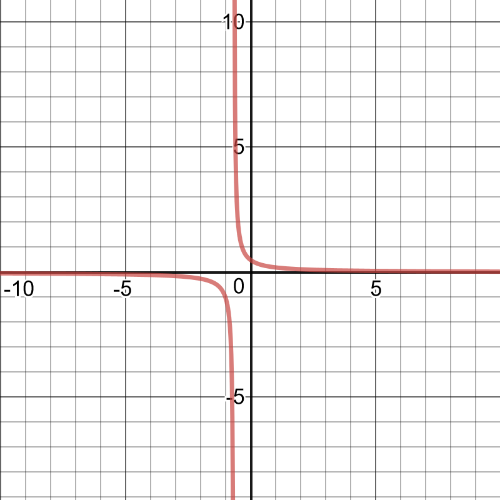
On the following picture there is $textbf{a graph}$ of the function $y=dfrac{1}{3x+2}$:

#### (b)

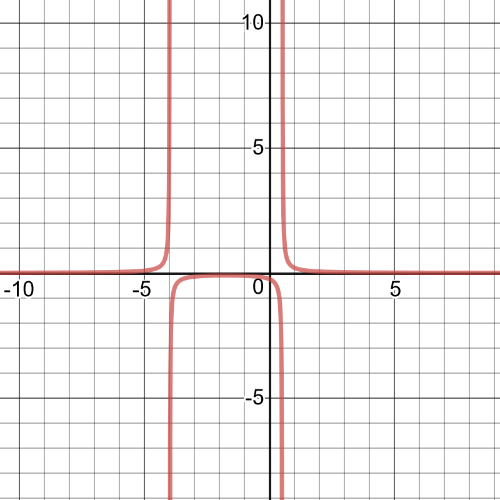
This function is quadriatic function and so $textbf{the domain}$ will be set $D=Bbb{R}$.The coefficient of the first term is positive and so the graph wil be pointed up.The function factors to $f(x)=(2x-1)(x+4)$, so, the $textbf{$x$-intercepts}$ are $x=0.5$ and $x=-4$.The graph will be $textbf{positive}$ on $(-infty,-4)$ and $(0.5,infty)$.The graph will be $textbf{negative}$ on $(-4,0.5)$.$textbf{The range}$ of the function will be set $R=left{yinBbb{R}|y>-10.125 right}$.The graph will be $textbf{decreasing}$ on $(-infty,-10.125)$ and $textbf{increasing}$ on $(-10.125,infty)$.On the following picture there is $textbf{a graph}$ of the function $y=dfrac{1}{2x^2+7x-4}$.

#### (c)

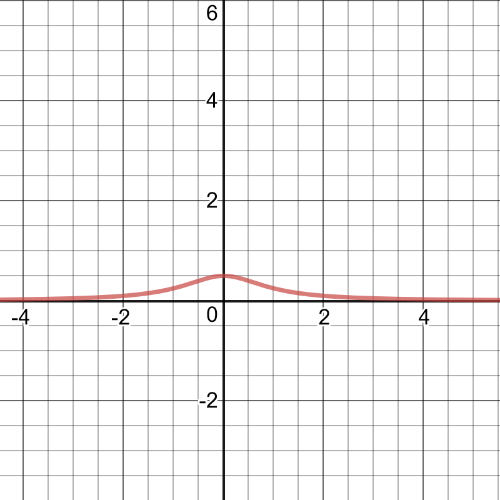
The function s quadriatic function, so, $textbf{the domain}$ will be set $D=Bbb{R}$.Because there are no real solutions to $0=2x^2+2$, the graph will have $textbf{no $x$-intercepts}$.The $textbf{$y$-intercept}$ is $y=2cdot0^2+2=2$.This means that $textbf{the range}$ is set $R=left{yinBbb{R}|y>2 right}$.This function is $textbf{increasing}$ on $(-infty,0)$ and $textbf{decreasing}$ on $(0,infty)$.Because the function has no $x$-intercepts and because the graph is facing up, the function will always be $textbf{positive}$.On the following picture there is a graph of a function $y=dfrac{1}{2x^2+2}$.

Examine each graph. Glean any information from these graphs that might help you to graph their function’s reciprocals.

#### (a)

The function is linear. The domain and range are all real numbers. It is always decreasing.
The $x$-intercept is $x=2.5$. The $y$-intercept is $y=5$.
The function is positive on$(-infty, 2.5)$ and negative on $(2.5, infty)$.
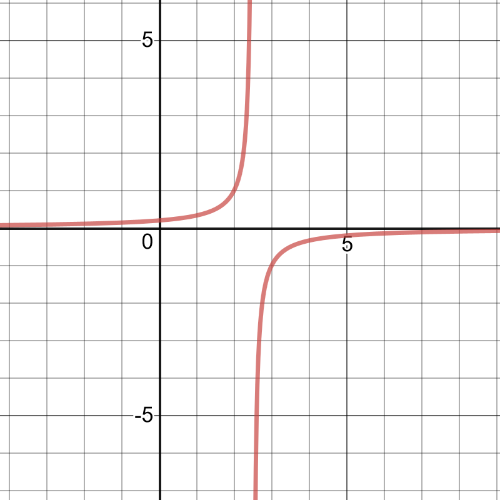
The graph of the reciprocal function would be:

#### (b)

The function is a quadratic equation, which means that the domain of the function is $left{ x in Bbb{R} right}$.The $x$-intercepts of the function are $x=-3$ and $x=4$. The function is
$f(x)=(x+3)(x-4)=x^2-x-12$.The $y$-intercept of the function is $(0, -12).$The vertex can be found by finding the half-way point between the $x$-intercepts.
$dfrac{-3+4}{2}= 0.5$

$f(0.5)=((0.5)+3)((0.5)-4)= (3.5)(-3.5)= -12.25$

The vertex is $(0.5, -12.25)$. This means that the range of the function is $left{y in Bbb{R}|y > -12.25 right}$.The function is decreasing on $(-infty, -12.25)$ and increasing on $(-12.25, infty)$. Use this information to graph the reciprocinal of the function.

#### (a)

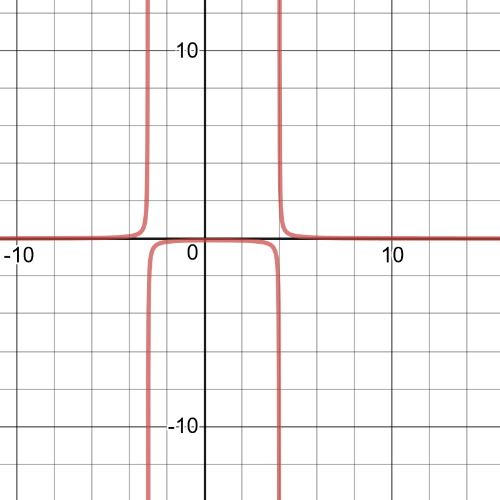
To find $textbf{the vertical asymptote}$ find the zeros of the expression in the denominator:

$0=x+17 Rightarrow x=-17$

Because the numerator of the rational function is a constant, $textbf{the horizontal asymptote}$ would be $y=0$.
#### (b)

To find $textbf{the vertical asymptote}$ find the zeros of the expression in the denominator:

$0=5x+3 Rightarrow 5x=-3 Rightarrow x=-dfrac{3}{5}$

Divide the leading coefficient of the numerator and denominator to find the equation of $textbf{horizontal asymptote}$:

$y=dfrac{2x}{5x}=dfrac{2}{5}$

#### (c)

To find $textbf{the vertical asymptote}$ find the zeros of the expression in the denominator:

$0=-4x^2-42x+22 Rightarrow 0=(x+11)(x-0.5)$

So, we can conclude that euqtions of vertical asymptotes are $x=-11$ and $x=0.5$.

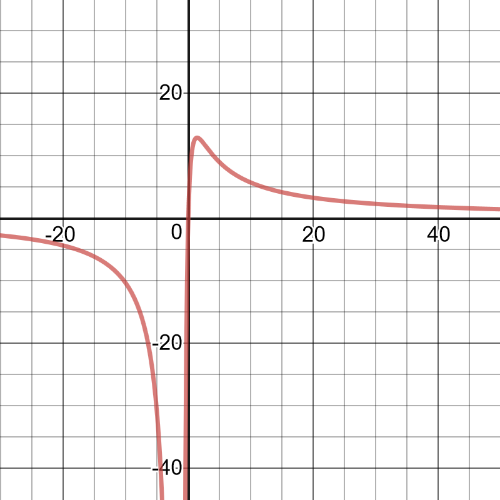
Notice that $(x+11)$ is a factor in both the denominator and the numerator, this means that there is $textbf{a hole}$ at $x=-11$.Because the degree of the expression in the denominator is $2$ and the degree of the expression in the numerator is $1$, $textbf{the horizontal asymptote}$ will bw $y=0$.

#### (d)

To find $textbf{the vertical asymptote}$ find the zeros of the expression in the denominator:

$0=x-1 Rightarrow x=1$

So, the equation of vertical asymptote is $x=-1$.

Because the degree of the expression in the denominator is $2$ and the degree of the expression in the denominator is $1$, there will be an $textbf{oblique asymptote}$.Divide the numerator by the denominator, the non-remainder part is the equation of the oblique asymptote:

$y=3x+3$.

The function that models the population of the locustus is $f(x)=dfrac{75x}{x^2+3x+2}$.You can graph the function using a graphing calculator and then use the graph to describe the loust population over time.From following graph we can see that $textbf{the locust population increased during the first $1.75$ years, to reach a maximum of $1248000$}$.$textbf{The population gradually decreased until the end of the $50$ years, when the population was $128000$}$.

#### (a)

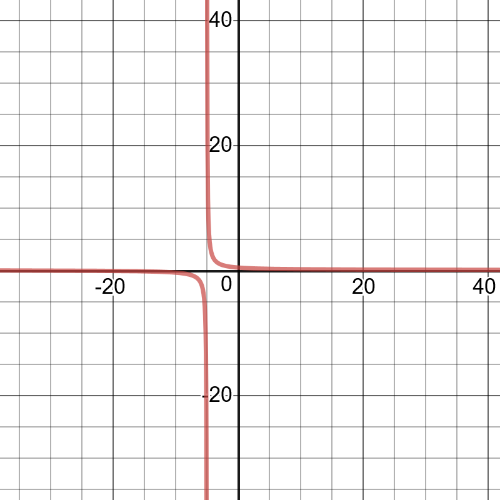
$textbf{This function does not intercept $x$-axis}$.This means that the $textbf{horizontal asymptote}$ is $y=0$.

$y$-intercept: $f(0)=dfrac{2}{0+5}=dfrac{2}{5}$

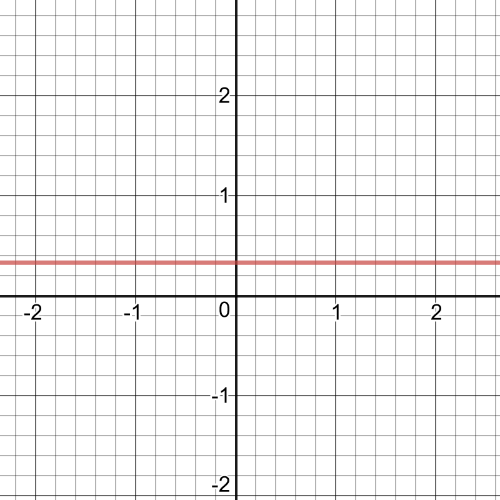
The function has $textbf{a vertical asymptote}$ at $x=-5$.This means $textbf{that domain}$ of the function is set $D=left{xinBbb{R}|xne-5 right}$.The function will be $textbf{negative}$ for $x-5$.On the following picture there is $textbf{a graph}$ of this function.This function is $textbf{decreasing}$ on its domain.

#### (b)

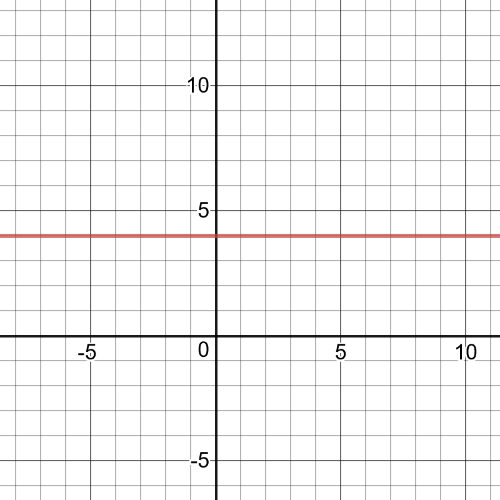
Notice that the function factors to $f(x)=dfrac{4(x-2)}{x-2}=4$.

This means that there will be $textbf{a hole}$ at $x=2$ and the garph opf the function will be the horizontal line $y=4$.The function is $textbf{positive}$ everywhere except $x=2$.$textbf{There is no $x$-intercept}$ and $y$-intercept is $y=4$.The function is $textbf{constant}$.On the following picture there is $textbf{a graph}$ of this function.

#### (c)

Notice that the function factors to $f(x)=dfrac{x-6}{3(x-6)}=dfrac{1}{3}$.

This means that there will be $textbf{a hole}$ at $x=6$ and the garph of the function will be the horizontal line $y=dfrac{1}{3}$.The function is $textbf{positive}$ everywhere except $x=6$.$textbf{There is no $x$-intercept}$ and $y$-intercept is $y=dfrac{1}{3}$.The function is $textbf{constant}$.On the following picture there is $textbf{a graph}$ of this function.

#### (d)

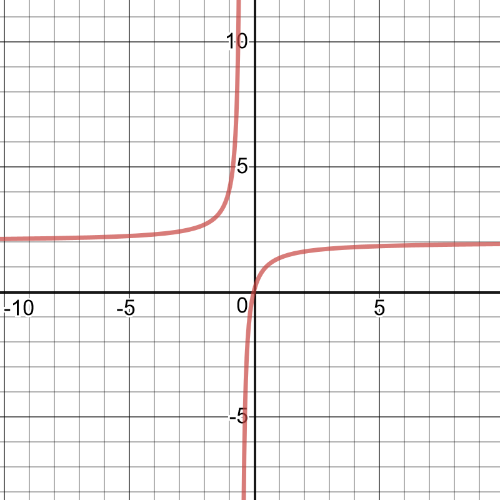
To find $textbf{vertical asymptote}$ of this function, we need to find zero of the expression in the denominator.

$0=2x+1 Rightarrow 2x=-1 Rightarrow x=-dfrac{1}{2}=-0.5$

The function will have a $textbf{vertical asymptote}$ at $x=-0.5$.This means that $textbf{the domain}$ is set $D=left{xinBbb{R}|x-0.5 right}$.

$x$-intercept: $dfrac{4x}{2x+1}=0 Rightarrow 4x=0 Rightarrow x=0$

$y$-intercept: $dfrac{4cdot0}{2cdot0+1}=0$

Divide the first terms of the expressions in the numerator and the denominator to find the equation of the $textbf{horizontal asymptote}$:

$y=dfrac{4x}{2x}=2$

Use the following table to determine when the function is positive and negative. We can see that function is $textbf{positive}$ on $x0$ and $textbf{negative}$ on $-0.5<{x}<0$.

We can see from following graph that this function is $textbf{increasing}$ on $(-infty,-0.5)$ and $(-0.5,infty)$.

Answers may vary. For example, consider the function $f(x)=dfrac{1}{x-6}$.You know that the vertical asymptote would be $x=6$. If you were to find the value of the function very close to $x=6$ say $f(5.99)$ or $f(6.01))$ you would be able to determine the behaviour of the function on either side of the asymptote.

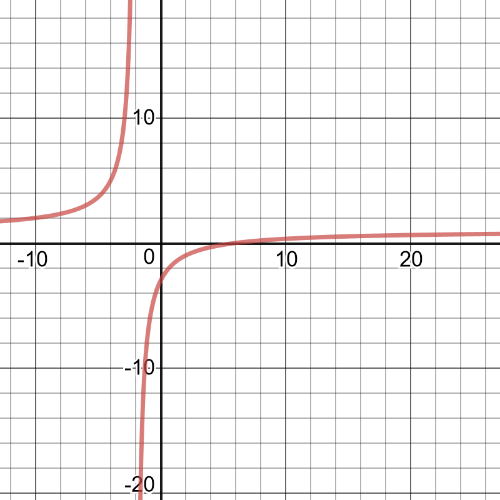
$f(5.99)=dfrac{1}{(5.99)-6}=-100$

$f(6.01)=dfrac{1}{(6.01)-6}=100$

To the left of the vertical asymptote the function moves towards $-infty$.To the right of the asymptote the function moves towards $infty$.

#### (a)

$dfrac{x-6}{x+2}=0 Leftrightarrow x-6=0 Leftrightarrow x=6$

On the following picture there is $textbf{a graph}$ from which we can see solution:

#### (b)

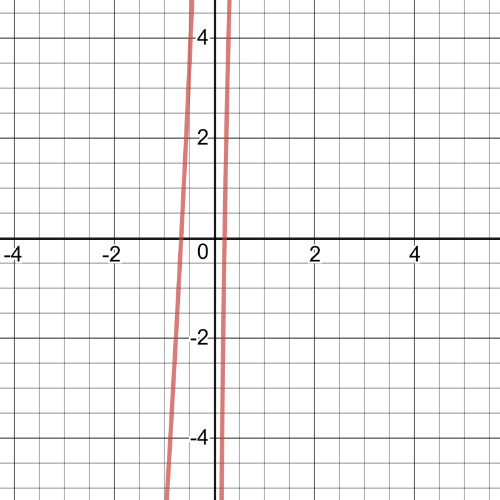
$15x+7=dfrac{2}{x} /cdot{x}$

$x(15x+7)=2$

$15x^2+7x-2=0$

The roots of this function are $x=0.2$ and $x=-dfrac{2}{3}$, which we can see from the following $textbf{graph}$.

#### (c)

$dfrac{2x}{x-12}=dfrac{-2}{x+3} /(x-12)(x+3)$

$2x(x+3)=-2(x-12)$

$2x^2+6x=-2x+24$

$2x^2+8x-24=0$

$2(x+6)(x-2)=0$

We can conclude that $textbf{solutions}$ are $x=-6$ or $x=2$, which we can see from the following $textbf{graph}$.

#### (d)

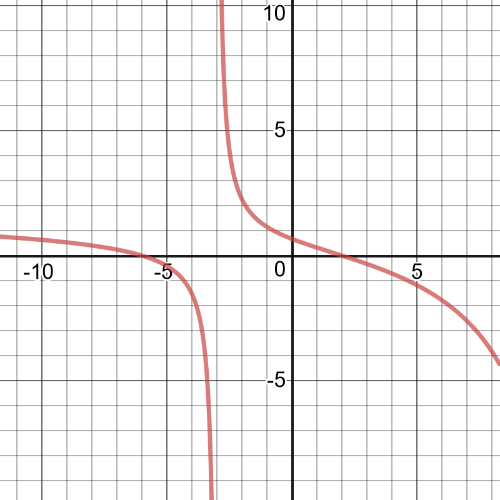
$dfrac{x+3}{-4x}=dfrac{x-1}{-4} /(-4x)$

$x+3=x(x-1)$

$x+3=x^2-x$

$x^2-2x-3=0$

$(x+1)(x-3)=0$

We can conclude that $textbf{solutions}$ are $x=-1$ or $x=3$, which we can see from the following $textbf{graph}$.

(a)$x=6$; (b) $x=0.2$, $x=-dfrac{2}{3}$; (c) $x=-6$, $x=2$; (d) $x=-1$, $x=3$

Janet and Nick’s rate would be $dfrac{1}{m}$ and Rodriguez’s rate would be $dfrac{1}{m-5}$.Working together their rate would be $dfrac{2}{m}+dfrac{1}{m-5}$, which is equal to $dfrac{1}{32.3}$.

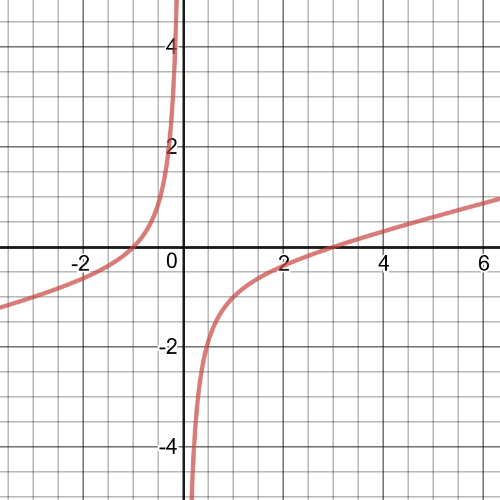
$dfrac{2}{m}+dfrac{1}{m-5}=dfrac{1}{3.23}$

$3.23m(m-5)(dfrac{2}{m}+dfrac{1}{m-5}=dfrac{1}{3.23})$

$3.23(m-5)(2)+3.23m=m(m-5)$

$6.46m-32.3+3.23m=m^2-5m$

$0=m^2-14.69m+32.3$

Use the quadratic formula to determine the roots of this quadratic equation.
$m=12$ and $2.69$

The possible answers are $12$ minutes and $2.69$ minutes. But because Janet’s time has to be grater than $5$ minutes, $textbf{the answer must be $12$ minutes.}$ It takes Janet about $12$ minutes to wash the car.

$12$ minutes

The function that represents the concetration of a toxic chemical is

$c(x)=dfrac{50x}{x^2+3x+6}$.
To determine when the contrecation is $6.16 g/L$ solve the equation
$6.16=dfrac{50x}{x^2+3x+6}$
.

$6.16=dfrac{50x}{x^2+3x+6}$

$6.16(x^2+3x+6)=dfrac{50x}{x^2+3x+6}(x^2+3x+6)$

$6.16x^2+18.48x+36.96=50x$

$6.16x^2-31.52x+36.96=0$

Use the quadratic formula to solve this equation. $x=3.297$ and $1.82$

$$
textbf{The contrecation of the chemical will be $6.16 g/L$ at $1.82$ and $3.297$ days.}
$$

$6.16 g/L$ at $1.82$ and $3.297$ days

#### (a)

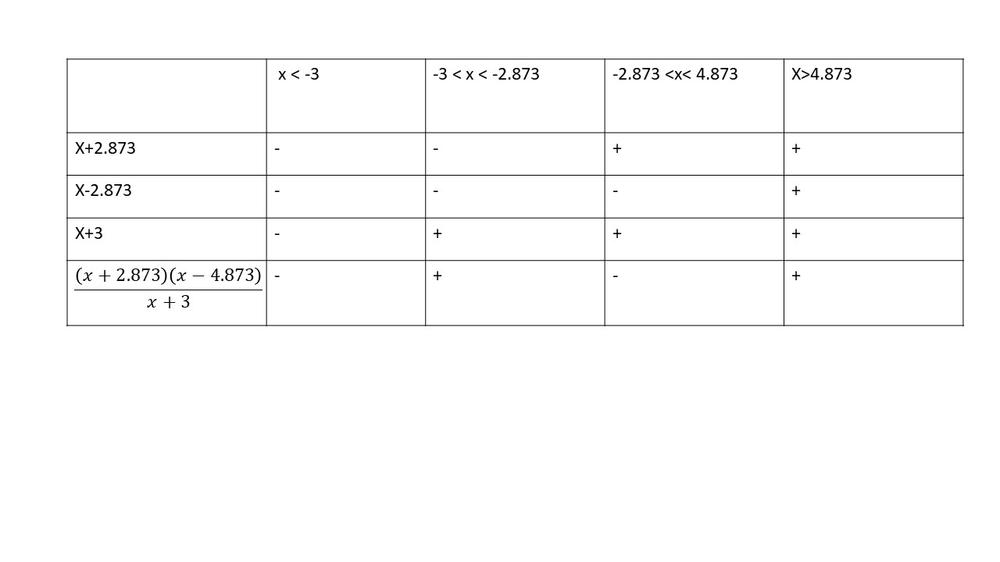
$-x+5<dfrac{1}{x+3}$

$-x+5-dfrac{1}{x+3}<0$

$(dfrac{x+3}{x+3})(-x)+(dfrac{x+3}{x+3})5-dfrac{1}{x+3}<0$

$dfrac{-x^2-3x}{x+3}+dfrac{5x+15}{x+3}-dfrac{1}{x+3}<0$

$dfrac{-x^2+2x+14}{x+3}<0$

$dfrac{(x+2.873)(x-4.873)}{x+3}<0$

$textbf{The inequality is true on $x<-3$ and $-2.873 < x < 4.873$.}$

#### (b)

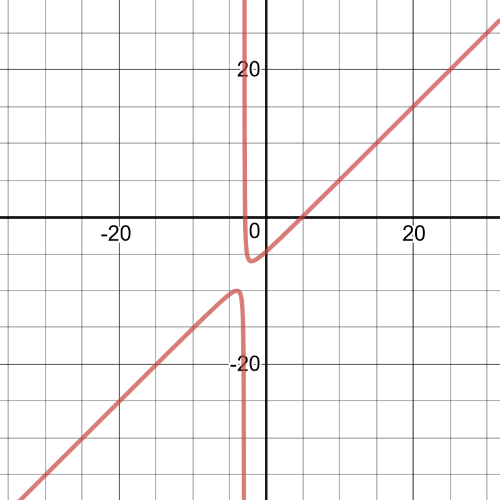
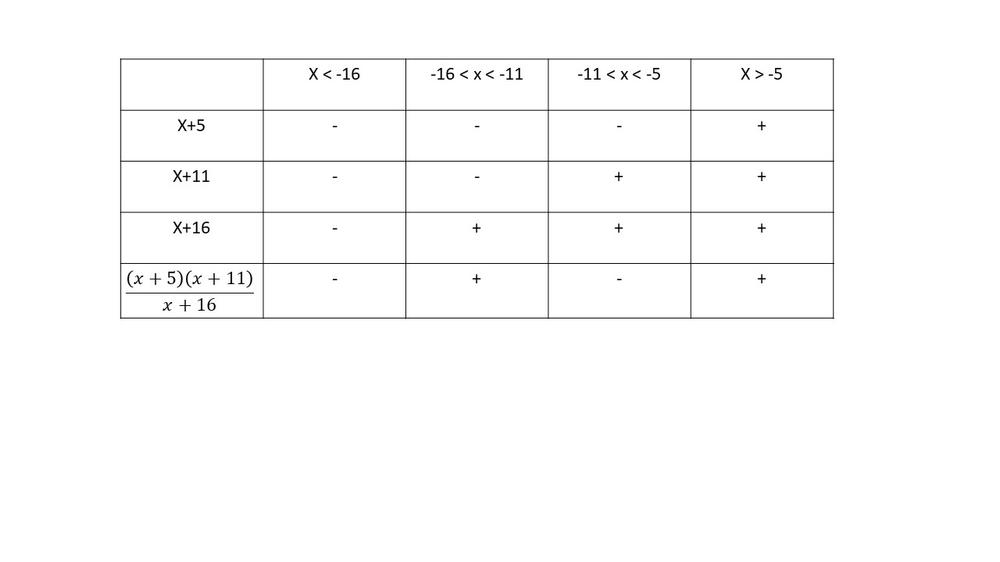
$dfrac{55}{x+16} >-x$

$dfrac{55}{x+16}+x>0$

$dfrac{55}{x+16}+(dfrac{x+16}{x+16})x>0$

$dfrac{x^2+16x+55}{x+16}>0$

$dfrac{(x+5)(x+11)}{x+16}>0$

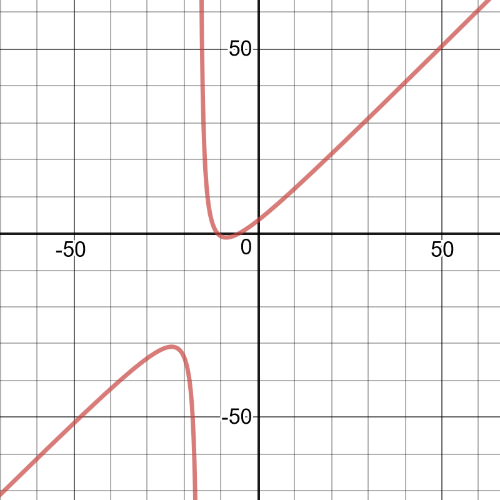
$textbf{This ineqiality is true on $-16<{x}-5$}$.

#### (c)

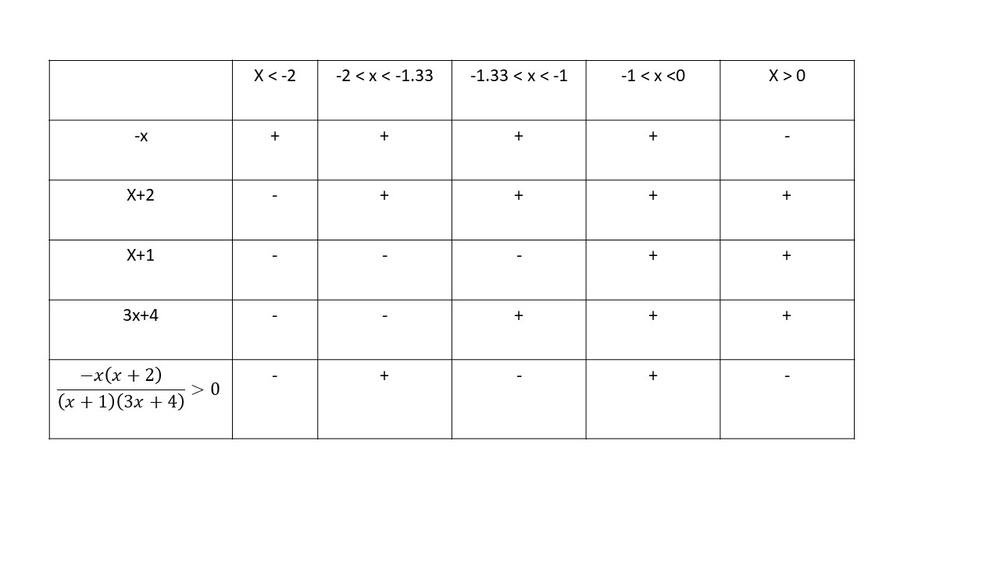
$dfrac{2}{3x+4}>dfrac{x}{x+1}$

$dfrac{2x}{3x+4}-dfrac{x}{x+1}>0$

$(dfrac{x+1}{x+1})dfrac{2x}{3x+4}-dfrac{x}{x+1}dfrac{3x+4}{3x+4}>0$

$dfrac{2x^2+2x}{(x+1)(3x+4)}-dfrac{3x^2+4x}{(x+1)(3x+4)}>0$

$dfrac{-x^2-2x}{(x+1)(3x+4)}>0$

$dfrac{-x(x+2)}{(x+1)(3x+4)}>0$

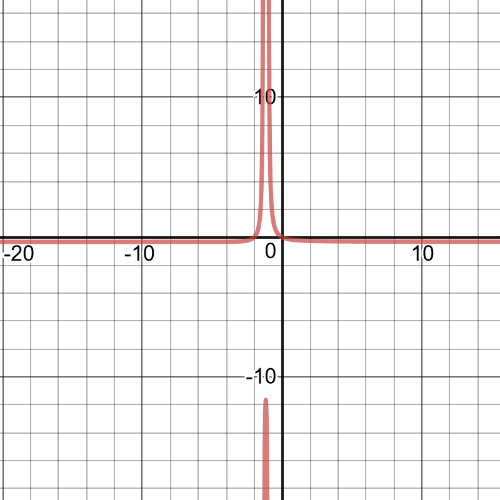
$textbf{The inequality is true on}$ $-2 < x < -1.33$ and $-1 < x <0$.

#### (d)

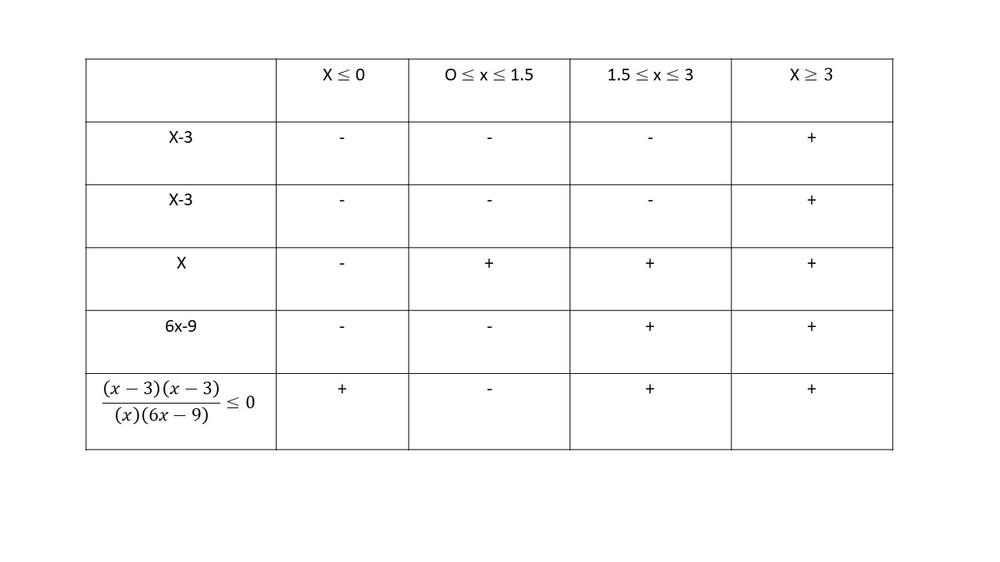
$dfrac{x}{6x-9}leq dfrac{1}{x}$

$dfrac{x}{6x-9}-dfrac{1}{x}leq 0$

$(dfrac{x}{x})dfrac{x}{6x-9}-dfrac{1}{x}(dfrac{6x-9}{6x-9})leq 0$

$dfrac{x^2}{(x)(6x-9)}+dfrac{-6x+9}{(x)(6x-9)}leq 0$

$dfrac{x^2-6x+9}{(x)(6x-9)}leq 0$

$dfrac{(x-3)(x-3)}{(x)(6x-9)}leq 0$

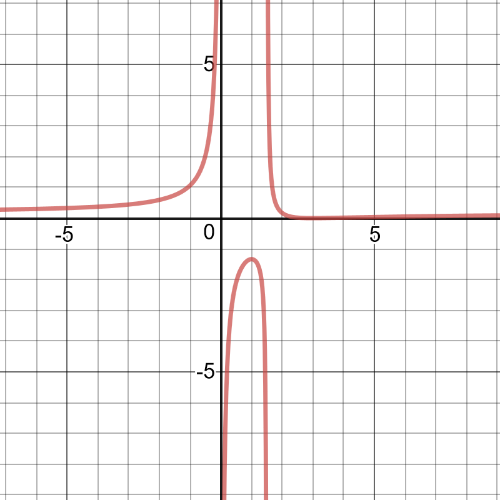
$$
textbf{The inequality is true on $0 < x < 1.5$.}
$$

(a) $x<-3$ and $-2.873 < x < 4.873$

(b)$-16<{x}-5$

(c) $-2 < x < -1.33$ and $-1 < x <0$

(d) $0 < x < 1.5$

The function that models the biologist’s prediction of the population of the tadpoles in the pond is

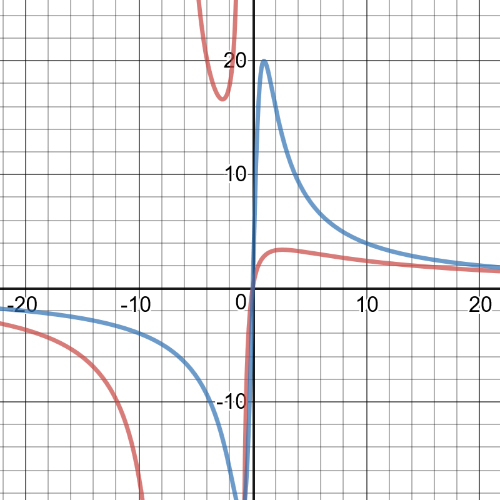
$f(t)=dfrac{40t}{t^2+1}$. The actual population is modelled by

$g(t)=dfrac{45t}{t^2+8t+7}$. Graph $dfrac{45t}{t^2+8t+7}$ and $dfrac{40t}{t^2+1}$ to determine where $g(t)>f(t)$.

$$
textbf{$g(t)$ appears to be greater than $f(t)$ on $-6.7<x<-1.01$ and $-0.73<x<0$.}
$$

$f(t)$ on $-6.7<x<-1.01$ and $-0.73<x<0$

The slope of the line tangent to the graph for the given point is equal to the instantaneous rate of change at that point. Use the difference quotient to determine the instantaneous rate of change.The point where a vertical asymptote occurs is the point where no tangent line could be drawn.

$dfrac{x+3}{x-3}, x=4$

$f(4)= dfrac{4+3}{4-3}=7$

$f(4.01)=dfrac{4.01+3}{4.01-3}=6.94$

$textbf{Difference Quotient}$=$dfrac{6.94-7}{0.01}=dfrac{-0.06}{0.01}=-6$

$$
textbf{The vertical asymptote occurs at $x=3$}
$$

#### (b)

$f(x)=dfrac{2x-1}{x^2+3x+2}, x=1$

$f(1)=dfrac{2(1)-1}{(1)^2+3(1)+2}=0.167$

$f(1.01)=dfrac{2(1.01)-1}{(1.01)^2+3(1.01)+2}=0.169$

$textbf{Difference Quotient}$=$dfrac{0.169-0.167}{0.01}=dfrac{0.002}{0.01}=0.2$

$$
textbf{The vertical asymptotes occur at $x=-2$ and $x=-1$.}
$$

(a) $x=3$

(b) $x=-2$ and $x=-1$

#### (a)

To find the average rate of change during the first two hours of the drug’s ingestion, find $c(2)$ and $c(0)$

$c(2)=dfrac{5(2)}{(2)^2+7}=dfrac{10}{11}=0.91$

$c(0)=dfrac{5(0)}{(0)^2+7}=0$

Average Rate of Change:

$dfrac{0.91-0}{2-0}=0.455 mg/L/h$

#### (b)

Use the difference quotient to help you determine the drug’s instantaneous rate of change at $t=3$.

$c(3)=dfrac{5(3)}{(3)^2+7}=0.9375$

$c(3.01)=dfrac{5(3.01)}{(3.01)^2+7}=dfrac{15.05}{16.0601}=0.9371$

Difference Quotient = $dfrac{0.9371-0.9375}{0.01}=dfrac{-0.004}{0.01}=-0.04 mg/L/h$

#### (c)

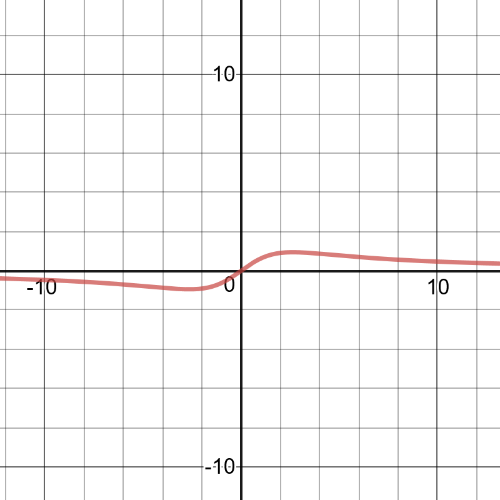
Graph the function $c(t)=dfrac{5t}{t^2+7}$.

$textbf{The concetration of the drug in the blood stream appears to be increasing most rapidly during the first hour and a half: the graph is steep and increasing during this time}$.

(a) $0.455 mg/L/h$

(b) $-0.04 mg/L/h$

(c) see solution

The slope of the tangent line is going to be $dfrac{4-10}{8-5}= -2$. This means that the equation of the line would be $y=-2x+20$. You are looking for the point of intersection between the two functions, and so you need to solve $-2x+20=dfrac{2x}{x-4}$.

$-2x+20=dfrac{2x}{x-4}$

$(-2x+20)(x-4)=2x$

$-2x^2+8x+20x-80=2x$

$-2x^2+26x-80=0$

$x^2-13x+40=0$

$(x-5)(x-8)=0$

The two points of intersection would be $x=5$ and $x=8$. The point with the line parallel to the secant line would lie half-way in between these two points, $x=6.5$.

$x=5$ and $x=8$

$x=6.5$

#### (a)

As the $x$-coordinate approaches the vertical asymptote of a rational function, the line tangent to the graph will get closer and closer to being a vertical line. This means that the slope of the line tangent to the graph will get larger and larger, approaching positive or negative infinity depending on the function, as $x$ get closer to the vertical asymptote.

#### (b)

As the $x$-coordinate grows larger and larger in either direction, the line tangent to the graph will get closer and closer to being a horizontal line. This means that the slope of the line tangent to the graph will always approach zero as $x$ gets larger and larger.