
All Solutions
Page 303: Check Your Understanding
Use the graph to determine $f(2)$ and $f(7)$.
$f(2)=4$
$f(3)=1.5$
$y=dfrac{1.5-4}{7-2}=-0.5$
#### (b)
$textbf{The slope of the tangent line is}$ $-3$, we can see that from following gaph:
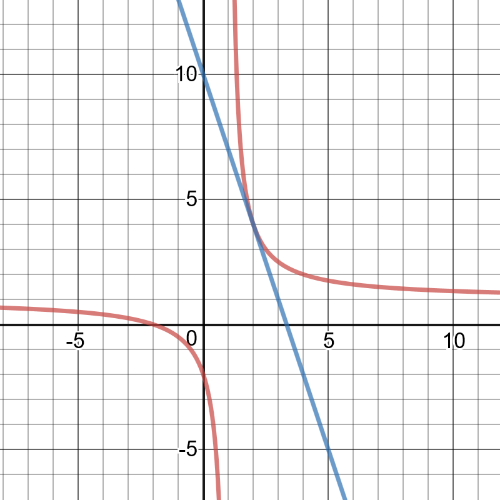
$dfrac{f(a+h)-f(a)}{h}=dfrac{f(2)-f(2.01)}{0.01}=dfrac{3.97-4}{0.01}=-3$
$textbf{So, the answers at $1.$ task and here match}$.
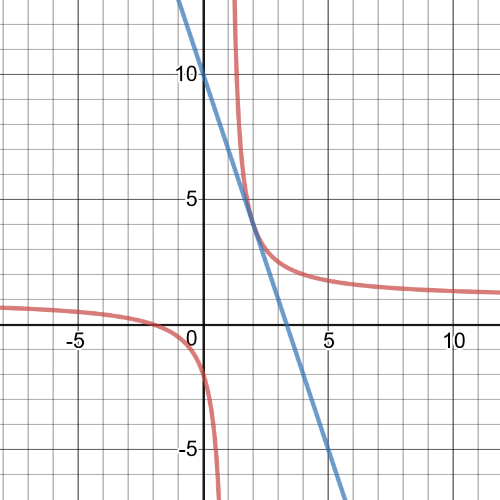
$f(x)=dfrac{f(a+h)-f(a)}{h}$, we can use $h=0.01$.
$f(2.01)=dfrac{2.01}{2.01-4}=-1.01$
$textbf{Difference quotient}$ = $dfrac{-1.01-(-1)}{0.01}=-1$
#### (a)
$y=dfrac{1}{25-x}, x=13$
$f(13)=dfrac{1}{25-13}=dfrac{1}{12}$
$f(13.01)=dfrac{1}{25-13.01}=dfrac{1}{11.999}$
$textbf{Difference Quotient}$ = $dfrac{dfrac{1}{11.99}-dfrac{1}{12}}{0.001}=0.01$
#### (b)
$y=dfrac{17x+3}{x^2+6}, x=-5$
$f(-5)=dfrac{17(-5)+3}{(-5)^2+6}=-2.645$
$f(-4.99)=dfrac{17(-4.99)+3}{(-4.99)^2+6}=-2.648$
$textbf{Difference Quotient}$ = $dfrac{-2.648-(-2.645)}{0.01}=-dfrac{0.003}{0.01}=-0.3$
#### (c)
$y=dfrac{x+3}{x-2}, x=4$
$f(4)=dfrac{4+3}{4-2}=3.5$
$f(4.01)=dfrac{4.01+3}{4.01-2}=3.487$
$textbf{Difference Quotient}$ = $dfrac{3.487-3.5}{0.01}=-dfrac{0.013}{0.01}=-1.3$
$y=dfrac{-3x^2+5x+6}{x+6}, x=-3$
$f(-3)=dfrac{-3(-3)^2+5(-3)+6}{-3+6}=6$
$f(-3.01)=dfrac{-3(-3.01)^2+5(-3.01)+6}{-3.01+6}=6.06$
$textbf{Difference Quotient}$ = $dfrac{6.06-6}{0.01}=-dfrac{0.06}{0.01}=6$
#### (a)
$f(x)=dfrac{-5x}{2x+3}, x=2$
$f(2)=dfrac{-5(2)}{2(2)+3} = dfrac{-10}{7}= -1.429$
$f(2.01)=dfrac{-5(2.01)}{2(2.01)+3}= -1.432$
$textbf{Difference Quotient}$ = $dfrac{1.432-(-1.429)}{0.01}=286.1$
$textbf{The vertical asymptote would occur at $x= -1.5$}$.
#### (b)
$f(x)=dfrac{x-6}{x+5}, x= -7$
$f(-7) = dfrac{(-7)-6}{(-7)+5}=dfrac{-13}{-2}= 6.5$
$f(-7.01)=dfrac{(-7.01)-6}{(-7.01)+5}= dfrac{-13.01}{-2.01}= 6.4726$
$textbf{Difference Quotient}$ = $dfrac{6.4726-6.5}{0.01}= -2.74$
$textbf{The vertical asymptote would occur at}$ $x = -5$
$f(x)=dfrac{2x^2-6x}{3x+5}, x= -2$
$f(-2)=dfrac{2(-2)^2-6(-2.01)}{3(-2)+5}= -20$
$f(-2.01)=dfrac{2(-2.01)^2-6(-2.01)}{3(-2.01)+5}= -19.5535$
$textbf{Difference Quotient}$= $dfrac{-19.5535-(-20)}{0.01}= 44.65$
$textbf{The vertical asymptote would occur at}$ $x= -dfrac{5}{3}$
#### (d)
$f(x)=dfrac{5}{x-6}, x= 4$
$f(4)=dfrac{5}{(4)-6}=-2.5$
$f(4.01)=dfrac{5}{(4.01)-6}= -2.5126$
$textbf{Difference Quotient}$ = $dfrac{-2.5126-(-2.5)}{0.01}= -1.26$
$textbf{The vertical asymptotet occurs at $x=6$}$.
(b) $x = -5$
(c) $x= -dfrac{5}{3}$
(d) $x=6$
#### (a)
There are $60$ minutes in $1$ hour, so, find $c(60)$:
$c(60)=dfrac{27cdot60}{10000+3cdotcdot60}=0.1591$
$c(60.01)=dfrac{27cdot60.01}{10000+3cdot60.01}=0.1592$
$textbf{Difference Quotient}$ = $dfrac{0.1592-0.1591}{0.01}=0.01$.
#### (b)
There are 10080 minutes in one week, so, determine c(10080):
$c(10080)=dfrac{27cdot10080}{10000+3cdotcdot10080}=6.76$
$c(10080.01)=dfrac{27cdot10080.01}{10000+3cdot10080.01}=6.7634$
$textbf{Difference Quotient}$ = $dfrac{6.7634-6.76}{0.01}=0.34$.
The demand function is $f(x)=dfrac{15x}{2x^2+11x+5}$.This function tells you
the price of the cakes for every $1000$ cakes.The revenue function would be the number of cakes sold, $x$, times the price of cakes for that number of cakes sold $dfrac{15x}{2x^2+11x+5}$.So, $textbf{the revenue function}$ is $p(x)=dfrac{15x}{2x^2+11x+5}$.
#### (b)
Use the difference quotient to determine the marginal revenue for $x=0.75$ and $x=2$.
$f(x)=dfrac{15x}{2x^2+11x+5}$
$f(0.75)=dfrac{15cdot0.75}{2(0.75)^2+11cdot0.75+5}=0.7826$
$f(0.751)=dfrac{15cdot0.751}{2(0.751)^2+11cdot0.751+5}=0.7829$
$textbf{Difference Quotient}$ = $dfrac{0.7829-0.7826}{0.001}=0.3$
$textbf{The marginal revenue at $x=0.75$ is $0.3$}$
Now, find the marginal revenue for $x=2$:
$f(2)=dfrac{15cdot2}{2cdot2^2+11cdot2+5}=0.8571$
$f(2.01)=dfrac{15cdot2.01}{2cdot2.01^2+11cdot2.01+5}=0.8568$
$textbf{Difference Quotient}$ = $dfrac{0.8568-0.8571}{0.01}=-0.03$
$textbf{The marginal revenue at $x=2$ is $-0.03$}$
(b) The marginal revenue at $x=0.75$ is $0.3$, the marginal revenue at $x=2$ is $-0.03$
Since $x$ is measured in thousands, find $C(3)$.
The function is $C(x)=dfrac{x^2-4x+20}{x}$
$C(3)=dfrac{3^2+4cdot3+4cdot3+20}{3}=5.67$
$$
textbf{The average cost per T-shirt is $5.76$$ .}
$$
#### (b)
Determine $C(3.01)$ and use this value in the difference quotient to help you estimate the average rate of change of the average price of a T-shirt when the factory is producing $3000$ of them.
$C(3.01)=dfrac{3.01^2+4cdot3.01+4cdot3+20}{3.01}=5.65$
$textbf{Difference Quotient}$ = $dfrac{5.65-5.67}{0.01}=-2$
#### (a)
$N(6)=dfrac{100(6)^3}{100+(6)^3}=dfrac{21600}{316}=68.35$
$N(6.01)=dfrac{100(6.01)^3}{100+(6.01)^3}=dfrac{21708.18}{317.08}=68.46$
$textbf{Difference Quotient}$=$dfrac{68.46-68.35}{0.01}=-11$
#### (b)
$N(12)=dfrac{100(12)^3}{100+(12)^3}=dfrac{172800}{1828}=94.53$
$N(12.01)=dfrac{100(12.01)^3}{100+(12.01)^3}=dfrac{173232.36}{1832.32}=94.54$
$textbf{Difference Quotient}$=$dfrac{94.54-94.53}{0.01}=1$
#### (c)
The number of houses that were built increases slowly at first, but rises rapidly between the third and sixth months. During the last six months, the rate at which the houses were built decreases.On the following picture there is a $textbf{graph}$ of given function:
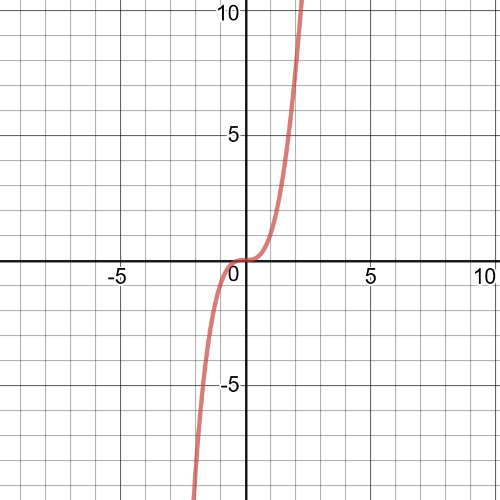
(b)$1$
(c) see solution
$f(15)=dfrac{15-2}{15-5}=dfrac{13}{10}=1.3$
$f(14)=dfrac{14-2}{14-5}=dfrac{12}{9}=1.33$
$dfrac{1.3-1.33}{15-14}= -0.03$
The slope over the interval $14leq x leq15$ is $m=-0.03$,which is approximately $0$. Now find the instantaneous rate of change at $14.5$.
$f(14.5)=dfrac{14.5-2}{14.5-5}=dfrac{12.5}{9.5}=1.316$
$f(14.51)=dfrac{14.51-2}{14.51-5}=dfrac{12.51}{9.51}=1.315$
$dfrac{1.315-1.316}{14.51-14.5}= -0.1$
The instantaneous rate of change at the point $14.5$ is $-0.01$, which is approximately $0$. The rate of change over the interval and at the specific point is about $0$.
$14.5$ is $-0.01$
I would find $s(0)$ and $s(6)$ and would then solve $dfrac{s(6)-s(0)}{6-0}$.
#### (b)
The average rate of change over this interval gives the object’s speed.
#### (c)
To find the instantaneous rate of change at a specific point, you could find the slope of the line that is tangent to the function $s(t)$ at the specific point. $textbf{You could also find the average rate of change on either side of the point for smaller and smaller intervals until it stabilizes to a constant.}$ It is generaly eaiser to find the instantaneous rate using a graph, but the second method is more accurate.
#### (d)
The instantaneous rate of change for a specific time $t$,is the acceleration of the object at this time.
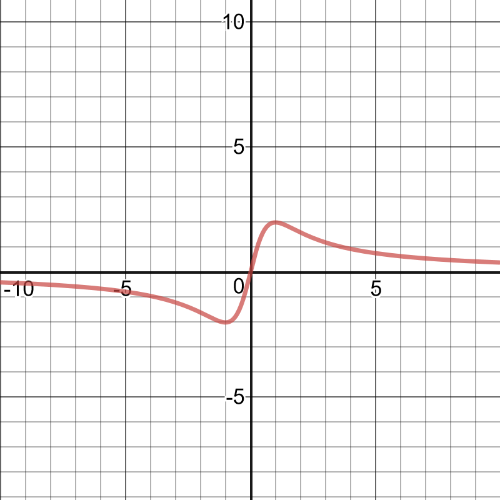
$textbf{The equation of the line tangent to the function at $(-sqrt{3},-sqrt{3})$ is}$ $y=-0.5x-2.598$.
On the following picture is graph of the function and tangent line at the point $(-sqrt{3},-sqrt{3})$
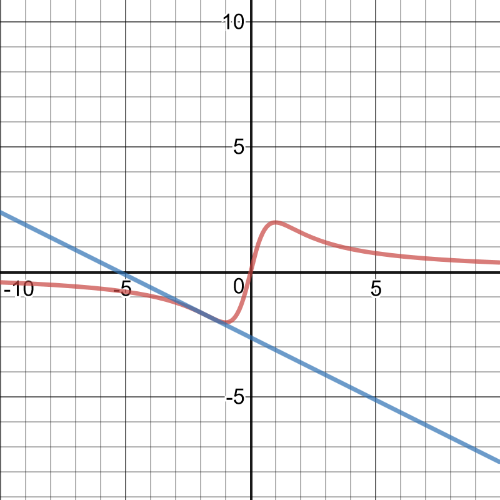
On the following picture there is a graph of the function and tangent line.
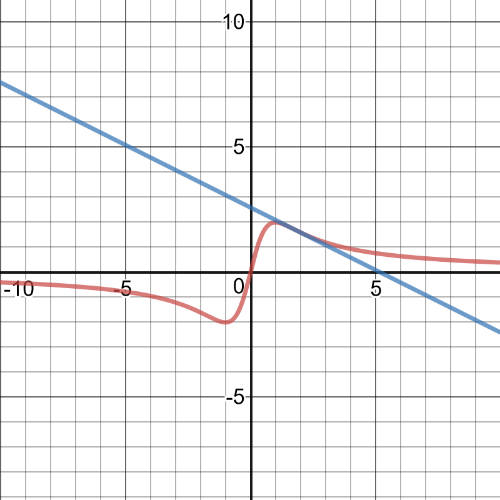
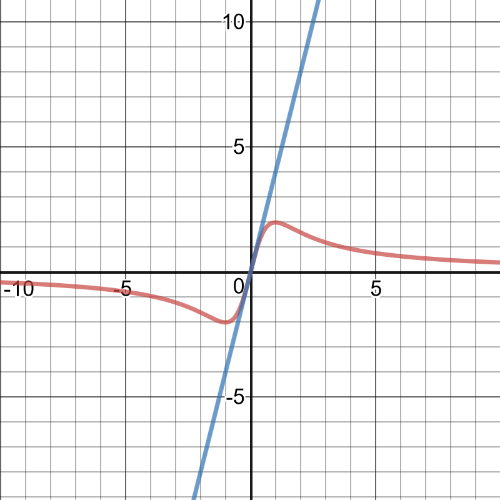
On the following picture there is a graph of the function and tangent line at point $(0,0)$.
$(sqrt{3},sqrt{3})$ – $y=-0.5x+2.598$;
$(0,0)$ – $y=4x$.

