This relation $textbf{is a function}$ because each element in the domain is mapped to exactly one element from the range.

The following sets represent $textbf{the domain and the range}$ of this function:

$D=left{0,3,15,27 right}$

$R=left{2,3,4 right}$

#### (b)

This relation $textbf{is a function}$, because each element in the domain is mapped to exactly one element from the range.We can see that by creating table of values.

The following sets represent $textbf{the domain and the range}$ of this function:

$D=Bbb{R}$

$R=Bbb{R}$

#### (c)

This releation $textbf{is not a function}$ becauseit fails vertical line test, which we mentioned earlier.

The following sets represent $textbf{the domain and the range}$ of this relation:

$D=left[-5,5 right]$

$R=left[-5,5 right]$

This relation $textbf{is not a function}$ because the element 2 is mapped in two elements, in 7 and 6.

The following sets represent $textbf{the domain and the range}$ of this relation:

$D=left{1,2,10 right}$

$R=left{-1,3,6,7 right}$

In this task, we are practically given a table of values ​​from which we see that each element is mapped by a given relation to exactly one element.

On the basis of the above, we conclude that the given mapping $textbf{is a function}$

#### (b)

The $textbf{domain}$ of this function is the following set:

$D=left{0,1,2,3,4,5,6,7,8,9,10 right}$

#### (c)

The $textbf{range}$ of this function is the following set:

$R=left{10,20,25,30,35,,40,45,50 right}$

This relation $textbf{is a function}$, we can see that by forming table of values.

Its $textbf{domain and range}$ are following sets:

$D=Bbb{R}$

$R=Bbb{R}$

#### (b)

This relation $textbf{is not a function}$, because this relation fails vertical line test.

Its $textbf{domain and range}$ are following sets:

$D=left[-3,3 right]$

$R=left[-3,3 right]$

#### (c)

This relation $textbf{is a function}$, we can see that by forming table of values.

Its $textbf{domain and range}$ are following sets:

$D=left{xinBbb{R}|xleq5 right}$

$R=left{yinBbb{R}|ygeq0 right}$

This relation$textbf{ is a function}$, we can also simply see that by forming table of value, and transforming this relation a little into following shape:

$y=x^2-2$

Its $textbf{domain and range}$ are following sets:

$D=Bbb{R}$

$R=left{yinBbb{R}|ygeq2 right}$

$left|-3 right|=left|3 right|$

$left|-4 right|=left|4 right|$

So, the solution of this problem is:

$-left|3 right|leq0leqleft|-3 right|leqleft|-4 right|leqleft|5 right|$

#### (a)

$f(x)=left|x right|+3$

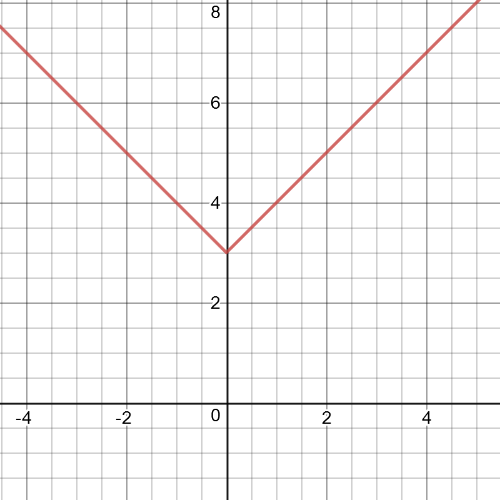
$f(x)=left|x right|-2$

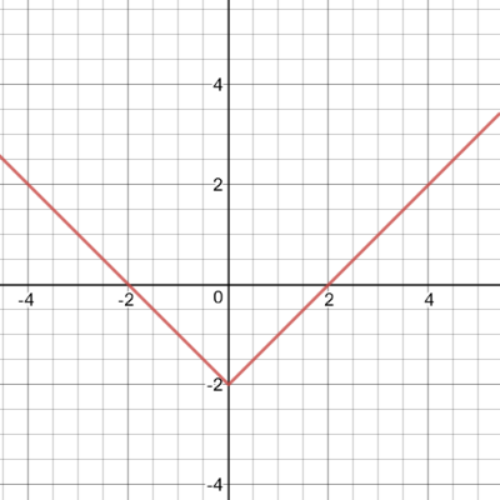
$f(x)=left|-2x right|$

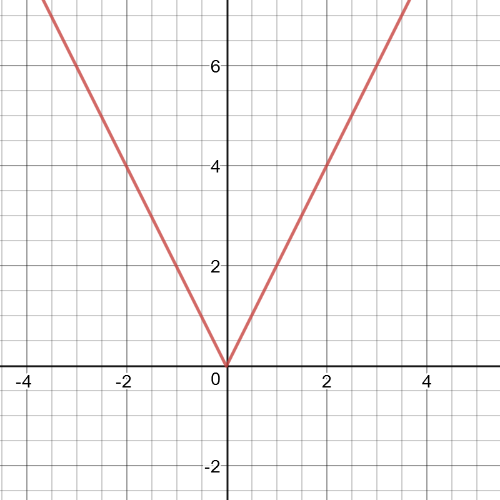
$f(x)=left|0.5x right|$

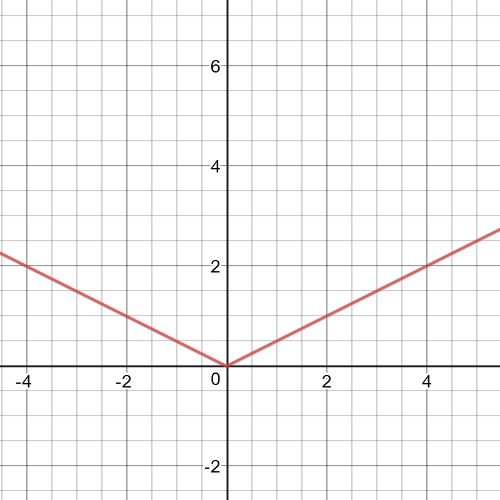
It might be following function:

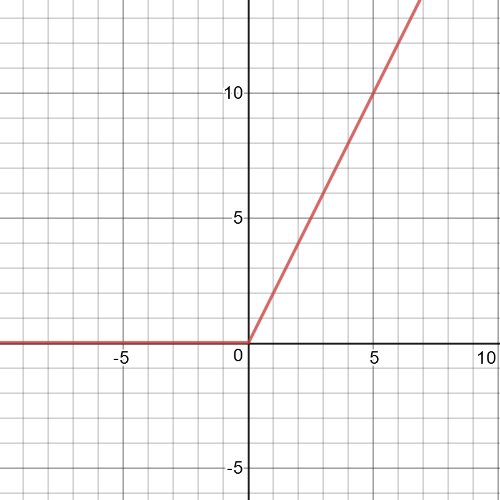
$textbf{$y=left|x right|+x$}$

As proof, we have the graph of this function, where we can see that when $xmapstoinfty$ also $ymapstoinfty$,and that this function is neither even nor odd:

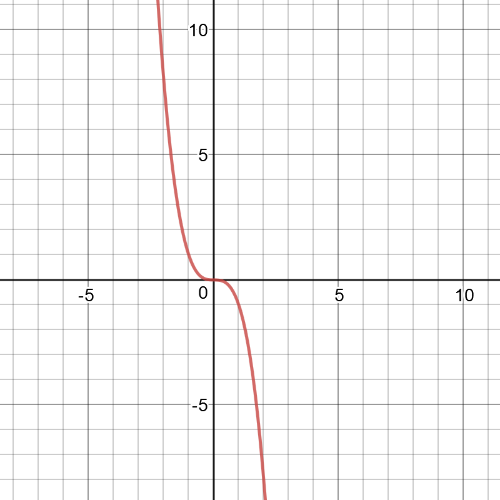
It might be a following function:

$y=-x^3$

Domain of this function is $Bbb{R}$ and it is $textbf{decreasing}$ on $left( -infty,0right)$ and on $left(0,infty right)$, which we can see from the following graph:

It might be function:

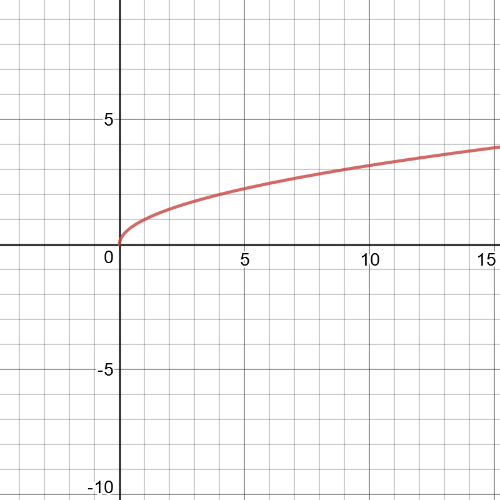
$y=sqrt{x}$

$textbf{Domain}$ of this function is demanded interval $left[0,infty right)$, which we can see from the following graph:

Function $f(x)$ is $textbf{even}$ if $f(-x)=f(x)$

Function $f(x)$ is $textbf{neither}$ if does not satisfy any of previous equation.

#### (a)

$f(-x)=left|-2x right|=left|2x right|=f(x)$

So, we conclude that in this case $f(x)$ is $textbf{even}$ function.

#### (b)

$f(x)=(-x)^2=x^2$

$f(-x)=(-(-x))^2=x^2=f(x)$

So, and here we conclude that $f(x)$ is $textbf{even}$ function.

#### (c)

$f(-x)=-x+4$

We conclude that this function is $textbf{neither}$, because it is not equally to $f(x)$ and to $-f(x)$, where

$$
-f(x)=-(x+4)=-x-4
$$

$f(-x)=4(-x)^2+3(-x)^3-1=4x^2-3x^3-1$

We conclude that this function is $textbf{neither}$, because it is not equally to $f(x)$ or to $-f(x)$, where

$-f(x)=-(4x^2+3x^3-1)=-4x^2-3x^3+1$

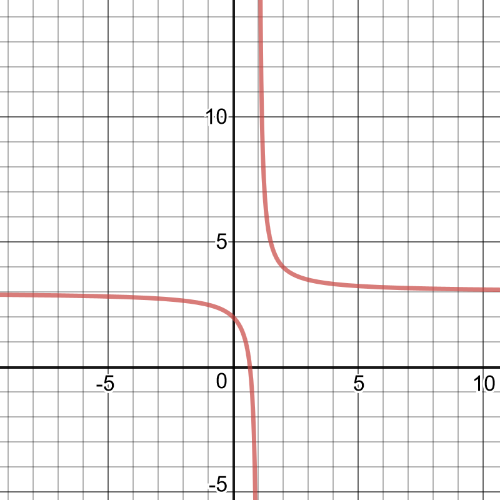
This is $f(x)=dfrac{1}{x}$ $textbf{translated}$ $1$ unit right and $3$ units up, it is $textbf{discontinuous}$.

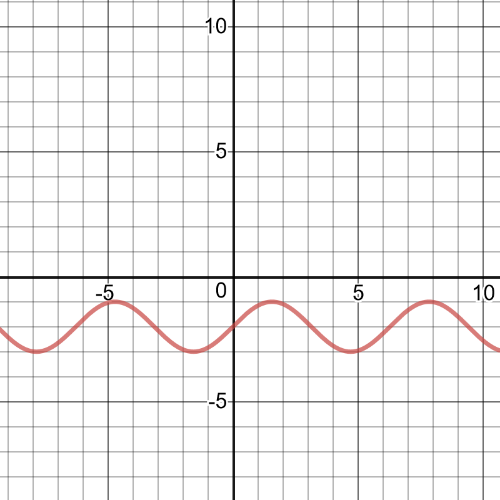
This is $f(x)=sin{x}$ $textbf{translated}$ $2$ units down, it is $textbf{continuous}$.

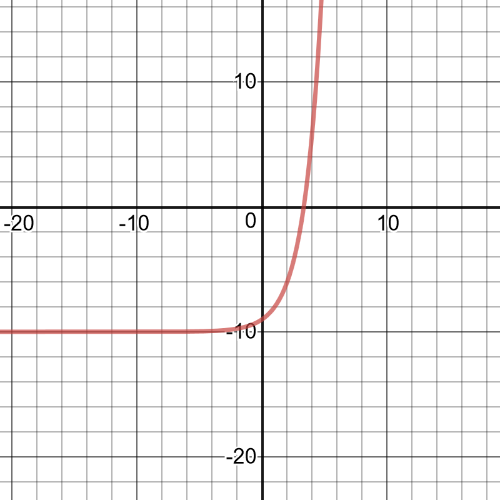
This is $f(x)=2^x$ $textbf{translated}$ $10$ units down, it is $textbf{continuous}$.