#### (a)

$textbf{Equation of reciprocal function}$ is:

$y=dfrac{1}{f(x)}=dfrac{1}{x-3}$

We can conclude that $textbf{vertical asymptote}$ is $x=3$.

#### (b)

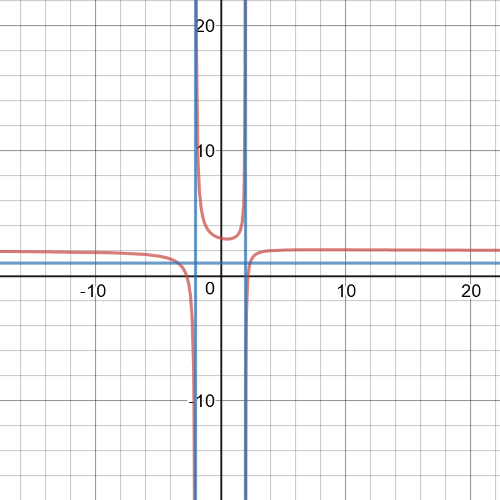
$textbf{Equation of reciprocal function}$ is:

$y=dfrac{1}{f(q)}=dfrac{1}{-4q+6}$

We can conclude that $textbf{vertical asymptote}$ is $q=dfrac{3}{2}$.

#### (c)

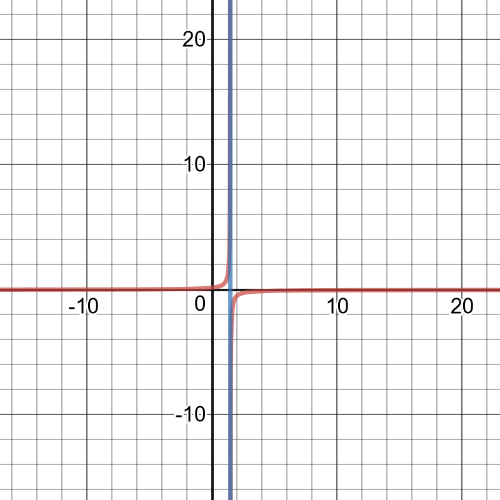
$textbf{Equation of reciprocal function}$ is:

$y=dfrac{1}{f(z)}=dfrac{1}{z^2+4z-5}=dfrac{1}{(z-1)(z+5)}$

We can conclude that $textbf{vertical asymptotes}$ are $z=1$ and $z=-5$.

#### (d)

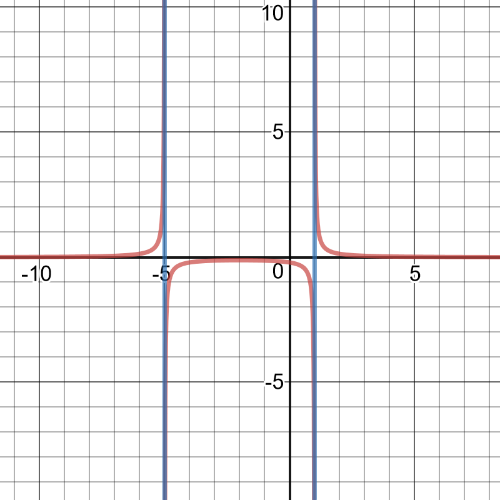
$textbf{Equation of reciprocal function}$ is:

$y=dfrac{1}{f(d)}=dfrac{1}{6d^2+7d-3}=dfrac{1}{(d-dfrac{1}{3})(d+dfrac{3}{2})}$

We can conclude that $textbf{vertical asymptotes}$ are $d=dfrac{1}{3}$ and $d=-dfrac{3}{2}$.

#### (a)

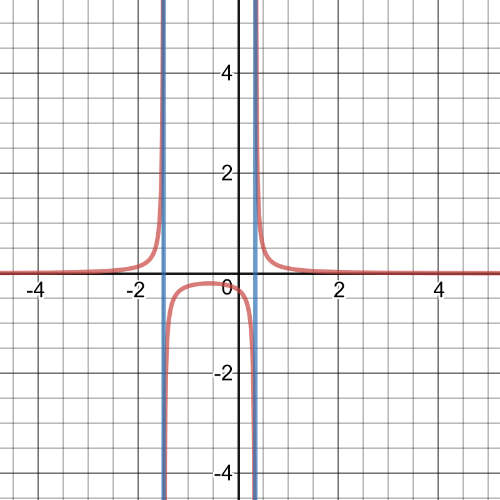
$textbf{The domain and range}$ are the same set, $D=R=Bbb{R}$;

$x$-intercepts is $x=-dfrac{3}{2}$

This function is $textbf{negative}$ on interval $(-infty,-dfrac{3}{2})$ and $textbf{positive}$ on interval $(-dfrac{3}{2},+infty)$;

It is always $textbf{increasing}$.

$textbf{The equation of reciprocal function}$ is $y=dfrac{1}{4x+6}$ and on following graph are original function and reciprocal:

#### (b)

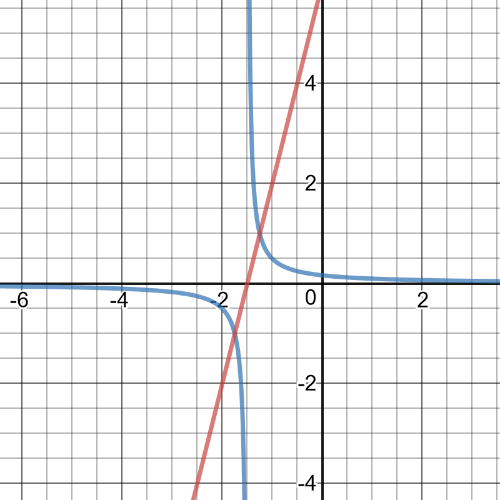
$textbf{The domain}$ of this fumction is set $D=Bbb{R}$ and $textbf{range}$ is set $R=left{yinBbb{R}|y>-4 right}$;

$x$-intercepts are $x=2$ and $x=-2$

This function is $textbf{negative}$ on interval $(-2,2)$ and $textbf{positive}$ on intervals $(-infty,-2)$ and $(2,+infty)$;

It is $textbf{increasing}$ on $(-infty,0)$ and $textbf{decreasing}$ on $(0,+infty)$.

$textbf{The equation of reciprocal function}$ is $y=dfrac{1}{x^2-4}$ and on following graph are original function and reciprocal:

#### (c)

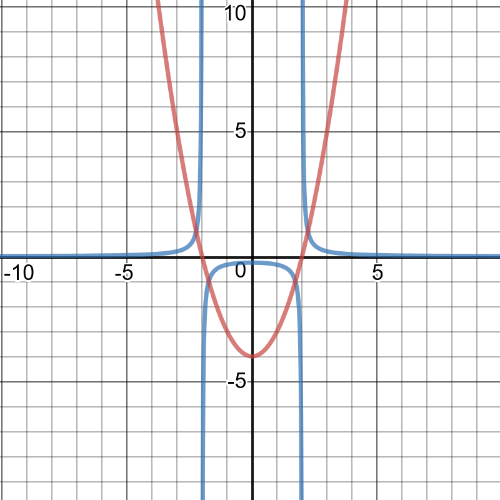
$textbf{The domain}$ of this fumction is set $D=Bbb{R}$ and $textbf{range}$ is set $R=left{yinBbb{R}|y>6 right}$;

This function has no $x$-intercepts

This function is always $textbf{positive}$;

It is $textbf{decreasing}$ on $(-infty,0)$ and $textbf{inreasing}$ on $(0,+infty)$.

$textbf{The equation of reciprocal function}$ is $y=dfrac{1}{x^2+6}$ and on following graph are original function and reciprocal:

#### (d)

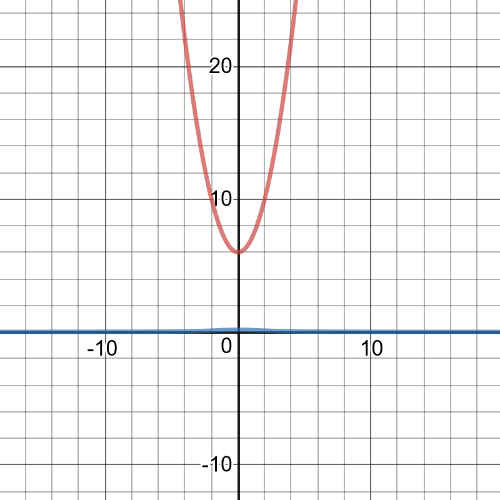
$textbf{The domain and range}$ are the same set, $D=R=Bbb{R}$;

$x$-intercepts is $x=-2$

This function is $textbf{negative}$ on interval $(-2,+infty)$ and $textbf{positive}$ on interval $(-infty,-2)$;

It is always $textbf{decreasing}$.

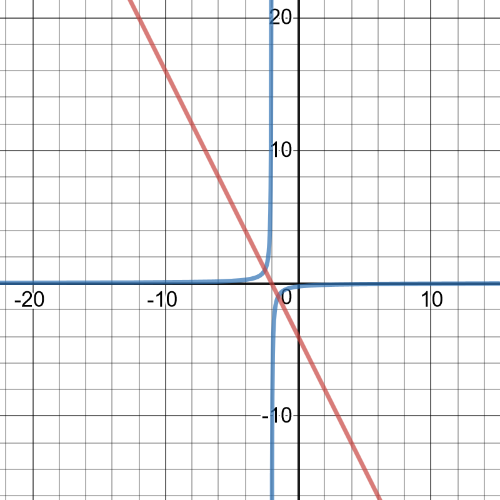
$textbf{The equation of reciprocal function}$ is $y=dfrac{1}{-2x-4}$ and on following graph are original function and reciprocal:

For example, let’s take function $f(x)=dfrac{p(x)}{q(x)}$ which we will analyse:

(1) $textbf{Hole}$, at $x=b$ if $dfrac{p(b)}{q(b)}=dfrac{0}{0}$;

(2) $textbf{Vertical asymptote}$ at $x=b$ if $dfrac{p(b)}{q(b)}=dfrac{p(b)}{0}$;

(3) $textbf{Horizontal asymptote}$ when the degree of $p(x)$ is less than or equal to the degree of $q(x)$;

(4) $textbf{Oblique asymptote}$ only when the degree of $p(x)$ is greater than the degree of $q(x)$ by exactly $1$.

#### (a)

We can conclude that this function has $textbf{vertical asymptote}$ at $x=2$ and $textbf{horizontal asymptote}$ at $y=1$.
#### (b)

This function has $textbf{hole}$ at $x=1$ because of:

$y=dfrac{x-1}{3x-3}=dfrac{x-1}{3(x-1)}=dfrac{1}{3}$, $xne1$
#### (c)

We can conclude that this function has $textbf{vertical asymptote}$ at $x=-dfrac{1}{2}$ and $textbf{horizontal asymptote}$ at $y=-dfrac{7}{4}$.
#### (d)

We can conclude that this function has $textbf{vertical asymptote}$ at $x=6$ and $textbf{oblique asymptote}$ because degree of the expression in the numerator is larger than the expression in the denominator for $1$.
#### (e)

We can conclude that this function has $textbf{vertical asymptotes}$ at $x=-5$ and $x=3$ $textbf{horizontal asymptote}$ at $y=0$, because:

$$
y=dfrac{1}{x^2+2x-15}=dfrac{1}{(x+5)(x-3)}
$$

(a) horizontal asymptote at $y=1$ and vertical at $x=2$;

(b)hole at $x=1$;

(c)horizontal asymptote at $y=-dfrac{7}{4}$ and vertical at $x=-dfrac{1}{2}$;

(d)vertical asymptote at $x=6$ and oblique asymptote;

(e)horizontal asymptote at $y=0$ and vertical at $x=-5$ and $x=3$

$textbf{Horizontal asymptotes}$ had functions at parts (a) (c) and (e).

At part (a) it was a function $y=dfrac{x}{x-2}$ and equation of its $textbf{horizontal asymptote}$ is $y=1$.

At part (c) it was a function $y=dfrac{-7x}{4x+2}$ and equation of its $textbf{horizontal asymptote}$ is $y=-dfrac{7}{4}$.

At part (e) it was a function $y=dfrac{1}{x^2+2x-15}$ and equation of its $textbf{horizontal asymptote}$ is $y=0$.

$y=dfrac{x}{x-2}$, $y=1$; $y=dfrac{-7x}{4x+2}$, $y=-dfrac{7}{4}$; $y=dfrac{1}{x^2+2x-15}$, $y=0$.

#### (a)

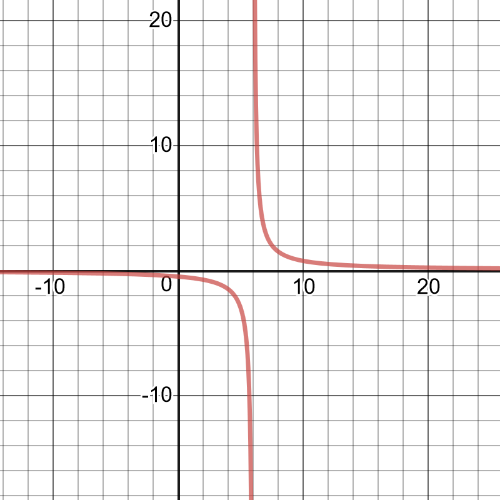
$textbf{Domain}$ of this function is set $D=left{xinBbb{R}|xne6 right}$;

$textbf{Vertical asymptote}$ is at $x=6$ and $textbf{horizontal}$ is at $y=0$;

This function is $textbf{positive}$ on interval $(6,+infty)$ and $textbf{negative}$ on $(-infty,6)$;

This function is always $textbf{decreasing}$ ;

$x$-intercept is point $(5,0)$ and $y$-intercept is point $(0,-dfrac{5}{6})$

On the following picture is its $textbf{graph}$:

#### (b)

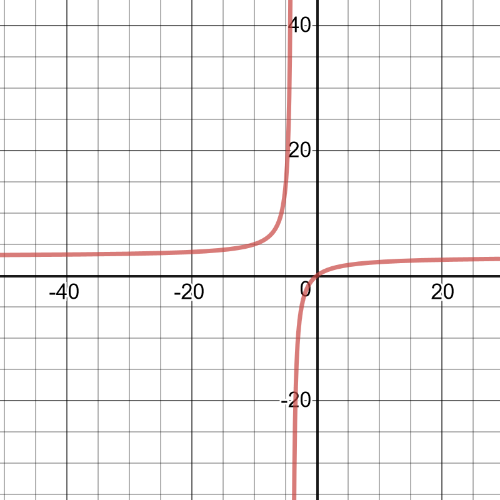
$textbf{Domain}$ of this function is set $D=left{xinBbb{R}|xne-4 right}$;

$textbf{Vertical asymptote}$ is at $x=-4$ and $textbf{horizontal}$ is at $y=3$;

This function is $textbf{positive}$ on interval $(-infty,-4)$ and $(0,+infty)$ $textbf{negative}$ on $(-4,0)$;

This function is always $textbf{increasing}$ ;

$x$-intercept and $y$-intercept is point $(0,0)$;

On the following picture is its $textbf{graph}$:

#### (c)

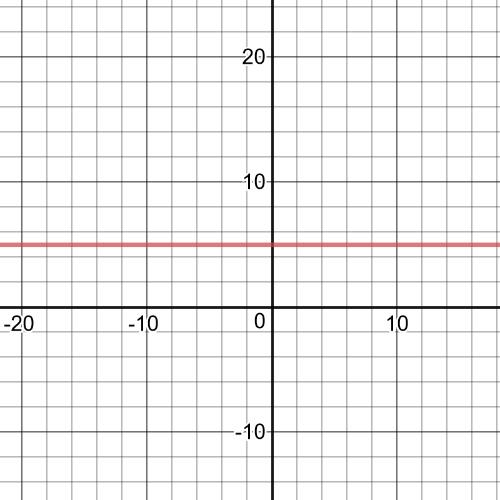
$textbf{Domain}$ of this function is set $D=left{xinBbb{R}|xne-2 right}$;

It has $textbf{a hole}$ at $x=-2$;

This function is always $textbf{positive}$;

On the following picture there is a $textbf{graph}$ of this function:

#### (d)

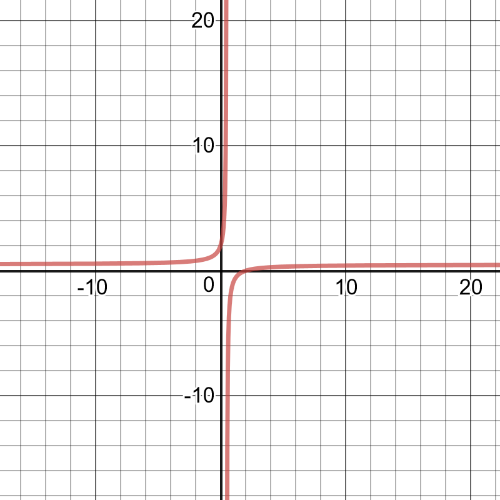
$textbf{Domain}$ of this function is set $D=left{xinBbb{R}|xnedfrac{1}{2} right}$;

$textbf{Vertical asymptote}$ is at $x=dfrac{1}{2}$ and $textbf{horizontal}$ is at $y=-dfrac{1}{2}$;

This function is $textbf{positive}$ on interval $(-infty,dfrac{1}{2})$ and on $(2,+infty)$ and $textbf{negative}$ on $(dfrac{1}{2},2)$;

This function is always $textbf{increasing}$ ;

$x$-intercept is point $(2,0)$ and $y$-intercept is point $(0,5)$;

On the following picture is its $textbf{graph}$:

First, function $y=dfrac{7x+6}{x}$ has $textbf{horizontal asymptote}$ at $y=7$ and $textbf{vertical asymptote}$ at $x=0$, it has $x$-intercept at point $(-dfrac{6}{7},0)$ and is always $textbf{decreasing}$.

Function $y=dfrac{7x+6}{x+1}$ has $textbf{horizontal asymptote}$ at $y=7$ and $textbf{vertical asymptote}$ at $x=-1$, it has $x$-intercept at point $(-dfrac{6}{7},0)$ and $y$-intercept at point $(0,6)$ and it is always $textbf{increasing}$.

And those two functions will not give him the same result because one is always decreasing and the other one is incresing, this means that those functions has different behaviour at their ends, for large values of $x$.

We will calculate value for $n$ from condition in task that function $f(x)$ has $textbf{vertical asymptote}$ at $x=6$, it means next:

$2-ncdot6=0$ $Rightarrow$ $6cdot{n}=2$ $Rightarrow$ $n=dfrac{2}{6}=dfrac{1}{3}$

Value for $m$ we will calculate from condition in task that $x$-intercept is point $(5,0)$:

$0=f(5)=dfrac{7cdot5-m}{2-dfrac{1}{3}cdot5}=dfrac{35-m}{2-dfrac{1}{3}cdot5}$ $Rightarrow$ $35-m=0$ $Rightarrow$ $m=35$

$n=dfrac{1}{3}$, $m=35$

According to conditions in task, it suppoused to be hole at $x=-2$, so, it may be function:

$y=dfrac{4x+8}{x+2}$

This function has domain like in task, has no vertical asymptote, has a hole at $x=-2$ and has vertical asymptote at $y=4$.

$y=dfrac{4x+8}{x+2}$