#### (a)

Here we have next:

$$
begin{align*}
x^2-3x-10&=x^2+4x+4-7x-14\&=(x+2)^2-7(x+2)\&=(x+2)(x+2-7)\&=(x+2)(x-5)
end{align*}
$$

#### (b)

$$
begin{align*}
3x^2+12x-15&=3(x^2+4x-5)\&=3(x^2+4x+4-9)\&=3((x+2)^2-9)\&=3((x+2)-3)((x+2)+3)\&=3(x-1)(x+5)
end{align*}
$$

#### (c)

$$
begin{align*}
16x^2-49=(4x-7)(4x+7)
end{align*}
$$

#### (d)

$$
9x^2-12x+4=(3x-2)^2
$$

#### (e)

By solving this quadriatic equation where unknown is $a$, we have:

$$
3a^2+a-30=(a-3)(a+dfrac{10}{3})
$$

#### (f)

By solving this quadriatic equation where unknown is $x$, we have:

$$
6x^2-5xy-21y^2=(x-dfrac{7}{3}y)(x+dfrac{3}{2}y)
$$

(a) $(x+2)(x-5)$; (b) $3(x-1)(x+5)$; (c) $(4x-7)(4x+7)$; (d) $(3x-2)^2$; (e) $(a-3)(a+dfrac{10}{3})$; (f) $(x-dfrac{7}{3}y)(x+dfrac{3}{4}y)$

#### (a)

$$
dfrac{12-8s}{4}=dfrac{4(3-2s)}{4}=3-s
$$

#### (b)

$dfrac{6m^2n^4}{18m^3n}=dfrac{n^3}{3m}$, $m,nne0$
#### (c)

$dfrac{9x^3-12x^2-3x}{3x}=dfrac{3x(3x^2-4x-1)}{3x}=3x^2-4x-1$, $xne0$
#### (d)

$dfrac{25x-10}{5(5x-2)^2}=dfrac{5(5x-2)}{5(5x-2)^2}=dfrac{1}{5x-2}$, $xnedfrac{2}{5}$
#### (e)

$dfrac{x^2+3x+8}{9-x^2}=dfrac{(x-3)(x+6)}{(3-x)(3+x)}=-dfrac{(3-x)(x+6)}{(3-x)(3+x)}=-dfrac{x+6}{x+3}$, $xnepm3$
#### (f)

$dfrac{a^2+4ab-5b^2}{2a^2+7ab-15b^2}=dfrac{(a-b)(a+5b)}{(a-dfrac{3}{2}b)(a+5b)}=dfrac{a-b}{a-dfrac{3}{2}b}$, $anedfrac{3}{2}b$

(a) $3-s$; (b) $dfrac{n^3}{3m}$; (c) $3x^2-4x-1$; (d) $dfrac{1}{5x-2}$; (e) $-dfrac{x+6}{x+3}$; (f) $dfrac{a-b}{a-dfrac{3}{2}b}$

#### (a)

$$
dfrac{3}{5}timesdfrac{7}{9}=dfrac{7}{15}
$$

#### (b)

$dfrac{2x}{5}divdfrac{x^2}{15}=dfrac{2x}{5}timesdfrac{15}{x^2}=dfrac{6}{x}$, $xne0$
#### (c)

$$
begin{align*}
dfrac{x^2-4}{x-3}divdfrac{x+2}{12-4x}&=dfrac{x^2-4}{x-3}timesdfrac{12-4x}{x+2}\&=dfrac{(x-2)(x+2)}{x-3}timesdfrac{4(3-x)}{x+2}\&=-4(x-2), xne3,-2
end{align*}
$$

#### (d)

$dfrac{x^3+4x^2}{x^2-1}timesdfrac{x^2-5x+6}{x^2-3x}=dfrac{x^2(x+4)}{(x-1)(x+1)}timesdfrac{(x-2)(x-3)}{x(x-3)}=dfrac{x(x+4)(x-2)}{(x-1)(x+1)}$

$$
xnepm1,0,3
$$

(a) $dfrac{7}{15}$; (b) $dfrac{6}{x}$; (c) $-4(x-2)$; (d) $dfrac{x(x+4)(x-2)}{(x-1)(x+1)}$

#### (a)

$$
dfrac{2}{3}+dfrac{6}{7}=dfrac{2cdot7+6cdot7}{21}=dfrac{56}{21}
$$

#### (b)

$$
dfrac{3x}{4}+dfrac{5x}{6}=dfrac{3cdot3x+2cdot5x}{12}=dfrac{19x}{12}
$$

#### (c)

$dfrac{1}{x}+dfrac{4}{x^2}=dfrac{x+4}{x^2}$, $xne0$
#### (d)

$dfrac{5}{x-3}-dfrac{2}{x}=dfrac{5x-2(x-3)}{x(x-3)}=dfrac{5x-2x+6}{x(x-3)}=dfrac{3x+6}{x(x-3)}=dfrac{3(x+2)}{x(x-3)}$, $xne0,3$
#### (e)

$dfrac{2}{x-5}+dfrac{y}{x^2-25}=dfrac{2}{x-5}+dfrac{y}{(x-5)(x+5)}=dfrac{2(x-5)+y}{(x-5)(x+5)}$, $xnepm5$
#### (f)

$dfrac{6}{a^2-9a+20}-dfrac{8}{a^2-2a-15}=dfrac{6}{(x-5)(x-4)}-dfrac{8}{(x-6)(x+2)}=dfrac{6(x-6)(x+2)-8(x-5)(x-4)}{(x-4)(x-5)(x-6)(x+2)}$,

$xne-2,4,5,6$

(a) $dfrac{56}{21}$; (b) $dfrac{19x}{12}$; (c) $dfrac{x+4}{x^2}$; (d) $dfrac{3(x+2)}{x(x-3)}$; (e) $dfrac{2(x-5)+y}{(x-5)(x+5)}$; (f) $dfrac{6(x-6)(x+2)-8(x-5)(x-4)}{(x-4)(x-5)(x-6)(x+2)}$

#### (a)

$dfrac{5x}{8}=dfrac{15}{4} /cdot8$

$5x=15cdot2=30$

$x=dfrac{30}{5}=6$

$textbf{Check:}$

$$
dfrac{5cdot6}{8}=dfrac{30}{8}=dfrac{15}{4}
$$

#### (b)

$dfrac{x}{4}+dfrac{1}{3}=dfrac{5}{6}$

$dfrac{3x+4}{12}=dfrac{5}{6} /cdot12$

$3x+4=10$

$3x=10-4=6$

$x=dfrac{6}{3}=2$

$textbf{Check:}$

$$
dfrac{2}{4}+dfrac{1}{3}=dfrac{1}{2}+dfrac{1}{3}=dfrac{3+2}{6}=dfrac{5}{6}
$$

#### (c)

$dfrac{4x}{5}-dfrac{3x}{10}=dfrac{3}{2} /cdot10$

$8x-3x=15$

$5x=15$

$x=dfrac{15}{5}=3$

$textbf{Check:}$

$$
dfrac{4cdot3}{5}-dfrac{3cdot3}{10}=dfrac{12}{5}-dfrac{9}{10}=dfrac{24-9}{10}=dfrac{15}{10}=dfrac{3}{2}
$$

#### (d)

$dfrac{x+1}{2}-dfrac{2x-1}{3}=-1 /cdot6$

$3(x+1)-2(2x-1)=-6$

$3x+3-4x+2=-6$

$-x+5=-6$

$-x=-6-5=-11$

$x=11$

$textbf{Check:}$

$$
dfrac{11+1}{2}-dfrac{2cdot11-1}{3}=dfrac{12}{2}-dfrac{21}{3}=6-7=-1
$$

(a) $x=6$; (b) $x=2$; (c) $x=3$; (d) $x=11$

On the following picture is $textbf{the graph}$ of the function $f(x)=dfrac{1}{x}$:

$textbf{The domain}$ of this function is set $D=left{xinBbb{R}|xne0 right}$ and $textbf{range}$ is also set $R=left{xinBbb{R}|xne0 right}$.This function is $textbf{odd}$ and it is $textbf{decreasing}$ on $(0,+infty)$ and it is $textbf{increasing}$ on interval $(-infty,0)$.This function $textbf{has vertical and horizontal asymptotes}$, and their equations are $x=0$ for vertical and $y=0$ for horizontal asymtote.

#### (a)

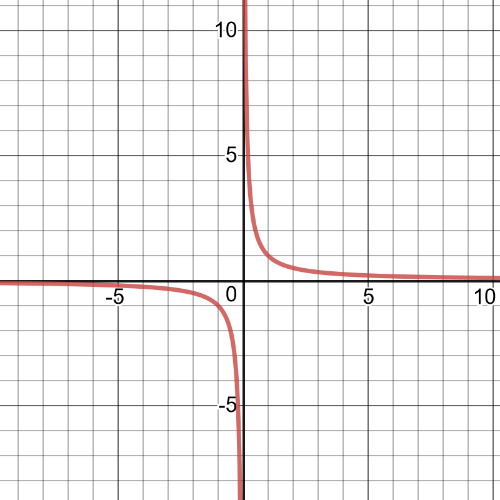
Here we have $textbf{translation}$ $3$ units to the left and on the following picture is graph of this transformed function:

#### (b)

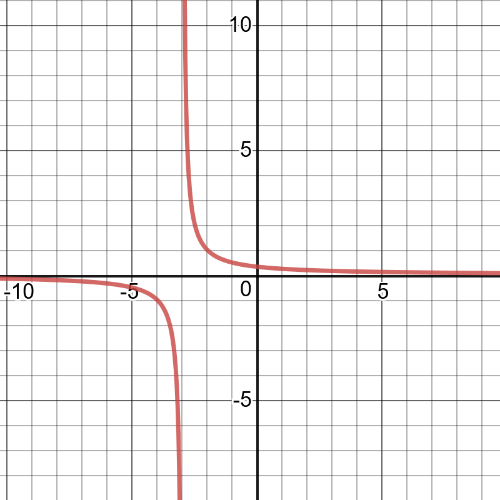
Here we have $textbf{vertical compression}$ by a factor of $2$ and $textbf{translation}$ $1$ unit to the right.On the following picture is graph of this transformed function:

#### (c)

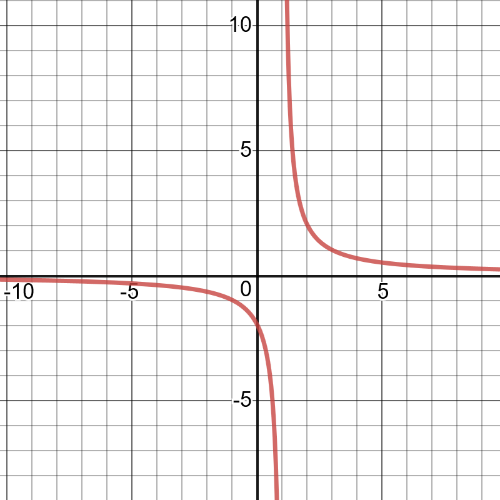
Here we have $textbf{vertical compression}$ by a factor of $-dfrac{1}{2}$ and $textbf{translation}$ $3$ units down.On the following picture is the graph of transformed function:

#### (d)

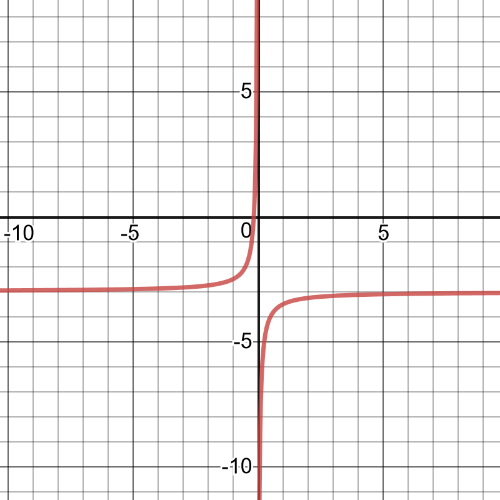
Here we have $textbf{vertical compression}$ by a factor of $2$ and $textbf{horizontal compression}$ by a factor of $-dfrac{1}{3}$, $textbf{translation}$ $2$ units to the right and $1$ unit up.On the following picture is graph oh transformed function:

When dividing two fractions, the first one does not work and the other is transformed by replacing the places with the numerator and the importer, and in the transformation of the second fraction thus performed, then the two fractions are multiplied.

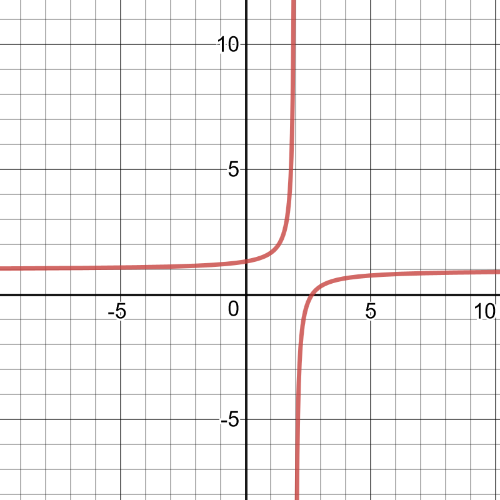
According to this, we will simplify following expression:

$$
begin{align*}
dfrac{9y^2-4}{4y-12}divdfrac{9y^2+12y+4}{18-6y}&=dfrac{9y^2-4}{4y-12}timesdfrac{18-6y}{9y^2+12y+4}\&=dfrac{(3y-2)(3y+2)}{4(y-3)}timesdfrac{6(3-y)}{(3y+2)^2}\&=-dfrac{3(3y-2)}{2(3y+2)}
end{align*}
$$

$-dfrac{3(3y-2)}{2(3y+2)}$