Determine the solution for each of the following.

$$
color{#4257b2}text{(a)} 0=-2x^3(2x-5)(x-4)^2
$$

$$
0=-2x^3 (2x-5)(x-4)(x-4)
$$

Use zero property as follows:

$$
-2x^3=0 x=0
$$

$$
2x-5=0 2x=5 x=dfrac{5}{2}
$$

$$
x-4=0 x=4
$$

$$
x=0, x=dfrac{5}{2}, x=4
$$

$$
color{#4257b2}text{(b)} 0=(x^2+1)(2x-4)(x+2)
$$

Use zero property as follows:

$$
x^2+1=0 x^2=-1 text{No solution}
$$

$$
2x-4=0 2x=4 x=2
$$

$$
x+2=0 x=-2
$$

$$
x=text{No solution}, x=2, x=-2
$$

$$
color{#4257b2}text{(c)} x^3-4x^2=7x-10
$$

Isolate the variables on the left side as follows:

$$
x^3-4x^2-7x=-10
$$

Use GFC as follows:

$$
x(x^2-4x-7)=-10 x(x+1.33)(x-5.33)=-10
$$

Use zero property as follows:

$$
x=-10
$$

$$
x+1.33=-10 x=-10-1.33 x=-11.33
$$

$$
x-5.33=-10 x=-10+5.33 x=-4.67
$$

$$
x=-10, x=-11.33, x=-4.67
$$

$$
color{#4257b2}text{(d)} 0=(x^2-2x-24)(x^2-25)
$$

Use completing square property as follows:

$$
0=(x+4)(x-6)(x-5)(x+5)
$$

Use zero property as follows:

$$
x+4=0 x=-4
$$

$$
x-6=0 x=6
$$

$$
x-5=0 x=5
$$

$$
x+5=0 x=-5
$$

$$
x=-4, x=6, x=5, x=-5
$$

$$
color{#4257b2}text{(e)} 0=(x^3+2x^2)(x+9)
$$

Use zero property as follows:

$$
x^3+2x^2=0
$$

Divided both of sides by $(x^2)$ as follows:

$$
x+2=0 x=-2
$$

$$
x+9=0 x=-9
$$

$$
x=-2, x=-9
$$

$$
color{#4257b2}text{(f)} -x^4=-13x^2+36
$$

Isolate the variables on the left side as follows:

$$
-x^4+13x^2-36=0
$$

$$
(x^2-4)(x^2-9)=0
$$

$$
(x-2)(x+2)(x-3)(x+3)=0
$$

Use zero property as follows:

$$
x-2=0 x=2
$$

$$
x+2=0 x=-2
$$

$$
x-3=0 x=3
$$

$$
x+3=0 x=-3
$$

$$
x=-2, x=2, x=-3, x=3
$$

$$
text{color{Brown}(a) $x=0, x=dfrac{5}{2}, x=4$
\ \
(b) $x=text{No solution}, x=2, x=-2$
\ \
(c) $x=-10, x=-11.33, x=-4.67$
\ \
(d) $x=-4, x=6, x=5, x=-5$
\ \
(e) $x=-2, x=-9$
\ \
(f) $x=-2, x=2, x=-3, x=3$}
$$

Jude is diving from a cliff into the ocean. His height above the sea level in meter is represented by $(h(t)=-5(t-0.3)^2+25$), $(t)$ measured time in second. Answer for the following questions.

$text{color{#4257b2}(a) Expand the function}$

$$
h(t)=-5(t-0.3)^2+25
$$

Separate the completing square as follows:

$$
h(t)=-5(t^2-0.6t+0.09)+25
$$

Use distributive property as follows:

$$
h(t)=-5t^2-3t-0.45+25 h(t)=-5t^2-3t+24.55
$$

$$
text{color{#4257b2}(b) How high is the cliff?}
$$

The high of the cliff is equal when the time is zero as follows:

$$
h(t)=-5(0)^2-3(0)+24.55 h(t)=0-0+24.55
$$

$$
h(t)=24.55 text{meter}
$$

$$
text{color{#4257b2}(c) When does Jude hit the water?}
$$

$$
h(t)=-5t^2-3t+24.55
$$

Use Quadrant equation of $left[x=dfrac{-bpmsqrt{b^2-4a c}}{2a}right]$ as follows:

$$
a=-5 b=-3 c=24.55
$$

$$
x=dfrac{3pmsqrt{(-3)^2-(4cdot-5cdot24.55)}}{2cdot-5} x=dfrac{3pmsqrt{9+491}}{-10}
$$

$$
x=dfrac{3+sqrt{500}}{-10} x=dfrac{3-sqrt{500}}{-10}
$$

$$
x=-2.536 text{second} x=1.936 text{second}
$$

The negative value of time is no reality, so the correct value of time equal $(1.936)$ second.

Jude hit the water after $(1.936)$ second

$$
text{color{#4257b2}(d) Determine where the function is negative value?}
$$

The function is negative when the time value is equal $(-2.536)$ second

$$
text{color{Brown}(a) $h(t)=-5t^2-3t+24.55$
\ \
(b) $h(t)=24.55 text{meter}$
\ \
(c) Jude hit the water after $(1.936)$ second
\ \
(d) The function is negative when the time value is equal $(-2.536)$ second}
$$

$$
text{color{#4257b2}Chris makes an open topped box from a $(30)$ cm by $(30)$ cm cardboard by cutting outs square equals from the corner. Calculate the dimensions of the box with a volume of $(1000)$ cm$^3$}
$$

Volume of resulting box can be represented by the following expression:

$$
V(x)=x(30-2x)(30-2x) V(x)=x (30-2x)^2
$$

Use distributive property as follows:

$$
1000=x[900-120x+4x^2] V(x)=4x^3-120x^2+900x=1000
$$

$$
{V}'(x)=12x^2-240x+900=0
$$

Divide the entire equation by $(12)$ as follows:

$$
x^2-20x+75=0
$$

Find a pair of number that have a $(75)$ and sum of $(-20)$ as ollows:

$$
(x-5)(x-15)=0
$$

$$
x-5=0 x=5 x-15=0 x=15
$$

Use zero property to find the range value of $(x)$ as follows:

$$
30-2x>0 -2x>-30 x<15
$$

According these ranges values of $(x)$, the matched value of $(x)$ is equal, $(5)$

The dimensions of box are:

Height, $=5$ cm Length, $=30-2(5)=20$ cm Width, $=30-2(5)=20$ cm

$$
text{color{Brown}Height $=5$ cm Length $=20$ cm Width $=20$ cm}
$$

Solve the following inequalities and graph it on number line.

$$
color{#4257b2}text{(a)} 2x-4<3x+7
$$

Isolate the variables on the left side as follows:

$$
2x-3x<7+4 -x-11
$$

$$
color{#4257b2}text{(b)} -x-4le x+4
$$

Isolate the variables on the left side as follows:

$$
-x-xle4+4 -2xle8
$$

Divide entire inequality by $(-2)$ as follows:

$$
xge-4
$$

$$
color{#4257b2}text{(c)} -2(x-4)ge16
$$

Use distributive property as follows:

$$
-2x+8ge16
$$

Isolate the variables on the left side as follows:

$$
-2xge16-8 -2xge8
$$

Divide entire inequality by $(-2)$ as follows:

$$
xle-4
$$

$$
color{#4257b2}text{(d)} 2(3x-7)>3(7x-3)
$$

Use distributive property as follows:

$$
6x-14>21x-9
$$

Isolate the variables on the left side as follows:

$$
6x-21x>-9+14 -15x>5
$$

Divide entire inequality by $(-15)$ as follows:

$$
x<-dfrac{1}{3}
$$

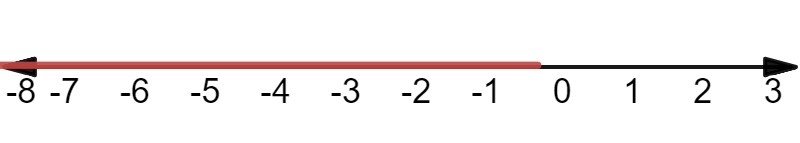
$$
text{color{Brown}(a) $x>-11$ (b) $xge-4$
\ \
(c) $xle-4$ (d) $x<-dfrac{1}{3}$}
$$

Solve the following inequalities.

$$
color{#4257b2}2x<dfrac{3x+6}{2}le4+2x
$$

Multiply entire inequality by $(2)$ as follows:

$$
4x<3x+6le8+4x
$$

Add inequality by $(-6)$ as follows:

$$
4x-6<3xle8+4x-6 4x-6<3xle4x+2
$$

Add inequality by $(-4x)$ as follows:

$$
4x-4x-6<3x-4xle4x-4x+2 -6xge-2
$$

$color{#4257b2}diamond Note that: Dividing by a negative number reverses the inequality sign.$

$therefore$ The solution set is $left[-2, 6 right)$

$$
text{color{Brown} $ [-2, 6)$}
$$

Create a linear inequality for the following solution.

$$
color{#4257b2}text{(a)} x>7
$$

$$
2(2x-3)>3x+1
$$

$$
color{#4257b2}text{(b)} xin (-infty, -8)
$$

$$
2x-4>3x+12
$$

$$
color{#4257b2}text{(c)} -1le xle7
$$

$$
2x-5le 3x-4le2x+3
$$

$$
color{#4257b2}text{(d)} [3, 8)
$$

$$
x+1le2x-2<6+x
$$

$$
text{color{Brown}(a) $2(2x-3)>3x+1$ (b) $2x-4>3x+12$
\ \
(c) $2x-5le 3x-4le2x+3$ (d) $x+1le2x-2<6+x$}
$$

Consider the graph in the textbook, then answer for the following questions.

$$
text{color{#4257b2}(a) Write the equations that modelled by the graph.}
$$

$$
f(x)=-x+1 g(x)=2x-5
$$

$$
text{color{#4257b2}(b) Solve the inequality of $f(x)<g(x)$ by examining the graph.}
$$

$$
-x+1<2x-5 text{From the graph} 1<dfrac{5}{2}
$$

$$
text{color{#4257b2}(c) Confirm your solution by solve the inequality algabrically.}
$$

For equation of, $(f(x)=-x+1)$

$$
-x+1=0 x=1
$$

For equation of, $(g(x)=2x-5)$

Use zero property as follows:

$$
2x-5=0 2x=5 x=dfrac{5}{2}
$$

$$
text{color{Brown}(a) $f(x)=-x+1 g(x)=2x-5$
\ \
(b) $1<dfrac{5}{2}$ (c) $x=1 x=dfrac{5}{2}$}
$$

The network cell phone company charges $(20)$ dollar per month and $(0.02)$ dollar per minute

My mobile company charges $(15)$ dollar per month and $(0.03)$ dollar per minute. Answer for the following question.

$$
text{color{#4257b2}(a) Write the expression for the total bill for each company}
$$

Network company$a_n=20+0.02n$, where, $(n)$, call minutes

My company$a_n=15+0.03n$, where, $(n)$, call minutes

$$
text{color{#4257b2}(b) Set the inequality represent for what amount of time in minutes, my mobile is better plan }
$$

$$
20+0.02n>15+0.03n
$$

$$
text{color{#4257b2}(c) Solve the inequality}
$$

Isolate the variables on the left side as follows:

$$
0.02n-0.03n>15-20 -0.01n>-5
$$

Divide both of sides by $(-0.01)$ as follows:

$$
n<500
$$

My mobile is better plan when number of minute less than $(500)$ minute as per inequality $(n<500)$

$$
text{color{#4257b2}(d) Why did you put a restriction in algebraic solution }
$$

to get the best value of call minutes for my mobile company.

$$
text{color{Brown}(a) $a_n=20+0.02n$ $a_n=15+0.03n$
\ \
(b) $20+0.02n>15+0.03n$ (c) $n<500$
\ \
To get the best value of call minutes for my mobile company.}
$$