
All Solutions
Page 213: Check Your Understanding
$$
3x-1 leq 11
$$
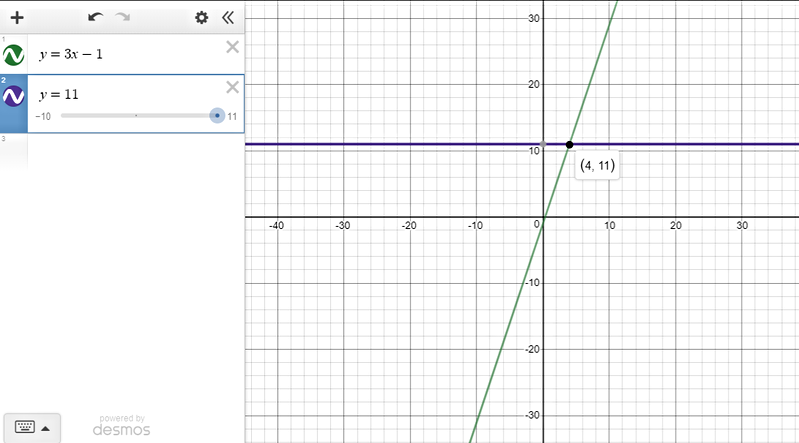
$text{underline{Step 1:}}$ Graph each side of the inequality as a function.
The y-values on the line $color{#4257b2}y=3x-1$ that are less than or equal $color{#4257b2}11$ are found on all points that lie on the line below the horizontal line $color{#4257b2}y=11$.
$text{underline{Step 2:}}$ This happens when $color{#4257b2}x leq 4$ (we get the $x$ value from the intersection of the two lines.)
$$
text{color{#4257b2}$therefore$ The solution set is $(-infty, 4]$}
$$
$$
-x+5 > -2
$$
Multiply each side by $(-1)$
$$
x-5 < 2
$$
$color{#4257b2}diamond Note that: Multiply by a negative number reverses the inequality sign.$
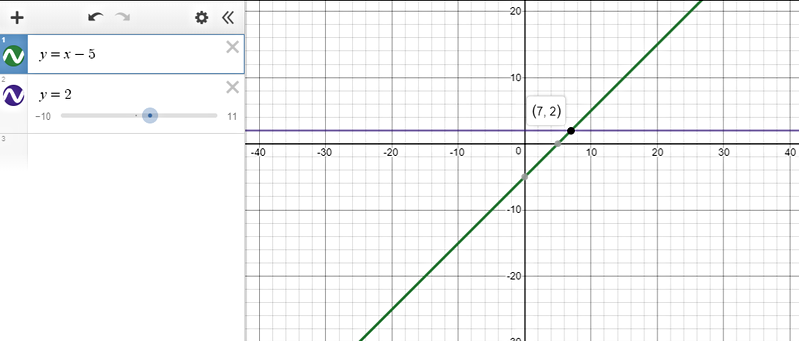
$text{underline{Step 1:}}$ Graph each side of the inequality as a function.
The y-values on the line $color{#4257b2}y=x-5$ that are less than $color{#4257b2}2$ are found on all points that lie on the line below the horizontal line $color{#4257b2}y=2$.
$text{underline{Step 2:}}$ This happens when $color{#4257b2}x < 7$ (we get the $x$ value from the intersection of the two lines.)
$$
text{color{#4257b2}$therefore$ The solution set is $(-infty, 7)$}
$$
$$
x-2 > 3x+8
$$
Subtract $(3x)$ from each side
$$
-2x-2 > 8
$$
Multiply each side by $(-1)$
$$
2x+2 < -8
$$
$color{#4257b2}diamond Note that: Multiply by a negative number reverses the inequality sign.$
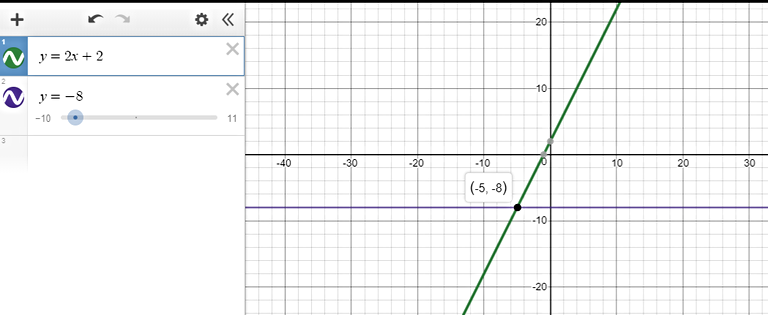
$text{underline{Step 1:}}$ Graph each side of the inequality as a function.
The y-values on the line $color{#4257b2}y=2x+2$ that are less than $color{#4257b2}-8$ are found on all points that lie on the line below the horizontal line $color{#4257b2}y=-8$.
$text{underline{Step 2:}}$ This happens when $color{#4257b2}x < -5$ (we get the $x$ value from the intersection of the two lines.)
$$
text{color{#4257b2}$therefore$ The solution set is $(-infty, -5)$}
$$
$$
3(2x+4) geq 2x
$$
Remove the brackets
$$
6x+12 geq 2x
$$
Subtract $(2x)$ from each side
$$
4x+12 geq 0
$$
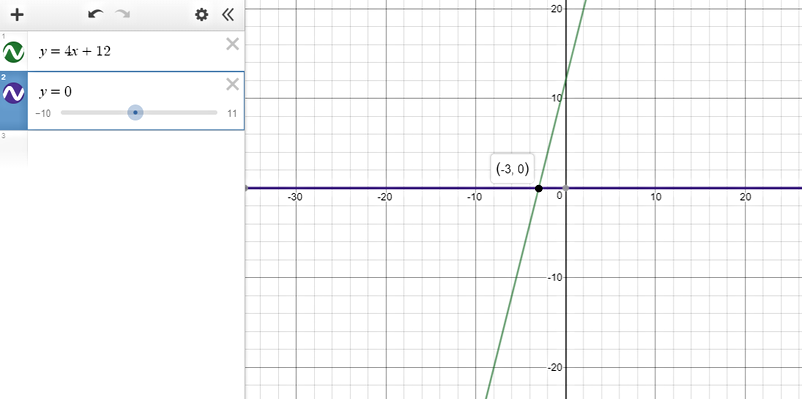
$text{underline{Step 1:}}$ Graph each side of the inequality as a function.
The y-values on the line $color{#4257b2}y=4x+12$ that are greater than or equal $color{#4257b2}0$ are found on all points that lie on the line below the horizontal line $color{#4257b2}y=0$.
$text{underline{Step 2:}}$ This happens when $color{#4257b2}x geq -3$ (we get the $x$ value from the intersection of the two lines.)
$$
text{color{#4257b2}$therefore$ The solution set is $[-3, infty)$}
$$
$$
-2(1-2x) < 5x+8
$$
Remove the brackets
$$
-2+4x < 5x+8
$$
Subtract $(5x)$ from each side
$$
-2-x -8
$$
$color{#4257b2}diamond Note that: Multiply by a negative number reverses the inequality sign.$
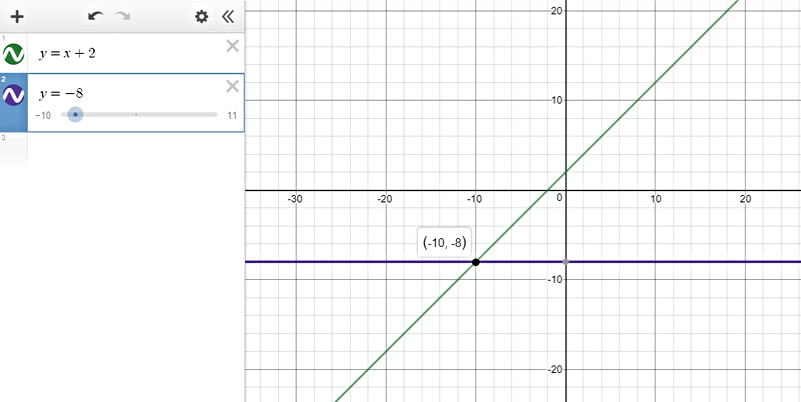
$text{underline{Step 1:}}$ Graph each side of the inequality as a function.
The y-values on the line $color{#4257b2}y=x+2$ that are greater than $color{#4257b2}-8$ are found on all points that lie on the line below the horizontal line $color{#4257b2}y=-8$.
$text{underline{Step 2:}}$ This happens when $color{#4257b2}x > -10$ (we get the $x$ value from the intersection of the two lines.)
$$
text{color{#4257b2}$therefore$ The solution set is $(-10, infty)$}
$$
$$
dfrac{6x+8}{5} leq 2x-4
$$
Multiply each side by $(5)$
$$
6x+8 leq 10x-20
$$
Subtract $(10x)$ from each side
$$
-4x+8 leq -20
$$
Multiply each side by $(-1)$
$$
4x-8 geq 20
$$
$color{#4257b2}diamond Note that: Multiply by a negative number reverses the inequality sign.$
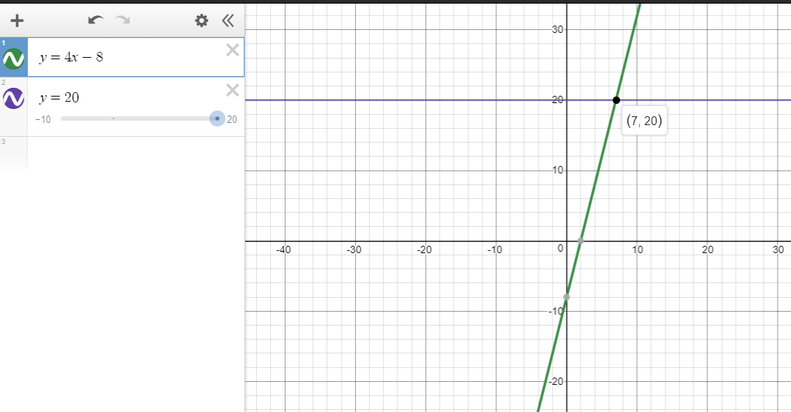
$text{underline{Step 1:}}$ Graph each side of the inequality as a function.
The y-values on the line $color{#4257b2}y=4x-8$ that are greater than or equal $color{#4257b2}20$ are found on all points that lie on the line below the horizontal line $color{#4257b2}y=20$.
$text{underline{Step 2:}}$ This happens when $color{#4257b2}x geq 7$ (we get the $x$ value from the intersection of the two lines.)
$$
text{color{#4257b2}$therefore$ The solution set is $[7, infty)$}
$$
text{color{Brown} (a) $left(-infty, 4 right]$ (b) $left(-infty, 7 right)$ (c) $left(-infty, -5 right)$ \ \
(d) $left[-3, infty right)$ (e) $left(-10, infty right)$ (f) $left[7, infty right)$}
$$
$$
2x-5 leq 4x+1
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
Now, we can subtract $(4x)$ from each side as follows:
$$
2x-5-4x leq 4x+1-4x
$$
$$
-2x-5 leq 1
$$
Then, add (5) to each side as follows:
$$
-2x-5+5 leq 1+5
$$
$$
-2x leq 6
$$
Then we will divide both sides by $(-2)$ in order to remove the $(-2)$ from the left side as follows:
$$
color{#4257b2}diamond Note that: Dividing by a negative number reverses the inequality sign.
$$
$$
dfrac{-2x}{-2} geq dfrac{6}{-2}
$$
$$
x geq -3
$$
$$
text{color{#4257b2}$therefore$ The solution set is $left[-3, infty right)$}
$$
$$
2(x+3) < -(x-4)
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a < b, text{then} a pm c < b pm c
$$
First, we will remove the brackets as follows:
$$
2x+6 < -x+4
$$
Then, subtract (6) from each side as follows:
$$
2x+6-6 < -x+4-6
$$
$$
2x < -x-2
$$
Then, add $(x)$ to each side as follows:
$$
2x+x < -x-2+x
$$
$$
3x < -2
$$
Then we will divide both sides by $(3)$ in order to remove the $(3)$ from the left side as follows:
$$
dfrac{3x}{3} < dfrac{-2}{3}
$$
$$
x < -dfrac{2}{3}
$$
$$
text{color{#4257b2}$therefore$ The solution set is $left(-infty, -dfrac{2}{3} right)$}
$$
$$
dfrac{2x+3}{3} leq x-5
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
First, multiply each side by $(3)$
$$
dfrac{2x+3}{3} cdot 3 leq (x-5) cdot 3
$$
$$
2x+3 leq 3x-15
$$
Now, we can subtract $(3x)$ from each side as follows:
$$
2x+3-3x leq 3x-15 -3x
$$
$$
-x+3 leq -15
$$
Then, subtract (3) from each side as follows:
$$
-x+3-3 leq -15-3
$$
$$
-x leq -18
$$
Then we will divide both sides by $(-1)$ in order to remove the $(-)$ from the left side as follows:
$$
color{#4257b2}diamond Note that: Dividing by a negative number reverses the inequality sign.
$$
$$
dfrac{-x}{-1} geq dfrac{-18}{-1}
$$
$$
x geq 18
$$
$$
text{color{#4257b2}$therefore$ The solution set is $left[18, infty right)$}
$$
$$
2x+1 leq 5x-2
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
Now, we can subtract $(5x)$ from each side as follows:
$$
2x+1-5x leq 5x-2-5x
$$
$$
-3x+1 leq -2
$$
Then, subtract (1) from each side as follows:
$$
-3x+1-1 leq -2-1
$$
$$
-3x leq -3
$$
Then we will divide both sides by $(-3)$ in order to remove the $(-3)$ from the left side as follows:
$$
color{#4257b2}diamond Note that: Dividing by a negative number reverses the inequality sign.
$$
$$
dfrac{-3x}{-3} geq dfrac{-3}{-3}
$$
$$
x geq 1
$$
$$
text{color{#4257b2}$therefore$ The solution set is $left[1, infty right)$}
$$
$$
-x+1 > x+1
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
Now, we can subtract $(x)$ from each side as follows:
$$
-x+1-x > x+1-x
$$
$$
-2x+1 > 1
$$
Then, subtract $(1)$ from each side as follows:
$$
-2x+1-1 > 1-1
$$
$$
-2x > 0
$$
Then we will divide both sides by $(-2)$ in order to remove the $(-2)$ from the left side as follows:
$$
color{#4257b2}diamond Note that: Dividing by a negative number reverses the inequality sign.
$$
$$
dfrac{-2x}{-2} < dfrac{0}{-2}
$$
$$
x < 0
$$
$$
text{color{#4257b2}$therefore$ The solution set is $left(-infty, 0 right)$}
$$
$$
dfrac{x+4}{2} geq dfrac{x-2}{4}
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
First, multiply each side by $(4)$
$$
4 cdot dfrac{x+4}{2} geq 4 cdot dfrac{x-2}{4}
$$
$$
2 (x+4) geq x-2
$$
$$
2x+8 geq x-2
$$
Then subtract $(x)$ from each side as follows:
$$
2x+8-x geq x-2-x
$$
$$
x+8 geq -2
$$
Then, subtract $(8)$ from each side as follows:
$$
x+8-8 geq -2-8
$$
$$
x geq -10
$$
$$
text{color{#4257b2}$therefore$ The solution set is $left[-10, infty right)$}
$$
text{color{Brown} (a) $left[-3, infty right)$ (b) $left(-infty, -dfrac{2}{3} right)$ (c) $left[18, infty right)$ \ \
(d) $left[1, infty right)$ (e) $left(-infty, 0 right)$ (f) $left[-10, infty right)$}
$$
$$
3 leq 2x+5 < 9
$$
$diamond$ Note that: The subtractionand addtion properties of inequalities state,
$$
color{#4257b2} text{If} a < b, text{then} a pm c < b pm c
$$
Now, we can subtract (5) from each side as follows:
$$
3-5 leq 2x+5-5 < 9-5
$$
$$
-2 leq 2x < 4
$$
Then we will divide all sides by $(2)$ as follows:
$$
dfrac{-2}{2} leq dfrac{2x}{2} < dfrac{4}{2}
$$
$$
-1 leq x < 2
$$
$$
text{color{#4257b2}$therefore$ The solution set is $[-1, 2)$}
$$

text{color{Brown} $[-1, 2)$}
$$
text{(a)} x > -1
$$
$because$ The solution set is $left(-1, infty right)$
$$
text{color{#4257b2}$therefore$ $x=2$ is contained in the solution set.}
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a < b, text{then} a pm c 3x+2-3x
$$
$$
2x-4 > 2
$$
Then, add $(4)$ to each side as follows:
$$
2x-4+4 > 2+4
$$
$$
2x > 6
$$
Then we will divide both sides by $(2)$ in order to remove the $(2)$ from the left side as follows:
$$
x > 3
$$
$therefore$ The solution set is $left(3, infty right)$
$$
text{color{#c34632}$therefore$ $x=2$ is not contained in the solution set.}
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a geq b, text{then} a pm c geq b pm c
$$
First, remove the brackets as follows:
$$
12x-20 geq 6x
$$
Then subtract $(6x)$ from each side as follows:
$$
12x-20-6x geq 6x-6x
$$
$$
6x-20 geq 0
$$
Then, add $(20)$ to each side as follows:
$$
6x-20+20 geq 0+20
$$
$$
6x geq 20
$$
Then we will divide both sides by $(6)$ in order to remove the $(6)$ from the left side as follows:
$$
x geq dfrac{20}{6}
$$
$therefore$ The solution set is $left[dfrac{20}{6}, infty right)$
$$
text{color{#c34632}$therefore$ $x=2$ is not contained in the solution set.}
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
Now, we can add $(3x)$ to each side as follows:
$$
5x+3+3x leq -3x+1+3x
$$
$$
8x+3 leq 1
$$
Then, subtract $(3)$ from each side as follows:
$$
8x+3-3 leq 1-3
$$
$$
8x leq -2
$$
Then we will divide both sides by $(8)$ in order to remove the $(8)$ from the left side as follows:
$$
dfrac{8x}{8} leq dfrac{-2}{8}
$$
$$
x leq -dfrac{1}{4}
$$
$therefore$ The solution set is $left(-infty, -dfrac{1}{4} right]$
$$
text{color{#c34632}$therefore$ $x=2$ is not contained in the solution set.}
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
Now, we can subtract $(x)$ from each part as follows:
$$
x-2-x leq 3x+4-x leq x+14-x
$$
$$
-2 leq 2x+4 leq 14
$$
Then, subtract $(4)$ from each part as follows:
$$
-2-4 leq 2x+4-4 leq 14-4
$$
$$
-6 leq 2x leq 10
$$
Then we will divide both sides by $(2)$ in order to remove the $(2)$ from the left side as follows:
$$
dfrac{-6}{2} leq dfrac{2x}{2} leq dfrac{10}{2}
$$
$$
-3 leq x leq 5
$$
$therefore$ The solution set is $left[-3, 5 right]$
$$
text{color{#4257b2}$therefore$ $x=2$ is contained in the solution set.}
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
Now, we can subtract $(3)$ from each part as follows:
$$
33-3 < -10x+3-3 < 54 -3
$$
$$
30 < -10x dfrac{-10x}{-10} > dfrac{51}{-10}
$$
$$
-3 > x > -5.1
$$
$color{#4257b2}diamond Note that: Dividing by a negative number reverses the inequality sign.$
$therefore$ The solution set is $left(-5.1, -3 right)$
$$
text{color{#c34632}$therefore$ $x=2$ is not contained in the solution set.}
$$
text{color{Brown} (a) $x=2$ is contained. (b) $x=2$ is not contained. \ \
(c) $x=2$ is not contained. (d) $x=2$ is not contained.\ \
(e) $x=2$ is contained. (f) $x=2$ is not contained.}
$$
$color{#4257b2}text{(a)} 2x-1le13$
Add both of side by $(1)$ as follows:
$$
2xle13+1 2xle14
$$
Divide both of sides by $(2)$ as follows:
$$
xle7
$$

Add both of side by $(1)$ as follows:
$$
-2x>-1+1 -2x>0
$$
Divide both of sides by $(-2)$ as follows:
$$
x<0
$$

Isolate the variables on the left side as follows:
$$
2x-4x>12+8 -2x>20
$$
Divide both of side by $(-2)$ as follows:
$$
x<-10
$$
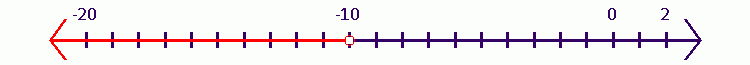
Use distributive property as follows:
$$
5x-15ge2x
$$
Isolate the variables on the left side as follows:
$$
5x-2xge15 3xge15
$$
Divide both of side by $(3)$ as follows:
$$
xge5
$$

Use distributive property as follows:
$$
-20+12x<6x+16
$$
Isolate the variables on the left side as follows:
$$
12x-6x<16+20 6x<36
$$
Divide both of side by $(6)$ as follows:
$$
x<6
$$

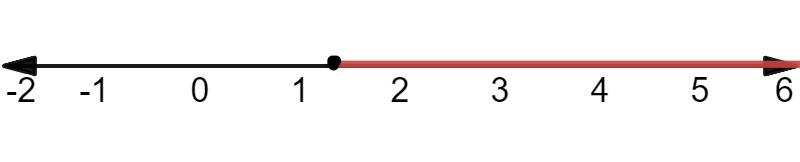
Use distributive property as follows:
$$
x-2le3(2x-3) x-2le6x-9
$$
Isolate the variables on the left side as follows:
$$
x-6xle-9+2 -5xle-7
$$
Divide both of side by $(-5)$ as follows:
$$
xgedfrac{7}{5} xge1.4
$$
text{color{Brown}(a) $ xleq 7$ (b) $x< 0$ (c) $x<-10$ \
(d) $ xgeq 5$ (e) $x < 6$ (f) $x geq dfrac{7}{5}$}
$$
$$
begin{align*}
3cdot0&le 4cdot0+1\
0&le 1.
end{align*}$$
Since $0$ is less than $1$, the inequality holds and $0$ is in the solution set of this inequality.
$$
begin{align*}
-6cdot0&<0+ 4<12\
0&< 4<12.
end{align*}$$
Since $0$ is less than $4$ and $4$ is less than 12, the inequality holds and $0$ is in the solution set of this inequality.
$$
begin{align*}
-0+1&>0+12\
0&>12.
end{align*}$$
Since $0$ is not greater than 12, the inequality does not hold and $0$ is not in the solution set of this inequality.
$$
begin{align*}
3cdot0&le0+1le0-1\
0&le 1le -1.
end{align*}$$
Since $0$ is less than $1$, but $1$ is not less than $-1$, the inequality does not hold and $0$ is not in the solution set of this inequality.
$$
begin{align*}
0cdot(2cdot0-1)&le07\
0&le 7.
end{align*}$$
Since $0$ is less than $7$, the inequality holds and $0$ is in the solution set of this inequality.
$$
begin{align*}
0+6&<(0+2)(5cdot0+3)\
6&< 6.
end{align*}$$
Since $6$ is equal, but not less than $6$, the inequality does not hold and $0$ is not in the solution set of this inequality.
b) Yes;
c) No;
d) No;
e)Yes;
d) No.
$$
-5 < 2x+7 < 11
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
Now, we can subtract $(7)$ from each side as follows:
$$
-5-7 < 2x+7-7 < 11-7
$$
$$
-12 < 2x < 4
$$
Then we will divide each side by $(2)$ as follows:
$$
-dfrac{12}{2} < dfrac{2x}{2} < dfrac{4}{2}
$$
$$
-6 < x < 2
$$
$$
text{color{#4257b2}$therefore$ The solution set is $left(-6, 2 right)$}
$$
$$
11 < 3x-1 < 23
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
Now, we will add $(1)$ to each side as follows:
$$
11+1 < 3x-1+1 < 23+1
$$
$$
12 < 3x < 24
$$
Then we will divide each side by $(3)$ follows:
$$
dfrac{12}{3} < dfrac{3x}{3} < dfrac{24}{3}
$$
$$
4 < x < 8
$$
$$
text{color{#4257b2}$therefore$ The solution set is $left(4, 8 right)$}
$$
$$
-1 leq -x+9 leq 13
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
Now, we will subtract $(9)$ from each side as follows:
$$
-1-9 leq -x+9-9 leq 13-9
$$
$$
-10 leq -x leq 4
$$
Then we will divide each side by $(-1)$ as follows:
$$
dfrac{-10}{-1} geq dfrac{-x}{-1} geq dfrac{4}{-1}
$$
$$
10 geq x geq -4
$$
$color{#4257b2}diamond Note that: Dividing by a negative number reverses the inequality sign.$
$$
text{color{#4257b2}$therefore$ The solution set is $left[-4, 10 right]$}
$$
$$
0 leq -2(x+4) leq 6
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
First, remove the brackets
$$
0 leq -2x-8 leq 6
$$
Then, we will add $(8)$ to each side as follows:
$$
0+8 leq -2x-8+8 leq 6+8
$$
$$
8 leq -2x leq 14
$$
Then we will divide each side by $(-2)$ as follows:
$$
dfrac{8}{-2} geq dfrac{-2x}{-2} geq dfrac{14}{-2}
$$
$$
-4 geq x geq -7
$$
$color{#4257b2}diamond Note that: Dividing by a negative number reverses the inequality sign.$
$$
text{color{#4257b2}$therefore$ The solution set is $left[-7, -4 right]$}
$$
$$
59 < 7x+10 < 73
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
Now, we can subtract $(10)$ from each side as follows:
$$
59-10 < 7x+10-10 < 73-10
$$
$$
49 < 7x < 63
$$
Then we will divide each side by $(7)$ as follows:
$$
dfrac{49}{7} < dfrac{7x}{7} < dfrac{63}{7}
$$
$$
7 < x < 9
$$
$$
text{color{#4257b2}$therefore$ The solution set is $left(7, 9 right)$}
$$
$$
18 leq -12(x-1) leq 48
$$
$diamond$ Note that: The subtraction and addtion properties of inequalities state,
$$
color{#4257b2} text{If} a leq b, text{then} a pm c leq b pm c
$$
First, remove the brackets
$$
18 leq -12x+12 leq 48
$$
Then, we will subtract $(12)$ from each side as follows:
$$
18-12 leq -12x+12-12 leq 48-12
$$
$$
6 leq -12x leq 36
$$
Then we will divide each side by $(-12)$ as follows:
$$
dfrac{6}{-12} geq dfrac{-12x}{-12} geq dfrac{36}{-12}
$$
$$
-dfrac{1}{2} geq x geq -3
$$
$color{#4257b2}diamond Note that: Dividing by a negative number reverses the inequality sign.$
$$
text{color{#4257b2}$therefore$ The solution set is $left[-3, -dfrac{1}{2} right]$}
$$
text{color{Brown} (a) $left(-6, 2 right)$ (b) $left(4, 8 right)$ (c) $left[-4, 10 right]$ \ \
(d) $left[-7, -4 right]$ (e) $left(7, 9 right)$ (f) $left[-3, -dfrac{1}{2} right]$}
$$
text{color{#4257b2}(a) Create a linear inequality for which the solution set is $x>4$}
$$
$$
-2x+5>9-3x
$$
Isolate the variables on the left side as follows:
$$
-2x+3x>9-5 x>4
$$
$$
text{color{#4257b2}(b) Create a linear inequality for which the solution set is $xledfrac{3}{2}$}
$$
$$
2(2x+3)ge3(2x+1)
$$
Use distributive property as follows:
$$
4x+6ge6x+3
$$
Isolate the variables on the left side as follows:
$$
4x-6xge3-6 -2xge-3
$$
Divide both of sides by $(-2)$ as follows:
$$
xledfrac{3}{2}
$$
text{color{Brown}(a) $-2x+5>9-3x$
\ \
(b) $2(2x+3)ge3(2x+1)$}
$$
$text{color{#4257b2} The solution set is $left{xmid -6 leq x leq 4 right}$}$
(a) We would like to create a double inequality for which this is the solution set.
$$
text{color{#4257b2} The double inequality is $( -6 leq x leq 4 )$}
$$
text{color{Brown} (a) The solution set is $left{xmid -6 leq x leq 4 right}$ \
(b) The double inequality is $( -6 leq x leq 4 )$}
$$
$$
text{color{#4257b2}For $x-3<3-x<x-5$}
$$
Add $(-x)$ for entire the inequality as follows:
$$
x-x-3<3-x-x<x-x-5 -3<3-2x<-5
$$
Add $(-3)$ for entire the inequality as follows:
$$
-3-3<3+3-2x<-5-3 -6<-2xx>4
$$
This inequality has a solution
$$
text{color{#4257b2}For $-3>3-x>x-5$}
$$
Add $(x)$ for entire the inequality as follows:
$$
-3+x>3-x+x>-5+x
$$
This inequality has no solution, due the variables on the tow sides of inequality.
text{color{Brown}The inequality which has a solution is $x-3<3-x<x-5$}
$$
$$
text{color{#4257b2}(a) Write the inequality that modelled by the graph.}
$$
$$
f(x)=3 xin R f(x)=dfrac{1}{2} x+1 x in R
$$
$$
text{color{#4257b2}(b) Find the solution by examining the graph.}
$$
From the graph, for $(y=3)$
Value of $(x=0)$ and $(x)$, values available for all real number. because the function is constant at $(y=3)$.
From the graph, for $left(y=dfrac{1}{2} x+1right)$
Value of $(x=-2)$
$$
text{color{#4257b2}(c) Confirm your solution by solve the inequality algabrically.}
$$
For equation of, $(y=3)$
Value of $(x=0)$ and $(x)$, values available for all real number. because the function is constant at $(y=3)$.
For equation of, $left(y=dfrac{1}{2} x+1right)$
Use zero property as follows:
$$
dfrac{1}{2} x+1=0 dfrac{1}{2} x=-1
$$
Multiply both of sides by $(2)$ as follows:
$$
x=-1cdot2 x=-2
$$
text{color{Brown}
(a) $f(x)=3 xin R f(x)=dfrac{1}{2} x+1 x in R$
\ \
(b) From the graph $x=0 x=-2$
\ \
(c) Solve algebraically $x=0 x=-2$}
$$
The temperature house between $18text{textdegree}$ and $22text{textdegree}$ Celsius
$$
text{color{#4257b2}(a) Write the double linear inequality}
$$
$$
18 text{textdegree} Cle xle22 text{textdegree} C
$$
$$
text{color{#4257b2}(b) Find the range of temperature in Fahrenheit degree.}
$$
For$18text{textdegree}$C
$$
C=dfrac{5}{9}(F-32) 18=dfrac{5}{9}(F-32)
$$
Multiply both of sides by $left(dfrac{9}{5}right)$ as follows:
$$
18cdotdfrac{9}{5}=F-32
$$
Isolate the variables on the only side as follows:
$$
F=dfrac{162}{5}+32 F=dfrac{160+162}{5}
$$
$$
F=dfrac{322}{5} F=64.4text{textdegree}text{F}
$$
$$
C=dfrac{5}{9}(F-32) 22=dfrac{5}{9}(F-32)
$$
Multiply both of sides by $left(dfrac{9}{5}right)$ as follows:
$$
22cdotdfrac{9}{5}=F-32
$$
Isolate the variables on the only side as follows:
$$
F=dfrac{198}{5}+32 F=dfrac{160+198}{5}
$$
$$
F=dfrac{358}{5} F=71.6 text{textdegree}text{F}
$$
The range of temperature in degree of Fahrenheit is $64.4 text{textdegree} Fle xle71.6 text{textdegree} F$
text{color{#c34632}(a) $18 text{textdegree} Cle xle22 text{textdegree} C$
\ \
(b) $64.4 text{textdegree} Fle xle71.6 text{textdegree} F$}
$$
text{color{#4257b2}How long can each volunteer talk to prospective dollars.}
$$
The calls has a billed of $(0.5)$ dollar for the first three minute then billed $(0.1)$ dollar for each minute and the maximum billed per call is not more than $(2)$ dollar.
$because$ First three minute is billed of $(0.5)$ dollar
$therefore$ The price remaining for call is $(2-0.5=1.5)$ dollars
The remaining minute after first three minutes are $=dfrac{1.5}{0.1}=15$ minutes
The minutes needed to talk to prospective dollars are $(15+3=18$ minutes)
text{color{#c34632} $18$ minutes}
$$
text{color{#4257b2}(a) Find a equation that allow conversion from Celsius to Fahrenheit temperature with using question $(12)$}
$$
$$
C=dfrac{5}{9}(F-32)
$$
We need to get the value of $(F)$ in the left side, so follow below steps.
Multiply both of sides by $left(dfrac{9}{5}right)$ as follows:
$$
dfrac{9}{5} C=F-32
$$
Add both of sides by $(32)$ as follows:
$$
F=dfrac{9}{5} C+32 F=1.8C+32
$$
text{color{Brown} $F=1.8C+32$}
$$
For ${color{#4257b2}2x-1<7} 2x<7+1 2x<8$
Divide both of sides by $(2)$ as follows:
$$
x<dfrac{8}{2} x<4
$$
For ${color{#4257b2}-2x+1<7} -2x<7-1 -2x-dfrac{6}{2} x>-3
$$
$$
text{color{#4257b2}(a) Graph the inequality}
$$

text{color{#4257b2}(b) Solve the inequality from the graph }
$$
From the graph, the solution for the inequality is $-3<x<4$
text{color{#c34632} (a) See the graph (b) $-3<x<4$}
$$
text{color{#4257b2}Will the solution to the double inequality is has a upper and lower limit?}
$$
For all double inequality has the upper and lower limit.
Its including but not limited to:
$$
0<x<4, -3<x<2, 1ge xle3
$$
text{color{Brown}$0<x<4, -3<x<2, 1ge xle3$}
$$

*Figure 1.* The graphs of the two functions
Note that red curve is under the blue curve for
$$
-3.94<x<2.76$$
Assume the inequality is $(2<4)$
$$
text{color{#4257b2}(a) Cubing both sides}
$$
$$
(2)^3<(4)^3 8<64
$$
The inequality still true
$$
text{color{#4257b2}(b) Square both sides}
$$
$$
(2)^2<(4)^2 4<16
$$
The inequality still true
$$
text{color{#4257b2}(c) Make both of sides the exponent with base of $(2)$}
$$
$$
(2)^2<(2)^4 4<16
$$
The inequality still true
text{color{#4257b2}(d) Make both of sides the exponent with base of $(0.5)$}
$$
$$
(0.5)^2<(0.5)^4 0.250.0625$
$$
text{color{#4257b2}(e) Taking a reciprocating for both sides }
$$
$$
dfrac{1}{2}dfrac{1}{4}$
$$
text{color{#4257b2}(f) Tacking square root for both sides}
$$
$$
sqrt{2}<sqrt{4} 1.4<2
$$
The inequality still true
text{color{Brown}(a) The inequality still true (b) The inequality still true
\ \
(c) The inequality still true (d) The inequality is not true
\ \
(e) The inequality is not true (f) The inequality still true}
$$
$$
color{#4257b2}text{(a)} x^2<4
$$
Use square root property as follows:
$$
sqrt{x^2}<sqrt{4} x<pm2
$$
$$
x<2 x<-2
$$
color{#4257b2}text{(b)} 4x^2+5ge41
$$
Add both of sides by $(-5)$ as follows:
$$
4x^2ge41-5 4x^2ge36
$$
Divide both of sides by $(4)$ as follows:
$$
x^2ge9
$$
Use square root property as follows:
$$
sqrt{x^2}gesqrt{9} xgepm3
$$
$$
xge3 xge-3
$$

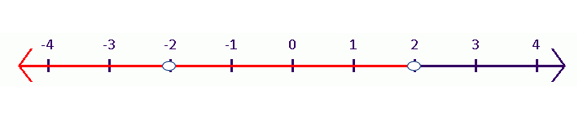
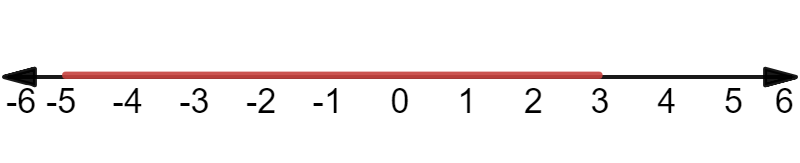
color{#4257b2}text{(c)} |2x+2|<8
$$
For $2x+2<8 2x<8-2 2x<6$
Divide both of sides by $(2)$ as follows:
$$
x<3
$$
For $-2x-2<8 -2x<8+2 -2x-5
$$
$$
-5<x<3
$$
color{#4257b2}text{(d)} -3x^3ge81
$$
Divide both of sides by $(-3)$ as follows:
$$
x^3le-27
$$
Use cubic root property as follows:
$$
sqrt[3]{x^3}le-sqrt[3]{27}
$$
$$
xle-3
$$

text{color{Brown}(a) $x=(-2, 2)$ (b) $x=(-3, 3)$
\ \
(c) $-5<x<3$ (d) $xle-3$}
$$

