What is the domain of $dfrac{2}{5-x}$ ?

To get the domain for the fractional function follow the following steps:

$$
5-xne0
$$

$$
5ne x
$$

The domain for this function is $[x in R| x ne5]$

The correct answer is second one (b)

$$
text{color{Brown}(b) $[x in R| x ne5]$}
$$

The correct selection is third one

$$
color{#4257b2}text{(c)} y=sqrt{x-3}
$$

$$
y=(x-3)^{0.5}
$$

That mean the exponent function has not normal number, so this is another functional.

$$
text{color{Brown}(c) $y=sqrt{x-3}$}
$$

Which function can represent the graph ?

The correct answer is third one (c)

$$
f(x)=|2x-4|
$$

$$
2x-4=0 2x=4
$$

$$
x=dfrac{4}{2} x=2
$$

$$
text{color{Brown}(c) $f(x)=|2x-4|$}
$$

What is the best description for $f(x)=(x-2)(x+2)$?

Use distributive property as follows:

$$
x^2-2x+2x-4
$$

$$
x^2-4
$$

This is a difference completing square, so the degree for equation is even.

The correct answer is second one (b) even

$$
text{color{Brown} (b) even}
$$

What transformation applied to obtain the equation $y=|dfrac{1}{3}(x-2)|$?

The correct answer is forth one (d)

Horizontal translation $(2)$ units to the right and

horizontal compression by a factor of $left(dfrac{1}{3}right)$.

$$
text{color{Brown}Correct answer is (d)}
$$

What is the parent function for the equation $f(x)=dfrac{2}{x-2}-4$

The correct answer is forth one (d)

$$
g(x)=dfrac{1}{x}
$$

$$
text{color{Brown} (d) $g(x)=dfrac{1}{x}$}
$$

Which of the following is the resulting equation?

The correct answer for the question is forth one (d)

$$
f(x)=2^{left(tfrac{1}{5}xright)}-3
$$

According the standard form $f(x)=a(kx-d)+c$

$$
text{color{Brown}(d) $f(x)=2^{left(tfrac{1}{5}xright)}-3$}
$$

Which function has an inverse with the domain $(xin R|xge5)$

The correct selection is second one $y=2(x-5)^2$

When use zero property for the function to get the value of $x$ as folows:

$$
2(x-5)^2=0 (x-5)^2=0
$$

$$
sqrt{x-5)^2}=0 x-5=0 x=5
$$

$$
text{color{Brown}(b) $y=2(x-5)^2$}
$$

Find the inverse function for $f(x)=2x^2-4$?

To find the inverse function follows the next steps:

Isolate the variable $x$ on the left side as follows:

$$
2x^2=y+4
$$

Divide both sides by $2$ as follows:

$$
x^2=dfrac{y+4}{2}
$$

Use square root as follows:

$$
sqrt{x^2}=sqrt{dfrac{y+4}{2}}
$$

$$
x=pmsqrt{dfrac{y+4}{2}}
$$

Substiute the value of $x=y$ as follows:

$$
f(x)=y=pmsqrt{dfrac{x+4}{2}}
$$

The correct answer for the inverse function is third one (c)

$$
text{color{Brown} (c) $f(x)=y=pmsqrt{dfrac{x+4}{2}}$}
$$

$$
text{color{#4257b2}Select which function is not continuous?}
$$

Function to be continuous must be three rules in this function:

$(1) f(a)$ is defined

$(2) limlimits_{xto{a}^-} f(x)=limlimits_{xto{a}^+} f(x)$ $(3) limlimits_{xto a} f(x)=f(x)$

$$
color{#4257b2}(a) f(x)=2x x<1, f(x)=x+1 xge1
$$

$$
f(1)=x+1=1+1 f(1)=2
$$

$$
limlimits_{xto1^-} f(1)=2x=2cdot1 limlimits_{xto1^-} f(1)=2
$$

$$
limlimits_{xto1^+} f(1)=x+1=1+1 limlimits_{xto1^+} f(1)=2
$$

$$
limlimits_{xto1} f(1)=f(1) 2=2
$$

{$text{color{Brown}This function is continuous at $(x=1)$}$

$$
color{#4257b2}(b) f(x)=(x-2)^2 xle2, f(x)=sqrt{x-2} x>2
$$

$$
f(2)=(x-2)^2=(2-2)^2 f(2)=0
$$

$$
limlimits_{xto2^-} f(2)=(x-2)^2=(2-2)^2 limlimits_{xto2^-} f(2)=0
$$

$$
limlimits_{xto2^+} f(2)=sqrt{x-2}=sqrt{2-2} limlimits_{xto2^+} f(2)=0
$$

$$
limlimits_{xto2} f(2)=f(2) 0=0
$$

{$text{color{Brown}This function is continuous at $(x=2)$}$

$$
color{#4257b2}(c) f(x)=dfrac{1}{x} x<-1, f(x)=-1 xge-1
$$

$$
f(-1)=-1
$$

$$
limlimits_{xto-1^-} f(-1)=dfrac{1}{x}=-dfrac{1}{1} limlimits_{xto-1^-} f(-1)=-1
$$

$$
limlimits_{xto-1^+} f(-1)=-1
$$

$$
limlimits_{xto-1} f(-1)=f(-1) -1=-1
$$

{$text{color{Brown}This function is continuous at $(x=-1)$}$

$$
color{#4257b2}(d) f(x)=2x+1 x<2, f(x)=x+2 xge2
$$

$$
f(2)=x+2=2+2 f(2)=4
$$

$$
limlimits_{xto2^-} f(2)=2x+1=2(2)+1 limlimits_{xto2^-} f(2)=5
$$

$$
limlimits_{xto2^+} f(2)=x+2=2+2 limlimits_{xto2^+} f(2)=4
$$

$$
limlimits_{xto2^-} f(2)nelimlimits_{xto2^+} f(2) 4ne5
$$

{$text{color{Brown}This function is not continuous at $(x=2)$
\
$$color{#4257b2}therefore text{The correct answer is forth one}$$}$

$$
text{color{Brown}$$(d) f(x)=2x+1 x<2, f(x)=x+2 xge2$$}
$$

What is the average rate for the function $f(x)=x^3-2x^2+7$

in the interval $-1le xle3$

Find the value of $f(-1)$ as follows:

$$
f(-1)=(-1)^3-2(-1)^2+7
$$

$$
f(-1)=-1-2+7
$$

$$
f(-1)=4
$$

Find the value of $f(3)$ as follows:

$$
f(3)=(3)^3-2(3)^2+7
$$

$$
f(3)=27-18+7
$$

$$
f(3)=16
$$

The average rate of the function is

$$
16-4=12
$$

The correct answer is third one (c) $=12$

$$
text{color{Brown} (c) $=12$}
$$

Whose crystal growth faster?

Kristin rate

Daily rate $=dfrac{5}{3}=1.6$ gm per day.

Husain rate

Daily rate $=dfrac{15}{10}=1.5$ gm per day.

According the daily rate for both, Kristin has grow faster Husain, so

The correct answer is first one (a).

$$
text{color{Brown}(a) Kristin}
$$

$$
text{color{#4257b2}What is the best estimate for the instantaneous change in depth at $(t=3)$?}
$$

By using the values in the the table in the textbook, we use the next point after the point of $9t=3)$ to estimate the instantaneous change in depth as follows:

$$
=dfrac{27.015002-27}{3.001-3}=dfrac{0.015002}{0.001}
$$

Instantaneous change in the depth is equal $15.002$ m/s

The correct answer is second one $(b) 15.002$ m/s

$$
text{color{Brown} $(b) 15.002$ m/s}
$$

What is the best estimate for the rate change for $f(x)=2^x-2x+1$ at $x=1$

Substitute the value of $x=1$ for the equation as follows:

$$
f(x)=2^{-1}-2(-1)+1 f(x)=dfrac{1}{2}+2+1
$$

$$
f(x)=3.5
$$

The correct answer is second one (b)

$$
text{color{Brown}(b) $f(x)=3.5$}
$$

$$
text{color{#4257b2}What is the best estimate of the slope of the tangent at $(x=2)$ for the graph in the textbook}
$$

To get the slope of tangent , you should take any two points on the vertical axis $(y)$ which lies on the graph and the same time on the tangent line, then divided by the faces points on the horizontal axis $(x)$ as follows:

Use points $(2, 8), (3, 5)$

Slope $=dfrac{8-5}{2-3}$ Slope $=dfrac{3}{-1}=-3$

The best slope of the tangent at $(x=2)$ is $(-3)$

The correct answer is forth one $(d)=-3$

$$
text{color{Brown}$(d)=-3$}
$$

$$
text{color{Brown}Figure (c)}
$$

At $x=5$ the function $f(x)=13x-1.3x^2+7.3$

Substitute the value of $x=5$ as follows:

$$
f(x)=13(5)-1.3(5)^2+7.3
$$

$$
f(x)=65-32.5+7.3
$$

$$
f(x)=39.8
$$

This value neither a maximum not a minimum

The correct answer is forth one (d)

$$
text{color{Brown}(d) neither a maximum not a minimum}
$$

Find the correct expression that represent the difference value of quotient

of the interval $3le xle3+b$ for the function $2x^2-3x+9$

Substitute the value of $(x=3, x=3+b)$ as follows:

$$
f(3)=2(3)^2-3(3)+9 18-9+9 f(3)=18
$$

$$
f(3+b)=2(3+b)^2-3(3+b)+9
$$

$$
=2(9+6b+b^2)-3(3+b)+9
$$

$$
f(3+b)=18+12b+2b^2-9-3b+9
$$

Subtract the $f(3+b)-f(3)$ as follows:

$$
18+12b+2b^2-9-3b+9-18
$$

$$
2b^2+9b =b(2b+9)
$$

The factor $(2b+9)$ is a one of the quotient term, so

The correct answer is forth one (d)

$$
text{color{Brown}(d) $(2b+9)$}
$$

What is the maximum value of the equation $y=35(1.7)^x$

if the domain is $0le xle8$

Substitute the value of $x=8$ at maximum value as follows:

$$
y=35(1.7)^8 y=35cdot69.7575
$$

$$
color{#4257b2}y=2441.5
$$

The correct answer is second one (b)

$$
text{color{Brown}(b) $y=2441.5$}
$$

The function does not represent the polynomial function is third one

$$
color{#4257b2}text{(c)} 2^x-3
$$

Because the exponent function has not a normal and natural number, so it is another function.

$$
text{color{Brown} $$text{(c)} 2^x-3$$}
$$

The function which can’t be represented the graph in the textbook is a cubic function

$$
color{#4257b2}text{(b) cubic}
$$

Because the cubic function has a different shape about the graph represent in the textbook.

$$
text{color{Brown}$$text{(b) cubic}$$}
$$

The correct answer is third one

$$
color{#4257b2}text{(c)} xrightarrowpminfty, yrightarrow-infty
$$

(c) $xrightarrowpminfty, yrightarrow-infty$

Find the equation that represent the the graph in text book.

The correct answer is second one due to the following reasons:

(I) The leading coefficient is negative.

(II) the degree of the function is cubic degree$(n=3)$

(III) The graph cross the $x$ axis at ponint $(x=3) (x=0)$

$$
text{color{#4257b2}The correct answer is (a) $-0.1x(x-3)^2$}
$$

$$
text{color{Brown}(a) $-0.1x(x-3)^2$}
$$

Find the quartic function has zeros$[-2, 0, 1, 2, 3]$ and satisfies $f(2)=16$

Substitute the value of $x=2$ to get $f(x)=16$ as follows:

$$
text{(a)} color{#4257b2}f(x)=-2x^4+4x^3+10x^2-12x
$$

$$
16=-2(2)^4+4(2)^3+10(2)^2-12(2)
$$

$$
16=-2(16)+4(8)+10(4)-12(2)
$$

$$
16=-32+32+40-24 16=16
$$

The correct answer is first one

$$
text{(a)} -2x^4+4x^3+10x^2-12x
$$

$$
text{color{Brown}(a) $-2x^4+4x^3+10x^2-12x$}
$$

The correct answer for this question is forth one

(d) $y=(2x-3)^3$

Because the standard form is $y=a(kx-d)^3+c$

$$
text{color{Brown}(d) $y=(2x-3)^3$}
$$

Divided function $(x^3-2x^2+7x+12)$ by $(x^2-3x+4)$

Divided the first term for the two question s as follows:

$$
=dfrac{x^3}{x^2}=x
$$

Then multiply it $(x)$with $(x^2-3x+4)$ as follows:

$$
=x^3-3x^2+4x text{reverse}=-x^3+3x^2-4x
$$

Subtract the reverse result with $(x^3-2x^2+7x+12)$ as follows:

$$
cancel x^3-2x^2+7x+12cancel-x^3+3x^2-4x
$$

$$
x^2+3x+12
$$

Divided the first term for the two question s as follows:

$$
=dfrac{x^2}{x^2}=1
$$

Then multiply it $(1)$with $(x^2-3x+4)$ as follows:

$$
=x^2-3x+4 text{reverse}=-x^2+3x-4
$$

Subtract the reverse result with $(x^2+3x+12)$ as follows:

$$
cancel x^2+3x+12cancel-x^2+3x-4=0
$$

$$
6x+8
$$

$$
(x^3-2x^2+7x+12)=(x+1)(x^2-3x+4)6x+8
$$

The correct answer is third one $6x+8$

$$
text{color{Brown}(c) $6x+8$}
$$

What is the reminder when $(x+3)$ is divided into $(x^4-5x^2+12x+16)$

$f(x)=$ (advisor)(quotient)+reminder

$f(x)=$ (x+3)(quotient)+reminder

Substitute the value of $(x=-3)$ as folloes:

$f(-3)=(-3+3)$(quotient)+reminder

$f(-3)=$ reminder

$$
f(-3)=(-3)^4-5(-3)^2+12(-3)+16
$$

$$
f(-3)=81-45-36+16 f(-3)=16
$$

Reminder $=16$

The correct answer is forth one (d)

$$
text{color{Brown}(d) $16$}
$$

Find the value of $k$ for the equation $2x^3+kx^2-3x+18$ if $(x-3)$ as ne of the factor of the equation.

Substitute the value of $(x=3)$ as follows:

$$
2(3)^3+k(3)^2-3(3)+18=0
$$

$$
(2cdot27)+9k-9+18=0
$$

$$
54+9k+9=0 9k+63=0
$$

$$
9k=-63 k=dfrac{-63}{9} k=-7
$$

The correct answer is second one (b)

$$
text{color{Brown}(b) $k=-7$}
$$

Factor the following equation.

$$
27x^3-216
$$

Use standard form $a^3-b^3=(a-b)(a^2+ab+b^2)$ as follows:

$$
27x^3-216=(3x)^3-6^3
$$

$$
(3x)^3-6^3=(3x-6)(9x^2+18x+36)
$$

Determine the greatest common factor as follows:

$$
3(x-2) 9(x^2+2x+4)
$$

$$
27(x-2)(x^2+2x+4)
$$

The correct answer is third one (c)

$$
text{color{Brown}(c) $27(x-2)(x^2+2x+4)$}
$$

What are the factor of $(x+3)^3+8)$

Use standard form $(a^3+b^3)=(a+b)(a^2-ab+b^2)$ as follows:

$$
=(x+3)^3+8=(x+3)^3+2^3
$$

$$
=(x+3+2)[(x+3)^2-((x+3)cdot2)+4)
$$

$$
=(x+5)((x^2+6x+9)-2x-6+4)
$$

$$
=(x+5)(x^2+4x+7)
$$

The correct answer is third one $(c)$

$$
text{color{Brown} (c) $(x+5)(x^2+4x+7)$}
$$

The graph which represent the relation between the height of water level and the time is graph number $(b)$

Because for the first time the tank need more time to to fill it with water due to the volume of tank in the lower part is larger than the upper part so the height of level water need time more time then growth up normally

$$
text{color{Brown}(b)}
$$

Investigate the transformation of quadratic function and its inverse.

$$
text{color{#4257b2}(a) Sketch the graph of the parent function of $f(x)=x^2)$ and its inverse.}
$$

$$
f(x)=x^2
$$

Graph of the inverse function $f(x)=-x^2$

$text{color{#4257b2}(b) Apply various transformation to the graph of parent function, then draw a graph for inverse function transformed}$.

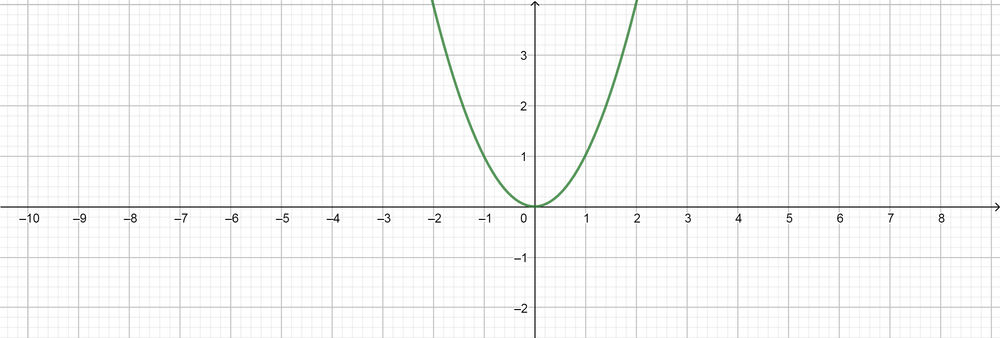
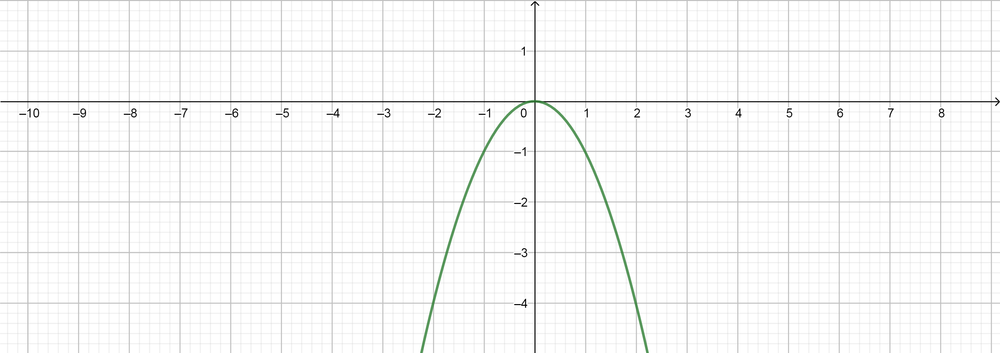
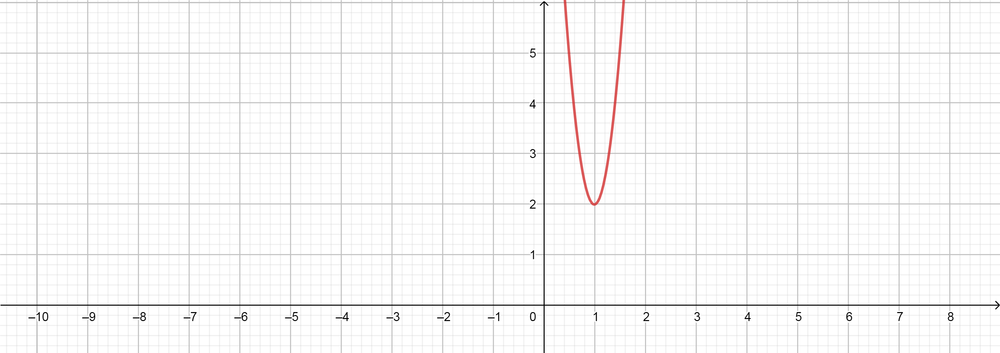
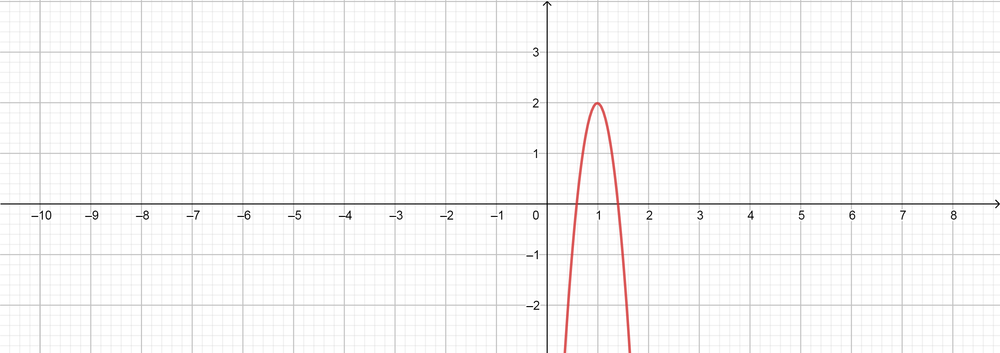
Standard quadratic transformation function is equal, $f(x)=a[k(x-d)]^2+c$

Transformed function for the quadratic function of $f(x)=x^2$ is

$$
f(x)=3[2(x-1)]^2+2
$$

Inverse transformed function is equal $f(x)=-3[2(x-1)]^2+2$

$$
text{color{#4257b2}(c) Describe how you could modify each transformed for the parent function}
$$

Standard transformed function for the quadratic equation is

$$
f(x)=a[k(x-d)]^2+c
$$

** Vertically stretched by a factor of $(3)$

** Horizontal stretched by a factor of $(2)$

** Horizontal translated by $(1)$ unit to the right

** Vertically translated by $(2)$ units up

$$
text{color{#4257b2} For the inverse function}
$$

** Vertical stretched by a factor of $(3)$ and reflected in the $(x)$ axis.

** The same changes are normally.

$$
text{color{Brown}(a) See the graph
\ \
(b) $f(x)=3[2(x-1)]^2+2$ Inverse function is $f(x)=-3[2(x-1)]^2+2$
\ \
(c) Standard transformed function for the quadratic equation is
\ \
$f(x)=a[k(x-d)]^2+c$
\ \
** Vertically stretched by a factor of $(3)$
\ \
** Horizontal stretched by a factor of $(2)$
\ \
** Horizontal translated by $(1)$ unit to the right
\ \
** Vertically translated by $(2)$ units up
\ \
For the inverse function $f(x)=-a[k(x-d)]^2+c$
\ \
** Vertical stretched by a factor of $(3)$ and reflected in the $(x)$ axis.
\ \
** The same changes are normally.}
$$

Investigate various rate of change of the function $[f(x)=x^3-6x^2+9x+1]$, and estimate average rate of change at different points at the graph attached in the textbook.

$$
text{color{#4257b2}From $(x=0)$, to $(x=1)$}
$$

Substitute values of $(x)$ in the cubic function as follows:

$$
f(0)=(0)^3-6(0)^2+9(0)+1 f(0)=0-0+0+1 f(0)=1
$$

$$
f(1)=(1)^3-6(1)^2+9(1)+1 f(1)=1-6+9+1 f(1)=5
$$

Average rate of change is equal, $=dfrac{5-1}{1-0}=dfrac{4}{1}$

Average rate of change is equal, $=4$

$$
text{color{#4257b2}From $(x=1)$, to $(x=2)$}
$$

Substitute values of $(x)$ in the cubic function as follows:

$$
f(1)=(1)^3-6(1)^2+9(1)+1 f(1)=1-6+9+1 f(1)=5
$$

$$
f(2)=(2)^3-6(2)^2+9(2)+1 f(2)=8-24+18+1 f(2)=3
$$

Average rate of change is equal, $=dfrac{3-5}{2-1}=-dfrac{2}{1}$

Average rate of change is equal, $=-2$

$$
text{color{#4257b2}From $(x=2)$, to $(x=3)$}
$$

Substitute values of $(x)$ in the cubic function as follows:

$$
f(2)=(2)^3-6(2)^2+9(2)+1 f(2)=8-24+18+1 f(2)=3
$$

$$
f(3)=(3)^3-6(3)^2+9(3)+1 f(3)=27-54+27+1 f(3)=1
$$

Average rate of change is equal, $=dfrac{1-3}{3-2}=-dfrac{2}{1}$

Average rate of change is equal, $=-2$

$$
text{color{#4257b2}From $(x=3)$, to $(x=4)$}
$$

Substitute values of $(x)$ in the cubic function as follows:

$$
f(3)=(3)^3-6(3)^2+9(3)+1 f(3)=27-54+27+1 f(3)=1
$$

$$
f(4)=(4)^3-6(4)^2+9(4)+1 f(4)=64-96+36+1 f(4)=5
$$

Average rate of change is equal, $=dfrac{5-1}{4-3}=dfrac{4}{1}$

Average rate of change is equal, $=4$

$$
text{color{Brown} From $(x=0)$ to $(x=1)$ Average rate is $=4$
\ \
From $(x=1)$ to $(x=2)$ Average rate is $=-2$
\ \
From $(x=2)$ to $(x=3)$ Average rate is $=-2$
\ \
From $(x=3)$ to $(x=4)$ Average rate is $=4$}
$$

Answer for the following questions.

$text{color{#4257b2}(a) Determine the equation $f(x)=k(x+1)^2(x-2)(x-4)$ if $(1, -24)$ is a point in the graph}$.

Substitution the point $(1, -24)$ to get the value of $k$ as follows:

$$
-24=k(1+1)^2(1-2)(1-4) -24=k(1cdot-1cdot-3)
$$

$$
-24=kcdot3 k=dfrac{-24}{3} k=-8
$$

$$
f(x)=-8(x+1)^2(x-2)(x-4)
$$

$text{color{#4257b2}(b) Solve for $p$ if $(3, p)$ point on the graph}$.

Substitution the point $(3, p)$ as follows:

$$
p=-8(3+1)^2(3-2)(3-4) p=8(16cdot1cdot-1)
$$

$$
p=8cdot-16 p=128
$$

$text{color{#4257b2}(c) State the end behavior and zeros for $f(x)$}$.

$$
f(x)=-8(x+1)^2(x-2)(x-4)
$$

Zeros are $[x=pm1 x=2 x=4]$

The degree of the function is quartic $[n=4]$, so the end behavior is the same due to the degree is even.

$text{color{#4257b2}(d) Determine the $y$ intercept for $f(x)$}$.

Substitute the value of $x=0$ as follows:

$$
f(x)=-8(x+1)^2(x-2)(x-4) f(x)=-8(1cdot-2cdot-4)
$$

$$
f(x)=-8cdot8 f(x)=-64
$$

{$text{color{#4257b2}(e) The possible graph of $f(x)$}$

$$
text{color{Brown}(a) $f(x)=-8(x+1)^2(x-2)(x-4)$
\ \
(b) $p=128$
\ \
(c) Zeros are $[x=pm1 x=2 x=4]$
\ \
The end behavior is the same due to the degree is even.
\ \
(d) $f(x)=-64$}
$$