Answer for the following questions.

(a) Write the standard equation of the polynomial function, then state the degree and leading coefficient.

Standard form is $y= ax+b$

For cubic function is $(y=ax^3+bx^2+cx+d)$ as follows:

$$
y=6x^3+x^2-12x+5
$$

Degree is $(n=3)$ Leading coefficient is $(6)$

(b) Write the greatest number of turning point that equation have.

This equation may have $(2)$ and $(0)$ turning points, so

the greatest one is $(2)$

(c) Write the greatest number of zeros that equation have.

This equation may have $(1, 2, 3)$ zeros, so

the greatest one is $(3)$

(d) If the least number of zeros is $(1)$ write the degree of the function.

The degree of the function that have least number of zeros is $(1)$ is cubic function $(n=3)$

$$
text{color{Brown}a) $y=ax^3+bx^2+cx+d$ $y=6x^3+x^2-12x+5$
\ \
b) greatest one is $(2)$. c) greatest one is $(3)$. d) cubic function $(n=3).$}
$$

Determine the equation of polynomial function of the graph shown on the text book.

$$
text{color{#4257b2}From the graph:}
$$

This is a cubic function and zeros are:

$$
[x=-4 x=-2 x=2]
$$

The equation is $f(x)=(x+4)(x+2)(x-2)$

$$
f(x)=(x+4)(x^2-4)
$$

$$
text{color{Brown} $f(x)=(x+4)(x^2-4)$}
$$

Factor the following expression.

$$
color{#4257b2}text{(a)} 2x^3-x^2-145x-72
$$

Use greatest common factor as follows :

$$
x^2(2x-1)-72(2x-1)
$$

$$
(2x-1)(x^2-72)
$$

$$
color{#4257b2}text{(b)} (x-7)^3+(2x+3)^3
$$

According standard form $a^3+b^3=(a+b)(a^2-ab+b^2)$

$$
begin{align*}
(x-7)^3+(2x+3)^3 &=(x-7+2x+3)[(x-7)^2-((x-7)(2x+3))+(2x+3)^2]
\ \
&=(3x-4)[(x^2-14x+49)-(2x^2-11x-21)+(4x^2+12x+9)]
\ \
&=(3x-4)(x^2-14x+49-2x^2+11x+21+4x^2+12x+9)
end{align*}
$$

Rearrange the tiles to group like terms as follows:

$$
=(3x-4)[(x^2-2x^2+4x^2)+(-14x+11x+12x)+(49+21+9)]
$$

$$
=(3x-4)(3x^2+9x+79)
$$

$$
text{color{Brown}(a) $(2x-1)(x^2-72)$
\ \
(b) $(3x-4)(3x^2+9x+79)$}
$$

The original function is $f(x)=x^3-4x^2$ then translated into one unit up so,

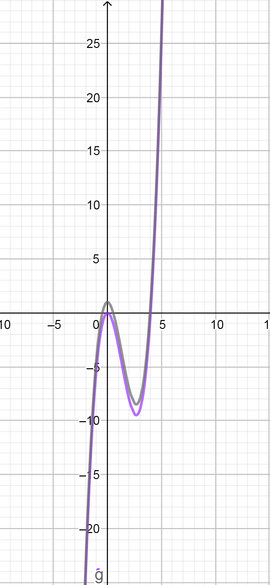
The new function is $f(x)=x^3-4x^2+1$

According the graph has number of zeros more than the original function.

Zeros of the original function are $(x=0, x=4)$

Zeros of the new function are $(x=-0.5, x=0.5, x=4)$

$$
text{color{Brown}The graph has number of zeros more than the original function.}
$$

During which interval of $(x)$ the graph of function

$f(x)=-(x+3)(x+5)(x-1)$ below the $(x)$ axis.

From the graph the interval is $(-5le xle1)$

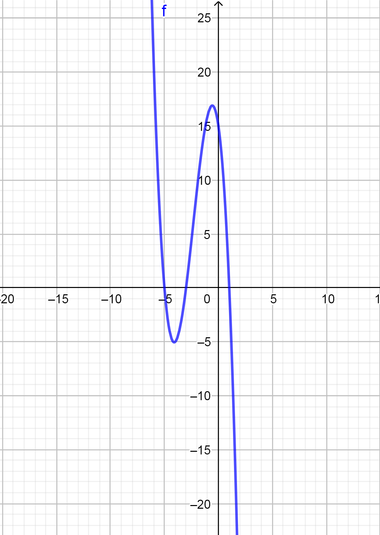
$$
text{color{Brown} $(-5le xle1)$}
$$

Divided function $(6x^3+x^2-12x+5)$ by $(2x-1)$

Divided the first term for the two question s as follows:

$$
=dfrac{6x^3}{2x}=3x^2
$$

Then multiply it $(3x^2)$with $(2x-1)$ as follows:

$$
(3x^2)(2x-1)=6x^3-3x^2 text{reverse}=-6x^3+3x^2
$$

Subtract the reverse result with $(6x^3+x^2-12x+5)$ as follows:

$$
cancel 6x^3+x^2-12x+5cancel-6x^3+3x^2
$$

$$
4x^2-12x+5
$$

Divided the first term for the two question s as follows:

$$
=dfrac{4x^2}{2x}=2x
$$

Then multiply it $(2x)$with $(2x-1)$ as follows:

$$
=4x^2-2x text{reverse}=-4x^2+2x
$$

Subtract the reverse result with $(4x^2-12x+5)$ as follows:

$$
cancel4x^2-12x+5cancel-4x^2+2x=0
$$

$$
-10x+5
$$

Divided the first term for the two question s as follows:

$$
=dfrac{-10x}{2x}=-5
$$

Then multiply it $(-5)$with $(2x-1)$ as follows:

$$
=-10x+5 text{reverse}=10x-5
$$

Subtract the reverse result with $(-10x+5)$ as follows:

$$
cancel-10xcancel+5+cancel10xcancel-5=0
$$

$$
(6x^3+x^2-12x+5)=(2x-1)(3x^2+2x-5)
$$

The term $(2x-1)$ is the factor of the dividend

$$
text{color{Brown}$$(6x^3+x^2-12x+5)=(2x-1)(3x^2+2x-5)$$}
$$

Answer for the following question.

$$
text{color{#4257b2}(a) Write the equation for transformed function.}
$$

Note that: $a=5 k=dfrac{1}{2} d=2 c=4$

Use standard form $y=a[k(x-d)]+c$

Parent function is $y=x^3$

$$
y=5left[dfrac{1}{2}(x-2)right]^3+4
$$

$$
text{color{#4257b2}(b) Determine the new points on the transformed function if $(1, 1)$ is a point on the parent function.}
$$

Substitute the value of $(x=1)$ on the transformed function to get the value of $(y)$ as follows:

$$
y=5left[dfrac{1}{2}(x-2)right]^3+4
$$

$$
y=5left[dfrac{1}{2}(1-2)right]^3+4
$$

$$
y=5left[dfrac{1}{2}(-1)right]^3+4
$$

$$
y=5left[-dfrac{1}{2}right]^3+4
$$

$$
y=5left[-dfrac{1}{8}right]+4
$$

$$
y=-dfrac{5}{8}+4 y=dfrac{-5+32}{8}
$$

$$
y=dfrac{27}{8} y=3.375
$$

The new point on the transformed function is $(1, 3.375)$

$$
text{color{Brown}(a) $y=5left[dfrac{1}{2}(x-2)right]^3+4$ (b) $(1, 3.375)$}
$$

Find the polynomial which Julie divided by it?

The equation is $x^4+3x^3-9x^2+6$

The answer was $x^3-2x^2+x-5$ and the reminder was $31$

$$
text{color{#4257b2}Note that:}
$$

$f(x)=$ divisor $cdot$ quotient + reminder

$x^4+3x^3-9x^2+6=$ advisor $(x^3-2x^2+x-5) +31$

$x^4+3x^3-9x^2+6-31=$ advisor $(x^3-2x^2+x-5)$

$x^4+3x^3-9x^2-25=$ advisor $(x^3-2x^2+x-5)$

Divisor$=x^4+3x^3-9x^2-25div x^3-2x^2+x-5$

Using the divided method to get the divided as follows:

Divided the first term for the two question s as follows:

$$
=dfrac{x^4}{x^3}=x
$$

Then multiply it $(x)$with $(x^3-2x^2+x-5)$ as follows:

$$
=x^4-2x^3+x^2-5x
$$

Subtract the result with $(x^4+3x^3-9x^2-25)$ as follows:

$$
cancel{-x^4}+2x^3-x^2+5xcancel{x^4}+3x^3-9x^2-25
$$

$$
5x^3-10x^2+5x-25
$$

Divided the first term for the two question s as follows:

$$
=dfrac{5x^3}{x^3}=5
$$

Then multiply it $(5)$with $(x^3-2x^2+x-5)$ as follows:

$$
=5x^3-10x^2+5x-25
$$

Subtract the result with $(5x^3-10x^2+5x-25)$ as follows:

$$
5x^3-10x^2+5x-25-5x^3+10x^2-5x+25=0
$$

Julie divided by $x+5$

$$
text{color{Brown} Large $(x+5)$}
$$

Determine the value of $a$ and then located the other zeros and sketch the function $f(x)=ax^4+8x^2$

Note that the one of zeros $(x=2)$ and absolute maximum $(8)$

Substitute the values of $(x=2, y=8)$ as follows:

$$
8=a(2)^4+8(2)^2 8=16a+32
$$

$$
16a=8-32 16a=-24
$$

Divide both of sides by $(16)$ as follows:

$$
a=dfrac{-24}{16} a=-1.5
$$

$$
color{#4257b2} -1.5x^4+8x^2
$$

Determine the greatest common factor as follows:

$$
-x^2 (1.5x^2-8)
$$

Use zero property as follows:

$$
-x^2=0 x^2=0 x=0
$$

$$
1.5x^2-8=0 1.5x^2=8
$$

Divide both of sides by $(1.5)$ as follows:

$$
x^2=dfrac{8}{1.5} x^2=5.33
$$

Use square root property as follows:

$$
sqrt{x^2}=sqrt{5.33} x=pm 2.309
$$

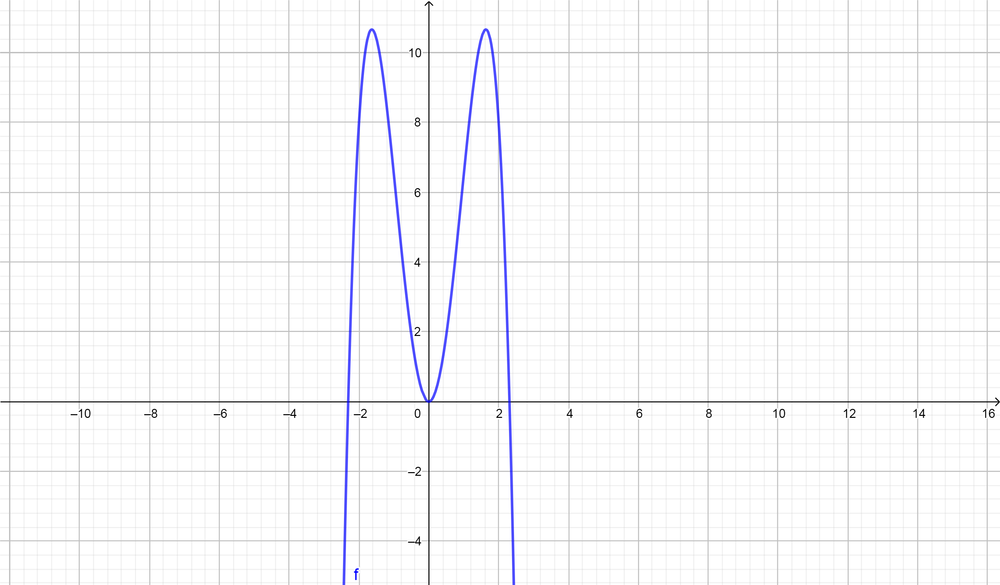
$$
text{color{Brown}$a=-1.5$
\ \
Zeros are $[0, 2, 2.309, -2.039]$}
$$