Match the following expression with matched figure in text book.

$$
color{#4257b2}text{(a)} y=2(x-3)^3+1
$$

The leading coefficient is positive, so the equation is upward and degree is $(3)$, cubic function

$$
text{Figure} (B)
$$

$$
color{#4257b2}text{(b)} y=-dfrac{1}{3}(x+1)^3-1
$$

The leading coefficient is negative, so the equation is downward and degree is $(3)$, cubic function

$$
text{Figure} (C)
$$

$$
color{#4257b2}text{(C)} y=0.2(x-4)^4-3
$$

The leading coefficient is positive, so the equation is upward and degree is $(4)$, quartic function

$$
text{Figure} (A)
$$

$$
color{#4257b2}text{(D)} y=-1.5(x+3)^4+4
$$

The leading coefficient is negative, so the equation is downward and degree is $(4)$, quartic function

$$
text{Figure} (D)
$$

$$
text{color{Brown}(a) $text{Figure} (B)$ (b) $text{Figure} (C)$
\ \
(c) $text{Figure} (A)$ (d) $text{Figure} (D)$}
$$

$$
color{#4257b2}text{(a)} y=dfrac{5}{4} x^4+3
$$

Parent function is $y=x^4$

Vertical compression by $dfrac{5}{4}$

Vertical translation by $3$ units up

$$
color{#4257b2}text{(b)} y=3x-1
$$

Parent function is $y=x$

Vertical compression by $3$

Vertical translation by $1$ down

$$
color{#4257b2}text{(c)} y=(3x+4)^3-7
$$

Parent function is $y=x^3$

Vertical compression by $3$

Horizontal translation by $4$ units left

Vertical translation by $7$ down

$$
color{#4257b2}text{(d)} y=-(x+8)^4
$$

Parent function is $y=x^4$

Vertical compression by $a=-1$

Horizontal translation by $8$ units left

$$
color{#4257b2}text{(e)} y=-4.8(x-3)(x-3)
$$

$$
y=-4.8(x-3)^2
$$

Parent function is $y=x^2$

Vertical compression by $a=-4.8$

Horizontal translation by $3$ units right

$$
color{#4257b2}text{(f)} y=2[dfrac{1}{2} x+7]^3-4
$$

Parent function is $y=x^3$

Vertical compression by $a=2$

Horizontal translation by $7$ units left

Vertical translation by $4$ units down

$$
text{color{Brown}(a) $y=x^4 a=dfrac{5}{4} c=-3$
\ \
(b) $y=x a=3 c=-1$
\ \
(c) $y=x^3 a=3 d=-4 c=-7$
\ \
(d) $y=x^4 a=-1 d=-8$
\ \
(e) $y=x^2 a=-4.8 c=3$
\ \
(f) $y=x^3 a=2 d=-7 c=-4$}
$$

$$
text{color{#4257b2}(a) Describe the transformation that are applied to the attached graph in the textbook for the parent function of $f(x)=x^3$}
$$

The center point of the parent function $f(x)=x^3$ is equal $(0, 0)$, and the center point of transformed function is equal $(-3, -4)$, so the function transformed by the following terms:

** Vertically translated by $(4)$ units down on the $(y)$ axis.

** Horizontal translated by $(3)$ units to the left side on the $(x)$ axis.

$$
f(x)=(x+3)^3-4
$$

$$
text{color{#4257b2}(b) Describe the transformation that are applied to the attached graph in the textbook for the parent function of $f(x)=x^4$}
$$

The center point of the parent function $f(x)=x^4$ is equal $(0, 0)$, and the center point of transformed function is equal $(-4, 5)$, so the function transformed by the following terms:

** Vertically translated by $(5)$ units up on the $(y)$ axis.

** Horizontal translated by $(4)$ units to the left side on the $(x)$ axis.

** Horizontal compressed by $(1.2)$ and reflected to the $(x)$ axis

$$
f(x)=-[1.2 (x+4)]^4+5
$$

$$
text{color{#4257b2}(c) Describe the transformation that are applied to the attached graph in the textbook for the parent function of $f(x)=x^4$}
$$

The center point of the parent function $f(x)=x^4$ is equal $(0, 0)$, and the center point of transformed function is equal $(1, -2)$, so the function transformed by the following terms:

** Vertically translated by $(2)$ units down on the $(y)$ axis.

** Horizontal translated by $(1)$ units to the right side on the $(x)$ axis.

** Horizontal stretched by factor of $(0.7)$ .

$$
f(x)=[0.7 (x-1)]^4-2
$$

$$
text{color{#4257b2}(d) Describe the transformation that are applied to the attached graph in the textbook for the parent function of $f(x)=x^3$}
$$

The center point of the parent function $f(x)=x^3$ is equal $(0, 0)$, and the center point of transformed function is equal $(3, -4)$, so the function transformed by the following terms:

** Vertically translated by $(4)$ units down on the $(y)$ axis.

** Horizontal translated by $(3)$ units to the right side on the $(x)$ axis.

** Vertically stretched by factor of $(2)$ and reflected to the $(x)$ axis.

$$
f(x)=-2(x-3)^3-4
$$

$$
text{color{Brown}(a) $f(x)=(x+3)^3-4$ (b) $f(x)=-[1.2 (x+4)]^4+5$
\ \
(c) $f(x)=[0.7 (x-1)]^4-2$ (d) $f(x)=-2(x-3)^3-4$}
$$

Describe the transformation for the following expression.

$$
color{#4257b2}text{(a)} y=12(x-9)-7
$$

Vertical compression $a=12$

Horizontal translation $9$ units right

Vertical translation $7$ units down

$$
color{#4257b2}text{(b)} y=(x+9)(x+9)(x+9)
$$

$$
y=(x+9)^3
$$

Vertical compression $a=1$

Horizontal translation $9$ units left

$$
color{#4257b2}text{(c)} y=[dfrac{7}{8}(x+1)]^3+3
$$

$$
k=dfrac{7}{8}
$$

Horizontal translation $1$ units left

Vertical translation $3$ units up

$$
color{#4257b2}text{(d)} y=-2[-3(x-4)]^3-5
$$

$$
k=-3
$$

Vertical compression $a=-2$

Horizontal translation $4$ units right

Vertical translation $5$ units down

$$
color{#4257b2}text{(e)} y=-2(x-6)^3-8
$$

Vertical compression $a=-2$

Horizontal translation $6$ units right

Vertical translation $8$ units down

$$
color{#4257b2}text{(f)} y=[dfrac{3}{4}(x-10)]^3
$$

$$
k=dfrac{3}{4}
$$

Horizontal translation $10$ units right

$$
text{color{Brown}(a) $a=12 d=9 c=-7$
\ \
(b) $a=1 d=9$
\ \
(c) $k=dfrac{7}{8} d=-1 c=3$
\ \
(d) $a=-2 k=-3 d=4 c=-5$
\ \
(e) $a=-2 d=6 c=-8$
\ \
(f) $k=dfrac{3}{4} d=10$}
$$

$$
text{color{#4257b2}(a) Describe the transformation that are applied to the attached graph in the textbook for the parent function of $f(x)=x^2$}
$$

The center point of the parent function $f(x)=x^2$ is equal $(0, 0)$, and the center point of transformed function is equal $(0, 1.25)$, so the function transformed by the following terms:

** Vertically translated by $(1.25)$ units up on the $(y)$ axis.

** Horizontal stretched by factor of $(0.5)$ and reflected to the $(x)$ axis.

$$
f(x)=-left(dfrac{1}{2} xright)^2+1.25
$$

$$
text{color{#4257b2}(b) Describe the transformation that are applied to the attached graph in the textbook for the parent function of $f(x)=x^2$}
$$

The center point of the parent function $f(x)=x^2$ is equal $(0, 0)$, and the center point of transformed function is equal $(0, -11)$, so the function transformed by the following terms:

** Vertically translated by $(11)$ units down on the $(y)$ axis.

** Horizontal compressed by factor of $(2.8)$.

$$
f(x)=(2.8x)^2-11
$$

$text{$text{color{Brown}(a) $f(x)=-left(dfrac{1}{2} xright)^2+1.25$ (b) $f(x)=(2.8 x)^2-11$
\ \}$}$

$$
text{color{#c34632}If $y=x^3$ and passes through the points of $(-1, -1), (0, 0), (2, 8)$. List the coordinates of these transformed points for the following transformed terms.}
$$

$$
color{#4257b2}(a) a=dfrac{1}{2} k=dfrac{1}{5} d=-6
$$

Multiply coordinates of points $(x)$ by $left(dfrac{1}{5}right)$ and coordinates of points $(y)$ by $left(dfrac{1}{2}right)$, $(x, y) rightarrowleft(dfrac{1}{5} x, dfrac{1}{2} yright)$, as follows:

$$
(-1, -1) rightarrow left(-dfrac{1}{5}, -dfrac{1}{2}right)
$$

$$
(0, 0) rightarrow (0, 0)
$$

$$
(2, 8) rightarrow left(dfrac{2}{5}, 4right)
$$

Add to the coordinates of points $(x)$ by $(-6)$, $left(dfrac{1}{5} x, dfrac{1}{2} yright) rightarrow left(dfrac{1}{5} x-6, dfrac{1}{2} yright)$, as follows:

$$
left(-dfrac{1}{5}, -dfrac{1}{2}right) rightarrow left(-dfrac{31}{5}, -dfrac{1}{2}right)
$$

$$
(0, 0) rightarrow (-6, 0)
$$

$$
left(dfrac{2}{5}, 4right) rightarrow left(-dfrac{28}{5}, 4right)
$$

$$
color{#4257b2}(b) k=dfrac{1}{2} c=3
$$

Multiply coordinates of points $(x)$ by $left(dfrac{1}{2}right)$, $(x, y) rightarrowleft(dfrac{1}{2} x, yright)$, as follows:

$$
(-1, -1) rightarrow left(-dfrac{1}{2}, -1right)
$$

$$
(0, 0) rightarrow (0, 0)
$$

$$
(2, 8) rightarrow (1, 8)
$$

Add to the coordinates of points $(y)$ by $(3)$, $left(dfrac{1}{2} x, yright) rightarrow left(dfrac{1}{2} x, y+3right)$, as follows:

$$
left(-dfrac{1}{2}, -1right) rightarrow left(-dfrac{1}{2}, 2right)
$$

$$
(0, 0) rightarrow (0, 3)
$$

$$
(1, 8) rightarrow (1, 11)
$$

$$
color{#4257b2}(c) a=-3 d=4 c=-dfrac{1}{2}
$$

Multiply coordinates of points $(y)$ by $(-3))$, $(x, y) rightarrow (x, -3y)$, as follows:

$$
(-1, -1) rightarrow (-1, 3)
$$

$$
(0, 0) rightarrow (0, 0)
$$

$$
(2, 8) rightarrow (2, -24)
$$

Add to the coordinates of points $(x)$ by $(4)$, and coordinates of points $(y)$ by $left(-dfrac{1}{2}right)$, $(x, -3y) rightarrow left(x+4, y-dfrac{1}{2}right)$, as follows:

$$
(-1, 3) rightarrow left(3, dfrac{5}{2}right)
$$

$$
(0, 0) rightarrow left(4, -dfrac{1}{2}right)
$$

$$
(2, -24) rightarrow left(6, -dfrac{49}{2}right)
$$

$$
color{#4257b2}(d) a=dfrac{1}{10} k=7 c=-2
$$

Multiply coordinates of points $(x)$ by $(7)$ and coordinates of points $(y)$ by $left(dfrac{1}{10}right)$, $(x, y) rightarrowleft(7 x, dfrac{1}{10} yright)$, as follows:

$$
(-1, -1) rightarrow left(-7, -dfrac{1}{10}right)
$$

$$
(0, 0) rightarrow (0, 0)
$$

$$
(2, 8) rightarrow left(14, dfrac{4}{5}right)
$$

Add to the coordinates of points $(y)$ by $(-2)$, $left(7 x, dfrac{1}{10} yright) rightarrow left(7 x, dfrac{1}{10} y-2right)$, as follows:

$$
left(-7, -dfrac{1}{10}right) rightarrow left(-7, -dfrac{21}{10}right)
$$

$$
(0, 0) rightarrow (0, -2)
$$

$$
left(14, dfrac{4}{5}right) rightarrow left(14, -dfrac{6}{5}right)
$$

$$
color{#4257b2}(e) a=-1 k=-1 c=dfrac{9}{10}
$$

Multiply coordinates of points $(x)$ by $(-1)$ and coordinates of points $(y)$ by $(-1)$, $(x, y) rightarrow (-x, -y)$, as follows:

$$
(-1, -1) rightarrow (1, 1)
$$

$$
(0, 0) rightarrow (0, 0)
$$

$$
(2, 8) rightarrow (-2, -8)
$$

Add to the coordinates of points $(y)$ by $left(dfrac{9}{10}right)$, $(-x, -y) rightarrow left(-x, -y+dfrac{9}{10}right)$, as follows:

$$
(1, 1) rightarrow left(1, dfrac{19}{10}right)
$$

$$
(0, 0) rightarrow left(0, dfrac{9}{10}right)
$$

$$
(-2, -8) rightarrow left(-2, -dfrac{71}{10}right)
$$

$$
color{#4257b2}(a) k=7 d=-4 c=-2
$$

Multiply coordinates of points $(x)$ by $(7)$, $(x, y) rightarrow (7 x, y)$, as follows:

$$
(-1, -1) rightarrow (-7, -1)
$$

$$
(0, 0) rightarrow (0, 0)
$$

$$
(2, 8) rightarrow (14, 8)
$$

Add to the coordinates of points $(x)$ by $(-4)$, and coordinates of points $(y)$ by $(-2)$ $(7 x, y) rightarrow (7x-4, y-2)$, as follows:

$$
(-7, -1) rightarrow (-11, -3)
$$

$$
(0, 0) rightarrow (-4, -2)
$$

$$
(14, 8) rightarrow (10, 6)
$$

$$
text{color{Brown}(a) $left(-dfrac{31}{5}, -dfrac{1}{2}right) (-6, 0) left(-dfrac{28}{5}, -4right)$
\ \ \
(b) $left(-dfrac{1}{2}, 2right) (0, 3) (1, 11)$
\ \ \
(c) $left(3, dfrac{5}{2}right) left(4, -dfrac{1}{2}right) left(6, -dfrac{49}{2}right)$
\ \ \
(d) $left(-7, -dfrac{21}{10}right) (0, -2) left(14, -dfrac{6}{5}right)$
\ \ \
(e) $left(1, dfrac{19}{10}right) left(0, dfrac{9}{10}right) left(-2, -dfrac{71}{10}right)$
\ \ \
(f) $(-11, -3) (-4, -2) (10, 6)$}
$$

$$
text{color{#4257b2}Describe the transformation that are applied to the attached graph in the textbook for the parent function of $f(x)=x^4$}
$$

The center point of the parent function $f(x)=x^4$ is equal $(0, 0)$, and the center point of transformed function is equal $(1, 13)$, so the function transformed by the following terms:

** Vertically translated by $(13)$ units up on the $(y)$ axis.

** Horizontal translated by $(1)$ units to the right side on the $(x)$ axis.

** Horizontal stretched by factor of $(0.73)$ and reflected to the $(x)$ axis.

$$
f(x)=-[0.73(x-1)]^4+13
$$

$$
text{color{Brown}$$f(x)=-[0.73(x-1)]^4+13$$}
$$

The function of $g(x)=x^3$ has transformed by the following terms:

$$
color{#4257b2}a=-dfrac{3}{2} d=13 c=-13
$$

Three points on resulting curve are:

$$
left(11, -dfrac{23}{2}right) (13, -13) left(15, -dfrac{55}{3}right)
$$

$$
text{color{#4257b2}Find the original points of coordinates of these three points of $g(x)$}
$$

Use transformed value to get the original coordinates as follows:

Add to the coordinates of points $(x)$ by $(-13)$, coordinates of points $(x)$ by $(13)$ $(x, y) rightarrow (x-13, y+13)$, as follows:

$$
left(11, -dfrac{23}{2}right) rightarrow left(-2, dfrac{3}{2}right)
$$

$$
(13, -13) rightarrow (0, 0)
$$

$$
left(15, -dfrac{55}{3}right) rightarrow left(2, -dfrac{16}{3}right)
$$

Multiply coordinates of points $(y)$ by $left(dfrac{2}{3}right)$, $(x-13, y+13) rightarrowleft(x-13, dfrac{2}{3} (y+13)right)$, as follows:

$$
left(-2, dfrac{3}{2}right) rightarrow (-2, 1)
$$

$$
(0, 0) rightarrow (0, 0)
$$

$$
left(2, -dfrac{16}{3}right) rightarrow (2, 8)
$$

The original points are,

$$
(-2, 1) (0, 0) (2, 8)
$$

$$
text{color{Brown}$$(-2, 1) (0, 0) (2, 8)$$}
$$

Determine the $x$ intercepts for the following expressions.

$$
color{#4257b2}text{(a)} y=2(x+3)^4-2
$$

Substitute the $y=0$ as follows:

$$
2(x+3)^4-2=0 2(x+3)^4=2
$$

Divide the both sides by $2$ as foloows:

$$
(x+3)^4=dfrac{2}{2} (x+3)^4=1
$$

$$
sqrt[4]{(x+3)^4}=sqrt[4]{1} x+3=1
$$

$$
x=1-3 x=-2
$$

$$
color{#4257b2}text{(b)} y=(x-2)^3-8
$$

Substitute the $y=0$ as follows:

$$
(x-2)^3-8=0 (x-2)^3=8
$$

Use cubic root as follows:

$$
sqrt[3]{(x-2)^3}=sqrt[3]{8} x-2=2
$$

$$
x=2+2 x=4
$$

$$
color{#4257b2}text{(c)} y=-3(x+1)^4+48
$$

Substitute the $y=0$ as follows:

$$
-3(x+1)^4+48=0 -3(x+1)^4=-48
$$

Divide the both sides by $-3$ as foloows:

$$
(x+1)^4=dfrac{-48}{-3} (x+1)^4=16
$$

$$
sqrt[4]{(x+1)^4}=sqrt[4]{16} x+1=2
$$

$$
x=2-1 x=1
$$

$$
color{#4257b2}text{(d)} y=-5(x+6)^4-10
$$

Substitute the $y=0$ as follows:

$$
-5(x+6)^4-10=0 -5(x+6)^4=10
$$

Divide the both sides by $-5$ as foloows:

$$
(x+6)^4=dfrac{10}{-5} (x+6)^4=-2
$$

$$
sqrt[4]{(x+6)^4}=sqrt[4]{-2}
$$

No solution

$$
color{#4257b2}text{(e)} y=4(x-8)^4-12
$$

Substitute the $y=0$ as follows:

$$
4(x-8)^4-12=0 4(x-8)^4=12
$$

Divide the both sides by $4$ as foloows:

$$
(x-8)^4=dfrac{12}{4} (x-8)^4=3
$$

$$
sqrt[4]{(x-8)^4}=sqrt[4]{3}
$$

$$
x-8=sqrt[4]{3} x=sqrt[4]{3}+8
$$

$$
color{#4257b2}text{(f)} y=-(2x+5)^3-20
$$

Substitute the $y=0$ as follows:

$$
-(2x+5)^3-20=0 -(2x+5)^3=20
$$

Multiply the both sides by $-1$ as foloows:

$$
(2x+5)^3=-20
$$

$$
sqrt[3]{(x+5)^3}=sqrt[3]{-20}
$$

No solution

$$
text{color{Brown}(a) $x=-2$ (b) $x=4$
\ \
(c) $x=1$ (d) No solution.
\ \
(e) $sqrt[4]{3}+8$ (f) No solution.}
$$

Answer for the following question if you have a function $y=2(x-4)^n+1$

$$
text{color{#4257b2}(a) How many zeros the function will have at $n=3$?}
$$

If the degree of the function $(n=3)$, so the function may have $[1, 2, 3]$

$$
text{color{#4257b2}(b) How many zeros the function will have at $n=4$?}
$$

If the degree of the function $(n=4)$, so the function may have $[0, 1, 2, 3, 4]$

$$
text{color{#4257b2}(c) State a general rule about the number of zeros for any values of $n$}
$$

Polynomial function of degree $n$ may have up to $n$ distinct zeros

A polynomial function for odd degree must have at least one zeros.

A polynomial function for even degree may have no zeros.

$$
text{color{Brown}(a) $n=3 [1,2,3]$
\ \
(b) $n=4 [0, 1, 2, 3]$
\ \
(c) Polynomial function of degree $n$ may have up to $n$ distinct zeros}
$$

Note that reflection of the function $y=x^n$ we can interpret as
$$
y=(-x)^n,
$$
where the minus sign is affected by the exponent, while the reflection in $y$ axis as
$$
y=-(x)^n,
$$
where the minus sign is not affected by the exponent.

*(a)* If we need the reflection in the $x$ axis and $y$ axis to be equal, we need to find $n$ for which
$$
(-x)^n=-x^n.$$
We can obtain this for odd values of $n$ because odd exponents preserve the sign of the base variable.

*(b)* If we need the reflection in the $x$ axis and $y$ axis to be different, we need to find $n$ for which
$$
(-x)^n not= -x^n.$$
We can obtain this for even values of $n$ because even exponents give an absolute value of the base variable, hence we have that reflection in $x$ gives $x^n$, while reflection in $y$ gives $-x^n$.

Consider the function of $y=x^3$, then answer for the following questions.

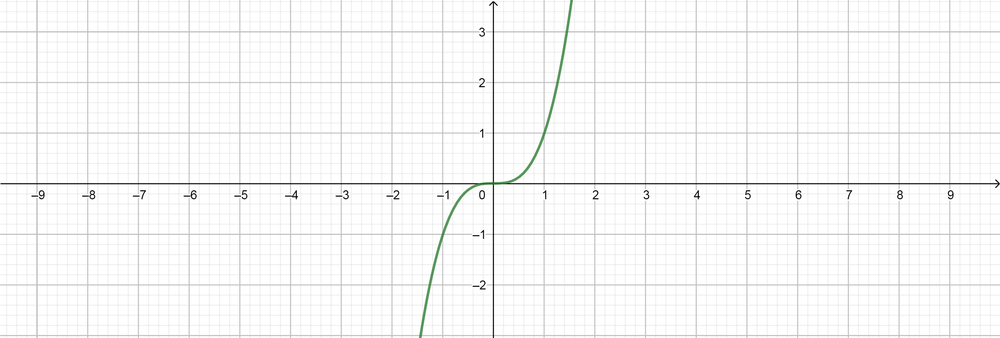
$$
text{color{#4257b2}(a) Use algebraic and graphical example to describe the transformation that could be applied to this function.}
$$

The parent function is a cubic function $y=x^3$, so select some points on the graph to create a new transormed function as follows:

From the graph, the points are, $(-1, -1), (0, 0), (1, 1)$

Assume the transforme values are the following:

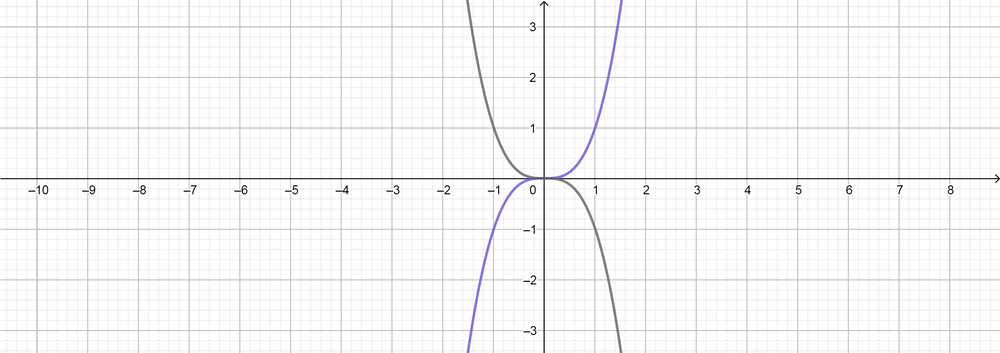
$$
color{#4257b2}(a) a=-1 k=1 d=-2 c=-3
$$

Multiply coordinates of points $(x)$ by $(1)$ and coordinates of points

$(y)$ by $(-1)$, $(x, y) rightarrow (x, -y)$, as follows:

$$
y=x^3 rightarrow y=-x^3
$$

$$
(-1, -1) rightarrow (-1, 1)
$$

$$
(0, 0) rightarrow (0, 0)
$$

$$
(1, 1) rightarrow (1, -1)
$$

Then, add to the coordinates of points $(x)$ by $(-2)$, and coordinates of points

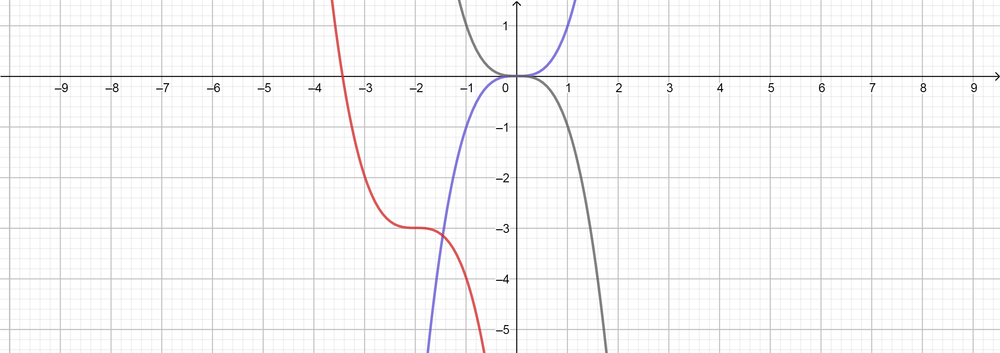
$(y)$ by $(-3)$ $(x, -y) rightarrow (x-2, -y-3)$, as follows:

$$
y=-x^3 rightarrow y=-(x+2)^3-3
$$

$$
(-1, 1) rightarrow (-3, -2)
$$

$$
(0, 0) rightarrow (-2, -3)
$$

$$
(1, -1) rightarrow (-1, -4)
$$

$$
text{color{#4257b2}(b) Exblain why just creating a single table of values is not always the best way to graph the transformed function.}
$$

Because there are some changes can not be calculated in one shot table, so we use two tables to create the transformed function as follows:

First one, study the changes applied to the vertical and horizontal stretch and compressed.

Second one, study the changes that applied to the vertical and horizontal translated.

$$
text{color{Brown}(a) See graphs.
\ \
(b) Because there are some changes cannot be calculated in one shot table, so we use two tables to create the transformed function as follows:
\ \
The first one, study the changes applied to the vertical and horizontal stretch and compressed.
\ \
The second one, study the changes that applied to the vertical and horizontal translated.}
$$

Note that the zeros of a function we obtain by letting $y=0$. Hence for the first function, we obtain:
$$
y=2(x-1)(x+4)(x-5)=0,
$$
which gives the zeros of this function $x=1$, $x=-4$ and $x=5$.

Doing so for the second function, we obtain
$$
y=(x-4)(x+1)(x-8)=0,
$$
and zeros of this function are $x=4$, $x=-1$ and $x=8$.

Note that translating the first function $3$ units to the right, their zeros become $x=1+3=4$, $x=-4+3=-1$ and $x=5+3=8$, same as the second function. Hence, the distances between the zeros are the same, as well as the ratio of these distances between corresponding zeros of the two functions.

Therefore, these two functions have the same general shape and by further stretching and compressing, we can transform on into the other.

$$
text{color{#4257b2}Transform the graph of the function of $y=(x-1)^(x+1)^2$ to determine
\ \
the roots of the function of $y=2(x-1)^2(x+1)^2+1$}
$$

The parent function of $y=(x-1)^(x+1)^2$ transformed by the following terms:

** Vertical stretched by a factor of $(2)$

** Vertical translated by $(1)$ unit up on the vertical axis $(y)$

$$
text{color{Brown}The parent function of $y=(x-1)^(x+1)^2$ transformed by the following terms:
\ \
** Vertical stretched by a factor of $(2)$
\ \
** Vertical translated by $(1)$ unit up on the vertical axis $(y)$}
$$

Find the transformed equation after the first time.

$$
color{#4257b2}a=dfrac{4}{5} k=dfrac{1}{2} c=-6
$$

Standard form is $y=a[k(x-d)]^n+c$

$$
y=dfrac{4}{5}left[dfrac{1}{2} xright]^2-6
$$

$$
text{color{Brown} $y=dfrac{4}{5}left[dfrac{1}{2} xright]^2-6$}
$$