Here we have a $textbf{graph}$ of the boat’s speed versus time:

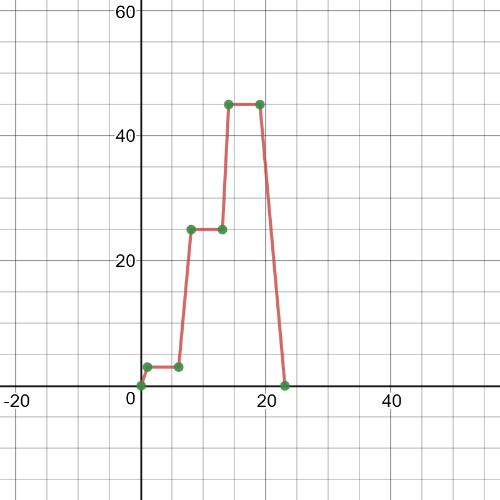
The average rate of change in speed from $t=6$ to $t=8$ is:

$textbf{average rate of change}$ = $dfrac{25-3}{8-6}=11$

The average rate of change in speed from $t=8$ to $t=13$ is:

$textbf{average rate of change}$ = $dfrac{25-25}{13-8}=0$

$textbf{We can conclude that speed is increasing from $t=6$ to $t=8$ and it is constant from $t=8$ to $t=13$.}$

#### (c)

$textbf{Instaneous rate of change is equaivalent to the slope of tangent line in this point}$ because the graph is linear function in this point, so:

$textbf{instaneous rate of change}$ = $11$.

The slope is:

$textbf{slope}$ = $dfrac{25-70}{50-5}=-1$

#### (b)

Slope is negative, that means that temperature is decreasing while time is increasing.

#### (c)

Using linear regression, we get that equation of give function is $f(x)=0.01x^2-1.88x+80.97$, and its derivative is $f'(x)=0.02x-1.88$.So, the slope of the tangent line in point $(30,35)$ is:

$textbf{slope}$ = $f'(30)=-1.28$

#### (d)

Result from part (c) means that temperatue is decreasing at that moment.
#### (e)

In this case, temperature will decrease faster.

Average rate of change over the interval $8leq{x}leq10$ is:

$textbf{average rate of change}$ = $dfrac{P(10)-P(8)}{10-8}=310$
#### (b)

Instaneous rate of change at $x=50$ is:

$textbf{instaneous rate of change}$ = $dfrac{P(50.01)-P(49.99)}{50.01-49.99}=100$
#### (c)

The differnce is that at part (a) we calculated average rate of change over the given period and at part (b) at given moment.

First, we will estimate instaneous rate of change in point $p=-1$ on interval $-1.01leq-1leq-0.99$:

$textbf{instaneous rate of change}$ = $dfrac{h(-0.99)-h(-1.01)}{-0.99+1.01}=-1$

Now, we will estimate instaneous rate of change for $p=-0.75$ on interval $-0.76leq-0.75leq-0.74$:

$textbf{instaneous rate of change}$ = $dfrac{h(-0.74)-h(-0.76)}{-0.74+0.76}=0$

In point $p=1$, we will estimate instaneous rate of change on interval $0.99leq1leq1.01$:

$textbf{instaneous rate of change}$ = $dfrac{h(1.01)-h(0.99)}{1.01-0.99}=7$

Only for point $p=-0.75$ instaneous rate of change is equivalent to $0$, so, in this point might be minimum or maximum. We have next:

$h(-0.75)=-1.125$

$h(-0.74)=h(-0.76)=-1.1248$

We can see that in points after and before point $p=-0.75$ values are greater, so, we can conclude that in this point is $textbf{minimum}$.

First, we will estimate instaneous rate of change in point $x=-2$ on interval $-2.01leq-2leq-1.99$:

$textbf{instaneous rate of change}$ = $dfrac{k(-1.99)-k(-2.01)}{-1.99+2.01}=4.5$

Now, we will estimate instaneous rate of change for $x=4$ on interval $3.99leq4leq4.01$:

$textbf{instaneous rate of change}$ = $dfrac{k(4.01)-k(3.99)}{4.01-3.99}=-4.5$

In point $x=1$, we will estimate instaneous rate of change on interval $0.99leq1leq1.01$:

$textbf{instaneous rate of change}$ = $dfrac{k(1.01)-k(0.99)}{1.01-0.99}=0$

Only for point $x=1$ instaneous rate of change is equivalent to $0$, so, in this point might be minimum or maximum. We have next:

$k(1)=13.75$

$k(0.99)=k(1.01)=13.74999$

We can see that in points after and before point $x=1$ values are smaller, so, we can conclude that in this point is $textbf{maximum}$.